2021-2022学年浙江省温州市南浦实验中学浙教版九年级(下)开学数学试卷 (word版含解析)
文档属性
| 名称 | 2021-2022学年浙江省温州市南浦实验中学浙教版九年级(下)开学数学试卷 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 00:00:00 | ||
图片预览

文档简介
2021-2022学年浙江省温州市南浦实验中学九年级(下)开学数学试卷
一.选择题(本题有10小题,每小题4分,共40分)
1.若=,则的值等于( )
A. B. C. D.
2.下列事件中:
①明天会下雨;
②一个班(40人)里有两人的生日在同一天;
③从装着红球和黑球的袋子里摸出白球;
④太阳东升西落.
不可能事件的个数为( )
A.1 B.2 C.3 D.4
3.将抛物线y=x2的图象向左平移2个单位,所得到的抛物线表达式为( )
A.y=(x+2)2 B.y=(x﹣2)2 C.y=x2+2 D.y=x2﹣2
4.如图,在⊙O中,OC⊥AB于点C,若⊙O的半径为10,OC=5,则弦AB的长为( )
A.5 B.10 C.5 D.10
5.已知⊙O的直径AB与弦AC的夹角为25°,过点C作⊙O的切线交AB的延长线于点D,则∠D等于( )
A.25° B.30° C.35° D.40°
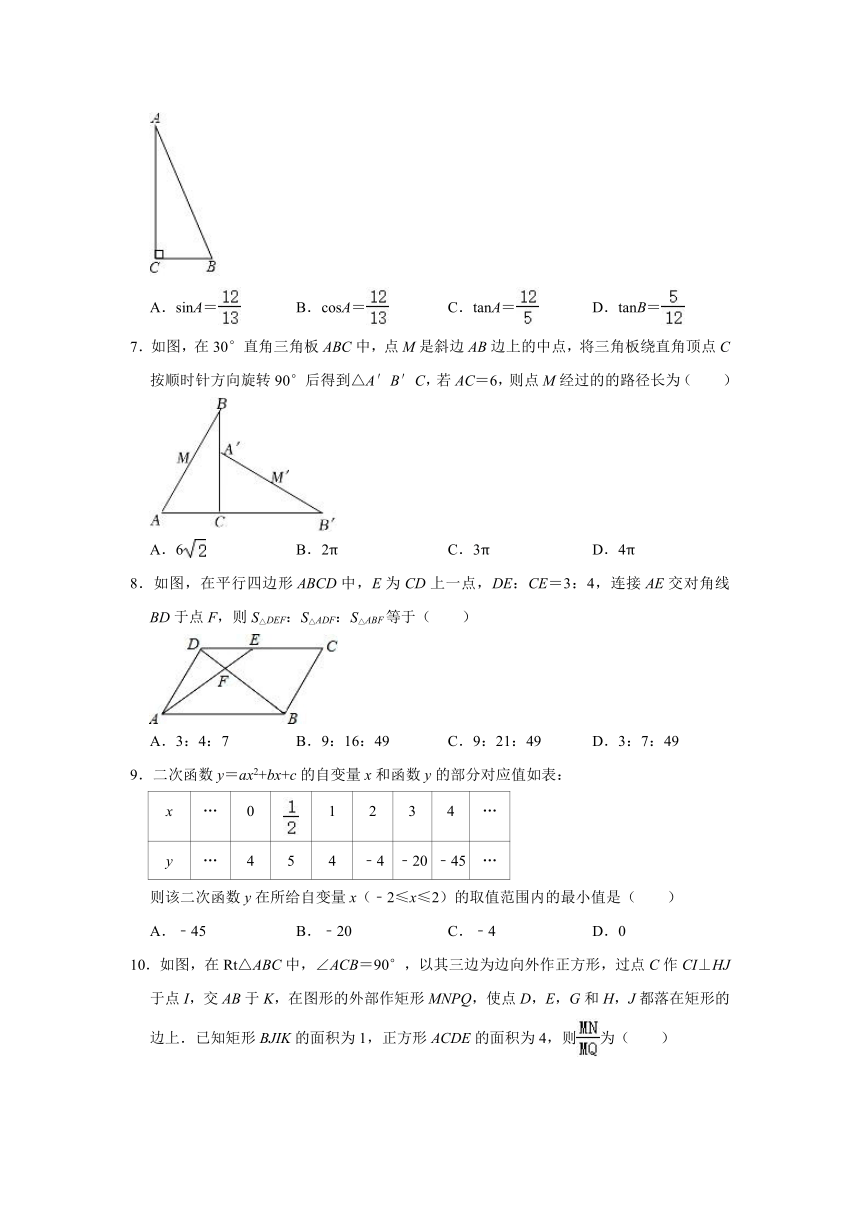
6.如图,在△ABC中,∠C=90°,AB=13,AC=12,下列三角函数表示正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
7.如图,在30°直角三角板ABC中,点M是斜边AB边上的中点,将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,若AC=6,则点M经过的的路径长为( )
A.6 B.2π C.3π D.4π
8.如图,在平行四边形ABCD中,E为CD上一点,DE:CE=3:4,连接AE交对角线BD于点F,则S△DEF:S△ADF:S△ABF等于( )
A.3:4:7 B.9:16:49 C.9:21:49 D.3:7:49
9.二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:
x … 0 1 2 3 4 …
y … 4 5 4 ﹣4 ﹣20 ﹣45 …
则该二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是( )
A.﹣45 B.﹣20 C.﹣4 D.0
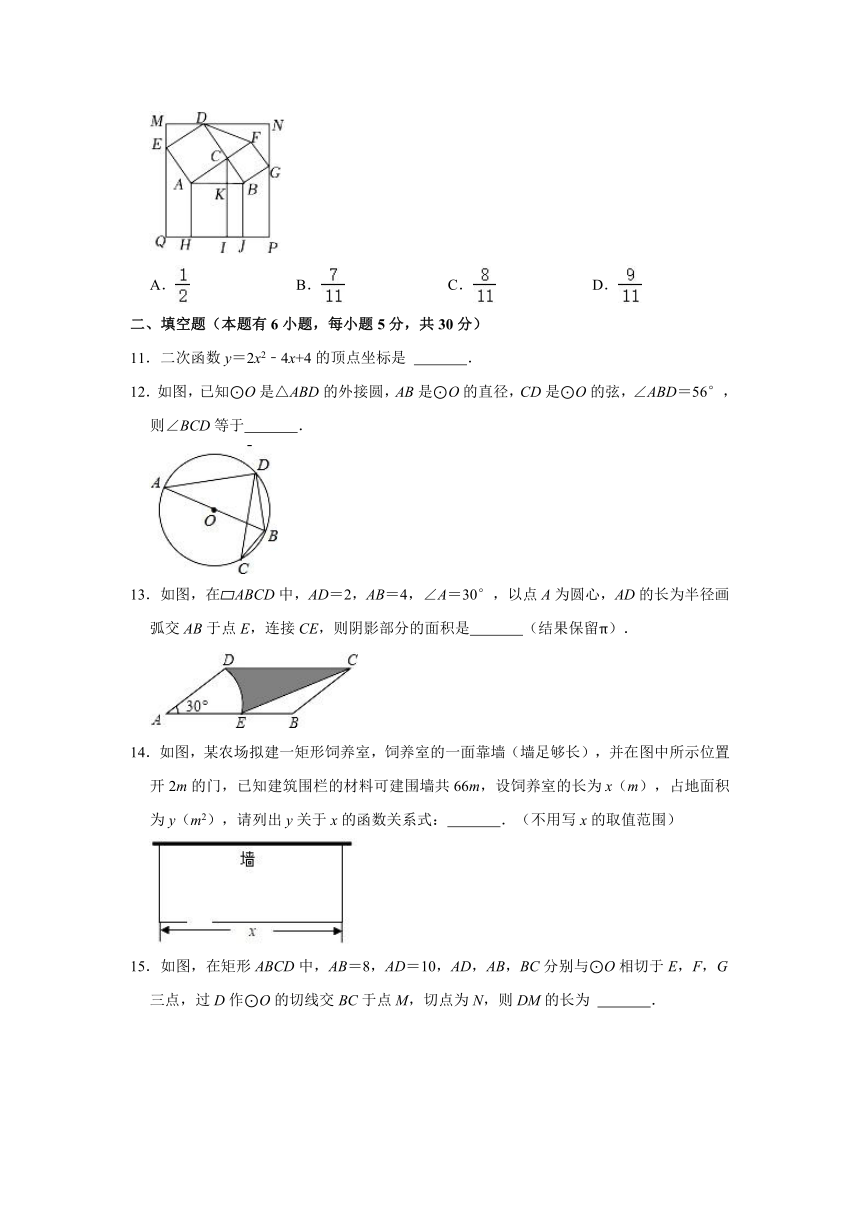
10.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则为( )
A. B. C. D.
二、填空题(本题有6小题,每小题5分,共30分)
11.二次函数y=2x2﹣4x+4的顶点坐标是 .
12.如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD等于 .
13.如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 (结果保留π).
14.如图,某农场拟建一矩形饲养室,饲养室的一面靠墙(墙足够长),并在图中所示位置开2m的门,已知建筑围栏的材料可建围墙共66m,设饲养室的长为x(m),占地面积为y(m2),请列出y关于x的函数关系式: .(不用写x的取值范围)
15.如图,在矩形ABCD中,AB=8,AD=10,AD,AB,BC分别与⊙O相切于E,F,G三点,过D作⊙O的切线交BC于点M,切点为N,则DM的长为 .
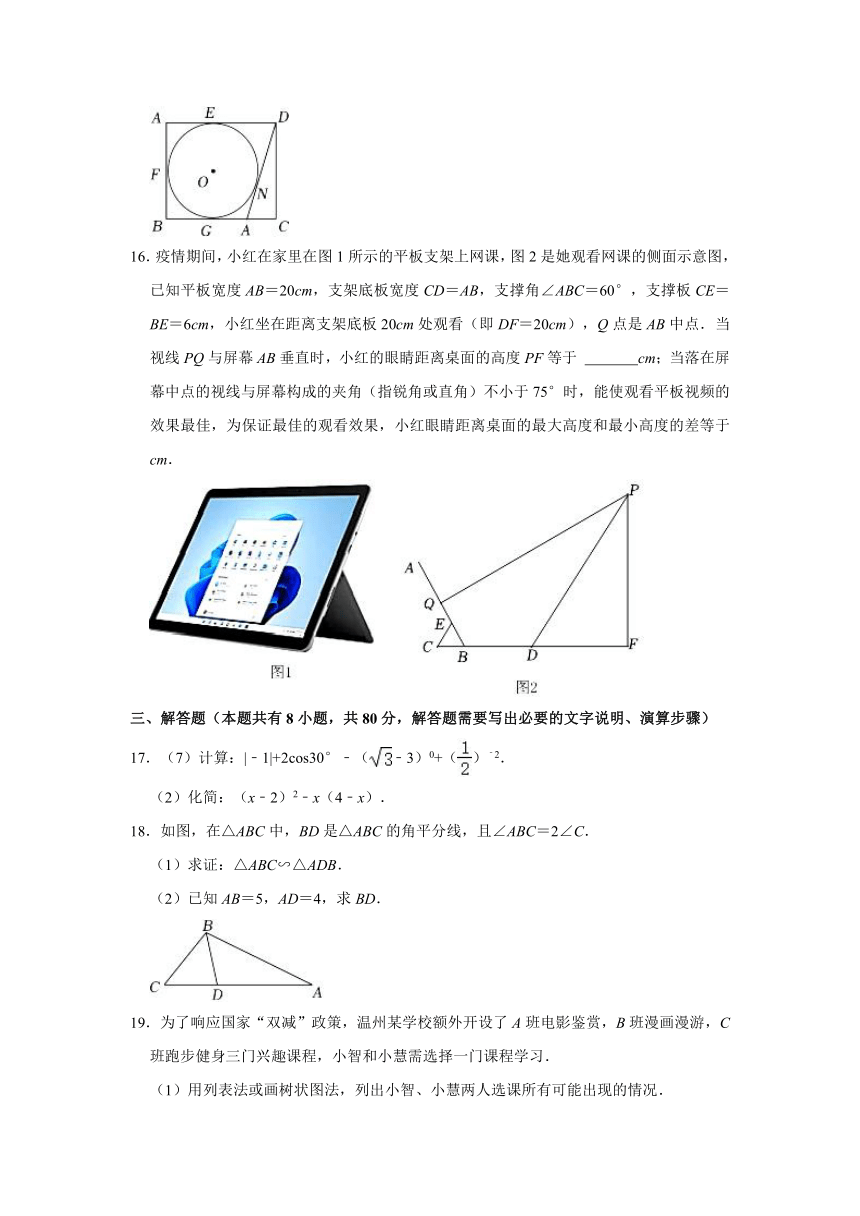
16.疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 cm.
三、解答题(本题共有8小题,共80分,解答题需要写出必要的文字说明、演算步骤)
17.(7)计算:|﹣1|+2cos30°﹣(﹣3)0+()﹣2.
(2)化简:(x﹣2)2﹣x(4﹣x).
18.如图,在△ABC中,BD是△ABC的角平分线,且∠ABC=2∠C.
(1)求证:△ABC∽△ADB.
(2)已知AB=5,AD=4,求BD.
19.为了响应国家“双减”政策,温州某学校额外开设了A班电影鉴赏,B班漫画漫游,C班跑步健身三门兴趣课程,小智和小慧需选择一门课程学习.
(1)用列表法或画树状图法,列出小智、小慧两人选课所有可能出现的情况.
(2)求小智、小慧两人同班的概率.
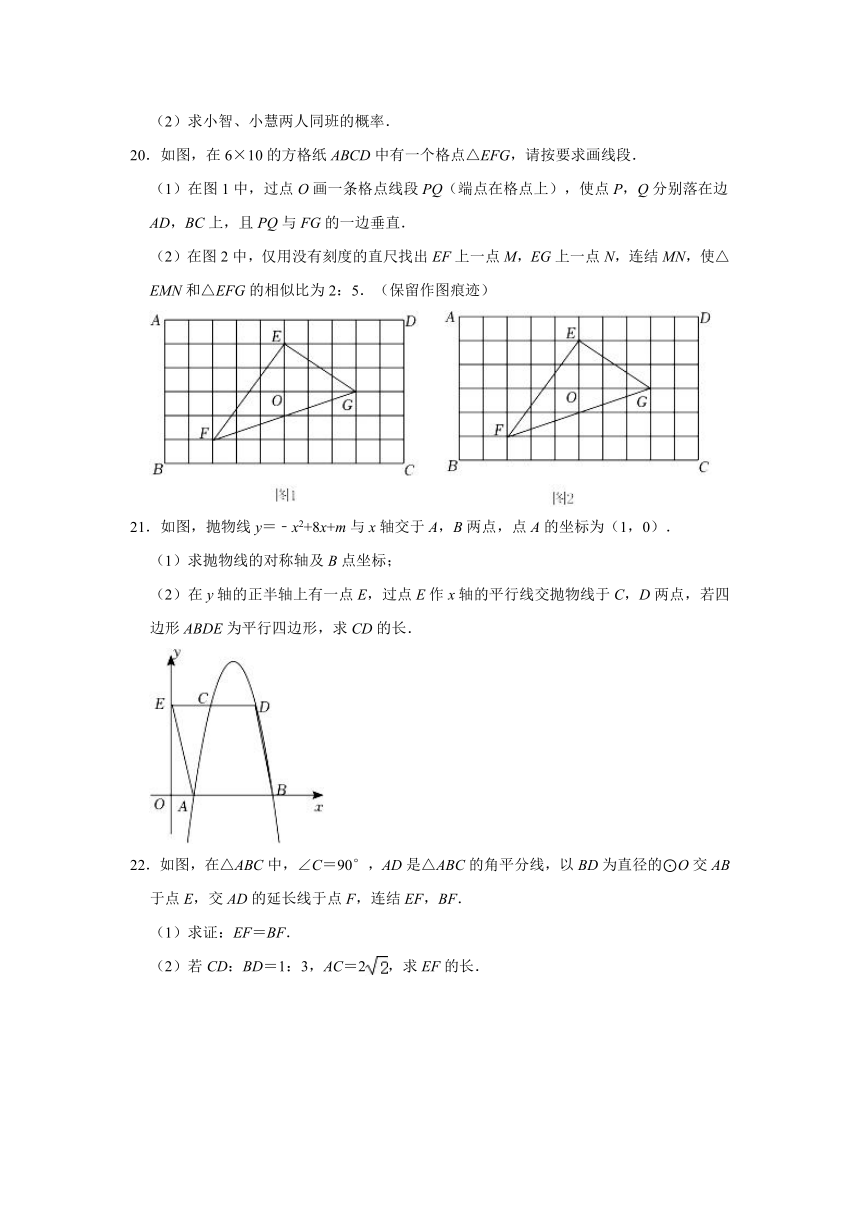
20.如图,在6×10的方格纸ABCD中有一个格点△EFG,请按要求画线段.
(1)在图1中,过点O画一条格点线段PQ(端点在格点上),使点P,Q分别落在边AD,BC上,且PQ与FG的一边垂直.
(2)在图2中,仅用没有刻度的直尺找出EF上一点M,EG上一点N,连结MN,使△EMN和△EFG的相似比为2:5.(保留作图痕迹)
21.如图,抛物线y=﹣x2+8x+m与x轴交于A,B两点,点A的坐标为(1,0).
(1)求抛物线的对称轴及B点坐标;
(2)在y轴的正半轴上有一点E,过点E作x轴的平行线交抛物线于C,D两点,若四边形ABDE为平行四边形,求CD的长.
22.如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,以BD为直径的⊙O交AB于点E,交AD的延长线于点F,连结EF,BF.
(1)求证:EF=BF.
(2)若CD:BD=1:3,AC=2,求EF的长.
23.抗疫期间,全国人民众志成城,温州某商家决定将一个月的利润全部捐给当地医疗机构用于抗疫.该商家购进一批产品,成本10元/件,分为线上和线下两种销售方式.线下市场调查发现,当售价为12元时,月销量1200件,售价每增加1元,月销量减少100件.设月销量y(件),线下售价x(元).(12≤x≤24,且x为整数)
(1)求y关于x的函数关系式;
(2)若线上售价与线下相同,但每件产品商家需多付2元快递费,且线上月销量固定为500件.
①当售价x为多少时,线上和线下的月利润总和最大?并求出最大利润.
②商家第二个月决定继续捐款支持抗疫,捐款方式变为每卖出一件产品就捐款a元,为使商家线上和线下的月利润最低为700元,则a= .(直接写出答案)
24.在菱形ABCD中,对角线AC和BD相交于点O,且AC=16,BD=12.动点P从点A出发以2.5cm/s的速度沿折线A一B一C的路线向终点C运动.过点P作PQ⊥AC,垂足为Q,点Q关于点O的对称点为M,过点P,Q,M作⊙I.设运动时间为t秒.
(1)当t=1时,求AQ和PQ的长.
(2)当P为AB中点时,请判断点B与⊙I的位置关系,并说明理由.
(3)在点P的整个运动过程中.
①当t为何值时,⊙I经过点B.
②当t= 时,⊙I与边AB相切.
参考答案
一.选择题(本题有10小题,每小题4分,共40分。每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.若=,则的值等于( )
A. B. C. D.
【分析】利用设k法进行计算即可解答.
解:∵=,
∴设a=3k,b=4k,
∴===,
故选:C.
2.下列事件中:
①明天会下雨;
②一个班(40人)里有两人的生日在同一天;
③从装着红球和黑球的袋子里摸出白球;
④太阳东升西落.
不可能事件的个数为( )
A.1 B.2 C.3 D.4
【分析】根据随机事件,必然事件,不可能事件的特点判断即可.
解:下列事件中:
①明天会下雨,是随机事件;
②一个班(40人)里有两人的生日在同一天,是随机事件;
③从装着红球和黑球的袋子里摸出白球,是不可能事件;
④太阳东升西落,是必然事件,
不可能事件的个数为:1,
故选:A.
3.将抛物线y=x2的图象向左平移2个单位,所得到的抛物线表达式为( )
A.y=(x+2)2 B.y=(x﹣2)2 C.y=x2+2 D.y=x2﹣2
【分析】根据“左加右减”的规律进行解答即可.
解:将抛物线y=x2的图象向左平移2个单位,所得到的抛物线表达式为:y=(x+2)2,
故选:A.
4.如图,在⊙O中,OC⊥AB于点C,若⊙O的半径为10,OC=5,则弦AB的长为( )
A.5 B.10 C.5 D.10
【分析】连接OA,如图,根据垂径定理得到AC=BC,然后利用勾股定理计算出AC,从而得到AB的长.
解:连接OA,如图,
∵OC⊥AB,
∴AC=BC,
在Rt△OAC中,AC===5,
∴AB=2AC=10.
故选:B.
5.已知⊙O的直径AB与弦AC的夹角为25°,过点C作⊙O的切线交AB的延长线于点D,则∠D等于( )
A.25° B.30° C.35° D.40°
【分析】连接OC,根据切线性质求出∠OCD=90°,根据等腰三角形性质求出∠OCA=∠A=25°,根据三角形外角性质求出∠COD,在△OCD中,根据三角形的内角和定理求出即可.
解:连接OC,
∵OA=OC,∠CAB=25°,
∴∠CAB=∠OCA=25°,
∴∠COD=∠CAB+∠OCA=50°,
∵CD切⊙O于C,
∴∠OCD=90°,
∴∠ADC=180°﹣90°﹣50°=40°,
故选:D.
6.如图,在△ABC中,∠C=90°,AB=13,AC=12,下列三角函数表示正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
【分析】先利用勾股定理可得BC=5,再根据三角函数的定义求解可得.
解:∵∠C=90°,AB=13,AC=12,
∴BC=5,
则sinA==,cosA==,tanA==,tanB==,
故选:B.
7.如图,在30°直角三角板ABC中,点M是斜边AB边上的中点,将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,若AC=6,则点M经过的的路径长为( )
A.6 B.2π C.3π D.4π
【分析】连接CM,CM',根据30°角所对的直角边等于斜边的一半可知AB=2AC=12,再利用CM=AB可得CM的长,由旋转知点M的运动路径为以CM为半径,圆心角为90°的弧,代入弧长公式即可.
解:如图,连接CM,CM',
∵在30°直角三角板ABC中,点M是斜边AB边上的中点,
∴CM=,
∵∠B=30°,
∴AB=2AC=12,
∴CM=6,
由题意知,点M的运动路径为以CM为半径,点C为圆心的弧,
∵将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,
∴∠MCM'=90°,
∴点M经过的的路径长为,
故选:C.
8.如图,在平行四边形ABCD中,E为CD上一点,DE:CE=3:4,连接AE交对角线BD于点F,则S△DEF:S△ADF:S△ABF等于( )
A.3:4:7 B.9:16:49 C.9:21:49 D.3:7:49
【分析】根据平行四边形的性质得到AB=CD,AB∥CD,根据已知条件得到DE:CD=3:7,根据相似三角形的判定和性质即可得到结论.
解:∵四边形ABCD 是平行四边形,
∴AB=CD,AB∥CD,
∵DE:CE=3:4,
∴DE:CD=3:7,
∴DE:AB=3:7,
∵AB∥CD,
∴△DEF∽△BAF,
∴=,
∴S△DEF:S△ADF:=3:7,S△DEF:S△ABF=()2=,
∴S△DEF:S△ADF:S△ABF等于9:21:49,
故选:C.
9.二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:
x … 0 1 2 3 4 …
y … 4 5 4 ﹣4 ﹣20 ﹣45 …
则该二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是( )
A.﹣45 B.﹣20 C.﹣4 D.0
【分析】先由表中数据得到对称轴为直线x=,进而得到函数的增减性,然后求得函数再﹣2≤x≤2时的最小值.
解:由表中数据得到对称轴为直线x=,
∴当x<时,y随x的增大而增大,当x>时,y随x的增大而减小,
∴x=﹣2时,y=﹣20,x=2时,y=﹣4,x=时,y=5,
∴二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是﹣20,
故选:B.
10.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则为( )
A. B. C. D.
【分析】延长AB交PN于点R,延长BA交MQ于点L,连结AG、CJ,设BK=m,先证明△ABG≌△JBC,推导出BC2=S正方形BCFG=S矩形BJIK=1,则BC=1,由AC2=S正方形ACDE=4求得AC=2,再证明△CBK∽△ABC,△ACK∽△ABC,根据相似三角形的对应边成比例推导出CK=2BK=2m,AK=2CK=4m,再证明四边形MNRL、四边形PQLR和四边形AHQL都是矩形,则QL=AH=AB=5m,再证明△DEM≌△EAL≌△ACK,则EM=AL=CK=2m,EL=AK=4m,可求得MQ=11m,再证明△BGR≌△CBK,则BR=CK=2m,可求得MN=9m,即可求得的值为,得到问题的答案.
解:如图,延长AB交PN于点R,延长BA交MQ于点L,连结AG、CJ,设BK=m,
∵四边形BCFG和四边形ABJH都是正方形,四边形BJIK是矩形,
∴BG=BC,BA=BJ,∠CBG=∠ABJ=90°
∴∠ABG=∠JBC=90°+∠ABC,
∴△ABG≌△JBC(SAS),
∴S△ABG=S△JBC,
∵S△ABG=BG BC=S正方形BCFG,S△JBC=BJ BK=S矩形BJIK,
∴S正方形BCFG=S矩形BJIK,
∴BC2=S正方形BCFG=S矩形BJIK=1,
∴BC=1,
∵四边形ACDE是正方形,且AC2=S正方形ACDE=4,
∴AC=2,
∵CI⊥HJ于点I,交AB于K,AB∥HJ,
∴∠CKB=∠CIJ=90°,
∵∠ACB=90°,
∴∠CKB=∠ACB,
∵∠CBK=∠ABC,
∴△CBK∽△ABC,
∴=,
∴==,
∴CK=2BK=2m,
∵∠AKC=∠ACB=90°,∠CAK=∠BAC,
∴△ACK∽△ABC,
∴=,
∴==,
∴AK=2CK=4m,
∵四边形MNPQ和四边形BJIK都是矩形,
∴∠M=∠N=∠P=∠Q=∠PRL=90°,
∴∠LRN=90°,
∴四边形MNRL和四边形PQLR都是矩形,
∴∠ALQ=90°,
∵∠AHJ=90°,
∴∠AHQ=90°,
∴四边形AHQL是矩形,
∴QL=AH=AB=m+4m=5m,
∵∠M=∠ELA=∠AKC=∠AED=∠CAE=90°,
∴∠MED=90°﹣∠AEL=∠LAE=90°﹣∠CAK=∠KCA,
∵DE=EA=AC,
∴△DEM≌△EAL≌△ACK(AAS),
∵EM=AL=CK=2m,EL=AK=4m,
∴MQ=2m+4m+5m=11m,
∵∠BRG=∠CKB=∠CBG=90°,
∴∠BGR=90°﹣∠GBR=∠CBK,
∵BG=BC,
∴△BGR≌△CBK(AAS),
∴BR=CK=2m,
∴MN=LR=2m+5m+2m=9m,
∴==,
故选:D.
二、填空题(本题有6小题,每小题5分,共30分)
11.二次函数y=2x2﹣4x+4的顶点坐标是 (1,2) .
【分析】根据二次函数顶点式解析式写出顶点坐标即可.
解:∵y=2x2﹣4x+4=2(x2﹣2x+2)=2(x﹣1)2+2,
∴二次函数y=2x2﹣4x+4的图象的顶点坐标是(1,2).
故答案为(1,2).
12.如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD等于 34° .
【分析】先根据圆周角定理由AB是⊙O的直径得到∠ADB=90°,再根据互余得到∠A=90°﹣∠ABD=34°,然后根据圆周角定理求解.
解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A=90°﹣∠ABD=90°﹣56°=34°,
∴∠BCD=∠A=34°,
故答案为:34°.
13.如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 3﹣π (结果保留π).
【分析】过D点作DF⊥AB于点F.可求 ABCD和△BCE的高,观察图形可知阴影部分的面积= ABCD的面积﹣扇形ADE的面积﹣△BCE的面积,计算即可求解.
解:过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=30°,
∴DF=AD sin30°=1,EB=AB﹣AE=2,
∴阴影部分的面积:
4×1﹣﹣2×1÷2
=4﹣π﹣1
=3﹣π.
故答案为:3﹣π.
14.如图,某农场拟建一矩形饲养室,饲养室的一面靠墙(墙足够长),并在图中所示位置开2m的门,已知建筑围栏的材料可建围墙共66m,设饲养室的长为x(m),占地面积为y(m2),请列出y关于x的函数关系式: y=﹣x2+34x .(不用写x的取值范围)
【分析】用含x的代数式表示宽,即可得到答案.
解:∵饲养室的长为x(m),
∴饲养室的长用的材料是(x﹣2)m,
∴饲养室的宽是=(34﹣x)m,
∴y=(34﹣x) x=﹣x2+34x,
故答案为:y=﹣x2+34x.
15.如图,在矩形ABCD中,AB=8,AD=10,AD,AB,BC分别与⊙O相切于E,F,G三点,过D作⊙O的切线交BC于点M,切点为N,则DM的长为 .
【分析】连接OE,OF,ON,OG,在矩形ABCD中,得到∠A=∠B=90°,CD=AB=8,由于AD,AB,BC分别与⊙O相切于E,F,G三点,得到∠AEO=∠AFO=∠OFB=∠BGO=90°,推出四边形AFOE,FBGO是正方形,得到AF=BF=AE=BG=4,由勾股定理列方程即可求出结果.
解:连接OE,OF,ON,OG,
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=8,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=4,
∴DE=6,
∵DM是⊙O的切线,
∴DN=DE=6,MN=MG,
∴CM=10﹣4﹣MN=6﹣MN,
在Rt△DMC中,DM2=CD2+CM2,
∴(6+NM)2=(6﹣NM)2+82,
∴NM=,
∴DM=6+=.
故答案为:.
16.疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 18 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 (52﹣78) cm.
【分析】延长PQ交FC延长线于点M,先证明△BCE是等边三角形,进而可以求出PF的值;过点Q作QH⊥BM于点H,求出tan15°==2+,进而可以解决问题.
解:如图,延长PQ交FC延长线于点M,
由题意可知:PM⊥AB,∠ABC=60°,
∴∠QMB=30°,
∵Q点是AB中点.
∴QB=AB=10cm,
∴BM=2QB=20cm,QM=QB=10cm,
∵CE=BE=6cm,∠ABC=60°,
∴△BCE是等边三角形,
∴BC=6cm,
∴BD=CD﹣BC=20﹣6=14cm,
∴FM=BM+BD+DF=20+14+20=54(cm),
∴PF=FM=18(cm),
∴当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于18cm,
∴PM=2PF=36cm,
∴PQ=PM﹣QM=36﹣10=26(cm),
当∠P′QB=75°时,P′F得最小高度,如图,延长P′Q交FC延长线于点N,
∴∠N+∠QBN=∠P′QB,
∴∠N=75°﹣60°=15°,
∵∠QMB=30°,
∴∠MQN=15°,
∴∠MQN=∠N=15°,
∴MQ=MN=10cm,
∴FN=FM+MN=(54+10)cm,
如图,过点Q作QH⊥BM于点H,
设OH=xcm,则QM=MN=2xcm,MH=xcm,
∴NH=MN+MH=(2x+x)cm,
∴tan15°==,
∴tan15°==2+,
∴P′F=(2+)(54+10)=(78﹣34)cm,
∴PP′=PF﹣P′F=18﹣(78﹣34)=(52﹣78)cm.
故答案为:18;(52﹣78)cm.
三、解答题(本题共有8小题,共80分,解答题需要写出必要的文字说明、演算步骤)
17.(7)计算:|﹣1|+2cos30°﹣(﹣3)0+()﹣2.
(2)化简:(x﹣2)2﹣x(4﹣x).
【分析】(1)利用绝对值的意义,特殊角的三角函数值,零指数幂的意义和负整数指数幂的意义解答即可;
(2)先利用完全平方公式和单项式乘以多项式的法则去掉括号,再合并同类项即可.
解:(1)原式=1+2×﹣1+4
=1+﹣1+4
=4+;
(2)原式=x2﹣4x+4﹣4x+x2
=2x2﹣8x+4.
18.如图,在△ABC中,BD是△ABC的角平分线,且∠ABC=2∠C.
(1)求证:△ABC∽△ADB.
(2)已知AB=5,AD=4,求BD.
【分析】(1)由BD是△ABC的角平分线得∠ABD=∠DBC=∠ABC,则∠ABC=2∠C得∠C=∠ABC,所以∠C=∠ABD,而∠A是△ABC和△ADB的公共角,则根据“有两个角分别相等的两个三角形相似”可以证明△ABC∽△ADB;
(2)由△ABC∽△ADB得=,其中AB=5,AD=4,可以求出AC的长,再求出CD的长,由∠DBC=∠ABC,∠C=∠ABC,得∠DBC=∠C,则BD=CD,可以求出BD的长.
【解答】(1)证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBC=∠ABC,
∵∠ABC=2∠C,
∴∠C=∠ABC,
∴∠C=∠ABD,
∵∠A=∠A,
∴△ABC∽△ADB.
(2)解:∵△ABC∽△ADB,
∴=,
∵AB=5,AD=4,
∴AC===,
∴CD=AC﹣AD=﹣4=,
∵∠DBC=∠ABC,∠C=∠ABC,
∴∠DBC=∠C,
∴BD=CD=,
∴BD的长为.
19.为了响应国家“双减”政策,温州某学校额外开设了A班电影鉴赏,B班漫画漫游,C班跑步健身三门兴趣课程,小智和小慧需选择一门课程学习.
(1)用列表法或画树状图法,列出小智、小慧两人选课所有可能出现的情况.
(2)求小智、小慧两人同班的概率.
【分析】(1))根据题意画出树状图,即可得出所有等可能的情况数;
(2)由(1)可知,共有9种等可能的结果,其中小智、小慧两人同班的结果有1种,再由概率公式求解即可.
解:(1)根据题意画树状图如下:
则小智、小慧两人选课所有可能出现的情况共有9种;
(2)∵共有9种等可能的情况数,其中小智、小慧两人同班的有3种,
∴小智、小慧两人同班的概率是=.
20.如图,在6×10的方格纸ABCD中有一个格点△EFG,请按要求画线段.
(1)在图1中,过点O画一条格点线段PQ(端点在格点上),使点P,Q分别落在边AD,BC上,且PQ与FG的一边垂直.
(2)在图2中,仅用没有刻度的直尺找出EF上一点M,EG上一点N,连结MN,使△EMN和△EFG的相似比为2:5.(保留作图痕迹)
【分析】(1)利用数形结合的思想画出图形即可;
(2)取格点J,K,连接OJ交EF于点M,连接OK交EG于点N,连接MN即可.
解:(1)如图1中,线段PQ即为所求;
(2)如图2中,线段MN即为所求.
21.如图,抛物线y=﹣x2+8x+m与x轴交于A,B两点,点A的坐标为(1,0).
(1)求抛物线的对称轴及B点坐标;
(2)在y轴的正半轴上有一点E,过点E作x轴的平行线交抛物线于C,D两点,若四边形ABDE为平行四边形,求CD的长.
【分析】(1)把A(1,0)代入y=﹣x2+8x+m,列方程求出m的值为﹣7,则抛物线的解析式为y=﹣x2+8x﹣7,将y=﹣x2+8x﹣7配成顶点式,得到抛物线的对称轴为直线x=4,令y=0,则﹣x2+8x﹣7=0,解方程求出x的值,即得到点B的坐标为(7,0);
(2)作抛物线的对称轴交DE于点F,则点F的横坐标为4,由四边形ABDE为平行四边形,得DE=AB=6,则DF=6﹣4=2,由抛物线的对称性得CF=DF=2,即可求得CD=4.
解:(1)把A(1,0)代入y=﹣x2+8x+m,得﹣1+8+m=0,
解得m=﹣7,
∴抛物线的解析式为y=﹣x2+8x﹣7,
∵y=﹣x2+8x﹣7=﹣(x﹣4)2+9,
∴抛物线的对称轴为直线x=4;
当y=0时,则﹣x2+8x﹣7=0,
解得x1=1,x2=7,
B(7,0).
(2)如图,作抛物线的对称轴交DE于点F,则点F的横坐标为4,
∴EF=4,
∵四边形ABDE为平行四边形,
∴DE=AB=7﹣1=6,
∴CF=DF=6﹣4=2,
∴CD=CF+DF=2+2=4,
∴CD的长为4.
22.如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,以BD为直径的⊙O交AB于点E,交AD的延长线于点F,连结EF,BF.
(1)求证:EF=BF.
(2)若CD:BD=1:3,AC=2,求EF的长.
【分析】(1)先利用圆周角定理得到∠DBF=∠DEB=90°,∠5=∠6,再证明∠4=∠ABF,从而得到∠6=∠ABF,所以EF=BF;
(2)先根据角平分线的性质得到DE=DC,则DE:BD=1:3,接着证明△BDE∽△BAC,利用相似比和比例的性质得到AB=3AC=6,则根据勾股定理可计算出BC=8,于是得到CD=2,AD=2,然后证明△ACD∽△AFB,利用相似比可计算出BF=2,从而得到EF的长.
【解答】(1)证明:连接DE,如图,
∵BD为直径,
∴∠DBF=∠DEB=90°,
∵AD是△ABC的角平分线,
∴∠1=∠2,
∵∠1+∠4=90°,∠2+∠ABF=90°,
∴∠4=∠ABF,
∵∠4=∠5,∠5=∠6,
∴∠6=∠ABF,
∴EF=BF;
(2)解:∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴DE=DC,
∵CD:BD=1:3,
∴DE:BD=1:3,
∵∠DEB=∠C,∠DBE=∠ABC,
∴△BDE∽△BAC,
∴=,
∴==3,
∴AB=3AC=3×2=6,
∴BC===8,
∴CD=BC=2,
∴AD==2,
∵∠1=∠2,∠C=∠AFB,
∴△ACD∽△AFB,
∴=,即=,
∴BF=2,
∴EF=2.
23.抗疫期间,全国人民众志成城,温州某商家决定将一个月的利润全部捐给当地医疗机构用于抗疫.该商家购进一批产品,成本10元/件,分为线上和线下两种销售方式.线下市场调查发现,当售价为12元时,月销量1200件,售价每增加1元,月销量减少100件.设月销量y(件),线下售价x(元).(12≤x≤24,且x为整数)
(1)求y关于x的函数关系式;
(2)若线上售价与线下相同,但每件产品商家需多付2元快递费,且线上月销量固定为500件.
①当售价x为多少时,线上和线下的月利润总和最大?并求出最大利润.
②商家第二个月决定继续捐款支持抗疫,捐款方式变为每卖出一件产品就捐款a元,为使商家线上和线下的月利润最低为700元,则a= 1 .(直接写出答案)
【分析】(1)根据月销量=1200﹣月销量减小件数求解.
(2)①根据月利润总和=线上利润+线下利润列出利润总和与x的关系,解析式化为顶点式求解.
②分类讨论x=12和x=24时商家月利润为700时求出a的值.
解:(1)根据题意得:y=1200﹣100(x﹣12)=﹣100x+2400,
∴y关于x的函数关系式为y=﹣100x+2400;
(2)①设线上和线下的月利润总和为w元,则
w=500(x﹣10﹣2)+y(x﹣10)
=500x﹣6000+(﹣100x+2400)(x﹣10)
=﹣100x2+3900x﹣30000,
=﹣100(x﹣)2+8025,
∵﹣100<0,12≤x≤24,且x为整数,
∴当x=19或20时,w有最大值,最大值为8000,
∴当x为19或20时,线上和线下的月利润总和达到最大,最大利润为8000元;
②设商家线上和线下的月利润总和为w元,
根据题意得,w=500(x﹣2﹣10﹣a)+(x﹣10﹣a)(﹣100x+2400),
即w=﹣100x2+(3900+100a)x﹣30000﹣2900a,
∵﹣100<0,抛物线开口向下,
∴x==,
当x=12,w取最小值为700时,700=﹣100×122+12×3900+12×100a﹣30000﹣2900a,
解得a=1,
此时抛物线对称轴为直线x==20,
20﹣12>24﹣20,满足题意.
当x=24,w取最小值为700时,700=﹣100×242+3900×24+24×100a﹣30000﹣2900a,
解得a=10.6,
此时抛物线对称轴为直线x==24.8,
24.8﹣24>24.8﹣12,不满足题意.
故答案为:1.
24.在菱形ABCD中,对角线AC和BD相交于点O,且AC=16,BD=12.动点P从点A出发以2.5cm/s的速度沿折线A一B一C的路线向终点C运动.过点P作PQ⊥AC,垂足为Q,点Q关于点O的对称点为M,过点P,Q,M作⊙I.设运动时间为t秒.
(1)当t=1时,求AQ和PQ的长.
(2)当P为AB中点时,请判断点B与⊙I的位置关系,并说明理由.
(3)在点P的整个运动过程中.
①当t为何值时,⊙I经过点B.
②当t= 4或 时,⊙I与边AB相切.
【分析】(1)利用菱形的性质及勾股定理求出OA、OB、AB的长度,根据题意求出AP的长度,再利用相似三角形的判断与性质即可求出AQ和PQ的长度;
(2)利用菱形的性质、对称的性质求出⊙I的半径和IB的长度,通过比较即可判断出点B与⊙I的位置关系;
(3)①根据题意先表示出OQ和OI的长度,进而表示出半径r,求出BI的长度,利用BI=r,列出方程,解方程即可求出t的值;
②⊙I与AB相切,则与AC也相切,对出切点为P,求出BP的长,表示出r,由①得出r,进而得出方程,解方程即可得出t的值.
解:(1)如图1,
∵四边形ABCD是菱形,AC=16,BD=12,
∴AC⊥BD,AO=AC=×16=8,BO=BD=×12=6,
∴AB===10,
∵PQ⊥AC,
∴∠AQP=∠AOB=90°,
∵∠QAP=∠OAB,
∴△AQP∽△AOB,
∴,
当t=1时,AP=2.5×1=2.5,
∴,,
∴AQ=2,PQ=1.5;
(2)如图2,
点B在⊙I外,理由如下:
连接PM交OB与点I,
当P为AB中点时,
OQ=AO=×8=4,PQ=BO=×6=3,
∵点Q关于点O的对称点为M,
∴QM=2OA=2×4=8,
∵PQ⊥OA,
∴PM为⊙I的直径,I为圆心,PM===,
∴⊙I的半径r=,
∵O是QM的中点,I是PM的中点,
∴OI是△MQP的中位线,
∴OI=PQ=×3=,
∴IB=OB﹣OI=6﹣=>r,
∴点B在⊙I外.
(3)①∵OQ=AO﹣AQ=AO﹣,
OI=,
∴r=,
BI=OB﹣OI=6﹣,
若⊙I经过点B,则BI=r,
∴BI2=r2,
∴t2﹣32t+64=(6﹣t)2,
∴4t2﹣23t+28=0,
解得:t=4或t=,
∴当t为4或时,⊙I经过点B;
②r=,
∵⊙I与AB相切,
∴⊙I与AC也相切,与AB的切点为P,则BP=AB﹣AP=10﹣2.5t,
∵r=,
∴,
∴,
解得:t=4或t=,
∴当t=4或t=时,⊙I与边AB相切,
故答案为:4或.
一.选择题(本题有10小题,每小题4分,共40分)
1.若=,则的值等于( )
A. B. C. D.
2.下列事件中:
①明天会下雨;
②一个班(40人)里有两人的生日在同一天;
③从装着红球和黑球的袋子里摸出白球;
④太阳东升西落.
不可能事件的个数为( )
A.1 B.2 C.3 D.4
3.将抛物线y=x2的图象向左平移2个单位,所得到的抛物线表达式为( )
A.y=(x+2)2 B.y=(x﹣2)2 C.y=x2+2 D.y=x2﹣2
4.如图,在⊙O中,OC⊥AB于点C,若⊙O的半径为10,OC=5,则弦AB的长为( )
A.5 B.10 C.5 D.10
5.已知⊙O的直径AB与弦AC的夹角为25°,过点C作⊙O的切线交AB的延长线于点D,则∠D等于( )
A.25° B.30° C.35° D.40°
6.如图,在△ABC中,∠C=90°,AB=13,AC=12,下列三角函数表示正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
7.如图,在30°直角三角板ABC中,点M是斜边AB边上的中点,将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,若AC=6,则点M经过的的路径长为( )
A.6 B.2π C.3π D.4π
8.如图,在平行四边形ABCD中,E为CD上一点,DE:CE=3:4,连接AE交对角线BD于点F,则S△DEF:S△ADF:S△ABF等于( )
A.3:4:7 B.9:16:49 C.9:21:49 D.3:7:49
9.二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:
x … 0 1 2 3 4 …
y … 4 5 4 ﹣4 ﹣20 ﹣45 …
则该二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是( )
A.﹣45 B.﹣20 C.﹣4 D.0
10.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则为( )
A. B. C. D.
二、填空题(本题有6小题,每小题5分,共30分)
11.二次函数y=2x2﹣4x+4的顶点坐标是 .
12.如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD等于 .
13.如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 (结果保留π).
14.如图,某农场拟建一矩形饲养室,饲养室的一面靠墙(墙足够长),并在图中所示位置开2m的门,已知建筑围栏的材料可建围墙共66m,设饲养室的长为x(m),占地面积为y(m2),请列出y关于x的函数关系式: .(不用写x的取值范围)
15.如图,在矩形ABCD中,AB=8,AD=10,AD,AB,BC分别与⊙O相切于E,F,G三点,过D作⊙O的切线交BC于点M,切点为N,则DM的长为 .
16.疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 cm.
三、解答题(本题共有8小题,共80分,解答题需要写出必要的文字说明、演算步骤)
17.(7)计算:|﹣1|+2cos30°﹣(﹣3)0+()﹣2.
(2)化简:(x﹣2)2﹣x(4﹣x).
18.如图,在△ABC中,BD是△ABC的角平分线,且∠ABC=2∠C.
(1)求证:△ABC∽△ADB.
(2)已知AB=5,AD=4,求BD.
19.为了响应国家“双减”政策,温州某学校额外开设了A班电影鉴赏,B班漫画漫游,C班跑步健身三门兴趣课程,小智和小慧需选择一门课程学习.
(1)用列表法或画树状图法,列出小智、小慧两人选课所有可能出现的情况.
(2)求小智、小慧两人同班的概率.
20.如图,在6×10的方格纸ABCD中有一个格点△EFG,请按要求画线段.
(1)在图1中,过点O画一条格点线段PQ(端点在格点上),使点P,Q分别落在边AD,BC上,且PQ与FG的一边垂直.
(2)在图2中,仅用没有刻度的直尺找出EF上一点M,EG上一点N,连结MN,使△EMN和△EFG的相似比为2:5.(保留作图痕迹)
21.如图,抛物线y=﹣x2+8x+m与x轴交于A,B两点,点A的坐标为(1,0).
(1)求抛物线的对称轴及B点坐标;
(2)在y轴的正半轴上有一点E,过点E作x轴的平行线交抛物线于C,D两点,若四边形ABDE为平行四边形,求CD的长.
22.如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,以BD为直径的⊙O交AB于点E,交AD的延长线于点F,连结EF,BF.
(1)求证:EF=BF.
(2)若CD:BD=1:3,AC=2,求EF的长.
23.抗疫期间,全国人民众志成城,温州某商家决定将一个月的利润全部捐给当地医疗机构用于抗疫.该商家购进一批产品,成本10元/件,分为线上和线下两种销售方式.线下市场调查发现,当售价为12元时,月销量1200件,售价每增加1元,月销量减少100件.设月销量y(件),线下售价x(元).(12≤x≤24,且x为整数)
(1)求y关于x的函数关系式;
(2)若线上售价与线下相同,但每件产品商家需多付2元快递费,且线上月销量固定为500件.
①当售价x为多少时,线上和线下的月利润总和最大?并求出最大利润.
②商家第二个月决定继续捐款支持抗疫,捐款方式变为每卖出一件产品就捐款a元,为使商家线上和线下的月利润最低为700元,则a= .(直接写出答案)
24.在菱形ABCD中,对角线AC和BD相交于点O,且AC=16,BD=12.动点P从点A出发以2.5cm/s的速度沿折线A一B一C的路线向终点C运动.过点P作PQ⊥AC,垂足为Q,点Q关于点O的对称点为M,过点P,Q,M作⊙I.设运动时间为t秒.
(1)当t=1时,求AQ和PQ的长.
(2)当P为AB中点时,请判断点B与⊙I的位置关系,并说明理由.
(3)在点P的整个运动过程中.
①当t为何值时,⊙I经过点B.
②当t= 时,⊙I与边AB相切.
参考答案
一.选择题(本题有10小题,每小题4分,共40分。每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.若=,则的值等于( )
A. B. C. D.
【分析】利用设k法进行计算即可解答.
解:∵=,
∴设a=3k,b=4k,
∴===,
故选:C.
2.下列事件中:
①明天会下雨;
②一个班(40人)里有两人的生日在同一天;
③从装着红球和黑球的袋子里摸出白球;
④太阳东升西落.
不可能事件的个数为( )
A.1 B.2 C.3 D.4
【分析】根据随机事件,必然事件,不可能事件的特点判断即可.
解:下列事件中:
①明天会下雨,是随机事件;
②一个班(40人)里有两人的生日在同一天,是随机事件;
③从装着红球和黑球的袋子里摸出白球,是不可能事件;
④太阳东升西落,是必然事件,
不可能事件的个数为:1,
故选:A.
3.将抛物线y=x2的图象向左平移2个单位,所得到的抛物线表达式为( )
A.y=(x+2)2 B.y=(x﹣2)2 C.y=x2+2 D.y=x2﹣2
【分析】根据“左加右减”的规律进行解答即可.
解:将抛物线y=x2的图象向左平移2个单位,所得到的抛物线表达式为:y=(x+2)2,
故选:A.
4.如图,在⊙O中,OC⊥AB于点C,若⊙O的半径为10,OC=5,则弦AB的长为( )
A.5 B.10 C.5 D.10
【分析】连接OA,如图,根据垂径定理得到AC=BC,然后利用勾股定理计算出AC,从而得到AB的长.
解:连接OA,如图,
∵OC⊥AB,
∴AC=BC,
在Rt△OAC中,AC===5,
∴AB=2AC=10.
故选:B.
5.已知⊙O的直径AB与弦AC的夹角为25°,过点C作⊙O的切线交AB的延长线于点D,则∠D等于( )
A.25° B.30° C.35° D.40°
【分析】连接OC,根据切线性质求出∠OCD=90°,根据等腰三角形性质求出∠OCA=∠A=25°,根据三角形外角性质求出∠COD,在△OCD中,根据三角形的内角和定理求出即可.
解:连接OC,
∵OA=OC,∠CAB=25°,
∴∠CAB=∠OCA=25°,
∴∠COD=∠CAB+∠OCA=50°,
∵CD切⊙O于C,
∴∠OCD=90°,
∴∠ADC=180°﹣90°﹣50°=40°,
故选:D.
6.如图,在△ABC中,∠C=90°,AB=13,AC=12,下列三角函数表示正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
【分析】先利用勾股定理可得BC=5,再根据三角函数的定义求解可得.
解:∵∠C=90°,AB=13,AC=12,
∴BC=5,
则sinA==,cosA==,tanA==,tanB==,
故选:B.
7.如图,在30°直角三角板ABC中,点M是斜边AB边上的中点,将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,若AC=6,则点M经过的的路径长为( )
A.6 B.2π C.3π D.4π
【分析】连接CM,CM',根据30°角所对的直角边等于斜边的一半可知AB=2AC=12,再利用CM=AB可得CM的长,由旋转知点M的运动路径为以CM为半径,圆心角为90°的弧,代入弧长公式即可.
解:如图,连接CM,CM',
∵在30°直角三角板ABC中,点M是斜边AB边上的中点,
∴CM=,
∵∠B=30°,
∴AB=2AC=12,
∴CM=6,
由题意知,点M的运动路径为以CM为半径,点C为圆心的弧,
∵将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,
∴∠MCM'=90°,
∴点M经过的的路径长为,
故选:C.
8.如图,在平行四边形ABCD中,E为CD上一点,DE:CE=3:4,连接AE交对角线BD于点F,则S△DEF:S△ADF:S△ABF等于( )
A.3:4:7 B.9:16:49 C.9:21:49 D.3:7:49
【分析】根据平行四边形的性质得到AB=CD,AB∥CD,根据已知条件得到DE:CD=3:7,根据相似三角形的判定和性质即可得到结论.
解:∵四边形ABCD 是平行四边形,
∴AB=CD,AB∥CD,
∵DE:CE=3:4,
∴DE:CD=3:7,
∴DE:AB=3:7,
∵AB∥CD,
∴△DEF∽△BAF,
∴=,
∴S△DEF:S△ADF:=3:7,S△DEF:S△ABF=()2=,
∴S△DEF:S△ADF:S△ABF等于9:21:49,
故选:C.
9.二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:
x … 0 1 2 3 4 …
y … 4 5 4 ﹣4 ﹣20 ﹣45 …
则该二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是( )
A.﹣45 B.﹣20 C.﹣4 D.0
【分析】先由表中数据得到对称轴为直线x=,进而得到函数的增减性,然后求得函数再﹣2≤x≤2时的最小值.
解:由表中数据得到对称轴为直线x=,
∴当x<时,y随x的增大而增大,当x>时,y随x的增大而减小,
∴x=﹣2时,y=﹣20,x=2时,y=﹣4,x=时,y=5,
∴二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是﹣20,
故选:B.
10.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则为( )
A. B. C. D.
【分析】延长AB交PN于点R,延长BA交MQ于点L,连结AG、CJ,设BK=m,先证明△ABG≌△JBC,推导出BC2=S正方形BCFG=S矩形BJIK=1,则BC=1,由AC2=S正方形ACDE=4求得AC=2,再证明△CBK∽△ABC,△ACK∽△ABC,根据相似三角形的对应边成比例推导出CK=2BK=2m,AK=2CK=4m,再证明四边形MNRL、四边形PQLR和四边形AHQL都是矩形,则QL=AH=AB=5m,再证明△DEM≌△EAL≌△ACK,则EM=AL=CK=2m,EL=AK=4m,可求得MQ=11m,再证明△BGR≌△CBK,则BR=CK=2m,可求得MN=9m,即可求得的值为,得到问题的答案.
解:如图,延长AB交PN于点R,延长BA交MQ于点L,连结AG、CJ,设BK=m,
∵四边形BCFG和四边形ABJH都是正方形,四边形BJIK是矩形,
∴BG=BC,BA=BJ,∠CBG=∠ABJ=90°
∴∠ABG=∠JBC=90°+∠ABC,
∴△ABG≌△JBC(SAS),
∴S△ABG=S△JBC,
∵S△ABG=BG BC=S正方形BCFG,S△JBC=BJ BK=S矩形BJIK,
∴S正方形BCFG=S矩形BJIK,
∴BC2=S正方形BCFG=S矩形BJIK=1,
∴BC=1,
∵四边形ACDE是正方形,且AC2=S正方形ACDE=4,
∴AC=2,
∵CI⊥HJ于点I,交AB于K,AB∥HJ,
∴∠CKB=∠CIJ=90°,
∵∠ACB=90°,
∴∠CKB=∠ACB,
∵∠CBK=∠ABC,
∴△CBK∽△ABC,
∴=,
∴==,
∴CK=2BK=2m,
∵∠AKC=∠ACB=90°,∠CAK=∠BAC,
∴△ACK∽△ABC,
∴=,
∴==,
∴AK=2CK=4m,
∵四边形MNPQ和四边形BJIK都是矩形,
∴∠M=∠N=∠P=∠Q=∠PRL=90°,
∴∠LRN=90°,
∴四边形MNRL和四边形PQLR都是矩形,
∴∠ALQ=90°,
∵∠AHJ=90°,
∴∠AHQ=90°,
∴四边形AHQL是矩形,
∴QL=AH=AB=m+4m=5m,
∵∠M=∠ELA=∠AKC=∠AED=∠CAE=90°,
∴∠MED=90°﹣∠AEL=∠LAE=90°﹣∠CAK=∠KCA,
∵DE=EA=AC,
∴△DEM≌△EAL≌△ACK(AAS),
∵EM=AL=CK=2m,EL=AK=4m,
∴MQ=2m+4m+5m=11m,
∵∠BRG=∠CKB=∠CBG=90°,
∴∠BGR=90°﹣∠GBR=∠CBK,
∵BG=BC,
∴△BGR≌△CBK(AAS),
∴BR=CK=2m,
∴MN=LR=2m+5m+2m=9m,
∴==,
故选:D.
二、填空题(本题有6小题,每小题5分,共30分)
11.二次函数y=2x2﹣4x+4的顶点坐标是 (1,2) .
【分析】根据二次函数顶点式解析式写出顶点坐标即可.
解:∵y=2x2﹣4x+4=2(x2﹣2x+2)=2(x﹣1)2+2,
∴二次函数y=2x2﹣4x+4的图象的顶点坐标是(1,2).
故答案为(1,2).
12.如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD等于 34° .
【分析】先根据圆周角定理由AB是⊙O的直径得到∠ADB=90°,再根据互余得到∠A=90°﹣∠ABD=34°,然后根据圆周角定理求解.
解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A=90°﹣∠ABD=90°﹣56°=34°,
∴∠BCD=∠A=34°,
故答案为:34°.
13.如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 3﹣π (结果保留π).
【分析】过D点作DF⊥AB于点F.可求 ABCD和△BCE的高,观察图形可知阴影部分的面积= ABCD的面积﹣扇形ADE的面积﹣△BCE的面积,计算即可求解.
解:过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=30°,
∴DF=AD sin30°=1,EB=AB﹣AE=2,
∴阴影部分的面积:
4×1﹣﹣2×1÷2
=4﹣π﹣1
=3﹣π.
故答案为:3﹣π.
14.如图,某农场拟建一矩形饲养室,饲养室的一面靠墙(墙足够长),并在图中所示位置开2m的门,已知建筑围栏的材料可建围墙共66m,设饲养室的长为x(m),占地面积为y(m2),请列出y关于x的函数关系式: y=﹣x2+34x .(不用写x的取值范围)
【分析】用含x的代数式表示宽,即可得到答案.
解:∵饲养室的长为x(m),
∴饲养室的长用的材料是(x﹣2)m,
∴饲养室的宽是=(34﹣x)m,
∴y=(34﹣x) x=﹣x2+34x,
故答案为:y=﹣x2+34x.
15.如图,在矩形ABCD中,AB=8,AD=10,AD,AB,BC分别与⊙O相切于E,F,G三点,过D作⊙O的切线交BC于点M,切点为N,则DM的长为 .
【分析】连接OE,OF,ON,OG,在矩形ABCD中,得到∠A=∠B=90°,CD=AB=8,由于AD,AB,BC分别与⊙O相切于E,F,G三点,得到∠AEO=∠AFO=∠OFB=∠BGO=90°,推出四边形AFOE,FBGO是正方形,得到AF=BF=AE=BG=4,由勾股定理列方程即可求出结果.
解:连接OE,OF,ON,OG,
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=8,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=4,
∴DE=6,
∵DM是⊙O的切线,
∴DN=DE=6,MN=MG,
∴CM=10﹣4﹣MN=6﹣MN,
在Rt△DMC中,DM2=CD2+CM2,
∴(6+NM)2=(6﹣NM)2+82,
∴NM=,
∴DM=6+=.
故答案为:.
16.疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 18 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 (52﹣78) cm.
【分析】延长PQ交FC延长线于点M,先证明△BCE是等边三角形,进而可以求出PF的值;过点Q作QH⊥BM于点H,求出tan15°==2+,进而可以解决问题.
解:如图,延长PQ交FC延长线于点M,
由题意可知:PM⊥AB,∠ABC=60°,
∴∠QMB=30°,
∵Q点是AB中点.
∴QB=AB=10cm,
∴BM=2QB=20cm,QM=QB=10cm,
∵CE=BE=6cm,∠ABC=60°,
∴△BCE是等边三角形,
∴BC=6cm,
∴BD=CD﹣BC=20﹣6=14cm,
∴FM=BM+BD+DF=20+14+20=54(cm),
∴PF=FM=18(cm),
∴当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于18cm,
∴PM=2PF=36cm,
∴PQ=PM﹣QM=36﹣10=26(cm),
当∠P′QB=75°时,P′F得最小高度,如图,延长P′Q交FC延长线于点N,
∴∠N+∠QBN=∠P′QB,
∴∠N=75°﹣60°=15°,
∵∠QMB=30°,
∴∠MQN=15°,
∴∠MQN=∠N=15°,
∴MQ=MN=10cm,
∴FN=FM+MN=(54+10)cm,
如图,过点Q作QH⊥BM于点H,
设OH=xcm,则QM=MN=2xcm,MH=xcm,
∴NH=MN+MH=(2x+x)cm,
∴tan15°==,
∴tan15°==2+,
∴P′F=(2+)(54+10)=(78﹣34)cm,
∴PP′=PF﹣P′F=18﹣(78﹣34)=(52﹣78)cm.
故答案为:18;(52﹣78)cm.
三、解答题(本题共有8小题,共80分,解答题需要写出必要的文字说明、演算步骤)
17.(7)计算:|﹣1|+2cos30°﹣(﹣3)0+()﹣2.
(2)化简:(x﹣2)2﹣x(4﹣x).
【分析】(1)利用绝对值的意义,特殊角的三角函数值,零指数幂的意义和负整数指数幂的意义解答即可;
(2)先利用完全平方公式和单项式乘以多项式的法则去掉括号,再合并同类项即可.
解:(1)原式=1+2×﹣1+4
=1+﹣1+4
=4+;
(2)原式=x2﹣4x+4﹣4x+x2
=2x2﹣8x+4.
18.如图,在△ABC中,BD是△ABC的角平分线,且∠ABC=2∠C.
(1)求证:△ABC∽△ADB.
(2)已知AB=5,AD=4,求BD.
【分析】(1)由BD是△ABC的角平分线得∠ABD=∠DBC=∠ABC,则∠ABC=2∠C得∠C=∠ABC,所以∠C=∠ABD,而∠A是△ABC和△ADB的公共角,则根据“有两个角分别相等的两个三角形相似”可以证明△ABC∽△ADB;
(2)由△ABC∽△ADB得=,其中AB=5,AD=4,可以求出AC的长,再求出CD的长,由∠DBC=∠ABC,∠C=∠ABC,得∠DBC=∠C,则BD=CD,可以求出BD的长.
【解答】(1)证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBC=∠ABC,
∵∠ABC=2∠C,
∴∠C=∠ABC,
∴∠C=∠ABD,
∵∠A=∠A,
∴△ABC∽△ADB.
(2)解:∵△ABC∽△ADB,
∴=,
∵AB=5,AD=4,
∴AC===,
∴CD=AC﹣AD=﹣4=,
∵∠DBC=∠ABC,∠C=∠ABC,
∴∠DBC=∠C,
∴BD=CD=,
∴BD的长为.
19.为了响应国家“双减”政策,温州某学校额外开设了A班电影鉴赏,B班漫画漫游,C班跑步健身三门兴趣课程,小智和小慧需选择一门课程学习.
(1)用列表法或画树状图法,列出小智、小慧两人选课所有可能出现的情况.
(2)求小智、小慧两人同班的概率.
【分析】(1))根据题意画出树状图,即可得出所有等可能的情况数;
(2)由(1)可知,共有9种等可能的结果,其中小智、小慧两人同班的结果有1种,再由概率公式求解即可.
解:(1)根据题意画树状图如下:
则小智、小慧两人选课所有可能出现的情况共有9种;
(2)∵共有9种等可能的情况数,其中小智、小慧两人同班的有3种,
∴小智、小慧两人同班的概率是=.
20.如图,在6×10的方格纸ABCD中有一个格点△EFG,请按要求画线段.
(1)在图1中,过点O画一条格点线段PQ(端点在格点上),使点P,Q分别落在边AD,BC上,且PQ与FG的一边垂直.
(2)在图2中,仅用没有刻度的直尺找出EF上一点M,EG上一点N,连结MN,使△EMN和△EFG的相似比为2:5.(保留作图痕迹)
【分析】(1)利用数形结合的思想画出图形即可;
(2)取格点J,K,连接OJ交EF于点M,连接OK交EG于点N,连接MN即可.
解:(1)如图1中,线段PQ即为所求;
(2)如图2中,线段MN即为所求.
21.如图,抛物线y=﹣x2+8x+m与x轴交于A,B两点,点A的坐标为(1,0).
(1)求抛物线的对称轴及B点坐标;
(2)在y轴的正半轴上有一点E,过点E作x轴的平行线交抛物线于C,D两点,若四边形ABDE为平行四边形,求CD的长.
【分析】(1)把A(1,0)代入y=﹣x2+8x+m,列方程求出m的值为﹣7,则抛物线的解析式为y=﹣x2+8x﹣7,将y=﹣x2+8x﹣7配成顶点式,得到抛物线的对称轴为直线x=4,令y=0,则﹣x2+8x﹣7=0,解方程求出x的值,即得到点B的坐标为(7,0);
(2)作抛物线的对称轴交DE于点F,则点F的横坐标为4,由四边形ABDE为平行四边形,得DE=AB=6,则DF=6﹣4=2,由抛物线的对称性得CF=DF=2,即可求得CD=4.
解:(1)把A(1,0)代入y=﹣x2+8x+m,得﹣1+8+m=0,
解得m=﹣7,
∴抛物线的解析式为y=﹣x2+8x﹣7,
∵y=﹣x2+8x﹣7=﹣(x﹣4)2+9,
∴抛物线的对称轴为直线x=4;
当y=0时,则﹣x2+8x﹣7=0,
解得x1=1,x2=7,
B(7,0).
(2)如图,作抛物线的对称轴交DE于点F,则点F的横坐标为4,
∴EF=4,
∵四边形ABDE为平行四边形,
∴DE=AB=7﹣1=6,
∴CF=DF=6﹣4=2,
∴CD=CF+DF=2+2=4,
∴CD的长为4.
22.如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,以BD为直径的⊙O交AB于点E,交AD的延长线于点F,连结EF,BF.
(1)求证:EF=BF.
(2)若CD:BD=1:3,AC=2,求EF的长.
【分析】(1)先利用圆周角定理得到∠DBF=∠DEB=90°,∠5=∠6,再证明∠4=∠ABF,从而得到∠6=∠ABF,所以EF=BF;
(2)先根据角平分线的性质得到DE=DC,则DE:BD=1:3,接着证明△BDE∽△BAC,利用相似比和比例的性质得到AB=3AC=6,则根据勾股定理可计算出BC=8,于是得到CD=2,AD=2,然后证明△ACD∽△AFB,利用相似比可计算出BF=2,从而得到EF的长.
【解答】(1)证明:连接DE,如图,
∵BD为直径,
∴∠DBF=∠DEB=90°,
∵AD是△ABC的角平分线,
∴∠1=∠2,
∵∠1+∠4=90°,∠2+∠ABF=90°,
∴∠4=∠ABF,
∵∠4=∠5,∠5=∠6,
∴∠6=∠ABF,
∴EF=BF;
(2)解:∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴DE=DC,
∵CD:BD=1:3,
∴DE:BD=1:3,
∵∠DEB=∠C,∠DBE=∠ABC,
∴△BDE∽△BAC,
∴=,
∴==3,
∴AB=3AC=3×2=6,
∴BC===8,
∴CD=BC=2,
∴AD==2,
∵∠1=∠2,∠C=∠AFB,
∴△ACD∽△AFB,
∴=,即=,
∴BF=2,
∴EF=2.
23.抗疫期间,全国人民众志成城,温州某商家决定将一个月的利润全部捐给当地医疗机构用于抗疫.该商家购进一批产品,成本10元/件,分为线上和线下两种销售方式.线下市场调查发现,当售价为12元时,月销量1200件,售价每增加1元,月销量减少100件.设月销量y(件),线下售价x(元).(12≤x≤24,且x为整数)
(1)求y关于x的函数关系式;
(2)若线上售价与线下相同,但每件产品商家需多付2元快递费,且线上月销量固定为500件.
①当售价x为多少时,线上和线下的月利润总和最大?并求出最大利润.
②商家第二个月决定继续捐款支持抗疫,捐款方式变为每卖出一件产品就捐款a元,为使商家线上和线下的月利润最低为700元,则a= 1 .(直接写出答案)
【分析】(1)根据月销量=1200﹣月销量减小件数求解.
(2)①根据月利润总和=线上利润+线下利润列出利润总和与x的关系,解析式化为顶点式求解.
②分类讨论x=12和x=24时商家月利润为700时求出a的值.
解:(1)根据题意得:y=1200﹣100(x﹣12)=﹣100x+2400,
∴y关于x的函数关系式为y=﹣100x+2400;
(2)①设线上和线下的月利润总和为w元,则
w=500(x﹣10﹣2)+y(x﹣10)
=500x﹣6000+(﹣100x+2400)(x﹣10)
=﹣100x2+3900x﹣30000,
=﹣100(x﹣)2+8025,
∵﹣100<0,12≤x≤24,且x为整数,
∴当x=19或20时,w有最大值,最大值为8000,
∴当x为19或20时,线上和线下的月利润总和达到最大,最大利润为8000元;
②设商家线上和线下的月利润总和为w元,
根据题意得,w=500(x﹣2﹣10﹣a)+(x﹣10﹣a)(﹣100x+2400),
即w=﹣100x2+(3900+100a)x﹣30000﹣2900a,
∵﹣100<0,抛物线开口向下,
∴x==,
当x=12,w取最小值为700时,700=﹣100×122+12×3900+12×100a﹣30000﹣2900a,
解得a=1,
此时抛物线对称轴为直线x==20,
20﹣12>24﹣20,满足题意.
当x=24,w取最小值为700时,700=﹣100×242+3900×24+24×100a﹣30000﹣2900a,
解得a=10.6,
此时抛物线对称轴为直线x==24.8,
24.8﹣24>24.8﹣12,不满足题意.
故答案为:1.
24.在菱形ABCD中,对角线AC和BD相交于点O,且AC=16,BD=12.动点P从点A出发以2.5cm/s的速度沿折线A一B一C的路线向终点C运动.过点P作PQ⊥AC,垂足为Q,点Q关于点O的对称点为M,过点P,Q,M作⊙I.设运动时间为t秒.
(1)当t=1时,求AQ和PQ的长.
(2)当P为AB中点时,请判断点B与⊙I的位置关系,并说明理由.
(3)在点P的整个运动过程中.
①当t为何值时,⊙I经过点B.
②当t= 4或 时,⊙I与边AB相切.
【分析】(1)利用菱形的性质及勾股定理求出OA、OB、AB的长度,根据题意求出AP的长度,再利用相似三角形的判断与性质即可求出AQ和PQ的长度;
(2)利用菱形的性质、对称的性质求出⊙I的半径和IB的长度,通过比较即可判断出点B与⊙I的位置关系;
(3)①根据题意先表示出OQ和OI的长度,进而表示出半径r,求出BI的长度,利用BI=r,列出方程,解方程即可求出t的值;
②⊙I与AB相切,则与AC也相切,对出切点为P,求出BP的长,表示出r,由①得出r,进而得出方程,解方程即可得出t的值.
解:(1)如图1,
∵四边形ABCD是菱形,AC=16,BD=12,
∴AC⊥BD,AO=AC=×16=8,BO=BD=×12=6,
∴AB===10,
∵PQ⊥AC,
∴∠AQP=∠AOB=90°,
∵∠QAP=∠OAB,
∴△AQP∽△AOB,
∴,
当t=1时,AP=2.5×1=2.5,
∴,,
∴AQ=2,PQ=1.5;
(2)如图2,
点B在⊙I外,理由如下:
连接PM交OB与点I,
当P为AB中点时,
OQ=AO=×8=4,PQ=BO=×6=3,
∵点Q关于点O的对称点为M,
∴QM=2OA=2×4=8,
∵PQ⊥OA,
∴PM为⊙I的直径,I为圆心,PM===,
∴⊙I的半径r=,
∵O是QM的中点,I是PM的中点,
∴OI是△MQP的中位线,
∴OI=PQ=×3=,
∴IB=OB﹣OI=6﹣=>r,
∴点B在⊙I外.
(3)①∵OQ=AO﹣AQ=AO﹣,
OI=,
∴r=,
BI=OB﹣OI=6﹣,
若⊙I经过点B,则BI=r,
∴BI2=r2,
∴t2﹣32t+64=(6﹣t)2,
∴4t2﹣23t+28=0,
解得:t=4或t=,
∴当t为4或时,⊙I经过点B;
②r=,
∵⊙I与AB相切,
∴⊙I与AC也相切,与AB的切点为P,则BP=AB﹣AP=10﹣2.5t,
∵r=,
∴,
∴,
解得:t=4或t=,
∴当t=4或t=时,⊙I与边AB相切,
故答案为:4或.
同课章节目录
