8.3.2 圆柱、圆锥、圆台、球的表面积和体积(共28张PPT)
文档属性
| 名称 | 8.3.2 圆柱、圆锥、圆台、球的表面积和体积(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 841.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 11:06:05 | ||
图片预览







文档简介
(共28张PPT)
第八章
8.3.2 圆柱、圆锥、圆台、球的表面积和体积
1.知道圆柱、圆锥、圆台和球的表面积和体积的计算公式.
2.能用公式解决简单的实际问题.
课标要求
素养要求
在计算圆柱、圆锥、圆台、球的表面积和体积的过程中,要把实际问题转化为数学问题,并进行计算,发展学生的数学建模、数学运算和直观想象素养.
课前预习
知识探究
1
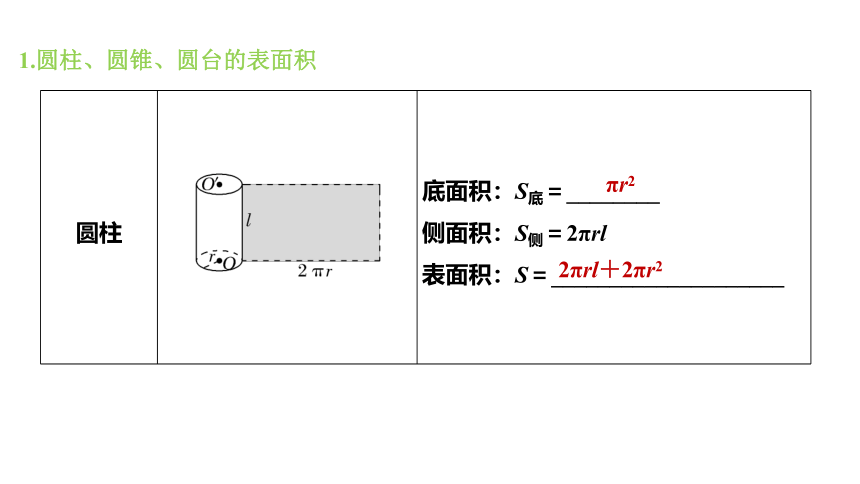
1.圆柱、圆锥、圆台的表面积
圆柱 底面积:S底=________
侧面积:S侧=2πrl
表面积:S=____________________
πr2
2πrl+2πr2
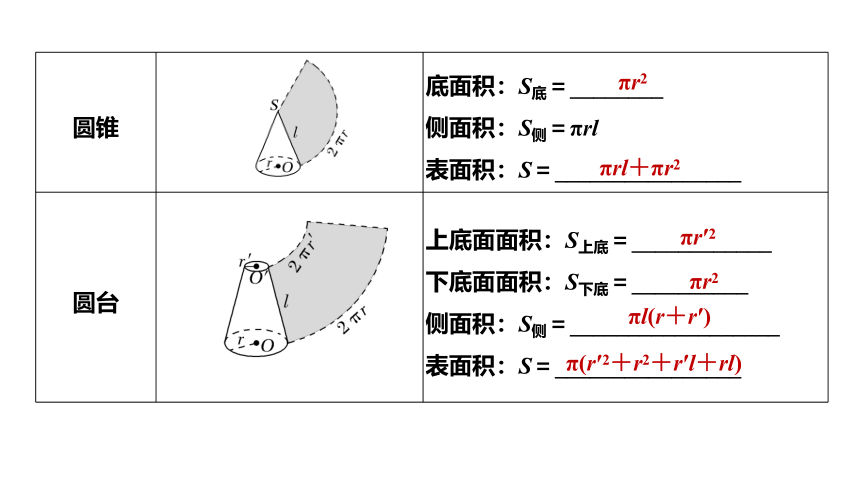
圆锥 底面积:S底=________
侧面积:S侧=πrl
表面积:S=________________
圆台 上底面面积:S上底=____________
下底面面积:S下底=__________
侧面积:S侧=__________________
表面积:S=________________
πr2
πrl+πr2
πr′2
πr2
πl(r+r′)
π(r′2+r2+r′l+rl)
2.圆柱、圆锥、圆台的体积公式
3.球的表面积与体积公式
4πR2
1.思考辨析,判断正误
(1)圆锥的侧面展开图为扇形,其中扇形的弧长为圆锥底面圆的周长.( )
(2)若圆柱的底面圆的直径与圆柱的高相等,则圆柱的侧面展开图是正方形.( )
(3)求圆台的表面积和体积时,常用“还台为锥”的思想方法.( )
(4)两个球的半径之比为1∶2,则其体积之比为1∶4.( )
提示 (2)设圆柱的底面圆的半径为r,所以圆柱的侧面展开图的相邻两边长分别为2πr,2r,二者不相等,故侧面展开图不是正方形.
(4)两球的体积之比V1∶V2=r∶r=1∶8.
√
×
√
×
C
A
C
课堂互动
题型剖析
2
题型一 求圆柱、圆锥、圆台的表面积
【例1】 (1)若圆锥的高和底面半径相等,它的一个内接圆柱的高和圆柱底面半径也相等.则圆柱的表面积和圆锥的表面积之比为________.
解析 如图所示,
(2)若圆台的上、下底面半径分别为2,6,且侧面面积等于两底面面积之和,则圆台的母线长为________,表面积为________.
5
80π
解析 设圆台的母线长为l,则由题意得
π(2+6)l=π×22+π×62,
∴8πl=40π,∴l=5,
∴该圆台的母线长为5.
圆台的表面积为
S=π×(2+6)×5+π·22+π×62
=40π+4π+36π
=80π.
圆柱、圆锥、圆台的表面积的求解步骤,解决圆柱、圆锥、圆台的表面积问题,要利用好旋转体的轴截面及侧面展开图,借助于平面几何知识,求得所需几何要素,代入公式求解即可,基本步骤如下:
(1)得到空间几何体的平面展开图;
(2)依次求出各个平面图形的面积;
(3)将各平面图形的面积相加.
思维升华
解析 设圆锥底面圆的半径为r,高为h,母线长为l.
A
【例2】 设圆台的高为3,如图,在轴截面中母线AA1与底面直径AB的夹角为60°,轴截面中的一条对角线垂直于腰,则圆台的体积为________.
题型二 求圆柱、圆锥、圆台的体积
21π
解析 设上、下底面半径,母线长分别为r,R,l.
作A1D⊥AB于点D,则A1D=3,∠A1AB=60°,
又∠BA1A=90°,∴∠BA1D=60°,
=21π.
∴圆台的体积为21π.
求圆柱、圆锥、圆台的体积的关键是求其底面面积和高,其中高一般利用几何体的轴截面求得,一般是在由母线、高、半径组成的直角三角形中列出方程并求解.
思维升华
D
题型三 球的表面积和体积
∴AB2+AC2=BC2,即△ABC为直角三角形.
∴平面ABC被球所截得的图形是以BC为直径的圆.
由已知球心O与截面圆圆心的距离为4,
1.公式是计算球的表面积和体积的关键,半径与球心是确定球的条件.
2.两个结论:①两个球的表面积之比等于这两个球的半径比的平方;②两个球的体积之比等于这两个球的半径比的立方.
思维升华
解析 设球心为O,截面圆心为O1,连接OO1.
则OO1垂直于截面圆O1,如图所示.
在Rt△OO1A中,
B
题型四 求组合体的表面积和体积
【例4】 如图所示,在边长为4的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D,H,G为垂足,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积和体积.
所求旋转体的体积为大圆锥的体积减去里面小圆柱的体积,
求组合体的表面积和体积.首先要认清组合体是由哪些简单几何体构成的,组合体的表面积是可见的围成组合体的所有面的面积之和,但不一定是组合体的几个简单几何体的表面积之和;组合体的体积是构成组合体的几个简单组合体的体积之和(差).
思维升华
解析 ∵一个正四棱柱的各个顶点都在一个半径为2 cm的球面上,正四棱柱的底面边长为2 cm,球的直径为正四棱柱的体对角线,
B
1.解决圆柱、圆锥、圆台的表面积问题,要利用好旋转体的轴截面及侧面展开图,借助平面几何知识,求得所需几何要素,代入公式求解.
2.圆柱、圆锥、圆台的体积和侧面积之间的关系
(1)体积之间的关系
课堂小结
3.计算球的表面积、体积的关键是求出球的半径.在解决有关球的截面问题时,要注意截面性质的应用.
4.在解决与球有关的组合体问题时,要注意切、接性质不同,有时也根据组合体的几何性质作出截面,把关键量转化到一个平面上来处理.
第八章
8.3.2 圆柱、圆锥、圆台、球的表面积和体积
1.知道圆柱、圆锥、圆台和球的表面积和体积的计算公式.
2.能用公式解决简单的实际问题.
课标要求
素养要求
在计算圆柱、圆锥、圆台、球的表面积和体积的过程中,要把实际问题转化为数学问题,并进行计算,发展学生的数学建模、数学运算和直观想象素养.
课前预习
知识探究
1
1.圆柱、圆锥、圆台的表面积
圆柱 底面积:S底=________
侧面积:S侧=2πrl
表面积:S=____________________
πr2
2πrl+2πr2
圆锥 底面积:S底=________
侧面积:S侧=πrl
表面积:S=________________
圆台 上底面面积:S上底=____________
下底面面积:S下底=__________
侧面积:S侧=__________________
表面积:S=________________
πr2
πrl+πr2
πr′2
πr2
πl(r+r′)
π(r′2+r2+r′l+rl)
2.圆柱、圆锥、圆台的体积公式
3.球的表面积与体积公式
4πR2
1.思考辨析,判断正误
(1)圆锥的侧面展开图为扇形,其中扇形的弧长为圆锥底面圆的周长.( )
(2)若圆柱的底面圆的直径与圆柱的高相等,则圆柱的侧面展开图是正方形.( )
(3)求圆台的表面积和体积时,常用“还台为锥”的思想方法.( )
(4)两个球的半径之比为1∶2,则其体积之比为1∶4.( )
提示 (2)设圆柱的底面圆的半径为r,所以圆柱的侧面展开图的相邻两边长分别为2πr,2r,二者不相等,故侧面展开图不是正方形.
(4)两球的体积之比V1∶V2=r∶r=1∶8.
√
×
√
×
C
A
C
课堂互动
题型剖析
2
题型一 求圆柱、圆锥、圆台的表面积
【例1】 (1)若圆锥的高和底面半径相等,它的一个内接圆柱的高和圆柱底面半径也相等.则圆柱的表面积和圆锥的表面积之比为________.
解析 如图所示,
(2)若圆台的上、下底面半径分别为2,6,且侧面面积等于两底面面积之和,则圆台的母线长为________,表面积为________.
5
80π
解析 设圆台的母线长为l,则由题意得
π(2+6)l=π×22+π×62,
∴8πl=40π,∴l=5,
∴该圆台的母线长为5.
圆台的表面积为
S=π×(2+6)×5+π·22+π×62
=40π+4π+36π
=80π.
圆柱、圆锥、圆台的表面积的求解步骤,解决圆柱、圆锥、圆台的表面积问题,要利用好旋转体的轴截面及侧面展开图,借助于平面几何知识,求得所需几何要素,代入公式求解即可,基本步骤如下:
(1)得到空间几何体的平面展开图;
(2)依次求出各个平面图形的面积;
(3)将各平面图形的面积相加.
思维升华
解析 设圆锥底面圆的半径为r,高为h,母线长为l.
A
【例2】 设圆台的高为3,如图,在轴截面中母线AA1与底面直径AB的夹角为60°,轴截面中的一条对角线垂直于腰,则圆台的体积为________.
题型二 求圆柱、圆锥、圆台的体积
21π
解析 设上、下底面半径,母线长分别为r,R,l.
作A1D⊥AB于点D,则A1D=3,∠A1AB=60°,
又∠BA1A=90°,∴∠BA1D=60°,
=21π.
∴圆台的体积为21π.
求圆柱、圆锥、圆台的体积的关键是求其底面面积和高,其中高一般利用几何体的轴截面求得,一般是在由母线、高、半径组成的直角三角形中列出方程并求解.
思维升华
D
题型三 球的表面积和体积
∴AB2+AC2=BC2,即△ABC为直角三角形.
∴平面ABC被球所截得的图形是以BC为直径的圆.
由已知球心O与截面圆圆心的距离为4,
1.公式是计算球的表面积和体积的关键,半径与球心是确定球的条件.
2.两个结论:①两个球的表面积之比等于这两个球的半径比的平方;②两个球的体积之比等于这两个球的半径比的立方.
思维升华
解析 设球心为O,截面圆心为O1,连接OO1.
则OO1垂直于截面圆O1,如图所示.
在Rt△OO1A中,
B
题型四 求组合体的表面积和体积
【例4】 如图所示,在边长为4的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D,H,G为垂足,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积和体积.
所求旋转体的体积为大圆锥的体积减去里面小圆柱的体积,
求组合体的表面积和体积.首先要认清组合体是由哪些简单几何体构成的,组合体的表面积是可见的围成组合体的所有面的面积之和,但不一定是组合体的几个简单几何体的表面积之和;组合体的体积是构成组合体的几个简单组合体的体积之和(差).
思维升华
解析 ∵一个正四棱柱的各个顶点都在一个半径为2 cm的球面上,正四棱柱的底面边长为2 cm,球的直径为正四棱柱的体对角线,
B
1.解决圆柱、圆锥、圆台的表面积问题,要利用好旋转体的轴截面及侧面展开图,借助平面几何知识,求得所需几何要素,代入公式求解.
2.圆柱、圆锥、圆台的体积和侧面积之间的关系
(1)体积之间的关系
课堂小结
3.计算球的表面积、体积的关键是求出球的半径.在解决有关球的截面问题时,要注意截面性质的应用.
4.在解决与球有关的组合体问题时,要注意切、接性质不同,有时也根据组合体的几何性质作出截面,把关键量转化到一个平面上来处理.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
