27.2.1相似三角形的判定(4)
文档属性
| 名称 | 27.2.1相似三角形的判定(4) |  | |
| 格式 | zip | ||
| 文件大小 | 138.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-23 21:31:08 | ||
图片预览


文档简介
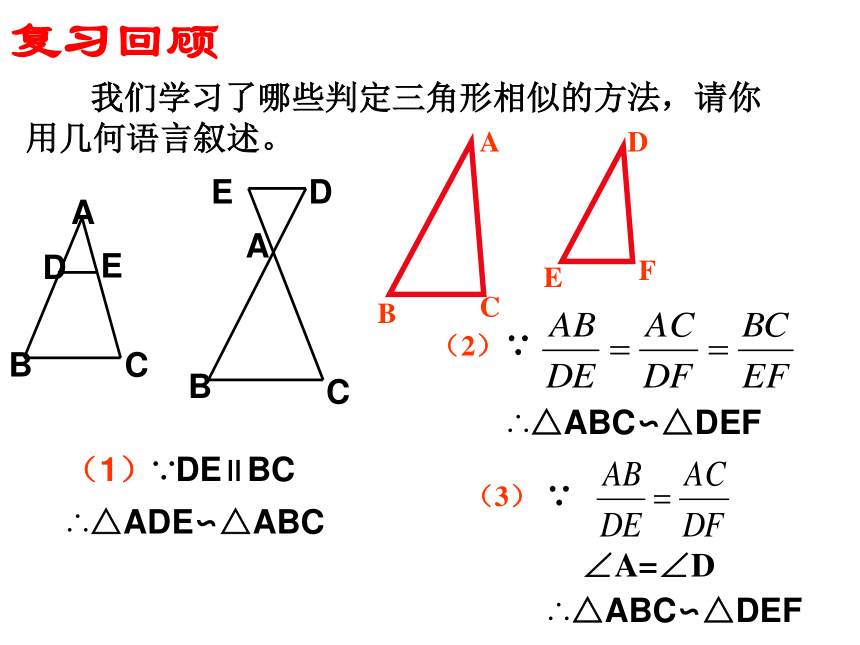
课件16张PPT。27.2.1相似三角形的判定(4)(1)∵DE∥BC
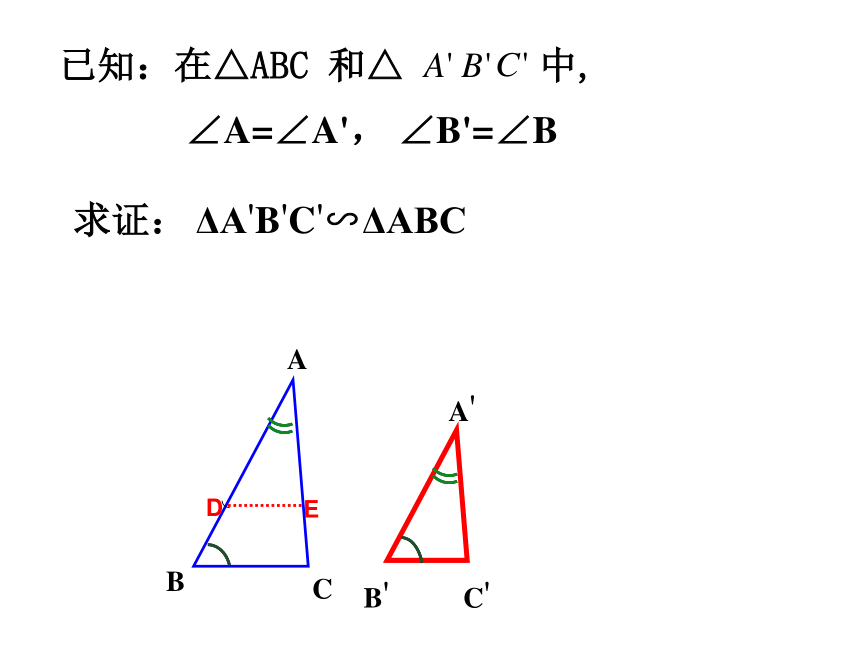
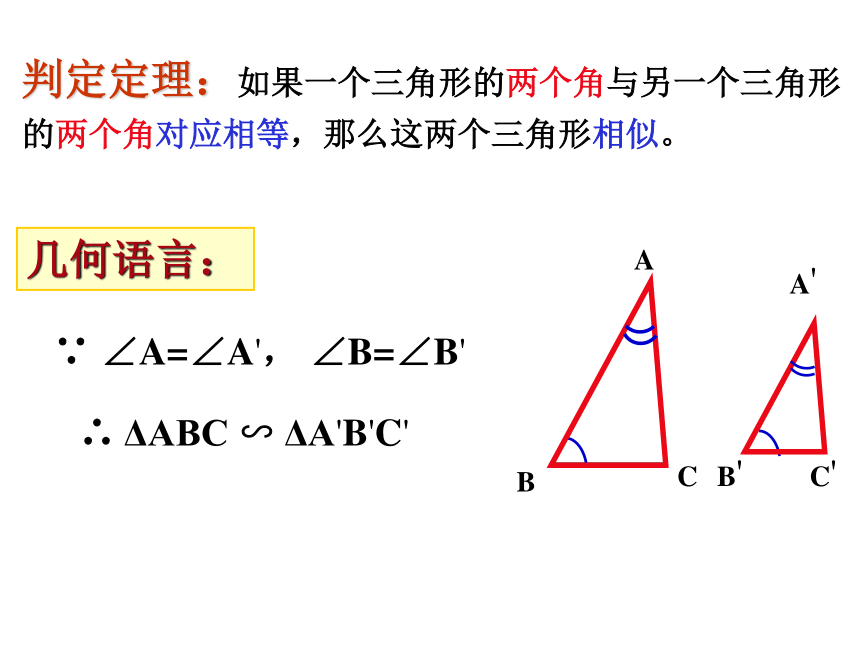
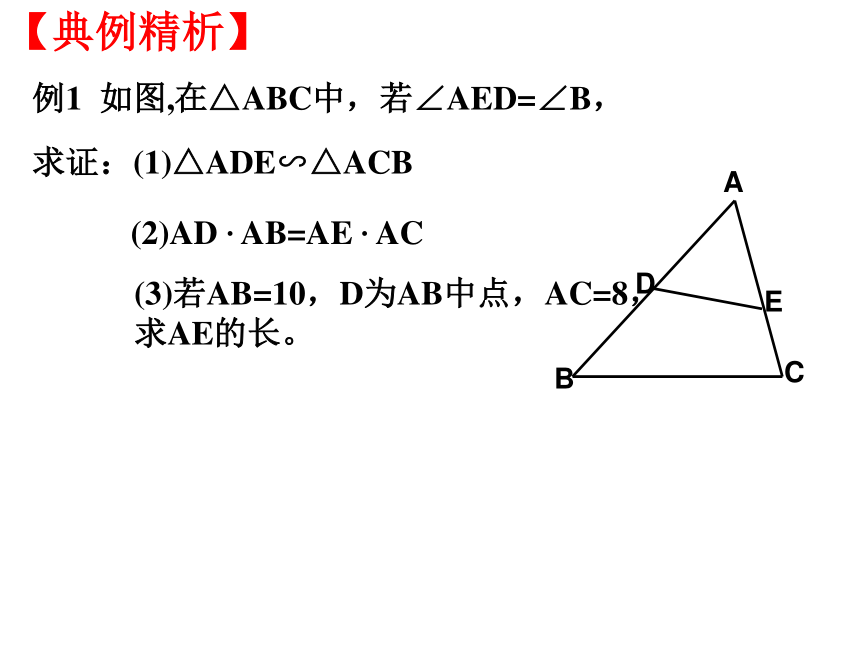
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用几何语言叙述。复习回顾(2)∵∴△ABC∽△DEF(3) ∵∠A=∠D∴△ABC∽△DEF观察: 观察两个含30°角的三角尺。 一般地,如果两个三角形有两组对应角相等,它们一定相似吗?发现:两个三角尺大小不同,但它们看起来是相似的。问题:已知:在△ABC 和△ 中, ∠A=∠A', ∠B'=∠B求证: ΔA'B'C'∽ΔABCDECC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'几何语言:判定定理:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。【典例精析】例1 如图,在△ABC中,若∠AED=∠B,
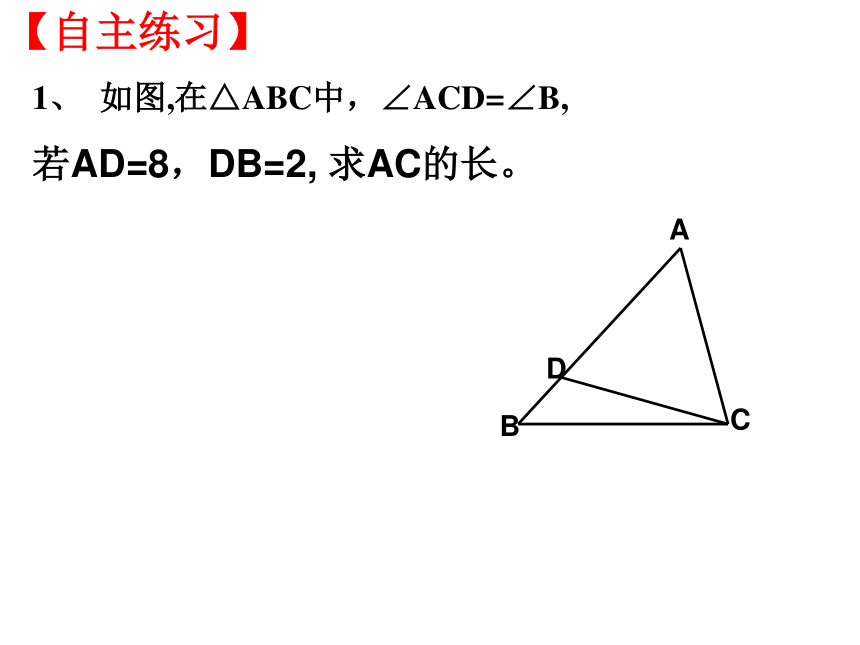
求证:(1)△ADE∽△ACB(2)AD . AB=AE . AC(3)若AB=10,D为AB中点,AC=8,求AE的长。【自主练习】1、 如图,在△ABC中,∠ACD=∠B,
若AD=8,DB=2, 求AC的长。
例2 如图,弦AB和CD相交于圆O内一点P。
求证:PA ? PB = PC?PD【典例精析】例2 如图,弦AB和CD相交于圆O内一点P。
求证:PA ? PB = PC?PD【典例精析】你能证明吗?【自主练习】PA ? PB = PC?PD例3 求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:求证:(1)AC2=AD · AB;求证:(2)CD2=AD · DB引申【典例精析】BC2=BD · AB请记住以上结论DBCA18 【自主练习】2、如图,点C是半圆的直径AB上的一点,CD⊥AB,垂足为D,若AC=2,AB=10,求CD的长【自主练习】┓28总结反思 与大家分享一下本节课你的收获! 3、学会了利用相似证明等积式1、学习了两角相等证相似2、认识了三个相似基本图4、体会到等量代换在等积式证明中的作用老师的总结例4. 如图,在正方形ABCD中,点E为DB上一点,AE的延长线交DC于F,交BC的延长线于G。
试说明AE2=EF . EG。【拓展提高】E1、作业本(1) P12---13
2、课时作业本 P48---49 今天作业
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用几何语言叙述。复习回顾(2)∵∴△ABC∽△DEF(3) ∵∠A=∠D∴△ABC∽△DEF观察: 观察两个含30°角的三角尺。 一般地,如果两个三角形有两组对应角相等,它们一定相似吗?发现:两个三角尺大小不同,但它们看起来是相似的。问题:已知:在△ABC 和△ 中, ∠A=∠A', ∠B'=∠B求证: ΔA'B'C'∽ΔABCDECC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'几何语言:判定定理:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。【典例精析】例1 如图,在△ABC中,若∠AED=∠B,
求证:(1)△ADE∽△ACB(2)AD . AB=AE . AC(3)若AB=10,D为AB中点,AC=8,求AE的长。【自主练习】1、 如图,在△ABC中,∠ACD=∠B,
若AD=8,DB=2, 求AC的长。
例2 如图,弦AB和CD相交于圆O内一点P。
求证:PA ? PB = PC?PD【典例精析】例2 如图,弦AB和CD相交于圆O内一点P。
求证:PA ? PB = PC?PD【典例精析】你能证明吗?【自主练习】PA ? PB = PC?PD例3 求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:求证:(1)AC2=AD · AB;求证:(2)CD2=AD · DB引申【典例精析】BC2=BD · AB请记住以上结论DBCA18 【自主练习】2、如图,点C是半圆的直径AB上的一点,CD⊥AB,垂足为D,若AC=2,AB=10,求CD的长【自主练习】┓28总结反思 与大家分享一下本节课你的收获! 3、学会了利用相似证明等积式1、学习了两角相等证相似2、认识了三个相似基本图4、体会到等量代换在等积式证明中的作用老师的总结例4. 如图,在正方形ABCD中,点E为DB上一点,AE的延长线交DC于F,交BC的延长线于G。
试说明AE2=EF . EG。【拓展提高】E1、作业本(1) P12---13
2、课时作业本 P48---49 今天作业
