27.2.1 相似三角形的判定(5)
文档属性
| 名称 | 27.2.1 相似三角形的判定(5) |  | |
| 格式 | zip | ||
| 文件大小 | 42.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-23 21:33:41 | ||
图片预览


文档简介
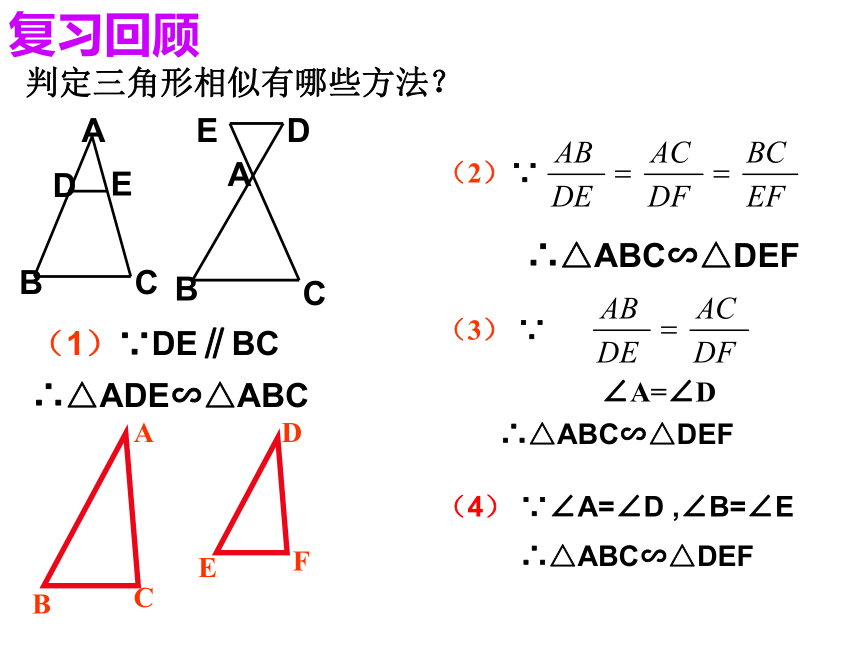
课件12张PPT。27.2.1相似三角形(5)(1)∵DE∥BC
∴△ADE∽△ABC判定三角形相似有哪些方法?复习回顾(2)∵∴△ABC∽△DEF(3) ∵∠A=∠D∴△ABC∽△DEF(4) ∵∠A=∠D ,∠B=∠E∴△ABC∽△DEF思考
对于直角三角形,我们还可以用“HL”判定全等,那么,满足斜边的比等于一组直角边的比的两个直角三角形相似吗?问题
对于两个直角三角形,只要两组对应边的比相等,那么这两个直角三角形一定相似。
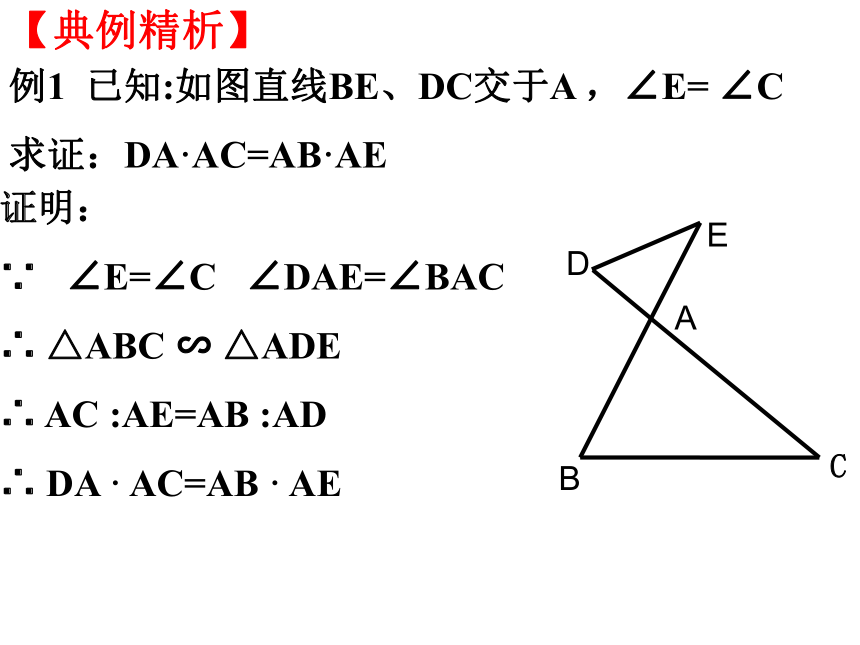
这句话对吗?例1 已知:如图直线BE、DC交于A ,∠E= ∠C
求证:DA·AC=AB·AE证明:
∵ ∠E=∠C ∠DAE=∠BAC
∴ △ABC ∽ △ADE
∴ AC :AE=AB :AD
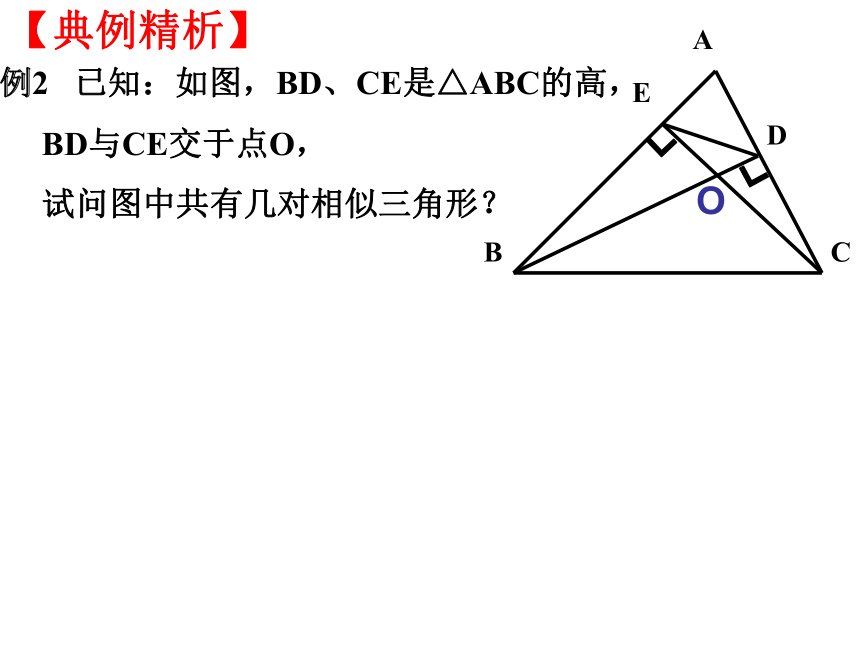
∴ DA · AC=AB · AE【典例精析】例2 已知:如图,BD、CE是△ABC的高,
BD与CE交于点O,
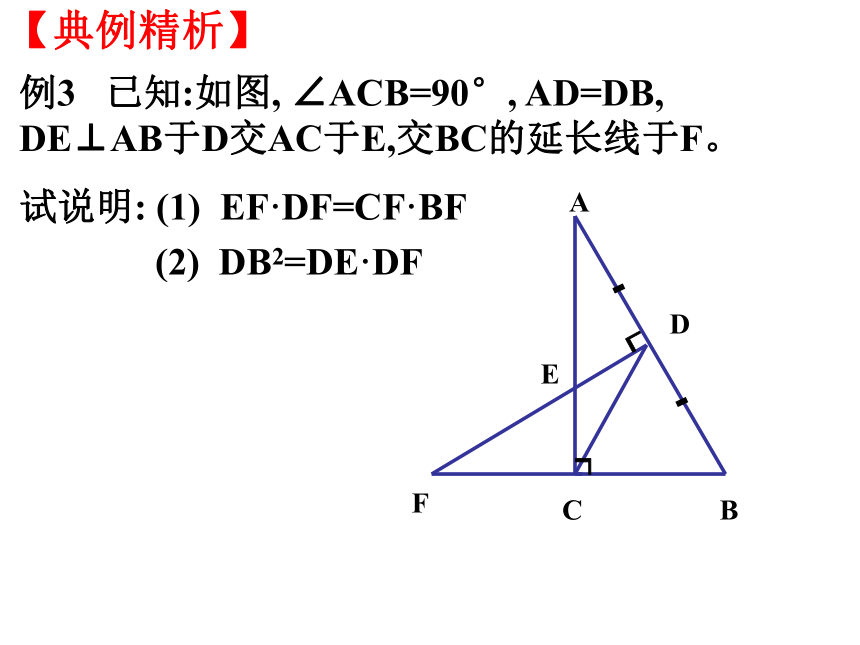
试问图中共有几对相似三角形?┏┏【典例精析】O例3 已知:如图, ∠ACB=90°, AD=DB, DE⊥AB于D交AC于E,交BC的延长线于F。
试说明: (1) EF·DF=CF·BF (2) DB2=DE·DF【典例精析】┑┑--11、已知DE ∥BC 且∠1=∠B ,则图中共有 对相似三角形。∵ DE∥BC∴△ADE∽△ABC∵ ∠1=∠B ,∠A=∠A ∴△ACD∽△ABC∴△ADE ∽△ACD∵ DE∥BC∵ ∠EDC=∠DCB, 又∵ ∠1=∠B∴△DEC∽△CDB4【自主练习】2、如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于D,交BC于E,连接BD、CD。
求证(1)AB·AC=AE·AD
(2)BD2=DE·AD
【自主练习】总结反思 与大家分享一下本节课你的收获! 1、复习了证相似的方法2、学会了证明比例式或等积式的方法3、体会到转化思想、分类讨论思想在解题中的作用老师的总结转化为证相似课时作业本 P50---51 今天作业如图(10)所示:等边△ABC中,线段AD为其内角平分线,过点D的直线B1C1⊥AC于C1,交AB延长线于B1.
(1)请你探究: 、 是否成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角平分线,请问 一定成立吗?并证明你的判断.
(3)如图(2)所示,在Rt△ABC中,∠ACB=90°,AC=8, ,E为AB上一点且AE=5,CE交其内角平分线AD于点F。试求 的值。例4、1 12012年湖北黄石6.如图,已知抛物线: y=- (x+2)(x-m)(m>0)与x 轴相交于点B、
C,与y 轴相交于点E,且点B 在点C 的左侧.
(1)若抛物线过点M(2,2),求实数m 的值.
(2)在(1)的条件下,求△BCE的面积.
(4)在第四象限内,抛物线上是否存在点F,使得以点B、C、F 为顶点的三角形与△BCE 相似?若存在,求m 的值;若不存在,请说明理由.
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使BH+EH 最小,并求出点H 的坐标.【典例精析】
∴△ADE∽△ABC判定三角形相似有哪些方法?复习回顾(2)∵∴△ABC∽△DEF(3) ∵∠A=∠D∴△ABC∽△DEF(4) ∵∠A=∠D ,∠B=∠E∴△ABC∽△DEF思考
对于直角三角形,我们还可以用“HL”判定全等,那么,满足斜边的比等于一组直角边的比的两个直角三角形相似吗?问题
对于两个直角三角形,只要两组对应边的比相等,那么这两个直角三角形一定相似。
这句话对吗?例1 已知:如图直线BE、DC交于A ,∠E= ∠C
求证:DA·AC=AB·AE证明:
∵ ∠E=∠C ∠DAE=∠BAC
∴ △ABC ∽ △ADE
∴ AC :AE=AB :AD
∴ DA · AC=AB · AE【典例精析】例2 已知:如图,BD、CE是△ABC的高,
BD与CE交于点O,
试问图中共有几对相似三角形?┏┏【典例精析】O例3 已知:如图, ∠ACB=90°, AD=DB, DE⊥AB于D交AC于E,交BC的延长线于F。
试说明: (1) EF·DF=CF·BF (2) DB2=DE·DF【典例精析】┑┑--11、已知DE ∥BC 且∠1=∠B ,则图中共有 对相似三角形。∵ DE∥BC∴△ADE∽△ABC∵ ∠1=∠B ,∠A=∠A ∴△ACD∽△ABC∴△ADE ∽△ACD∵ DE∥BC∵ ∠EDC=∠DCB, 又∵ ∠1=∠B∴△DEC∽△CDB4【自主练习】2、如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于D,交BC于E,连接BD、CD。
求证(1)AB·AC=AE·AD
(2)BD2=DE·AD
【自主练习】总结反思 与大家分享一下本节课你的收获! 1、复习了证相似的方法2、学会了证明比例式或等积式的方法3、体会到转化思想、分类讨论思想在解题中的作用老师的总结转化为证相似课时作业本 P50---51 今天作业如图(10)所示:等边△ABC中,线段AD为其内角平分线,过点D的直线B1C1⊥AC于C1,交AB延长线于B1.
(1)请你探究: 、 是否成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角平分线,请问 一定成立吗?并证明你的判断.
(3)如图(2)所示,在Rt△ABC中,∠ACB=90°,AC=8, ,E为AB上一点且AE=5,CE交其内角平分线AD于点F。试求 的值。例4、1 12012年湖北黄石6.如图,已知抛物线: y=- (x+2)(x-m)(m>0)与x 轴相交于点B、
C,与y 轴相交于点E,且点B 在点C 的左侧.
(1)若抛物线过点M(2,2),求实数m 的值.
(2)在(1)的条件下,求△BCE的面积.
(4)在第四象限内,抛物线上是否存在点F,使得以点B、C、F 为顶点的三角形与△BCE 相似?若存在,求m 的值;若不存在,请说明理由.
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使BH+EH 最小,并求出点H 的坐标.【典例精析】
