27.2.1 相似三角形的判定
文档属性
| 名称 | 27.2.1 相似三角形的判定 |  | |
| 格式 | zip | ||
| 文件大小 | 363.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-23 22:58:48 | ||
图片预览





文档简介
课件20张PPT。27.2.1 相似三角形的判定
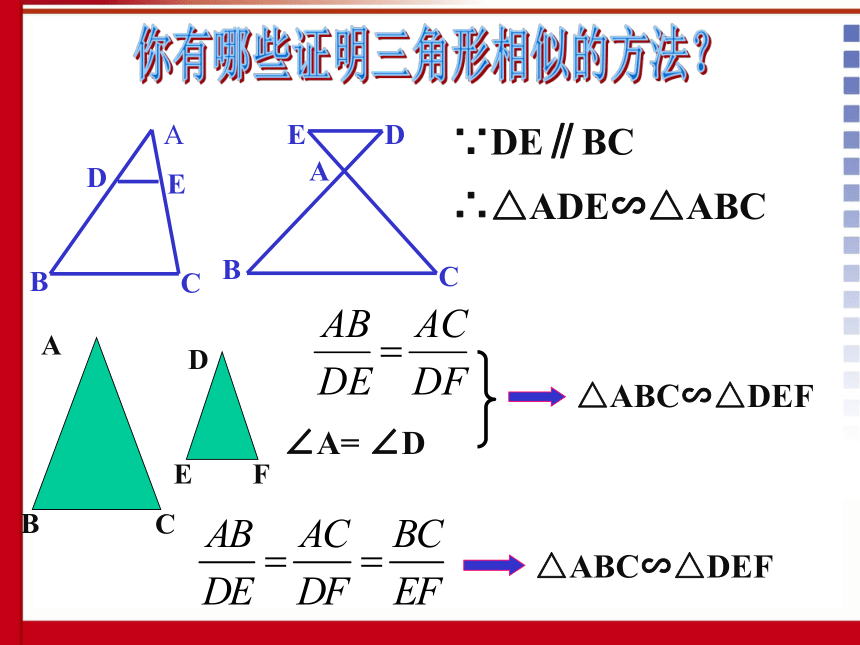
(AA)∵DE∥BC ∴△ADE∽△ABC∠A= ∠D△ABC∽△DEF△ABC∽△DEF你有哪些证明三角形相似的方法?(1)我们已学习过哪些判定三角形相似的方法?(3)如(2)题图,△ABC中,点D在AB上,如果∠ACD=∠B,
那么△ACD与△ABC相似吗? 理由:∵AC2=AD?AB又∠A=∠A(2)如图,△ABC中,点D在AB上,如果AC2=AD?AB,那么△ACD与△ABC相似吗?
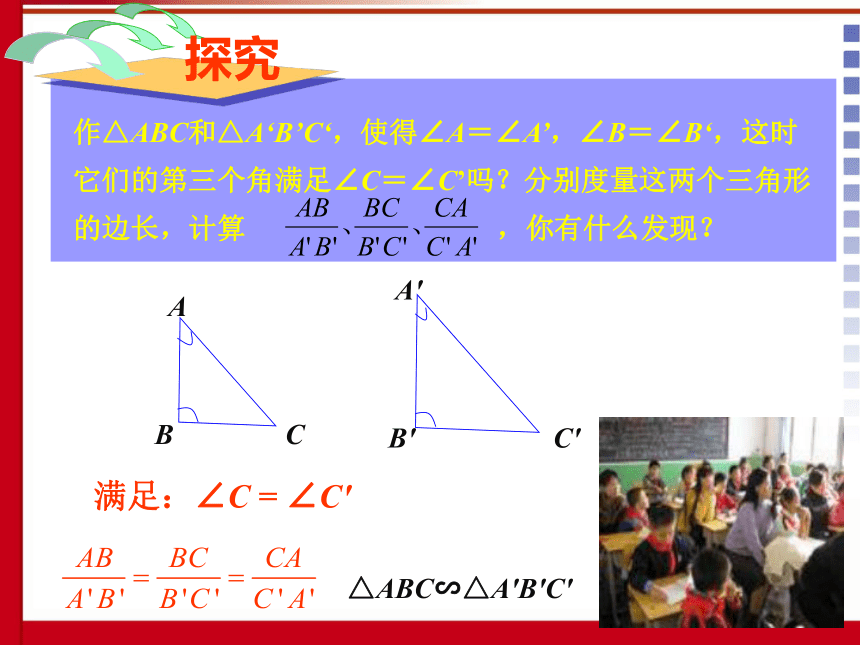
说说你的理由.相似三角形满足对应角相等,对应边的比相等,那么这两个三角形相似.相似解:相似知识链接∴△ACD∽△ABC平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.如果两个三角形的三组对应边的比相等,那么这两个三角形相似.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似. 观察两副三角尺如图,其中同样角度(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.一般地,如果两个三角形有两组对应角相等,它们一定相似吗?观 察作△ABC和△A‘B’C‘,使得∠A=∠A’,∠B=∠B‘,这时它们的第三个角满足∠C=∠C’吗?分别度量这两个三角形的边长,计算 ,你有什么发现?满足:∠C = ∠C'△ABC∽△A'B'C' 把你的结果与邻座的同学比较,你们的结论一样吗? △ABC和△A'B'C'相似吗?一样△ABC和△A'B'C'相似得到判定两个三角形相似的又一个简便方法:如图,已知△ABC和△A'B'C'中,∠A=∠A', ∠B=∠B',
求证: △ABC∽△A'B'C'证明:在△ABC的边AB(或延长线)上,截取AD=A'B',过点D
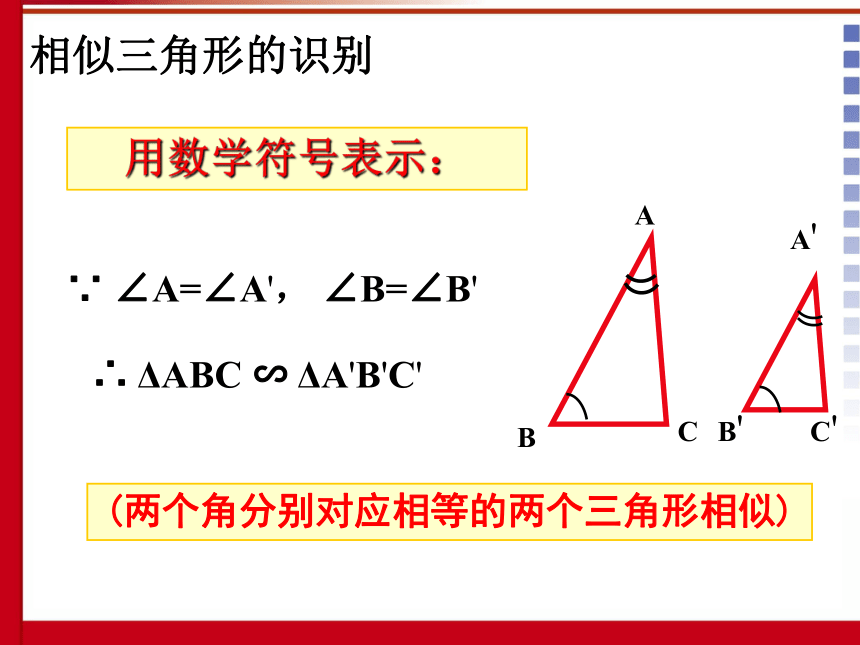
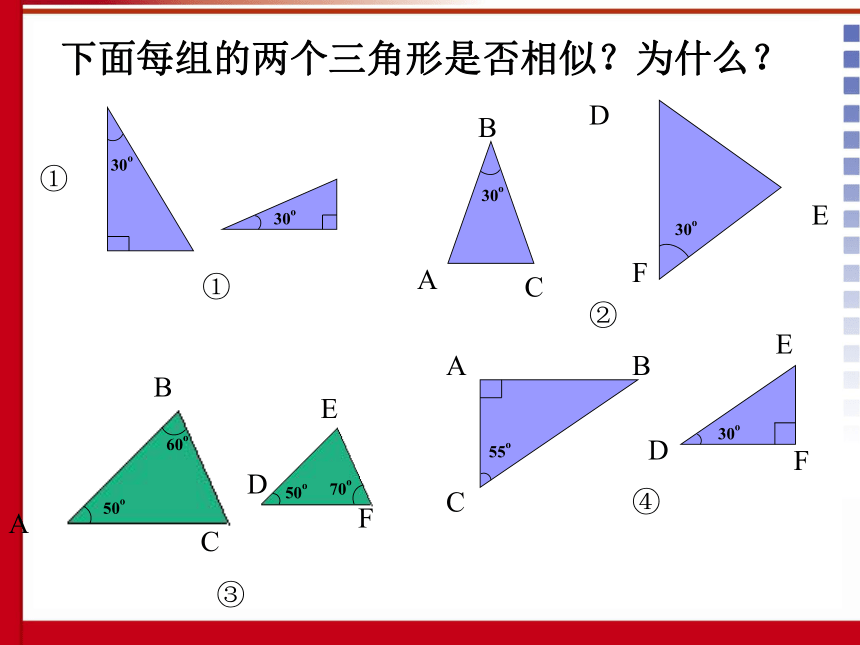
作DE//BC,交AC于点E,则有△ADE∽△ABC∵∠ADE=∠B, ∠B=∠B'∴∠ADE=∠B'又∵∠A=∠A',AD=A'B'∴△ADE≌△A'B'C'∴△A'B'C'∽△ABCCC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别(两个角分别对应相等的两个三角形相似)下面每组的两个三角形是否相似?为什么?①①②③④ABCFDEACBDEFBACDFE30o30o30o30o55o30o例1、 如图,弦AB和CD相交于⊙O内一点P,
求证: PA·PB=PC·PD证明:连接AC、BD.∵ ∠A和∠D都是弧BC 所对的圆周角,∴ ∠A=∠D同理 ∠C=∠B∴ △PAC∽△PDB即 PA·PB=PC·PD·ABCDOP例2. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 例题分析解: ∵ DE∥BC,EF∥AB(已知),∴ ∠ADE=∠B=∠EFC (两直线平行,同位角相等)∠AED=∠C. (两直线平行,同位角相等)∴ △ADE∽△EFC. (两个角分别对应相等的两个三角形相似.)例3 已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长.解:∵四边形ABCD为矩形,
∴AD‖BC,∠B=900∴∠DAE=∠AEB∴△AFD∽△EBA又AB=4,AD=5,AE=6例题讲解∵DF⊥AE
∴∠DFA=∠B=900例4,已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC?BC=BE?CD;
(2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.(1)证明:连接EC∵∠BAC,∠BEC都是劣弧BC所对的圆周角∴∠BAC=∠BEC∵CD是△ABC的高∵BE为圆O的直径则∠CDA=∠BCE∴△ACD∽△EBC(2)解:在Rt△CBD中,CD=6,BD=8在Rt△ACD中,CD=6,AD=3∴ AC?BC=BE?CD1. 底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.已知:等腰△ABC AB = AC 和等腰△A'B'C' ,A'B'=A'C'且有∠B=∠B',
求证:△ABC∽△A'B'C'证明:∵等腰三角形 AB=AC ∴∠B=∠C∴△ABC∽△A'B'C' ∵等腰三角形 A'B'=A'C' ∴∠B'=∠C'∵∠B=∠B',∴∠C=∠C' 练 习已知:等腰△ABC 有AB=AC 和 △A'B'C' 有A'B'=A'C', 并且∠A=∠A', 求证:△ABC∽△A'B'C'证明:∵ △ABC中AB=AC,∠B =∠C∴ 2∠B =180°-∠A同理 △A'B'C'中A'B'=A'C',∠B' =∠C'∴ 2∠B' =180°-∠A'又 ∠A=∠A'∵ ∠B=∠B',∵ △ABC∽△A'B'C'2. 如图,Rt△ABC中,CD是斜边上的高,△ACD和△CBD都
和△ABC相似吗?证明你的结论.△ACD∽△ABC△CBD∽△ABC证明:∵∠ACB=∠ADC=90°又∠ A = ∠ A=90°∴ △ACD∽△ABC∵∠CDB=∠ACB=90°∠B = ∠B = 90°∴ △CBD∽△ABC 3 、 已知:如图,A、B、C、D是在同一圆上,弦AB、DC相交于点P。
求证: (1 )∠PCB =∠PAD ;
(2)PA·PB=PC·PD 。4、已知,如图,梯形ABCD中,AD∥BC,
∠A=900,对角线BD⊥CD
试问 1、△ABD与△DCB是什么关系?证明:(1) ∵AD∥BC,
∴ ∠ADB= ∠DBC
∵ ∠A=∠BDC= 90°
∴ △ABD∽△DCB 2、求证: BD2=AD·BC常见
图形相似三角形的识别方法有那些?方法1:通过定义方法5:两角对应相等课 堂 小 结方法2:平行于三角形一边的直线与其它两边
相交,所得三角形与原三角形相似方法3:三边对应比相等方法4:两边对应比相等且夹角相等
(AA)∵DE∥BC ∴△ADE∽△ABC∠A= ∠D△ABC∽△DEF△ABC∽△DEF你有哪些证明三角形相似的方法?(1)我们已学习过哪些判定三角形相似的方法?(3)如(2)题图,△ABC中,点D在AB上,如果∠ACD=∠B,
那么△ACD与△ABC相似吗? 理由:∵AC2=AD?AB又∠A=∠A(2)如图,△ABC中,点D在AB上,如果AC2=AD?AB,那么△ACD与△ABC相似吗?
说说你的理由.相似三角形满足对应角相等,对应边的比相等,那么这两个三角形相似.相似解:相似知识链接∴△ACD∽△ABC平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.如果两个三角形的三组对应边的比相等,那么这两个三角形相似.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似. 观察两副三角尺如图,其中同样角度(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.一般地,如果两个三角形有两组对应角相等,它们一定相似吗?观 察作△ABC和△A‘B’C‘,使得∠A=∠A’,∠B=∠B‘,这时它们的第三个角满足∠C=∠C’吗?分别度量这两个三角形的边长,计算 ,你有什么发现?满足:∠C = ∠C'△ABC∽△A'B'C' 把你的结果与邻座的同学比较,你们的结论一样吗? △ABC和△A'B'C'相似吗?一样△ABC和△A'B'C'相似得到判定两个三角形相似的又一个简便方法:如图,已知△ABC和△A'B'C'中,∠A=∠A', ∠B=∠B',
求证: △ABC∽△A'B'C'证明:在△ABC的边AB(或延长线)上,截取AD=A'B',过点D
作DE//BC,交AC于点E,则有△ADE∽△ABC∵∠ADE=∠B, ∠B=∠B'∴∠ADE=∠B'又∵∠A=∠A',AD=A'B'∴△ADE≌△A'B'C'∴△A'B'C'∽△ABCCC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别(两个角分别对应相等的两个三角形相似)下面每组的两个三角形是否相似?为什么?①①②③④ABCFDEACBDEFBACDFE30o30o30o30o55o30o例1、 如图,弦AB和CD相交于⊙O内一点P,
求证: PA·PB=PC·PD证明:连接AC、BD.∵ ∠A和∠D都是弧BC 所对的圆周角,∴ ∠A=∠D同理 ∠C=∠B∴ △PAC∽△PDB即 PA·PB=PC·PD·ABCDOP例2. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 例题分析解: ∵ DE∥BC,EF∥AB(已知),∴ ∠ADE=∠B=∠EFC (两直线平行,同位角相等)∠AED=∠C. (两直线平行,同位角相等)∴ △ADE∽△EFC. (两个角分别对应相等的两个三角形相似.)例3 已知:如图,矩形ABCD中,E为BC上一点,DF⊥AE于F,若AB=4,AD=5,AE=6,求DF的长.解:∵四边形ABCD为矩形,
∴AD‖BC,∠B=900∴∠DAE=∠AEB∴△AFD∽△EBA又AB=4,AD=5,AE=6例题讲解∵DF⊥AE
∴∠DFA=∠B=900例4,已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC?BC=BE?CD;
(2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.(1)证明:连接EC∵∠BAC,∠BEC都是劣弧BC所对的圆周角∴∠BAC=∠BEC∵CD是△ABC的高∵BE为圆O的直径则∠CDA=∠BCE∴△ACD∽△EBC(2)解:在Rt△CBD中,CD=6,BD=8在Rt△ACD中,CD=6,AD=3∴ AC?BC=BE?CD1. 底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.已知:等腰△ABC AB = AC 和等腰△A'B'C' ,A'B'=A'C'且有∠B=∠B',
求证:△ABC∽△A'B'C'证明:∵等腰三角形 AB=AC ∴∠B=∠C∴△ABC∽△A'B'C' ∵等腰三角形 A'B'=A'C' ∴∠B'=∠C'∵∠B=∠B',∴∠C=∠C' 练 习已知:等腰△ABC 有AB=AC 和 △A'B'C' 有A'B'=A'C', 并且∠A=∠A', 求证:△ABC∽△A'B'C'证明:∵ △ABC中AB=AC,∠B =∠C∴ 2∠B =180°-∠A同理 △A'B'C'中A'B'=A'C',∠B' =∠C'∴ 2∠B' =180°-∠A'又 ∠A=∠A'∵ ∠B=∠B',∵ △ABC∽△A'B'C'2. 如图,Rt△ABC中,CD是斜边上的高,△ACD和△CBD都
和△ABC相似吗?证明你的结论.△ACD∽△ABC△CBD∽△ABC证明:∵∠ACB=∠ADC=90°又∠ A = ∠ A=90°∴ △ACD∽△ABC∵∠CDB=∠ACB=90°∠B = ∠B = 90°∴ △CBD∽△ABC 3 、 已知:如图,A、B、C、D是在同一圆上,弦AB、DC相交于点P。
求证: (1 )∠PCB =∠PAD ;
(2)PA·PB=PC·PD 。4、已知,如图,梯形ABCD中,AD∥BC,
∠A=900,对角线BD⊥CD
试问 1、△ABD与△DCB是什么关系?证明:(1) ∵AD∥BC,
∴ ∠ADB= ∠DBC
∵ ∠A=∠BDC= 90°
∴ △ABD∽△DCB 2、求证: BD2=AD·BC常见
图形相似三角形的识别方法有那些?方法1:通过定义方法5:两角对应相等课 堂 小 结方法2:平行于三角形一边的直线与其它两边
相交,所得三角形与原三角形相似方法3:三边对应比相等方法4:两边对应比相等且夹角相等
