高中数学人教B版(2019)选修第二册高考水平模拟性测试2(Word含解析)
文档属性
| 名称 | 高中数学人教B版(2019)选修第二册高考水平模拟性测试2(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 671.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 11:18:49 | ||
图片预览




文档简介
人教B版(2019) 选修第二册 高考水平模拟性测试卷
一、单选题
1.设随机变量X的可能取值为1,2,…,n,并且取1,2,…,n是等可能的.若,则下面结论中正确的是( )
A. B. C. D.n不能确定
2.已知随机变量的分布列为:
X 1 2 4
P 0.4 0.3 0.3
则等于( )A.15 B.11
C.2.2 D.2.3
3.某市物价部门对5家商场的某商品一天的销售量及其售价进行调查,5家商场的售价(元)和销售量(件)之间的一组数据如表所示.按公式计算,与的回归直线方程是,则下列说法错误的是( )
售价 9 9.5 10 10.5 11
销售量 11 10 8 6 5
A.
B.售价变量每增加1个单位时,销售变量大约减少3.2个单位
C.当时,的估计值为12.8
D.销售量与售价成正相关
4.已知X~N(0,1),则X在区间(-∞,-2)内取值的概率约为( )
A.0.954 B.0.046 C.0.977 D.0.023
5.在某次围棋比赛中,甲、乙两人进入最后决赛.比赛取三局二胜制,即先胜两局的一方获得比赛冠军,比赛结束.假设每局比赛甲胜乙的概率都为,且各局比赛的胜负互不影响,在甲已经先胜一局的情况下,甲获得冠军的概率为( )
A. B. C. D.
6.某班学生考试成绩中,数学不及格的占15%,语文不及格的占5%,两门都不及格的占3%.已知一学生数学不及格,则他语文也不及格的概率是( )
A.0.2 B.0.33 C.0.5 D.0.6
7.电影院一排10个位置,甲、乙、丙三人去看电影,要求他们坐在同一排,且每人左右两边都有空位的坐法种数为( )
A.120 B.80 C.64 D.20
8.在一段时间内,若甲去参观市博物馆的概率为0.8,乙去参观市博物馆的概率为0.6,且甲乙两人各自行动.则在这段时间内,甲乙两人至少有一个去参观博物馆的概率是( )
A.0.48 B.0.32 C.0.92 D.0.84
二、多选题
9.若3男3女排成一排,则下列说法错误的是( )
A.共计有720种不同的排法 B.男生甲排在两端的共有120种排法
C.男生甲、乙相邻的排法总数为120种 D.男女生相间排法总数为72种
10.已知为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,;当两条棱平行时,的值为两条棱之间的距离;当两条棱异面时,.则下列结论正确的是( )
A.共有24对相交棱 B.
C. D.
11.已知,则下列结论正确的是( )
A. B.
C. D.
12.一次抛掷两颗质地均匀的正方体骰子,若出现的点数是2倍关系,则称这次抛掷“漂亮”.规定一次抛掷“漂亮”得分为3,否则得分为-1.若抛掷30次,记累计得分为,则( )
A.抛掷一次,“漂亮”的概率为
B.=2时,“漂亮”的次数必为8
C.E()=-10
D.
三、填空题
13.已知随机变量,,若,则________.
14.已知展开式的各项系数和为64,则所有含“y”的项的系数和为______.
15.某病毒会造成“持续的人传人”,即存在传,又传,又传的传染现象,那么,,就被称为第一代、第二代、第三代传播者.假设一个身体健康的人被第一代、第二代、第三代传播者感染的概率分别为0.9,0.8,0.7.已知健康的小明参加了一次多人宴会,参加宴会的人中有5名第一代传播者,3名第二代传播者,2名第三代传播者,若小明参加宴会仅和感染的10个人中的一个有所接触,则被感染的概率为______.
四、双空题
16.在是否接种疫苗的调查中调查了7人,7人中有4人未接种疫苗,3人接种了疫苗,从这7人中随机抽取3人进行身体检查,用X表示抽取的3人中未接种疫苗的人数,则随机变量X的数学期望为______;设A为事件“抽取的3人中,既有接种疫苗的人,也有未接种疫苗的人”,则事件A发生的概率为______.
五、解答题
17.早在南宋时期,我国数学家杨辉在1261年所著《详解九章算术》一书里,就记载着下表:
这个表称杨辉三角,它比欧洲发现此表的法国数学家帕斯卡至少要早五百年,由此可见,我国古代数学的成就是非常值得我们自豪的.
通过观察杨辉三角数表你能发现它有哪些基本规律?它反映了组合数的哪些基本性质?
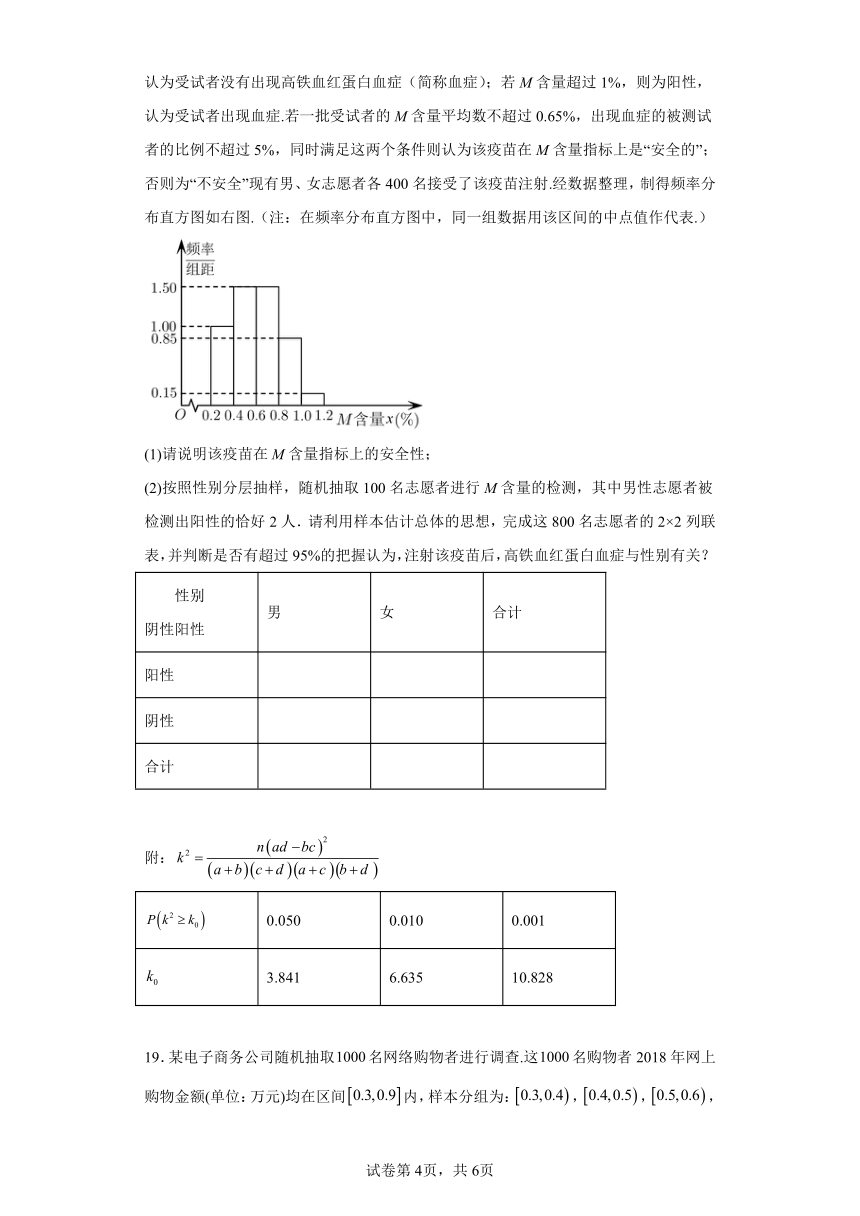
18.某疫苗进行安全性临床试验.该疫苗安全性的一个重要指标是:注射疫苗后人体血液中的高铁血红蛋白(MetHb)的含量(以下简称为“M含量”)不超过1%,则为阴性,认为受试者没有出现高铁血红蛋白血症(简称血症);若M含量超过1%,则为阳性,认为受试者出现血症.若一批受试者的M含量平均数不超过0.65%,出现血症的被测试者的比例不超过5%,同时满足这两个条件则认为该疫苗在M含量指标上是“安全的”;否则为“不安全”现有男、女志愿者各400名接受了该疫苗注射.经数据整理,制得频率分布直方图如右图.(注:在频率分布直方图中,同一组数据用该区间的中点值作代表.)
(1)请说明该疫苗在M含量指标上的安全性;
(2)按照性别分层抽样,随机抽取100名志愿者进行M含量的检测,其中男性志愿者被检测出阳性的恰好2人.请利用样本估计总体的思想,完成这800名志愿者的2×2列联表,并判断是否有超过95%的把握认为,注射该疫苗后,高铁血红蛋白血症与性别有关?
性别 阴性阳性 男 女 合计
阳性
阴性
合计
附:
0.050 0.010 0.001
3.841 6.635 10.828
19.某电子商务公司随机抽取名网络购物者进行调查.这名购物者2018年网上购物金额(单位:万元)均在区间内,样本分组为:,,,,,,购物金额的频率分布直方图如下:
电子商务公司决定给购物者发放优惠券,其金额(单位:元)与购物金额关系如下:
购物金额分组
发放金额 50 100 150 200
(1)求这名购物者获得优惠券金额的平均数;
(2)以这名购物者购物金额落在相应区间的频率作为概率,求一个购物者获得优惠券金额不少于150元的概率.
20.为了检测某种产品的质量,抽取了1个容量为100的样本,数据的分组及各组频数如下表:
分组 频数 频率
3
9
13
16
26
20
7
4
2
合计 100
(1)完成上面的频率分布表;
(2)画出频率直方图;
(3)估计数据落在范围内的可能性.
21.某校高三2班第一小组有男生4人,女生2人,为提高中小学生对劳动教育重要性的认识,现需从中抽取2人参加学校开展的劳动技能学习,学校提供了:除草 翻地 播种 浇水四个项目.规定女生等可能的从中选择1个或者2个项目进行劳动学习,男生等可能的从中选择1个或者2个或者3个项目进行劳动学习,每参加1个劳动项目的学习获得10分,求:
(1)在至少有一名女生参加劳动学习的条件下,恰有一名女生参加劳动学习的概率;
(2)记该小组得分为X,求X的期望.
22.开学在即,某校对全校学生返校所花费的时间进行调查,统计了该校学生居住地到学校的距离x(单位:千米)和学生花费在返校路上的时间y(单位:分钟),得到如下数据:
到学校的距离x(千米) 1.5 2.5 3.4 4.7 5.0 6.9
花费的时间y(分钟) 14 18 24 30 34 42
由统计资料表明y与x具有线性相关关系.
(1)求线性回归方程(精确到0.01);
(2)小明家离学校8千米,请问小明到学校所花费的时间约为多少分钟?(精确出整数)
(3)若的距离数据,称为“完美距离”,那么从6个距离中任取2个,求抽取到的2个数据中至少有一个是“完美距离”的概率.
参考公式及数据:,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
根据题意得,进而得
【详解】
解:随机变量X的可能取值为1,2,…,n,并且取1,2,…,n是等可能的.
所以,解得.
故选:C
2.A
【解析】
【分析】
利用期望的公式求得,根据,即可求解.
【详解】
由随机变量的分布列,可得期望,
所以.
故选:A.
3.D
【解析】
【分析】
首先求出、,再根据回归直线方程必过样本中心点,即可求出,再根据回归直线方程的性质一一判断即可;
【详解】
解:因为,,
与的回归直线方程,恒过定点,
,解得,故A正确,
所以回归直线方程为,即售价变量每增加1个单位时,销售变量大约减少3.2个单位,故B正确;
当时,即当时,的估计值为12.8,故C正确;
因为回归直线方程为,所以销售量与售价成负相关,故D错误;
故选:D
4.D
【解析】
【分析】
根据正态分布曲线的性质求解即可.
【详解】
由题意知,正态曲线的对称轴为x=0,所以P(X<-2)=0.5-P(-2≤X≤2)=0.5-=0.022 8.
故选:D.
5.B
【解析】
【分析】
甲获得冠军有两种情况, 第一种情况:第二局甲获胜获得得比赛冠军, 第二种情况:第二局甲输,第三局甲获胜获胜得比赛冠军,求出两种情况下的概率,相加即可.
【详解】
在甲已经先胜一局的情况下,甲获得冠军有两种情况,
第一种情况:第二局甲获胜获得得比赛冠军,
第二种情况:第二局甲输,第三局甲获胜获胜得比赛冠军,
故甲获得冠军的概率为.
故选:B.
6.A
【解析】
【分析】
【详解】
记“数学不及格”为事件A,“语文不及格”为事件B,P(B|A)===0.2,
所以数学不及格时,该生语文也不及格的概率为0.2.
7.A
【解析】
【分析】
根据题意,先排好7个空座位,注意空座位是相同的,其中6个空位符合条件,将3人插入6个空位中,再对甲、乙、丙三个人进行排列,最后用分步计数原理进行求解即可.
【详解】
解:除甲、乙、丙三人的座位外,还有7个座位,它们之间共可形成六个空,
三人从6个空中选三位置坐上去有种坐法,
而甲、乙、丙三个人进行排列,有种坐法,
所以每人左右两边都有空位的坐法种数为:.
故选:A.
8.C
【解析】
【分析】
根据题意求得甲乙都不去参观博物馆的概率,结合对立事件的概率计算公式,即可求解.
【详解】
由甲去参观市博物馆的概率为0.8,乙去参观市博物馆的概率为0.6,
可得甲乙都不去参观博物馆的概率为,
所以甲乙两人至少有一个去参观博物馆的概率是.
故选:C.
9.BC
【解析】
【分析】
利用全排列、捆绑法、插空法对四种情况进行排列即可解得.
【详解】
3男3女排成一排共计有种;男生甲排在两端的共有种;男生甲、乙相邻的排法总数种;男女生相间排法总数种;
故选:BC
【点睛】
本题考查了全排列、捆绑法、插空法在排列组合中的应用,属于简单题,解题时需要准确选择合理的方法是解题的关键.
10.AC
【解析】
【分析】
根据题设,结合正方体的性质求两条棱相交、平行、异面的可能情况数,再写出对应ξ=0、ξ=1、ξ=的情况数,应用古典概型的概率求法求它们的概率值即可.
【详解】
若两条棱相交,则交点必为正方体8个顶点中的1个,过任意1个顶点恰有3条棱,所以共有对相交棱,因此,故A正确,B错误;
若两条棱平行,则它们的距离为1或,其中距离为的共有6对,故,于是 ,故C正确,D错误.
故选:AC.
11.BC
【解析】
【分析】
分别令,,,求出对应的A,B,C选项,然后再求出展开式中含的项即可求出,由此即可判断.
【详解】
令,则①,故A错误;
令,则,故B正确;
令,则②,
①②可得:,故C正确;
展开式中含的项为,
故,所以D错误,
故选:BC
12.BCD
【解析】
【分析】
利用古典概型概率公式可得抛掷一次,“漂亮”的概率,记抛掷30次抛掷“漂亮”的次数为,则,,即可判断.
【详解】
由题可知一次抛掷两颗质地均匀的正方体骰子有36种等可能的结果,其中出现的点数是2倍关系的有6种等可能的结果,所以抛掷一次,“漂亮”的概率为,故A错误;
记抛掷30次抛掷“漂亮”的次数为,则,,
当时,,即,故B正确;
∴,
∴,故CD正确.
故选:BCD.
13..
【解析】
【分析】
由正态分布可得,然后可得出p的值,再由二项分布的知识可得,进而求出结果.
【详解】
因为,所以,所以,,
又因为,所以.
故答案为:.
14.0
【解析】
【分析】
令,根据题意求得,再令,求得所有不含“y”的项的系数和,即可求得结果.
【详解】
令,,可得,据题意可得,即有;
令,,可得,即所有不含“y”的项的系数和为64,
故可得含“y”的项的系数和为0.
故答案为:.
15.0.83
【解析】
【分析】
设事件“小明与第一代传播者接触”,事件“小明与第二代传播者接触”,事件“小明与第三代传播者接触”,事件“小明被感染”, 则,,,,,,根据全概率公式计算可得答案.
【详解】
解:设事件“小明与第一代传播者接触”,事件“小明与第二代传播者接触”,事件“小明与第三代传播者接触”,事件“小明被感染”,
则,,,,,,
所以.所以所求概率为0.83.
故答案为:0.83.
16.
【解析】
【分析】
分别求出,的概率,进一步求出所以和.
【详解】
由题意可知,随机变量X的取值范围为{0,1,2,3},
,,
,,
所以.
由已知条件可得.
故答案为:;.
17.答案见解析
【解析】
【分析】
根据对称性、且两端为1结合组合数的性质、行列之间的关系、组合数求和等可解.
【详解】
解:杨辉三角用组合数形式数表为
由观察杨辉三角知这张数表有如下基本性质(n,,,):
(1)横行中与首末两端等距离的两个数相等,即;
(2)除1以外的任何一个数都等于它肩上的两个数之和,即;
(3)任何一横行所有数之和等于2的行数的乘方,即;
以上三个性质就是组合数的性质一、性质二和二项式系数总和公式.
(4)同一行上的奇、偶数位上各数之和分别相等,即
(5)n阶杨辉三角共有个数.
(6)n阶杨辉三角所有数之和为:.
(7)杨辉三角第1、3、7、15,…行,即第行(k是正整数)各个数字都是奇数,即(,1,2,…,,)是奇数.
(8)杨辉三角中斜线指示数字和组成一个数列:1,1,2,3,5,8,13,21,34,….
此数列:,,且().
18.(1)答案见解析;
(2)列联表见解析,没有超过95%的把握认为注射疫苗后,高铁血红蛋白血症与性别关.
【解析】
【分析】
(1)求出区间上的频率,以及平均数,即可得出结论;
(2)根据题意填写列联表,计算的值,并与比较大小,即可得出结论.
(1)
由频率分布直方图得,M含量数据落在区间(1.0,1.2]上的频率为0.15×0.2=0.03,
故出现血症的比例为3%<5%,
由直方图得平均数为,
即志愿者的M含量的平均数为0.606%<0.65%,
综上,该疫苗在M含量指标上是“安全的”;
(2)
依题意得,抽取的100名志愿者中男性志愿者应为50人且50名男性志愿者被检测出阳性恰有2人,则全部的男性志愿者中阳性共有人
由(1)知800名志愿者中阳性的频率为0.03,所以阳性的人数共有800×0.03=24人
因此女性志愿者被检测出阳性的人数是24-16=8人.所以完成表格如下:
性别 阴性阳性 男 女 合计
阳性 16 8 24
阴性 384 392 776
合计 400 400 800
则
故由参考数据可得,没有超过95%的把握认为注射疫苗后,高铁血红蛋白血症与性别关.
19.(1);
(2).
【解析】
【分析】
(1)根据频率分布直方图计算名购物者中得元优惠券的人数,再计算平均数即可;
(2)计算购物者2018年网上购物金额位于和的概率之和即可求解.
(1)
名购物者2018年网上消费金额
位于区间的频率为,有人,
位于区间的频率为,有人,
位于区间的频率为,有人
位于区间的频率为,有人
购物者的购物金额与获得优惠券金额的频率分布如下表:
50 100 150 200
频率 0.4 0.3 0.28 0.02
这名购物者获得优惠券金额的平均数为
,
(2)
由题意知:网上消费金额位于和购物者获得优惠券金额不少于150元,
所以购物者获得优惠券金额不少于150元的概率为.
20.(1)频率分布表见解析
(2)频率分布直方图见解析
(3)
【解析】
【分析】
(1)根据题目中进行列表,利用频率=频数/样本容量,求得相应的频率,即可得到分布表;
(2)根据频率/组距,得到频率分布直方图的纵坐标,进而得到频率分布直方图;
(3)根据频率分布表中的数据,即可求得范围内概率,得到答案.
(1)
解:由频率=频数/样本容量,得到频率分布表:
分组 频数 频率
3
9
13
16
26
20
7
4
2
合计 100
(2)
解:由频率分布表中的数据,设每个小矩形的高度分布为:,
可得,,,,,,,,,
所以频率分布直方图,如图所示:
(3)
解:由频率分布直方表中的数据可得:
落在据落在的概率为
所以数据落在范围内的可能性为.
21.(1)
(2)
【解析】
【分析】
(1)设“至少有一名女生参加劳动学习”为事件A,“恰有一名女生参加劳动学习”为事件B.
根据超几何分布原理分别求得,,直接利用条件概率的计算公式即可求得;
(2)设恰有Y人女生参加劳动学习,则男生2-Y人参加劳动学习,求出Y的分布列和数学期望,由即可求出.
(1)
设“至少有一名女生参加劳动学习”为事件A,“恰有一名女生参加劳动学习”为事件B.
根据超几何分布原理得:,
有条件概率的计算公式得:
所以,在至少有一名女生参加劳动学习的条件下,恰有一名女生参加劳动学习的概率为;
(2)
根据题意女生参加劳动学习可获得:(分);
男生参加劳动学习可获得:(分).
设恰有Y人女生参加劳动学习,则男生2-Y人参加劳动学习,则
;;.
所以Y的分布列为:
Y 0 1 2
P
则有:.
又,
∴.
22.(1)
(2)48分钟
(3)
【解析】
【分析】
(1)根据线性回归方程参考公式求出,代入求,即可得出;
(2)代入回归直线方程求解即可;
(3)列出基本事件,根据古典概型概率公式求解.
(1)
,.
∵,,
∴,
将代入,得,
∴.
(2)
当千米,分钟.
∴小明到学校的时间约为48分钟.
(3)
由表格可知,6个数据中的有2个,记作,,剩下的记作B,C,D,E,
则6个数据中抽取2个数据共有15种,
即,,,,,,,,,BC,BD,BE,CD,CE,DE.
其中至少有一个完美距离的有9种,
所以抽取到至少有一个是“完美距离”的概率.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.设随机变量X的可能取值为1,2,…,n,并且取1,2,…,n是等可能的.若,则下面结论中正确的是( )
A. B. C. D.n不能确定
2.已知随机变量的分布列为:
X 1 2 4
P 0.4 0.3 0.3
则等于( )A.15 B.11
C.2.2 D.2.3
3.某市物价部门对5家商场的某商品一天的销售量及其售价进行调查,5家商场的售价(元)和销售量(件)之间的一组数据如表所示.按公式计算,与的回归直线方程是,则下列说法错误的是( )
售价 9 9.5 10 10.5 11
销售量 11 10 8 6 5
A.
B.售价变量每增加1个单位时,销售变量大约减少3.2个单位
C.当时,的估计值为12.8
D.销售量与售价成正相关
4.已知X~N(0,1),则X在区间(-∞,-2)内取值的概率约为( )
A.0.954 B.0.046 C.0.977 D.0.023
5.在某次围棋比赛中,甲、乙两人进入最后决赛.比赛取三局二胜制,即先胜两局的一方获得比赛冠军,比赛结束.假设每局比赛甲胜乙的概率都为,且各局比赛的胜负互不影响,在甲已经先胜一局的情况下,甲获得冠军的概率为( )
A. B. C. D.
6.某班学生考试成绩中,数学不及格的占15%,语文不及格的占5%,两门都不及格的占3%.已知一学生数学不及格,则他语文也不及格的概率是( )
A.0.2 B.0.33 C.0.5 D.0.6
7.电影院一排10个位置,甲、乙、丙三人去看电影,要求他们坐在同一排,且每人左右两边都有空位的坐法种数为( )
A.120 B.80 C.64 D.20
8.在一段时间内,若甲去参观市博物馆的概率为0.8,乙去参观市博物馆的概率为0.6,且甲乙两人各自行动.则在这段时间内,甲乙两人至少有一个去参观博物馆的概率是( )
A.0.48 B.0.32 C.0.92 D.0.84
二、多选题
9.若3男3女排成一排,则下列说法错误的是( )
A.共计有720种不同的排法 B.男生甲排在两端的共有120种排法
C.男生甲、乙相邻的排法总数为120种 D.男女生相间排法总数为72种
10.已知为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,;当两条棱平行时,的值为两条棱之间的距离;当两条棱异面时,.则下列结论正确的是( )
A.共有24对相交棱 B.
C. D.
11.已知,则下列结论正确的是( )
A. B.
C. D.
12.一次抛掷两颗质地均匀的正方体骰子,若出现的点数是2倍关系,则称这次抛掷“漂亮”.规定一次抛掷“漂亮”得分为3,否则得分为-1.若抛掷30次,记累计得分为,则( )
A.抛掷一次,“漂亮”的概率为
B.=2时,“漂亮”的次数必为8
C.E()=-10
D.
三、填空题
13.已知随机变量,,若,则________.
14.已知展开式的各项系数和为64,则所有含“y”的项的系数和为______.
15.某病毒会造成“持续的人传人”,即存在传,又传,又传的传染现象,那么,,就被称为第一代、第二代、第三代传播者.假设一个身体健康的人被第一代、第二代、第三代传播者感染的概率分别为0.9,0.8,0.7.已知健康的小明参加了一次多人宴会,参加宴会的人中有5名第一代传播者,3名第二代传播者,2名第三代传播者,若小明参加宴会仅和感染的10个人中的一个有所接触,则被感染的概率为______.
四、双空题
16.在是否接种疫苗的调查中调查了7人,7人中有4人未接种疫苗,3人接种了疫苗,从这7人中随机抽取3人进行身体检查,用X表示抽取的3人中未接种疫苗的人数,则随机变量X的数学期望为______;设A为事件“抽取的3人中,既有接种疫苗的人,也有未接种疫苗的人”,则事件A发生的概率为______.
五、解答题
17.早在南宋时期,我国数学家杨辉在1261年所著《详解九章算术》一书里,就记载着下表:
这个表称杨辉三角,它比欧洲发现此表的法国数学家帕斯卡至少要早五百年,由此可见,我国古代数学的成就是非常值得我们自豪的.
通过观察杨辉三角数表你能发现它有哪些基本规律?它反映了组合数的哪些基本性质?
18.某疫苗进行安全性临床试验.该疫苗安全性的一个重要指标是:注射疫苗后人体血液中的高铁血红蛋白(MetHb)的含量(以下简称为“M含量”)不超过1%,则为阴性,认为受试者没有出现高铁血红蛋白血症(简称血症);若M含量超过1%,则为阳性,认为受试者出现血症.若一批受试者的M含量平均数不超过0.65%,出现血症的被测试者的比例不超过5%,同时满足这两个条件则认为该疫苗在M含量指标上是“安全的”;否则为“不安全”现有男、女志愿者各400名接受了该疫苗注射.经数据整理,制得频率分布直方图如右图.(注:在频率分布直方图中,同一组数据用该区间的中点值作代表.)
(1)请说明该疫苗在M含量指标上的安全性;
(2)按照性别分层抽样,随机抽取100名志愿者进行M含量的检测,其中男性志愿者被检测出阳性的恰好2人.请利用样本估计总体的思想,完成这800名志愿者的2×2列联表,并判断是否有超过95%的把握认为,注射该疫苗后,高铁血红蛋白血症与性别有关?
性别 阴性阳性 男 女 合计
阳性
阴性
合计
附:
0.050 0.010 0.001
3.841 6.635 10.828
19.某电子商务公司随机抽取名网络购物者进行调查.这名购物者2018年网上购物金额(单位:万元)均在区间内,样本分组为:,,,,,,购物金额的频率分布直方图如下:
电子商务公司决定给购物者发放优惠券,其金额(单位:元)与购物金额关系如下:
购物金额分组
发放金额 50 100 150 200
(1)求这名购物者获得优惠券金额的平均数;
(2)以这名购物者购物金额落在相应区间的频率作为概率,求一个购物者获得优惠券金额不少于150元的概率.
20.为了检测某种产品的质量,抽取了1个容量为100的样本,数据的分组及各组频数如下表:
分组 频数 频率
3
9
13
16
26
20
7
4
2
合计 100
(1)完成上面的频率分布表;
(2)画出频率直方图;
(3)估计数据落在范围内的可能性.
21.某校高三2班第一小组有男生4人,女生2人,为提高中小学生对劳动教育重要性的认识,现需从中抽取2人参加学校开展的劳动技能学习,学校提供了:除草 翻地 播种 浇水四个项目.规定女生等可能的从中选择1个或者2个项目进行劳动学习,男生等可能的从中选择1个或者2个或者3个项目进行劳动学习,每参加1个劳动项目的学习获得10分,求:
(1)在至少有一名女生参加劳动学习的条件下,恰有一名女生参加劳动学习的概率;
(2)记该小组得分为X,求X的期望.
22.开学在即,某校对全校学生返校所花费的时间进行调查,统计了该校学生居住地到学校的距离x(单位:千米)和学生花费在返校路上的时间y(单位:分钟),得到如下数据:
到学校的距离x(千米) 1.5 2.5 3.4 4.7 5.0 6.9
花费的时间y(分钟) 14 18 24 30 34 42
由统计资料表明y与x具有线性相关关系.
(1)求线性回归方程(精确到0.01);
(2)小明家离学校8千米,请问小明到学校所花费的时间约为多少分钟?(精确出整数)
(3)若的距离数据,称为“完美距离”,那么从6个距离中任取2个,求抽取到的2个数据中至少有一个是“完美距离”的概率.
参考公式及数据:,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
根据题意得,进而得
【详解】
解:随机变量X的可能取值为1,2,…,n,并且取1,2,…,n是等可能的.
所以,解得.
故选:C
2.A
【解析】
【分析】
利用期望的公式求得,根据,即可求解.
【详解】
由随机变量的分布列,可得期望,
所以.
故选:A.
3.D
【解析】
【分析】
首先求出、,再根据回归直线方程必过样本中心点,即可求出,再根据回归直线方程的性质一一判断即可;
【详解】
解:因为,,
与的回归直线方程,恒过定点,
,解得,故A正确,
所以回归直线方程为,即售价变量每增加1个单位时,销售变量大约减少3.2个单位,故B正确;
当时,即当时,的估计值为12.8,故C正确;
因为回归直线方程为,所以销售量与售价成负相关,故D错误;
故选:D
4.D
【解析】
【分析】
根据正态分布曲线的性质求解即可.
【详解】
由题意知,正态曲线的对称轴为x=0,所以P(X<-2)=0.5-P(-2≤X≤2)=0.5-=0.022 8.
故选:D.
5.B
【解析】
【分析】
甲获得冠军有两种情况, 第一种情况:第二局甲获胜获得得比赛冠军, 第二种情况:第二局甲输,第三局甲获胜获胜得比赛冠军,求出两种情况下的概率,相加即可.
【详解】
在甲已经先胜一局的情况下,甲获得冠军有两种情况,
第一种情况:第二局甲获胜获得得比赛冠军,
第二种情况:第二局甲输,第三局甲获胜获胜得比赛冠军,
故甲获得冠军的概率为.
故选:B.
6.A
【解析】
【分析】
【详解】
记“数学不及格”为事件A,“语文不及格”为事件B,P(B|A)===0.2,
所以数学不及格时,该生语文也不及格的概率为0.2.
7.A
【解析】
【分析】
根据题意,先排好7个空座位,注意空座位是相同的,其中6个空位符合条件,将3人插入6个空位中,再对甲、乙、丙三个人进行排列,最后用分步计数原理进行求解即可.
【详解】
解:除甲、乙、丙三人的座位外,还有7个座位,它们之间共可形成六个空,
三人从6个空中选三位置坐上去有种坐法,
而甲、乙、丙三个人进行排列,有种坐法,
所以每人左右两边都有空位的坐法种数为:.
故选:A.
8.C
【解析】
【分析】
根据题意求得甲乙都不去参观博物馆的概率,结合对立事件的概率计算公式,即可求解.
【详解】
由甲去参观市博物馆的概率为0.8,乙去参观市博物馆的概率为0.6,
可得甲乙都不去参观博物馆的概率为,
所以甲乙两人至少有一个去参观博物馆的概率是.
故选:C.
9.BC
【解析】
【分析】
利用全排列、捆绑法、插空法对四种情况进行排列即可解得.
【详解】
3男3女排成一排共计有种;男生甲排在两端的共有种;男生甲、乙相邻的排法总数种;男女生相间排法总数种;
故选:BC
【点睛】
本题考查了全排列、捆绑法、插空法在排列组合中的应用,属于简单题,解题时需要准确选择合理的方法是解题的关键.
10.AC
【解析】
【分析】
根据题设,结合正方体的性质求两条棱相交、平行、异面的可能情况数,再写出对应ξ=0、ξ=1、ξ=的情况数,应用古典概型的概率求法求它们的概率值即可.
【详解】
若两条棱相交,则交点必为正方体8个顶点中的1个,过任意1个顶点恰有3条棱,所以共有对相交棱,因此,故A正确,B错误;
若两条棱平行,则它们的距离为1或,其中距离为的共有6对,故,于是 ,故C正确,D错误.
故选:AC.
11.BC
【解析】
【分析】
分别令,,,求出对应的A,B,C选项,然后再求出展开式中含的项即可求出,由此即可判断.
【详解】
令,则①,故A错误;
令,则,故B正确;
令,则②,
①②可得:,故C正确;
展开式中含的项为,
故,所以D错误,
故选:BC
12.BCD
【解析】
【分析】
利用古典概型概率公式可得抛掷一次,“漂亮”的概率,记抛掷30次抛掷“漂亮”的次数为,则,,即可判断.
【详解】
由题可知一次抛掷两颗质地均匀的正方体骰子有36种等可能的结果,其中出现的点数是2倍关系的有6种等可能的结果,所以抛掷一次,“漂亮”的概率为,故A错误;
记抛掷30次抛掷“漂亮”的次数为,则,,
当时,,即,故B正确;
∴,
∴,故CD正确.
故选:BCD.
13..
【解析】
【分析】
由正态分布可得,然后可得出p的值,再由二项分布的知识可得,进而求出结果.
【详解】
因为,所以,所以,,
又因为,所以.
故答案为:.
14.0
【解析】
【分析】
令,根据题意求得,再令,求得所有不含“y”的项的系数和,即可求得结果.
【详解】
令,,可得,据题意可得,即有;
令,,可得,即所有不含“y”的项的系数和为64,
故可得含“y”的项的系数和为0.
故答案为:.
15.0.83
【解析】
【分析】
设事件“小明与第一代传播者接触”,事件“小明与第二代传播者接触”,事件“小明与第三代传播者接触”,事件“小明被感染”, 则,,,,,,根据全概率公式计算可得答案.
【详解】
解:设事件“小明与第一代传播者接触”,事件“小明与第二代传播者接触”,事件“小明与第三代传播者接触”,事件“小明被感染”,
则,,,,,,
所以.所以所求概率为0.83.
故答案为:0.83.
16.
【解析】
【分析】
分别求出,的概率,进一步求出所以和.
【详解】
由题意可知,随机变量X的取值范围为{0,1,2,3},
,,
,,
所以.
由已知条件可得.
故答案为:;.
17.答案见解析
【解析】
【分析】
根据对称性、且两端为1结合组合数的性质、行列之间的关系、组合数求和等可解.
【详解】
解:杨辉三角用组合数形式数表为
由观察杨辉三角知这张数表有如下基本性质(n,,,):
(1)横行中与首末两端等距离的两个数相等,即;
(2)除1以外的任何一个数都等于它肩上的两个数之和,即;
(3)任何一横行所有数之和等于2的行数的乘方,即;
以上三个性质就是组合数的性质一、性质二和二项式系数总和公式.
(4)同一行上的奇、偶数位上各数之和分别相等,即
(5)n阶杨辉三角共有个数.
(6)n阶杨辉三角所有数之和为:.
(7)杨辉三角第1、3、7、15,…行,即第行(k是正整数)各个数字都是奇数,即(,1,2,…,,)是奇数.
(8)杨辉三角中斜线指示数字和组成一个数列:1,1,2,3,5,8,13,21,34,….
此数列:,,且().
18.(1)答案见解析;
(2)列联表见解析,没有超过95%的把握认为注射疫苗后,高铁血红蛋白血症与性别关.
【解析】
【分析】
(1)求出区间上的频率,以及平均数,即可得出结论;
(2)根据题意填写列联表,计算的值,并与比较大小,即可得出结论.
(1)
由频率分布直方图得,M含量数据落在区间(1.0,1.2]上的频率为0.15×0.2=0.03,
故出现血症的比例为3%<5%,
由直方图得平均数为,
即志愿者的M含量的平均数为0.606%<0.65%,
综上,该疫苗在M含量指标上是“安全的”;
(2)
依题意得,抽取的100名志愿者中男性志愿者应为50人且50名男性志愿者被检测出阳性恰有2人,则全部的男性志愿者中阳性共有人
由(1)知800名志愿者中阳性的频率为0.03,所以阳性的人数共有800×0.03=24人
因此女性志愿者被检测出阳性的人数是24-16=8人.所以完成表格如下:
性别 阴性阳性 男 女 合计
阳性 16 8 24
阴性 384 392 776
合计 400 400 800
则
故由参考数据可得,没有超过95%的把握认为注射疫苗后,高铁血红蛋白血症与性别关.
19.(1);
(2).
【解析】
【分析】
(1)根据频率分布直方图计算名购物者中得元优惠券的人数,再计算平均数即可;
(2)计算购物者2018年网上购物金额位于和的概率之和即可求解.
(1)
名购物者2018年网上消费金额
位于区间的频率为,有人,
位于区间的频率为,有人,
位于区间的频率为,有人
位于区间的频率为,有人
购物者的购物金额与获得优惠券金额的频率分布如下表:
50 100 150 200
频率 0.4 0.3 0.28 0.02
这名购物者获得优惠券金额的平均数为
,
(2)
由题意知:网上消费金额位于和购物者获得优惠券金额不少于150元,
所以购物者获得优惠券金额不少于150元的概率为.
20.(1)频率分布表见解析
(2)频率分布直方图见解析
(3)
【解析】
【分析】
(1)根据题目中进行列表,利用频率=频数/样本容量,求得相应的频率,即可得到分布表;
(2)根据频率/组距,得到频率分布直方图的纵坐标,进而得到频率分布直方图;
(3)根据频率分布表中的数据,即可求得范围内概率,得到答案.
(1)
解:由频率=频数/样本容量,得到频率分布表:
分组 频数 频率
3
9
13
16
26
20
7
4
2
合计 100
(2)
解:由频率分布表中的数据,设每个小矩形的高度分布为:,
可得,,,,,,,,,
所以频率分布直方图,如图所示:
(3)
解:由频率分布直方表中的数据可得:
落在据落在的概率为
所以数据落在范围内的可能性为.
21.(1)
(2)
【解析】
【分析】
(1)设“至少有一名女生参加劳动学习”为事件A,“恰有一名女生参加劳动学习”为事件B.
根据超几何分布原理分别求得,,直接利用条件概率的计算公式即可求得;
(2)设恰有Y人女生参加劳动学习,则男生2-Y人参加劳动学习,求出Y的分布列和数学期望,由即可求出.
(1)
设“至少有一名女生参加劳动学习”为事件A,“恰有一名女生参加劳动学习”为事件B.
根据超几何分布原理得:,
有条件概率的计算公式得:
所以,在至少有一名女生参加劳动学习的条件下,恰有一名女生参加劳动学习的概率为;
(2)
根据题意女生参加劳动学习可获得:(分);
男生参加劳动学习可获得:(分).
设恰有Y人女生参加劳动学习,则男生2-Y人参加劳动学习,则
;;.
所以Y的分布列为:
Y 0 1 2
P
则有:.
又,
∴.
22.(1)
(2)48分钟
(3)
【解析】
【分析】
(1)根据线性回归方程参考公式求出,代入求,即可得出;
(2)代入回归直线方程求解即可;
(3)列出基本事件,根据古典概型概率公式求解.
(1)
,.
∵,,
∴,
将代入,得,
∴.
(2)
当千米,分钟.
∴小明到学校的时间约为48分钟.
(3)
由表格可知,6个数据中的有2个,记作,,剩下的记作B,C,D,E,
则6个数据中抽取2个数据共有15种,
即,,,,,,,,,BC,BD,BE,CD,CE,DE.
其中至少有一个完美距离的有9种,
所以抽取到至少有一个是“完美距离”的概率.
答案第1页,共2页
答案第1页,共2页
