高中数学人教B版(2019)选修第二册高考水平模拟性测试4(Word含解析)
文档属性
| 名称 | 高中数学人教B版(2019)选修第二册高考水平模拟性测试4(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 700.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 11:21:17 | ||
图片预览



文档简介
人教B版(2019) 选修第二册 高考水平模拟性测试卷
一、单选题
1.已知随机变量X的分布列如表所示,则( )
X 1 2 3
P a 2a 3a
A. B. C. D.
2.已知随机变量的分布列如下:
若随机变量,则为( )A. B. C. D.随变化而变化
3.新能源汽车是指采用非常规的车用燃料作为动力来源(或使用常规的车用燃料、采用新型车载动力装置),综合车辆的动力控制和驱动方面的先进技术,形成的技术原理先进、具有新技术、新结构的汽车.新能源汽车包括混合动力电动汽车(HEV)、纯电动汽车(BEV,包括太阳能汽车)、燃料电池电动汽车(FCEV)、其他新能源(如超级电容器、飞轮等高效储能器)汽车等.非常规的车用燃料指除汽油、柴油之外的燃料.下表是2021年我国某地区新能源汽车的前5个月销售量与月份的统计表:
月份代码x 1 2 3 4 5
销售量y(万辆) 0.5 0.6 1 1.4 1.5
由上表可知其线性回归方程为,则的值是( ).A.0.28 B.0.32 C.0.56 D.0.64
4.已知随机变量X服从正态分布,且,则( )
A.0.1 B.0.2 C.0.3 D.0.4
5.有甲、乙、丙三个工厂生产同一型号的产品,甲厂生产的次品率为,乙厂生产的次品率为,丙厂生产的次品率为,生产出来的产品混放在一起.已知甲、乙、丙三个工厂生产的产品数分别占总数的、、,任取一件产品,则取得产品为次品的概率是( )
A. B. C. D.
6.某种元件的使用寿命超过1年的概率为0.6,使用寿命超过2年的概率为0.3,则已经使用了1年的元件,使用寿命超过2年的概率为( )
A.0.3 B.0.5 C.0.6 D.1
7.当前,新冠肺炎疫情进入常态化防控新阶段,防止疫情输入的任务依然繁重,疫情防控工作形势依然严峻、复杂.某地区安排A,B,C,D,E五名同志到三个地区开展防疫宣传活动,每个地区至少安排一人,且A,B两人安排在同一个地区,C,D两人不安排在同一个地区,则不同的分配方法总数为( )
A.30种 B.36种 C.42种 D.64种
8.在一段时间内,若甲去参观市博物馆的概率为0.8,乙去参观市博物馆的概率为0.6,且甲乙两人各自行动.则在这段时间内,甲乙两人至少有一个去参观博物馆的概率是( )
A.0.48 B.0.32 C.0.92 D.0.84
二、多选题
9.(多选题)A、B、C、D、E五个人并排站在一起,则下列说法正确的有( )
A.若A、B不相邻共有72种方法
B.若A不站在最左边,B不站最右边,有78种方法.
C.若A在B左边有60种排法
D.若A、B两人站在一起有24种方法
10.已知甲盒中仅有1个球且为红球,乙盒中有个红球和个蓝球(,,,),从乙盒中随机抽取个球放入甲盒中.
①放入个球后,甲盒中含有红球的个数记为
②放入个球后,从甲盒中取1个球是红球的概率记为.则()
A. B.
C. D.
11.若,则下列结论正确的是( )
A.若,、为整数,则
B.是正整数
C.是的小数部分
D.设,若、为整数,则
12.某人有6把钥匙,其中n把能打开门.如果随机地取一把钥匙试着开门,把不能开门的钥匙扔掉,设第二次才能打开门的概率为p,则下列结论正确的是( )
A.当时, B.当时,
C.当时, D.当时,
三、填空题
13.投掷两枚骰子,当至少一枚5点或一枚6点出现时,就说这次试验成功,则在10次试验中成功次数的均值为________.
14.在的展开式中,二项式系数之和与各项系数之和比为1:32,则的系数为___________.
15.有三个箱子,分别编号为、、.号箱装有个红球、个白球,号箱装有个红球、个白球,号箱装有个红球.某人从三个箱子中任取一箱,从中任意摸出一球,取得红球的概率为________.
四、双空题
16.在是否接种疫苗的调查中调查了7人,7人中有4人未接种疫苗,3人接种了疫苗,从这7人中随机抽取3人进行身体检查,用X表示抽取的3人中未接种疫苗的人数,则随机变量X的数学期望为______;设A为事件“抽取的3人中,既有接种疫苗的人,也有未接种疫苗的人”,则事件A发生的概率为______.
五、解答题
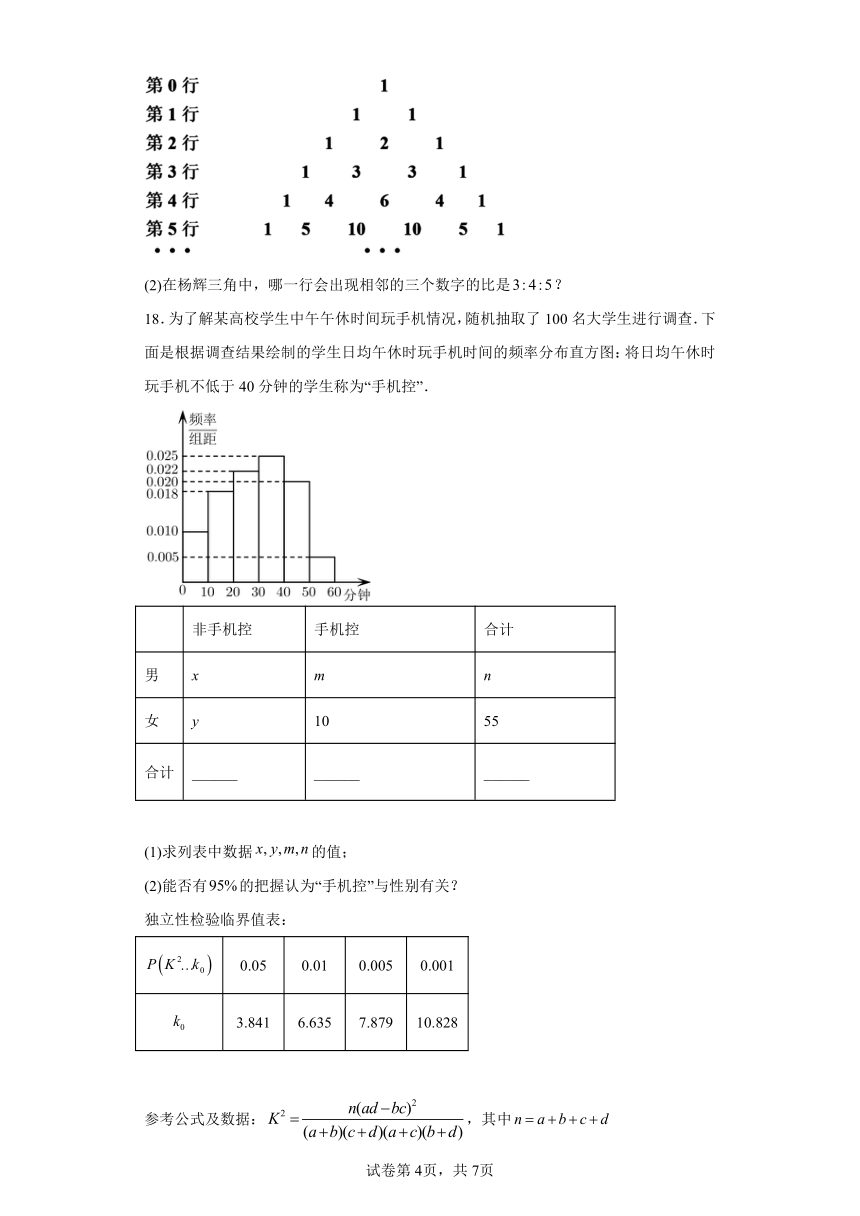
17.在杨辉三角中,除每行的两端数字外,每个数字都等于它左上角和右上角两个数字之和,杨辉三角开头几行如图所示.
(1)利用杨辉三角展开
(2)在杨辉三角中,哪一行会出现相邻的三个数字的比是?
18.为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时玩手机时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.
非手机控 手机控 合计
男 x m n
女 y 10 55
合计 ______ ______ ______
(1)求列表中数据的值;
(2)能否有的把握认为“手机控”与性别有关?
独立性检验临界值表:
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
参考公式及数据:,其中
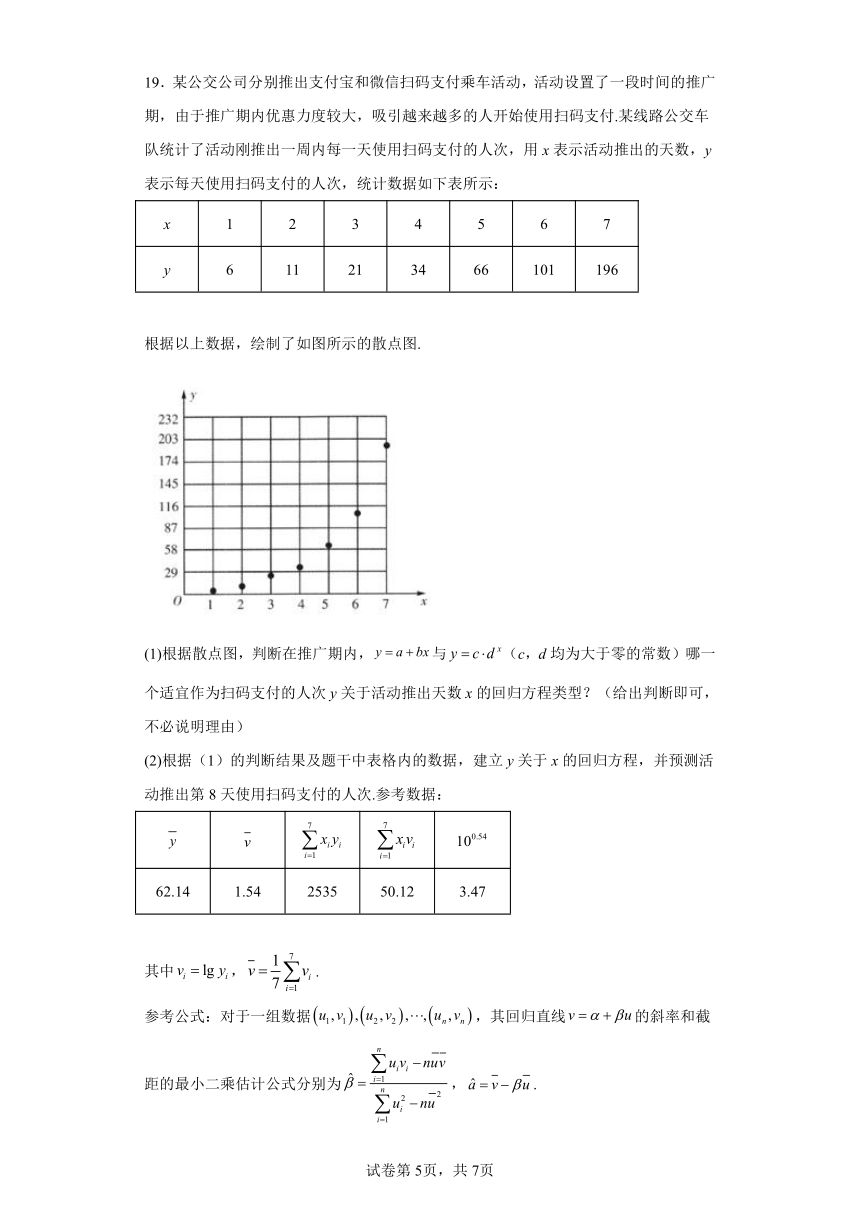
19.某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次,统计数据如下表所示:
x 1 2 3 4 5 6 7
y 6 11 21 34 66 101 196
根据以上数据,绘制了如图所示的散点图.
(1)根据散点图,判断在推广期内,与(c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及题干中表格内的数据,建立y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次.参考数据:
62.14 1.54 2535 50.12 3.47
其中,.
参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计公式分别为,.
(3)推广期结束后,为更好地服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
支付方式 现金 公交卡 扫码
人次 10 60 30
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用公交卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调查结果发现:使用扫码支付的乘客中有5人次乘客享受7折优惠,有10人次乘客享受8折优惠,有15人次乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
20.为了检测某种产品的质量,抽取了1个容量为100的样本,数据的分组及各组频数如下表:
分组 频数 频率
3
9
13
16
26
20
7
4
2
合计 100
(1)完成上面的频率分布表;
(2)画出频率直方图;
(3)估计数据落在范围内的可能性.
21.某校高三2班第一小组有男生4人,女生2人,为提高中小学生对劳动教育重要性的认识,现需从中抽取2人参加学校开展的劳动技能学习,学校提供了:除草 翻地 播种 浇水四个项目.规定女生等可能的从中选择1个或者2个项目进行劳动学习,男生等可能的从中选择1个或者2个或者3个项目进行劳动学习,每参加1个劳动项目的学习获得10分,求:
(1)在至少有一名女生参加劳动学习的条件下,恰有一名女生参加劳动学习的概率;
(2)记该小组得分为X,求X的期望.
22.近年来,国民经济的增长和社会结构的变化推动宠物饲养成为很多人精神消费的主要方式,使得近几年中国宠物市场规模逐年增长,下表为2016~2020年中国宠物市场规模y(单位:千亿元),其中2016~2020年对应的年份代码x依次为1~5.
年份代码x 1 2 3 4 5
宠物市场规模y/千亿元 1.22 1.34 1.78 2.21 2.95
(1)由表中数据可知,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)求y关于x的线性回归方程,并预测2022年中国宠物市场规模.
参考数据:,,,.
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
根据分布列的性质计算可得;
【详解】
解:依题意,解得,所以;
故选:C
2.C
【解析】
【分析】
先根据概率之和为1,求得m,再求得,然后利用期望性质求解.
【详解】
因为,
所以,
所以.
又,
所以.
故选:C
3.A
【解析】
【分析】
先计算,,再根据样本中心点适合方程解得的值即可.
【详解】
由表中数据可得,,
将代入,即,解得.
故选:A.
4.D
【解析】
【分析】
利用正态曲线的对称性进行求解.
【详解】
因为随机变量X服从正态分布,
所以正态曲线关于直线对称,
又,
所以,
则.
故选:D.
5.D
【解析】
【分析】
根据三个工厂生产的产品数的占比以及次品率可求得结果.
【详解】
由题意可知,任取一件产品,则取得产品为次品的概率是.
故选:D.
6.B
【解析】
【分析】
利用条件概率的计算公式进行求解.
【详解】
设事件A为“该元件的使用寿命超过1年”,B为“该元件的使用寿命超过2年”,则,.因为,所以,
所以.
故选:B.
7.A
【解析】
【分析】
由题意可得,分两个地区各分2人,另一个地区分1人和两个地区各分1人,另一个地区分3人两种情况,对两种情况的种数求和,即可求解.
【详解】
解:①当两个地区各分2人,另一个地区分1人时,总数有种;
②当两个地区各分1人,另一个地区分3人时,总数有种.
故满足条件的分法共有种.
故选:A
8.C
【解析】
【分析】
根据题意求得甲乙都不去参观博物馆的概率,结合对立事件的概率计算公式,即可求解.
【详解】
由甲去参观市博物馆的概率为0.8,乙去参观市博物馆的概率为0.6,
可得甲乙都不去参观博物馆的概率为,
所以甲乙两人至少有一个去参观博物馆的概率是.
故选:C.
9.ABC
【解析】
【分析】
利用插空法,可判断A的正误;利用间接法,可判断B的正误;根据定序问题的求法,可判断C的正误;利用捆绑法,可判断D的正误,即可得答案.
【详解】
对于A:若A、B不相邻共有种方法,故A正确;
对于B:若A不站在最左边,B不站最右边,利用间接法有种方法,故B正确;
对于C:若A在B左边有种方法,故C正确;
对于D:若A、B两人站在一起有,故D不正确.
故选:ABC
10.AD
【解析】
【分析】
求得随机变量,的分布列,根据数学期望公式计算可得选项.
【详解】
解:因为,,所以随机变量的分布列为:
1 2
因为,,,所以随机变量的分布列为:
1 2 3
所以,,所以.
因为,,所以,所以.
故选:AD.
11.ACD
【解析】
【分析】
求出、,可判断A的正误;取可判断B的正误;利用二项式定理可判断C的正误;分为偶数和为奇数两种情况分析讨论,结合二项式定理可判断D的正误.
【详解】
对于A,,
所以,,,则,A对;
对于B,,
因为,不是正整数,B错;
对于C,因为
是正整数,
而,所以是的小数部分,C对;
对于D,因为,
当为偶数时,,
,
所以
,
所以,
即;
当为奇数时,,
,
所以
,
所以,
即,D对.
故选:ACD.
12.AC
【解析】
【分析】
根据不同的取值,分别计算对应概率求解.
【详解】
当时,,选项A正确;
当时,,选项B错误;
当时,,选项C正确;
当时,,选项D错误.
故选:AC
13.
【解析】
【分析】
先利用古典概型求得试验成功的概率,再利用二项分布均值公式求解.
【详解】
在投掷两枚骰子中,不含5或6的次数为4×4,
故试验成功的概率P=1-=,
则在10次试验中成功次数的均值E(ξ)=.
故答案为:
14.90
【解析】
【分析】
根据二项式系数的性质求得n的值,再利用二项展开式的通项公式,求得的系数.
【详解】
令,则,所以的展开式中,各项系数和为,
又二项式系数和为,所以,解得.
二项展开式的通项,令,得,
所以的系数为,
故答案为:.
15.
【解析】
【分析】
记事件为“球取自于号箱”,记事件为“取得红球”,可得出,结合全概率公式可求得结果.
【详解】
记事件为“球取自于号箱”,记事件为“取得红球”,
发生总是伴随着、、之一同时发生,即,
且、、两两互斥,
,,,,
所以,
.
故答案为:.
【点睛】
关键点点睛:本题考查利用全概率公式计算事件的概率,解题的关键在于球取自于几号袋,再结合全概率公式进行计算.
16.
【解析】
【分析】
分别求出,的概率,进一步求出所以和.
【详解】
由题意可知,随机变量X的取值范围为{0,1,2,3},
,,
,,
所以.
由已知条件可得.
故答案为:;.
17.(1)
(2)第62行会出现相邻的三个数字的比是
【解析】
【分析】
(1)根据题意得,再令,即可得答案;
(2)设在第n行出现的三个相邻的数的比是,并设这三个数分别是,,,进而根据比值关系解方程即可得答案.
(1)
解:根据杨辉三角的规律“每行两端都是1,其余每个数都等于它左上角和右上角两个数字的和”,可写出第6行的二项式系数为1,6,15,20,15,6,1,
所以.
令,,得.
(2)
解:设在第n行出现的三个相邻的数的比是,并设这三个数分别是,,,则有
所以
所以即所以
即在第62行会出现相邻的三个数字的比是.
18.(1)x=30,y=45,m=15,n=45
(2)没有95%把握认为“手机控”与性别有关
【解析】
【分析】
(1)由频率分布直方图,求出在抽取的100人中“手机控”的人数即可求解;
(2)求出2×2列联表,根据参考公式求出K2,由临界值表即可判断.
(1)
解:由频率分布直方图可知,在抽取的100人中,“手机控”有:100×(0.2+0.05)=25人,非手机控75人,
∴x=30,y=45,m=15,n=45;
(2)
解:由(1)可得2×2列联表如下:
非手机控 手机控 合计
男 30 15 45
女 45 10 55
合计 75 25 100
所以K2=≈3.030<3.841,
所以没有95%把握认为“手机控”与性别有关.
19.(1)适宜
(2),活动推出第8天使用扫码支付的人次为347
(3)199200元
【解析】
【分析】
(1)根据散点图即可判断回归方程类型;
(2)根据题意中的数据,利用最小二乘法求出,进而求出,即可得出回归方程,令求解即可;
(3)根据题意分别求出享受7折优惠、8折优惠、9折优惠的收入,进而加起来即可.
(1)
根据散点图判断,适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型.
(2)
∵,∴两边同时取常用对数,得.
设,,则.
∵,,,
∴,
,∴,∴,
把代入上式,得,
∴y关于x的回归方程为,活动推出第8天使用扫码支付的人次为347.
(3)
由题意,可知一个月中使用现金的乘客有1000人次,共收入(元);
使用公交卡的乘客有6000人次,共收入(元).
使用扫码支付的乘客有3000人次,
其中,享受7折优惠的有500人次,共收入(元),
享受8折优惠的有1000人次,共收入(元),
享受9折优惠的有1500人次,共收入(元),
故该车队一辆车一个月的收入为(元).
∴估计该车队一辆车一年的收入为(元).
20.(1)频率分布表见解析
(2)频率分布直方图见解析
(3)
【解析】
【分析】
(1)根据题目中进行列表,利用频率=频数/样本容量,求得相应的频率,即可得到分布表;
(2)根据频率/组距,得到频率分布直方图的纵坐标,进而得到频率分布直方图;
(3)根据频率分布表中的数据,即可求得范围内概率,得到答案.
(1)
解:由频率=频数/样本容量,得到频率分布表:
分组 频数 频率
3
9
13
16
26
20
7
4
2
合计 100
(2)
解:由频率分布表中的数据,设每个小矩形的高度分布为:,
可得,,,,,,,,,
所以频率分布直方图,如图所示:
(3)
解:由频率分布直方表中的数据可得:
落在据落在的概率为
所以数据落在范围内的可能性为.
21.(1)
(2)
【解析】
【分析】
(1)设“至少有一名女生参加劳动学习”为事件A,“恰有一名女生参加劳动学习”为事件B.
根据超几何分布原理分别求得,,直接利用条件概率的计算公式即可求得;
(2)设恰有Y人女生参加劳动学习,则男生2-Y人参加劳动学习,求出Y的分布列和数学期望,由即可求出.
(1)
设“至少有一名女生参加劳动学习”为事件A,“恰有一名女生参加劳动学习”为事件B.
根据超几何分布原理得:,
有条件概率的计算公式得:
所以,在至少有一名女生参加劳动学习的条件下,恰有一名女生参加劳动学习的概率为;
(2)
根据题意女生参加劳动学习可获得:(分);
男生参加劳动学习可获得:(分).
设恰有Y人女生参加劳动学习,则男生2-Y人参加劳动学习,则
;;.
所以Y的分布列为:
Y 0 1 2
P
则有:.
又,
∴.
22.(1)说明见解析
(2),市场规模为3.632千亿元
【解析】
【分析】
(1)根据参考数据、参考公式计算相关系数,即可得出结论;
(2)根据参考数据计算,再由直线过求出,即可得出回归直线方程,代入可预测2022年中国宠物市场规模.
(1)
由题意得,,,,,
,
∴.
因为y与x的相关系数近似为0.971,趋近于1,说明y与x的线性相关程度相当强,从而可以用线性回归模型拟合y与x的关系;
(2)
由(1)得,
,
所以y关于x的线性回归方程为,
2022年对应的年份代码为7,代入,
得,
所以预测2022年中国宠物市场规模为3.632千亿元.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知随机变量X的分布列如表所示,则( )
X 1 2 3
P a 2a 3a
A. B. C. D.
2.已知随机变量的分布列如下:
若随机变量,则为( )A. B. C. D.随变化而变化
3.新能源汽车是指采用非常规的车用燃料作为动力来源(或使用常规的车用燃料、采用新型车载动力装置),综合车辆的动力控制和驱动方面的先进技术,形成的技术原理先进、具有新技术、新结构的汽车.新能源汽车包括混合动力电动汽车(HEV)、纯电动汽车(BEV,包括太阳能汽车)、燃料电池电动汽车(FCEV)、其他新能源(如超级电容器、飞轮等高效储能器)汽车等.非常规的车用燃料指除汽油、柴油之外的燃料.下表是2021年我国某地区新能源汽车的前5个月销售量与月份的统计表:
月份代码x 1 2 3 4 5
销售量y(万辆) 0.5 0.6 1 1.4 1.5
由上表可知其线性回归方程为,则的值是( ).A.0.28 B.0.32 C.0.56 D.0.64
4.已知随机变量X服从正态分布,且,则( )
A.0.1 B.0.2 C.0.3 D.0.4
5.有甲、乙、丙三个工厂生产同一型号的产品,甲厂生产的次品率为,乙厂生产的次品率为,丙厂生产的次品率为,生产出来的产品混放在一起.已知甲、乙、丙三个工厂生产的产品数分别占总数的、、,任取一件产品,则取得产品为次品的概率是( )
A. B. C. D.
6.某种元件的使用寿命超过1年的概率为0.6,使用寿命超过2年的概率为0.3,则已经使用了1年的元件,使用寿命超过2年的概率为( )
A.0.3 B.0.5 C.0.6 D.1
7.当前,新冠肺炎疫情进入常态化防控新阶段,防止疫情输入的任务依然繁重,疫情防控工作形势依然严峻、复杂.某地区安排A,B,C,D,E五名同志到三个地区开展防疫宣传活动,每个地区至少安排一人,且A,B两人安排在同一个地区,C,D两人不安排在同一个地区,则不同的分配方法总数为( )
A.30种 B.36种 C.42种 D.64种
8.在一段时间内,若甲去参观市博物馆的概率为0.8,乙去参观市博物馆的概率为0.6,且甲乙两人各自行动.则在这段时间内,甲乙两人至少有一个去参观博物馆的概率是( )
A.0.48 B.0.32 C.0.92 D.0.84
二、多选题
9.(多选题)A、B、C、D、E五个人并排站在一起,则下列说法正确的有( )
A.若A、B不相邻共有72种方法
B.若A不站在最左边,B不站最右边,有78种方法.
C.若A在B左边有60种排法
D.若A、B两人站在一起有24种方法
10.已知甲盒中仅有1个球且为红球,乙盒中有个红球和个蓝球(,,,),从乙盒中随机抽取个球放入甲盒中.
①放入个球后,甲盒中含有红球的个数记为
②放入个球后,从甲盒中取1个球是红球的概率记为.则()
A. B.
C. D.
11.若,则下列结论正确的是( )
A.若,、为整数,则
B.是正整数
C.是的小数部分
D.设,若、为整数,则
12.某人有6把钥匙,其中n把能打开门.如果随机地取一把钥匙试着开门,把不能开门的钥匙扔掉,设第二次才能打开门的概率为p,则下列结论正确的是( )
A.当时, B.当时,
C.当时, D.当时,
三、填空题
13.投掷两枚骰子,当至少一枚5点或一枚6点出现时,就说这次试验成功,则在10次试验中成功次数的均值为________.
14.在的展开式中,二项式系数之和与各项系数之和比为1:32,则的系数为___________.
15.有三个箱子,分别编号为、、.号箱装有个红球、个白球,号箱装有个红球、个白球,号箱装有个红球.某人从三个箱子中任取一箱,从中任意摸出一球,取得红球的概率为________.
四、双空题
16.在是否接种疫苗的调查中调查了7人,7人中有4人未接种疫苗,3人接种了疫苗,从这7人中随机抽取3人进行身体检查,用X表示抽取的3人中未接种疫苗的人数,则随机变量X的数学期望为______;设A为事件“抽取的3人中,既有接种疫苗的人,也有未接种疫苗的人”,则事件A发生的概率为______.
五、解答题
17.在杨辉三角中,除每行的两端数字外,每个数字都等于它左上角和右上角两个数字之和,杨辉三角开头几行如图所示.
(1)利用杨辉三角展开
(2)在杨辉三角中,哪一行会出现相邻的三个数字的比是?
18.为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时玩手机时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.
非手机控 手机控 合计
男 x m n
女 y 10 55
合计 ______ ______ ______
(1)求列表中数据的值;
(2)能否有的把握认为“手机控”与性别有关?
独立性检验临界值表:
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
参考公式及数据:,其中
19.某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次,统计数据如下表所示:
x 1 2 3 4 5 6 7
y 6 11 21 34 66 101 196
根据以上数据,绘制了如图所示的散点图.
(1)根据散点图,判断在推广期内,与(c,d均为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及题干中表格内的数据,建立y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次.参考数据:
62.14 1.54 2535 50.12 3.47
其中,.
参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计公式分别为,.
(3)推广期结束后,为更好地服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
支付方式 现金 公交卡 扫码
人次 10 60 30
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用公交卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调查结果发现:使用扫码支付的乘客中有5人次乘客享受7折优惠,有10人次乘客享受8折优惠,有15人次乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
20.为了检测某种产品的质量,抽取了1个容量为100的样本,数据的分组及各组频数如下表:
分组 频数 频率
3
9
13
16
26
20
7
4
2
合计 100
(1)完成上面的频率分布表;
(2)画出频率直方图;
(3)估计数据落在范围内的可能性.
21.某校高三2班第一小组有男生4人,女生2人,为提高中小学生对劳动教育重要性的认识,现需从中抽取2人参加学校开展的劳动技能学习,学校提供了:除草 翻地 播种 浇水四个项目.规定女生等可能的从中选择1个或者2个项目进行劳动学习,男生等可能的从中选择1个或者2个或者3个项目进行劳动学习,每参加1个劳动项目的学习获得10分,求:
(1)在至少有一名女生参加劳动学习的条件下,恰有一名女生参加劳动学习的概率;
(2)记该小组得分为X,求X的期望.
22.近年来,国民经济的增长和社会结构的变化推动宠物饲养成为很多人精神消费的主要方式,使得近几年中国宠物市场规模逐年增长,下表为2016~2020年中国宠物市场规模y(单位:千亿元),其中2016~2020年对应的年份代码x依次为1~5.
年份代码x 1 2 3 4 5
宠物市场规模y/千亿元 1.22 1.34 1.78 2.21 2.95
(1)由表中数据可知,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)求y关于x的线性回归方程,并预测2022年中国宠物市场规模.
参考数据:,,,.
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
根据分布列的性质计算可得;
【详解】
解:依题意,解得,所以;
故选:C
2.C
【解析】
【分析】
先根据概率之和为1,求得m,再求得,然后利用期望性质求解.
【详解】
因为,
所以,
所以.
又,
所以.
故选:C
3.A
【解析】
【分析】
先计算,,再根据样本中心点适合方程解得的值即可.
【详解】
由表中数据可得,,
将代入,即,解得.
故选:A.
4.D
【解析】
【分析】
利用正态曲线的对称性进行求解.
【详解】
因为随机变量X服从正态分布,
所以正态曲线关于直线对称,
又,
所以,
则.
故选:D.
5.D
【解析】
【分析】
根据三个工厂生产的产品数的占比以及次品率可求得结果.
【详解】
由题意可知,任取一件产品,则取得产品为次品的概率是.
故选:D.
6.B
【解析】
【分析】
利用条件概率的计算公式进行求解.
【详解】
设事件A为“该元件的使用寿命超过1年”,B为“该元件的使用寿命超过2年”,则,.因为,所以,
所以.
故选:B.
7.A
【解析】
【分析】
由题意可得,分两个地区各分2人,另一个地区分1人和两个地区各分1人,另一个地区分3人两种情况,对两种情况的种数求和,即可求解.
【详解】
解:①当两个地区各分2人,另一个地区分1人时,总数有种;
②当两个地区各分1人,另一个地区分3人时,总数有种.
故满足条件的分法共有种.
故选:A
8.C
【解析】
【分析】
根据题意求得甲乙都不去参观博物馆的概率,结合对立事件的概率计算公式,即可求解.
【详解】
由甲去参观市博物馆的概率为0.8,乙去参观市博物馆的概率为0.6,
可得甲乙都不去参观博物馆的概率为,
所以甲乙两人至少有一个去参观博物馆的概率是.
故选:C.
9.ABC
【解析】
【分析】
利用插空法,可判断A的正误;利用间接法,可判断B的正误;根据定序问题的求法,可判断C的正误;利用捆绑法,可判断D的正误,即可得答案.
【详解】
对于A:若A、B不相邻共有种方法,故A正确;
对于B:若A不站在最左边,B不站最右边,利用间接法有种方法,故B正确;
对于C:若A在B左边有种方法,故C正确;
对于D:若A、B两人站在一起有,故D不正确.
故选:ABC
10.AD
【解析】
【分析】
求得随机变量,的分布列,根据数学期望公式计算可得选项.
【详解】
解:因为,,所以随机变量的分布列为:
1 2
因为,,,所以随机变量的分布列为:
1 2 3
所以,,所以.
因为,,所以,所以.
故选:AD.
11.ACD
【解析】
【分析】
求出、,可判断A的正误;取可判断B的正误;利用二项式定理可判断C的正误;分为偶数和为奇数两种情况分析讨论,结合二项式定理可判断D的正误.
【详解】
对于A,,
所以,,,则,A对;
对于B,,
因为,不是正整数,B错;
对于C,因为
是正整数,
而,所以是的小数部分,C对;
对于D,因为,
当为偶数时,,
,
所以
,
所以,
即;
当为奇数时,,
,
所以
,
所以,
即,D对.
故选:ACD.
12.AC
【解析】
【分析】
根据不同的取值,分别计算对应概率求解.
【详解】
当时,,选项A正确;
当时,,选项B错误;
当时,,选项C正确;
当时,,选项D错误.
故选:AC
13.
【解析】
【分析】
先利用古典概型求得试验成功的概率,再利用二项分布均值公式求解.
【详解】
在投掷两枚骰子中,不含5或6的次数为4×4,
故试验成功的概率P=1-=,
则在10次试验中成功次数的均值E(ξ)=.
故答案为:
14.90
【解析】
【分析】
根据二项式系数的性质求得n的值,再利用二项展开式的通项公式,求得的系数.
【详解】
令,则,所以的展开式中,各项系数和为,
又二项式系数和为,所以,解得.
二项展开式的通项,令,得,
所以的系数为,
故答案为:.
15.
【解析】
【分析】
记事件为“球取自于号箱”,记事件为“取得红球”,可得出,结合全概率公式可求得结果.
【详解】
记事件为“球取自于号箱”,记事件为“取得红球”,
发生总是伴随着、、之一同时发生,即,
且、、两两互斥,
,,,,
所以,
.
故答案为:.
【点睛】
关键点点睛:本题考查利用全概率公式计算事件的概率,解题的关键在于球取自于几号袋,再结合全概率公式进行计算.
16.
【解析】
【分析】
分别求出,的概率,进一步求出所以和.
【详解】
由题意可知,随机变量X的取值范围为{0,1,2,3},
,,
,,
所以.
由已知条件可得.
故答案为:;.
17.(1)
(2)第62行会出现相邻的三个数字的比是
【解析】
【分析】
(1)根据题意得,再令,即可得答案;
(2)设在第n行出现的三个相邻的数的比是,并设这三个数分别是,,,进而根据比值关系解方程即可得答案.
(1)
解:根据杨辉三角的规律“每行两端都是1,其余每个数都等于它左上角和右上角两个数字的和”,可写出第6行的二项式系数为1,6,15,20,15,6,1,
所以.
令,,得.
(2)
解:设在第n行出现的三个相邻的数的比是,并设这三个数分别是,,,则有
所以
所以即所以
即在第62行会出现相邻的三个数字的比是.
18.(1)x=30,y=45,m=15,n=45
(2)没有95%把握认为“手机控”与性别有关
【解析】
【分析】
(1)由频率分布直方图,求出在抽取的100人中“手机控”的人数即可求解;
(2)求出2×2列联表,根据参考公式求出K2,由临界值表即可判断.
(1)
解:由频率分布直方图可知,在抽取的100人中,“手机控”有:100×(0.2+0.05)=25人,非手机控75人,
∴x=30,y=45,m=15,n=45;
(2)
解:由(1)可得2×2列联表如下:
非手机控 手机控 合计
男 30 15 45
女 45 10 55
合计 75 25 100
所以K2=≈3.030<3.841,
所以没有95%把握认为“手机控”与性别有关.
19.(1)适宜
(2),活动推出第8天使用扫码支付的人次为347
(3)199200元
【解析】
【分析】
(1)根据散点图即可判断回归方程类型;
(2)根据题意中的数据,利用最小二乘法求出,进而求出,即可得出回归方程,令求解即可;
(3)根据题意分别求出享受7折优惠、8折优惠、9折优惠的收入,进而加起来即可.
(1)
根据散点图判断,适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型.
(2)
∵,∴两边同时取常用对数,得.
设,,则.
∵,,,
∴,
,∴,∴,
把代入上式,得,
∴y关于x的回归方程为,活动推出第8天使用扫码支付的人次为347.
(3)
由题意,可知一个月中使用现金的乘客有1000人次,共收入(元);
使用公交卡的乘客有6000人次,共收入(元).
使用扫码支付的乘客有3000人次,
其中,享受7折优惠的有500人次,共收入(元),
享受8折优惠的有1000人次,共收入(元),
享受9折优惠的有1500人次,共收入(元),
故该车队一辆车一个月的收入为(元).
∴估计该车队一辆车一年的收入为(元).
20.(1)频率分布表见解析
(2)频率分布直方图见解析
(3)
【解析】
【分析】
(1)根据题目中进行列表,利用频率=频数/样本容量,求得相应的频率,即可得到分布表;
(2)根据频率/组距,得到频率分布直方图的纵坐标,进而得到频率分布直方图;
(3)根据频率分布表中的数据,即可求得范围内概率,得到答案.
(1)
解:由频率=频数/样本容量,得到频率分布表:
分组 频数 频率
3
9
13
16
26
20
7
4
2
合计 100
(2)
解:由频率分布表中的数据,设每个小矩形的高度分布为:,
可得,,,,,,,,,
所以频率分布直方图,如图所示:
(3)
解:由频率分布直方表中的数据可得:
落在据落在的概率为
所以数据落在范围内的可能性为.
21.(1)
(2)
【解析】
【分析】
(1)设“至少有一名女生参加劳动学习”为事件A,“恰有一名女生参加劳动学习”为事件B.
根据超几何分布原理分别求得,,直接利用条件概率的计算公式即可求得;
(2)设恰有Y人女生参加劳动学习,则男生2-Y人参加劳动学习,求出Y的分布列和数学期望,由即可求出.
(1)
设“至少有一名女生参加劳动学习”为事件A,“恰有一名女生参加劳动学习”为事件B.
根据超几何分布原理得:,
有条件概率的计算公式得:
所以,在至少有一名女生参加劳动学习的条件下,恰有一名女生参加劳动学习的概率为;
(2)
根据题意女生参加劳动学习可获得:(分);
男生参加劳动学习可获得:(分).
设恰有Y人女生参加劳动学习,则男生2-Y人参加劳动学习,则
;;.
所以Y的分布列为:
Y 0 1 2
P
则有:.
又,
∴.
22.(1)说明见解析
(2),市场规模为3.632千亿元
【解析】
【分析】
(1)根据参考数据、参考公式计算相关系数,即可得出结论;
(2)根据参考数据计算,再由直线过求出,即可得出回归直线方程,代入可预测2022年中国宠物市场规模.
(1)
由题意得,,,,,
,
∴.
因为y与x的相关系数近似为0.971,趋近于1,说明y与x的线性相关程度相当强,从而可以用线性回归模型拟合y与x的关系;
(2)
由(1)得,
,
所以y关于x的线性回归方程为,
2022年对应的年份代码为7,代入,
得,
所以预测2022年中国宠物市场规模为3.632千亿元.
答案第1页,共2页
答案第1页,共2页
