2021-2022学年北师大版七年级数学下册2.3平行线的性质解答题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册2.3平行线的性质解答题专题训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 238.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 17:57:57 | ||
图片预览




文档简介
2021-2022学年北师大版七年级数学下册《2-3平行线的性质》解答题专题训练(附答案)
1.如图,点H、点D在AB上,点F、点G在AC上,点E在BC上,已知HG⊥AB,DF⊥AB,∠2+∠3=180°,求证:∠1=∠A.
证明:∵HG⊥AB,DF⊥AB(已知),
∴∠AHG=∠HDF=90°(垂直的定义).
∴DF∥HG( ).
∴∠3+ =180°( ).
∵∠2+∠3=180°(已知),
∴∠2=∠4( ).
∴ (内错角相等,两直线平行).
∴∠1=∠A( ).
2.如图,已知∠A=∠3,DE⊥BC,AB⊥BC,求证:DE平分∠CDB.
证明:∵DE⊥BC,AB⊥BC(已知),
∴∠DEC=∠ABC=90°(垂直的定义).
∴DE∥AB( ).
∴∠2=∠3( ),
∠1= (两直线平行,同位角相等).
又∵∠A=∠3(已知),
∴ ( ).
∴DE平分∠CDB(角平分线的定义).
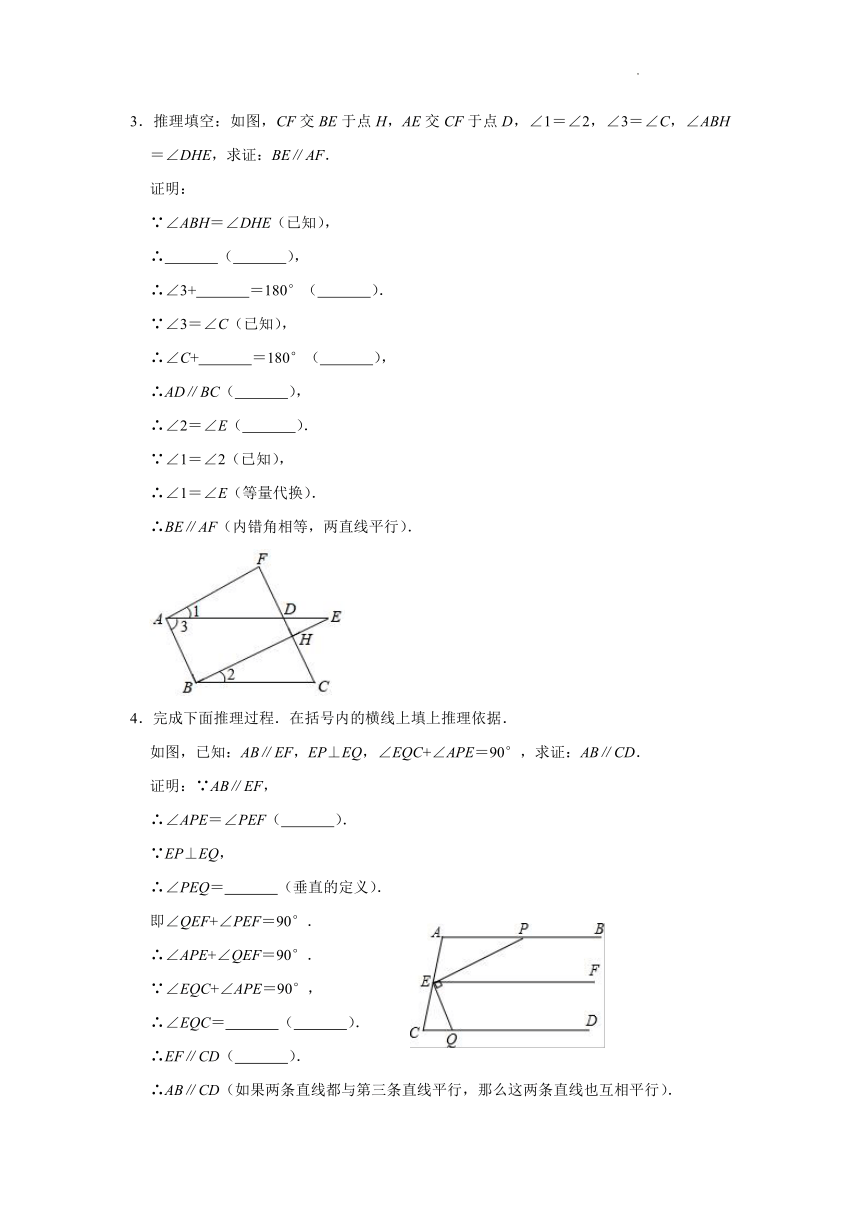
3.推理填空:如图,CF交BE于点H,AE交CF于点D,∠1=∠2,∠3=∠C,∠ABH=∠DHE,求证:BE∥AF.
证明:
∵∠ABH=∠DHE(已知),
∴ ( ),
∴∠3+ =180°( ).
∵∠3=∠C(已知),
∴∠C+ =180°( ),
∴AD∥BC( ),
∴∠2=∠E( ).
∵∠1=∠2(已知),
∴∠1=∠E(等量代换).
∴BE∥AF(内错角相等,两直线平行).
4.完成下面推理过程.在括号内的横线上填上推理依据.
如图,已知:AB∥EF,EP⊥EQ,∠EQC+∠APE=90°,求证:AB∥CD.
证明:∵AB∥EF,
∴∠APE=∠PEF( ).
∵EP⊥EQ,
∴∠PEQ= (垂直的定义).
即∠QEF+∠PEF=90°.
∴∠APE+∠QEF=90°.
∵∠EQC+∠APE=90°,
∴∠EQC= ( ).
∴EF∥CD( ).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
5.完成下面的证明:
看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.
证明:∵AD⊥BC于D,EG⊥BC于G( ),
∴∠ADC=90°,∠EGC=90°( ).
∴∠ADC=∠EGC( ).
∴AD∥EG( ).
∴∠1=∠ ( ),
∠2=∠ ( ).
又∵∠E=∠3(已知),
∴∠1=∠2( ),
∴AD平分∠BAC( ).
6.填空,完成下列证明过程,并在括号中注明理由.如图,已知∠BEF+∠EFD=180°,∠AEG=∠HFD,求证:∠G=∠H.
证明:
∵∠BEF+∠EFD=180°, .
∴AB∥ ( ).
∴ =∠EFD( ).
又∵∠AEG=∠HFD,
∴∠AEF﹣∠AEG=∠EFD﹣∠HFD,
即 = .
∴ ∥FH( ).
∴∠G=∠H.( ).
7.如图,已知BD⊥AF,CE⊥AF,∠C=∠D,求证:∠A=∠F.
请将下列证明过程补充完整:
∵BD⊥AF,CE⊥AF( ),
∴∠1 =90°( ).
∴BD∥CE( ).
∴∠3+∠C=180°( ).
∵∠C=∠D ,
∴∠3+ =180°( ).
∴AC∥DF( ).
∴∠A=∠F( ).
8.如图,在四边形ABCD中.点E为AB延长线上一点,点F为CD延长线上一点,连接EF,交BC于点G,交AD于点H,若∠1=∠2,∠A=∠C,求证:∠E=∠F.
证明:∵∠1=∠3( ),
∠1=∠2(已知).
∴∠2=∠3(等量代换).
∴AD∥BC( ).
∴∠A+∠4=180°( ).
∵∠A=∠C(已知),
∴∠C+∠4=180°(等量代换).
∴ ∥ (同旁内角互补,两直线平行).
∴∠E=∠F( ).
9.如图,点D、E分别为AB、AC上的点,点F、G为BC上的点,连接DE,连接DG、EF交于点H.已知∠1+∠2=180°,∠B=∠3,若∠C=66°,求∠DEC的度数.请你将下面解答过程填写完整.
解:∵∠1+∠2=180°,
∴AB∥ .
∴∠ADE=∠3( ).
∵∠B=∠3,
∴ =∠B.
∴DE∥BC( ).
∴∠C+∠DEC=180°.
∵∠C=66°,
∴∠DEC=114°.
10.如图所示,已知BD⊥CD于D,EF⊥CD于F,∠A=80°,∠ABC=100°.求证:∠1=∠2.证明:∵BD⊥CD,EF⊥CD(已知),
∴∠BDC=∠EFC=90°(垂直的定义).
∴ (同位角相等,两直线平行).
∴∠2=∠3( ).
∵∠A=80°,∠ABC=100°(已知),
∴∠A+∠ABC=180°.
∴AD∥BC( ).
∴ (两直线平行,内错角相等).
∴∠1=∠2( ).
11.推理填空:
已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE.
证明:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠
∴∠3=∠ ( )
∴AD∥BE( )
12.如图,已知∠1=∠2,∠C=∠D,求证:∠A=∠F.
13.如图,AE∥DF,∠B+∠1=90°,BE⊥FD于G.求证:AB∥CD.
14.如图,AD∥BC,∠B=∠C,∠1=60°.
(1)求∠C的度数;
(2)如果AE是∠BAD的平分线,那么AE与DC平行吗?请说明理由.
15.如图,DF平分∠ADC,BE平分∠ABC,∠AEB=∠ABC.
(1)求证:AD与BC平行;
(2)若∠ABC=∠ADC,DF与BE存在什么样的位置关系?请说明理由.
16.如图,AE⊥BC,DF⊥BC,且∠1=∠2.
(1)判断AB与CD是否平行,并请说明理由;
(2)若BC平分∠ABD,且∠BDC=∠3+90°,求∠C的度数.
17.如图,AB∥CD,CH平分∠ACD交AB于点H,AE平分∠FAB.
(1)求证:AE∥CH;
(2)若∠AHC=62°,求∠ACH的度数.
18.如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)AD与EC平行吗?试说明理由.
(2)若DA平分∠BDC,CE⊥AE于点E,∠1=80°,试求∠FAB的度数.
19.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AD∥BC.
20.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.
21.如图1,在三角形ABC中,点E、点F分别为线段AB、AC上任意两点,EG交BC于G,交AC的延长线于H,∠1+∠AFE=180°.
(1)求证:BC∥EF;
(2)如图2,若∠2=∠3,∠BEG=∠EDF,求证:DF平分∠AFE.
参考答案
1.证明:∵HG⊥AB,DF⊥AB(已知),
∴∠AHG=∠HDF=90°(垂直的定义).
∴DF∥HG(同位角相等,两直线平行),
∴∠3+∠4=180°(两直线平行,同旁内角互补),
∵∠2+∠3=180°(已知),
∴∠2=∠4(等量代换),
∴DE∥AC(内错角相等,两直线平行).
∴∠1=∠A(两直线平行,同位角相等).
故答案为:同位角相等,两直线平行;∠4,两直线平行,同旁内角互补;等量代换;DE∥AC;两直线平行,同位角相等.
2.证明:∵DE⊥BC,AB⊥BC(已知),
∴∠DEC=∠ABC=90°(垂直的定义).
∴DE∥AB(同位角相等,两直线平行).
∴∠2=∠3(两直线平行,内错角相等),
∠1=∠A(两直线平行,同位角相等).
又∵∠A=∠3(已知),
∴∠1=∠2(等量代换).
∴DE平分∠CDB(角平分线的定义).
故答案为:同位角相等,两直线平行;两直线平行,内错角相等;∠A;∠1=∠2,等量代换.
3.证明:∵∠ABH=∠DHE(已知),
∴AB∥CF(同位角相等,两直线平行 ),
∴∠3+∠ADC=180°( 两直线平行,同旁内角互补),
∵∠3=∠C(已知),
∴∠C+∠ADC=180°(等角的补角相等 ),
∴AD∥BC(同旁内角互补,两直线平行 ),
∴∠2=∠E(两直线平行,内错角相等 ).
∵∠1=∠2(已知),
∴∠1=∠E(等量代换),
∴BE∥AF(内错角相等,两直线平行).
故答案为:AB∥CF,同位角相等,两直线平行;∠ADC,两直线平行,同旁内角互补;∠ADC,等角的补角相等;同旁内角互补,两直线平行;两直线平行,内错角相等.
4.解:∵AB∥EF,
∴∠APE=∠PEF(两直线平行,内错角相等).
∵EP⊥EQ,
∴∠PEQ=90°(垂直的定义).
即∠QEF+∠PEF=90°.
∴∠APE+∠QEF=90°.
∵∠EQC+∠APE=90°,
∴∠EQC=∠QEF(同角的余角相等).
∴EF∥CD(内错角相等,两直线平行).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
故答案为:两直线平行,内错角相等;90°;∠QEF;同角的余角相等;内错角相等,两直线平行.
5.证明:∵AD⊥BC于D,EG⊥BC于G(已知),
∴∠ADC=90°,∠EGC=90°(垂直定义).
∴∠ADC=∠EGC(等量代换).
∴AD∥EG(同位角相等,两直线平行).
∴∠1=∠3(两直线平行,内错角相等),
∠2=∠E(两直线平行,同位角相等).
又∵∠E=∠3(已知),
∴∠1=∠2(等量代换),
∴AD平分∠BAC(角平分线的定义).
故答案为:已知;垂直定义;等量代换;同位角相等,两直线平行;3,两直线平行,内错角相等;E,两直线平行,同位角相等;等量代换;角平分线的定义.
6.证明:∵∠BEF+∠EFD=180°(已知),
∴AB∥CD(同旁内角互补,两直线平行),
∴∠AEF=∠EFD(两直线平行,内错角相等),
又∵∠AEG=∠HFD,
∴∠AEF﹣∠AEG=∠EFD﹣∠HFD,
即∠GEF=∠HFE,
∴EG∥FH(内错角相等,两直线平行),
∴∠G=∠H(两直线平行,内错角相等),
故答案为:已知,CD,同旁内角互补,两直线平行,∠AEF,两直线平行,内错角相等,∠GEF,∠HFE,EG,内错角相等,两直线平行,两直线平行,内错角相等.
7.∵BD⊥AF,CE⊥AF(已知),
∴∠1=∠2=90°(垂直定义).
∴BD∥CE( 同位角相等,两直线平行).
∴∠3+∠C=180°(两直线平行,同旁内角互补 ).
∵∠C=∠D(已知),
∴∠3+∠D=180°( 等量代换).
∴AC∥DF(同旁内角互补,两直线平行).
∴∠A=∠F(两直线平行,内错角相等).
故答案为:已知;=∠2,垂直定义;同位角相等,两直线平行;两直线平行,同旁内角互补;已知;,∠D,等量代换;同旁内角互补,两直线平行;两直线平行,内错角相等.
8.证明:∵∠1=∠3(对顶角相等),
∠1=∠2(已知).
∴∠2=∠3(等量代换).
∴AD∥BC(同位角相等,两直线平行).
∴∠A+∠4=180°(两直线平行,同旁内角互补).
∵∠A=∠C(已知),
∴∠C+∠4=180°(等量代换).
∴CF∥EA(同旁内角互补,两直线平行).
∴∠E=∠F(两直线平行,内错角相等).
故答案为:对顶角相等;同位角相等,两直线平行;两直线平行,同旁内角互补;CF,EA;两直线平行,内错角相等.
9.解:∵∠1+∠2=180°,
∴AB∥EF,
∴∠ADE=∠3(两直线平行,内错角相等),
∵∠B=∠3,
∴∠ADE=∠B.
∴DE∥BC(同位角相等,两直线平行),
∴∠C+∠DEC=180°.
∵∠C=66°,
∴∠DEC=114°.
故答案为:EF;两直线平行,内错角相等;∠ADE;同位角相等,两直线平行.
10.证明:∵BD⊥CD,EF⊥DC,
∴∠BDC=∠EFC=90°,
∴BD∥EF,
∴∠2=∠3(两直线平行,同位角相等),
∵∠A=80°,∠ABC=100°,
∴∠A+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠1=∠3,
∴∠1=∠2(等量代换).
故答案为:BD∥EF;两直线平行,同位角相等;同旁内角互补,两直线平行;∠1=∠3;等量代换.
11.(每空1分)推理填空:
已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE.
证明:∵AB∥CD(已知)
∴∠4=∠BAF(两直线平行,同位角相等)
∵∠3=∠4(已知)
∴∠3=∠BAF(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠CAD
∴∠3=∠CAD(等量代换)
∴AD∥BE(内错角相等,两直线平行).
故答案为:
∠BAF(两直线平行,同位角相等);
∠4(已知);
∠BAF(等量代换);
等量代换;
内错角相等,两直线平行;
12.证明:∵∠1=∠2,
∴BD∥CE,
∴∠C+∠CBD=180°,
∵∠C=∠D,
∴∠D+∠CBD=180°,
∴AC∥DF,
∴∠A=∠F.
13.证明:∵BE⊥FD,
∴∠DGE=90°,
∴∠DEG+∠D=90°,
∵AE∥DF,
∴∠1=∠D,
∵∠B+∠1=90°,
∴∠B=∠DEG,
∴AB∥CD.
14.解:(1)∵AD∥BC,∠1=60°.
∴∠B=∠1=60°,
∴∠C=∠B=60°.
(2)AE∥DC,理由如下:
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE==,
∵AD∥BC,
∴∠BEA=∠DAE=60°,
又∵∠C=60°,
∴∠BEA=∠C,
AE∥DC.
15.证明:(1)因为BE平分∠ABC,
所以∠ABE=∠CBE=,
又因为∠AEB=∠ABC,
所以∠CBE=∠AEB,
所以AD∥BC(内错角相等,两直线平行);
(2)BE∥DF.
理由如下:
因为DF平分∠ADC,
所以,
又因为∠AEB=∠ABC,∠ABC=∠ADC,
所以∠AEB=∠ADF,
所以BE∥DF(同位角相等,两直线平行).
16.解:(1)AB∥CD,理由如下:
∵AE⊥BC,DF⊥BC,
∴DF∥AE,
∴∠A=∠2,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)∵AB∥CD,
∴∠ABD+∠BDC=180°,
∵BC平分∠ABD,
∴∠ABD=2∠3,
∵∠BDC=∠3+90°,
∴2∠3+∠3+90°=180°,
∴∠3=30°,
∵AB∥CD,
∴∠C=∠3=30°.
所以∠C的度数为30°.
17.(1)证明:∵AB∥CD,
∴∠FAB=∠FCD,
∵AE平分∠FAB,CH平分∠ACD,
∴∠FAE=∠FAB,∠FCH=∠FCD,
∴∠FAE=∠FCH,
∴AE∥CH;
(2)∵AB∥CD,
∴∠AHC=∠HCD,
∵∠AHC=62°,
∴∠HCD=62°,
∵CH平分∠ACD,
∴∠ACH=∠HCD=62°.
18.(1)AD与EC平行,
证明:∵∠1=∠BDC,
∴AB∥CD(同位角相等,两直线平行),
∴∠2=∠ADC(两直线平行,内错角相等),
∵∠2+∠3=180°,
∴∠ADC+∠3=180°(等量代换),
∴AD∥CE(同旁内角互补,两直线平行);
(2)解:∵∠1=∠BDC,∠1=80°,
∴∠BDC=80°,
∵DA平分∠BDC,
∴∠ADC=∠BDC=40°(角平分线定义),
∴∠2=∠ADC=40°(已证),
又∵CE⊥AE,
∴∠AEC=90°(垂直定义),
∵AD∥CE(已证),
∴∠FAD=∠AEC=90°(两直线平行,同位角相等),
∴∠FAB=∠FAD﹣∠2=90°﹣40°=50°.
19.解:∵AB∥CD,
∴∠BAE=∠CFE,
∵AE平分∠BAD,
∴∠BAE=∠DAF,
∵∠CFE=∠E,
∴∠DAF=∠E,
∴AD∥BC.
20.(1)证明:∵AE⊥BC,FG⊥BC,
∴AE∥GF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠CBD+∠3=180°,
∵∠D=∠3+60°,∠CBD=70°,
∴∠3=25°,
∵AB∥CD,
∴∠C=∠3=25°.
21.证明:(1)∵∠1+∠AFE=180°,∠1+∠CFE=180°,
∴∠AFE=∠CFE,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
1.如图,点H、点D在AB上,点F、点G在AC上,点E在BC上,已知HG⊥AB,DF⊥AB,∠2+∠3=180°,求证:∠1=∠A.
证明:∵HG⊥AB,DF⊥AB(已知),
∴∠AHG=∠HDF=90°(垂直的定义).
∴DF∥HG( ).
∴∠3+ =180°( ).
∵∠2+∠3=180°(已知),
∴∠2=∠4( ).
∴ (内错角相等,两直线平行).
∴∠1=∠A( ).
2.如图,已知∠A=∠3,DE⊥BC,AB⊥BC,求证:DE平分∠CDB.
证明:∵DE⊥BC,AB⊥BC(已知),
∴∠DEC=∠ABC=90°(垂直的定义).
∴DE∥AB( ).
∴∠2=∠3( ),
∠1= (两直线平行,同位角相等).
又∵∠A=∠3(已知),
∴ ( ).
∴DE平分∠CDB(角平分线的定义).
3.推理填空:如图,CF交BE于点H,AE交CF于点D,∠1=∠2,∠3=∠C,∠ABH=∠DHE,求证:BE∥AF.
证明:
∵∠ABH=∠DHE(已知),
∴ ( ),
∴∠3+ =180°( ).
∵∠3=∠C(已知),
∴∠C+ =180°( ),
∴AD∥BC( ),
∴∠2=∠E( ).
∵∠1=∠2(已知),
∴∠1=∠E(等量代换).
∴BE∥AF(内错角相等,两直线平行).
4.完成下面推理过程.在括号内的横线上填上推理依据.
如图,已知:AB∥EF,EP⊥EQ,∠EQC+∠APE=90°,求证:AB∥CD.
证明:∵AB∥EF,
∴∠APE=∠PEF( ).
∵EP⊥EQ,
∴∠PEQ= (垂直的定义).
即∠QEF+∠PEF=90°.
∴∠APE+∠QEF=90°.
∵∠EQC+∠APE=90°,
∴∠EQC= ( ).
∴EF∥CD( ).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
5.完成下面的证明:
看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.
证明:∵AD⊥BC于D,EG⊥BC于G( ),
∴∠ADC=90°,∠EGC=90°( ).
∴∠ADC=∠EGC( ).
∴AD∥EG( ).
∴∠1=∠ ( ),
∠2=∠ ( ).
又∵∠E=∠3(已知),
∴∠1=∠2( ),
∴AD平分∠BAC( ).
6.填空,完成下列证明过程,并在括号中注明理由.如图,已知∠BEF+∠EFD=180°,∠AEG=∠HFD,求证:∠G=∠H.
证明:
∵∠BEF+∠EFD=180°, .
∴AB∥ ( ).
∴ =∠EFD( ).
又∵∠AEG=∠HFD,
∴∠AEF﹣∠AEG=∠EFD﹣∠HFD,
即 = .
∴ ∥FH( ).
∴∠G=∠H.( ).
7.如图,已知BD⊥AF,CE⊥AF,∠C=∠D,求证:∠A=∠F.
请将下列证明过程补充完整:
∵BD⊥AF,CE⊥AF( ),
∴∠1 =90°( ).
∴BD∥CE( ).
∴∠3+∠C=180°( ).
∵∠C=∠D ,
∴∠3+ =180°( ).
∴AC∥DF( ).
∴∠A=∠F( ).
8.如图,在四边形ABCD中.点E为AB延长线上一点,点F为CD延长线上一点,连接EF,交BC于点G,交AD于点H,若∠1=∠2,∠A=∠C,求证:∠E=∠F.
证明:∵∠1=∠3( ),
∠1=∠2(已知).
∴∠2=∠3(等量代换).
∴AD∥BC( ).
∴∠A+∠4=180°( ).
∵∠A=∠C(已知),
∴∠C+∠4=180°(等量代换).
∴ ∥ (同旁内角互补,两直线平行).
∴∠E=∠F( ).
9.如图,点D、E分别为AB、AC上的点,点F、G为BC上的点,连接DE,连接DG、EF交于点H.已知∠1+∠2=180°,∠B=∠3,若∠C=66°,求∠DEC的度数.请你将下面解答过程填写完整.
解:∵∠1+∠2=180°,
∴AB∥ .
∴∠ADE=∠3( ).
∵∠B=∠3,
∴ =∠B.
∴DE∥BC( ).
∴∠C+∠DEC=180°.
∵∠C=66°,
∴∠DEC=114°.
10.如图所示,已知BD⊥CD于D,EF⊥CD于F,∠A=80°,∠ABC=100°.求证:∠1=∠2.证明:∵BD⊥CD,EF⊥CD(已知),
∴∠BDC=∠EFC=90°(垂直的定义).
∴ (同位角相等,两直线平行).
∴∠2=∠3( ).
∵∠A=80°,∠ABC=100°(已知),
∴∠A+∠ABC=180°.
∴AD∥BC( ).
∴ (两直线平行,内错角相等).
∴∠1=∠2( ).
11.推理填空:
已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE.
证明:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠
∴∠3=∠ ( )
∴AD∥BE( )
12.如图,已知∠1=∠2,∠C=∠D,求证:∠A=∠F.
13.如图,AE∥DF,∠B+∠1=90°,BE⊥FD于G.求证:AB∥CD.
14.如图,AD∥BC,∠B=∠C,∠1=60°.
(1)求∠C的度数;
(2)如果AE是∠BAD的平分线,那么AE与DC平行吗?请说明理由.
15.如图,DF平分∠ADC,BE平分∠ABC,∠AEB=∠ABC.
(1)求证:AD与BC平行;
(2)若∠ABC=∠ADC,DF与BE存在什么样的位置关系?请说明理由.
16.如图,AE⊥BC,DF⊥BC,且∠1=∠2.
(1)判断AB与CD是否平行,并请说明理由;
(2)若BC平分∠ABD,且∠BDC=∠3+90°,求∠C的度数.
17.如图,AB∥CD,CH平分∠ACD交AB于点H,AE平分∠FAB.
(1)求证:AE∥CH;
(2)若∠AHC=62°,求∠ACH的度数.
18.如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)AD与EC平行吗?试说明理由.
(2)若DA平分∠BDC,CE⊥AE于点E,∠1=80°,试求∠FAB的度数.
19.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AD∥BC.
20.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.
21.如图1,在三角形ABC中,点E、点F分别为线段AB、AC上任意两点,EG交BC于G,交AC的延长线于H,∠1+∠AFE=180°.
(1)求证:BC∥EF;
(2)如图2,若∠2=∠3,∠BEG=∠EDF,求证:DF平分∠AFE.
参考答案
1.证明:∵HG⊥AB,DF⊥AB(已知),
∴∠AHG=∠HDF=90°(垂直的定义).
∴DF∥HG(同位角相等,两直线平行),
∴∠3+∠4=180°(两直线平行,同旁内角互补),
∵∠2+∠3=180°(已知),
∴∠2=∠4(等量代换),
∴DE∥AC(内错角相等,两直线平行).
∴∠1=∠A(两直线平行,同位角相等).
故答案为:同位角相等,两直线平行;∠4,两直线平行,同旁内角互补;等量代换;DE∥AC;两直线平行,同位角相等.
2.证明:∵DE⊥BC,AB⊥BC(已知),
∴∠DEC=∠ABC=90°(垂直的定义).
∴DE∥AB(同位角相等,两直线平行).
∴∠2=∠3(两直线平行,内错角相等),
∠1=∠A(两直线平行,同位角相等).
又∵∠A=∠3(已知),
∴∠1=∠2(等量代换).
∴DE平分∠CDB(角平分线的定义).
故答案为:同位角相等,两直线平行;两直线平行,内错角相等;∠A;∠1=∠2,等量代换.
3.证明:∵∠ABH=∠DHE(已知),
∴AB∥CF(同位角相等,两直线平行 ),
∴∠3+∠ADC=180°( 两直线平行,同旁内角互补),
∵∠3=∠C(已知),
∴∠C+∠ADC=180°(等角的补角相等 ),
∴AD∥BC(同旁内角互补,两直线平行 ),
∴∠2=∠E(两直线平行,内错角相等 ).
∵∠1=∠2(已知),
∴∠1=∠E(等量代换),
∴BE∥AF(内错角相等,两直线平行).
故答案为:AB∥CF,同位角相等,两直线平行;∠ADC,两直线平行,同旁内角互补;∠ADC,等角的补角相等;同旁内角互补,两直线平行;两直线平行,内错角相等.
4.解:∵AB∥EF,
∴∠APE=∠PEF(两直线平行,内错角相等).
∵EP⊥EQ,
∴∠PEQ=90°(垂直的定义).
即∠QEF+∠PEF=90°.
∴∠APE+∠QEF=90°.
∵∠EQC+∠APE=90°,
∴∠EQC=∠QEF(同角的余角相等).
∴EF∥CD(内错角相等,两直线平行).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
故答案为:两直线平行,内错角相等;90°;∠QEF;同角的余角相等;内错角相等,两直线平行.
5.证明:∵AD⊥BC于D,EG⊥BC于G(已知),
∴∠ADC=90°,∠EGC=90°(垂直定义).
∴∠ADC=∠EGC(等量代换).
∴AD∥EG(同位角相等,两直线平行).
∴∠1=∠3(两直线平行,内错角相等),
∠2=∠E(两直线平行,同位角相等).
又∵∠E=∠3(已知),
∴∠1=∠2(等量代换),
∴AD平分∠BAC(角平分线的定义).
故答案为:已知;垂直定义;等量代换;同位角相等,两直线平行;3,两直线平行,内错角相等;E,两直线平行,同位角相等;等量代换;角平分线的定义.
6.证明:∵∠BEF+∠EFD=180°(已知),
∴AB∥CD(同旁内角互补,两直线平行),
∴∠AEF=∠EFD(两直线平行,内错角相等),
又∵∠AEG=∠HFD,
∴∠AEF﹣∠AEG=∠EFD﹣∠HFD,
即∠GEF=∠HFE,
∴EG∥FH(内错角相等,两直线平行),
∴∠G=∠H(两直线平行,内错角相等),
故答案为:已知,CD,同旁内角互补,两直线平行,∠AEF,两直线平行,内错角相等,∠GEF,∠HFE,EG,内错角相等,两直线平行,两直线平行,内错角相等.
7.∵BD⊥AF,CE⊥AF(已知),
∴∠1=∠2=90°(垂直定义).
∴BD∥CE( 同位角相等,两直线平行).
∴∠3+∠C=180°(两直线平行,同旁内角互补 ).
∵∠C=∠D(已知),
∴∠3+∠D=180°( 等量代换).
∴AC∥DF(同旁内角互补,两直线平行).
∴∠A=∠F(两直线平行,内错角相等).
故答案为:已知;=∠2,垂直定义;同位角相等,两直线平行;两直线平行,同旁内角互补;已知;,∠D,等量代换;同旁内角互补,两直线平行;两直线平行,内错角相等.
8.证明:∵∠1=∠3(对顶角相等),
∠1=∠2(已知).
∴∠2=∠3(等量代换).
∴AD∥BC(同位角相等,两直线平行).
∴∠A+∠4=180°(两直线平行,同旁内角互补).
∵∠A=∠C(已知),
∴∠C+∠4=180°(等量代换).
∴CF∥EA(同旁内角互补,两直线平行).
∴∠E=∠F(两直线平行,内错角相等).
故答案为:对顶角相等;同位角相等,两直线平行;两直线平行,同旁内角互补;CF,EA;两直线平行,内错角相等.
9.解:∵∠1+∠2=180°,
∴AB∥EF,
∴∠ADE=∠3(两直线平行,内错角相等),
∵∠B=∠3,
∴∠ADE=∠B.
∴DE∥BC(同位角相等,两直线平行),
∴∠C+∠DEC=180°.
∵∠C=66°,
∴∠DEC=114°.
故答案为:EF;两直线平行,内错角相等;∠ADE;同位角相等,两直线平行.
10.证明:∵BD⊥CD,EF⊥DC,
∴∠BDC=∠EFC=90°,
∴BD∥EF,
∴∠2=∠3(两直线平行,同位角相等),
∵∠A=80°,∠ABC=100°,
∴∠A+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠1=∠3,
∴∠1=∠2(等量代换).
故答案为:BD∥EF;两直线平行,同位角相等;同旁内角互补,两直线平行;∠1=∠3;等量代换.
11.(每空1分)推理填空:
已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE.
证明:∵AB∥CD(已知)
∴∠4=∠BAF(两直线平行,同位角相等)
∵∠3=∠4(已知)
∴∠3=∠BAF(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠CAD
∴∠3=∠CAD(等量代换)
∴AD∥BE(内错角相等,两直线平行).
故答案为:
∠BAF(两直线平行,同位角相等);
∠4(已知);
∠BAF(等量代换);
等量代换;
内错角相等,两直线平行;
12.证明:∵∠1=∠2,
∴BD∥CE,
∴∠C+∠CBD=180°,
∵∠C=∠D,
∴∠D+∠CBD=180°,
∴AC∥DF,
∴∠A=∠F.
13.证明:∵BE⊥FD,
∴∠DGE=90°,
∴∠DEG+∠D=90°,
∵AE∥DF,
∴∠1=∠D,
∵∠B+∠1=90°,
∴∠B=∠DEG,
∴AB∥CD.
14.解:(1)∵AD∥BC,∠1=60°.
∴∠B=∠1=60°,
∴∠C=∠B=60°.
(2)AE∥DC,理由如下:
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE==,
∵AD∥BC,
∴∠BEA=∠DAE=60°,
又∵∠C=60°,
∴∠BEA=∠C,
AE∥DC.
15.证明:(1)因为BE平分∠ABC,
所以∠ABE=∠CBE=,
又因为∠AEB=∠ABC,
所以∠CBE=∠AEB,
所以AD∥BC(内错角相等,两直线平行);
(2)BE∥DF.
理由如下:
因为DF平分∠ADC,
所以,
又因为∠AEB=∠ABC,∠ABC=∠ADC,
所以∠AEB=∠ADF,
所以BE∥DF(同位角相等,两直线平行).
16.解:(1)AB∥CD,理由如下:
∵AE⊥BC,DF⊥BC,
∴DF∥AE,
∴∠A=∠2,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)∵AB∥CD,
∴∠ABD+∠BDC=180°,
∵BC平分∠ABD,
∴∠ABD=2∠3,
∵∠BDC=∠3+90°,
∴2∠3+∠3+90°=180°,
∴∠3=30°,
∵AB∥CD,
∴∠C=∠3=30°.
所以∠C的度数为30°.
17.(1)证明:∵AB∥CD,
∴∠FAB=∠FCD,
∵AE平分∠FAB,CH平分∠ACD,
∴∠FAE=∠FAB,∠FCH=∠FCD,
∴∠FAE=∠FCH,
∴AE∥CH;
(2)∵AB∥CD,
∴∠AHC=∠HCD,
∵∠AHC=62°,
∴∠HCD=62°,
∵CH平分∠ACD,
∴∠ACH=∠HCD=62°.
18.(1)AD与EC平行,
证明:∵∠1=∠BDC,
∴AB∥CD(同位角相等,两直线平行),
∴∠2=∠ADC(两直线平行,内错角相等),
∵∠2+∠3=180°,
∴∠ADC+∠3=180°(等量代换),
∴AD∥CE(同旁内角互补,两直线平行);
(2)解:∵∠1=∠BDC,∠1=80°,
∴∠BDC=80°,
∵DA平分∠BDC,
∴∠ADC=∠BDC=40°(角平分线定义),
∴∠2=∠ADC=40°(已证),
又∵CE⊥AE,
∴∠AEC=90°(垂直定义),
∵AD∥CE(已证),
∴∠FAD=∠AEC=90°(两直线平行,同位角相等),
∴∠FAB=∠FAD﹣∠2=90°﹣40°=50°.
19.解:∵AB∥CD,
∴∠BAE=∠CFE,
∵AE平分∠BAD,
∴∠BAE=∠DAF,
∵∠CFE=∠E,
∴∠DAF=∠E,
∴AD∥BC.
20.(1)证明:∵AE⊥BC,FG⊥BC,
∴AE∥GF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠CBD+∠3=180°,
∵∠D=∠3+60°,∠CBD=70°,
∴∠3=25°,
∵AB∥CD,
∴∠C=∠3=25°.
21.证明:(1)∵∠1+∠AFE=180°,∠1+∠CFE=180°,
∴∠AFE=∠CFE,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
