苏科版七年级数学下册 11.6 一元一次不等式组 课件(共21张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 11.6 一元一次不等式组 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 319.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
11.6 一元一次不等式组
11.6 一元一次不等式组(1)
七年级(下册)
初中数学
用不等式表示下列数量关系:
2.一个两位数的十位数字是x,个位数字比十位数字小2,这个两位数不大于55,又不小于23。
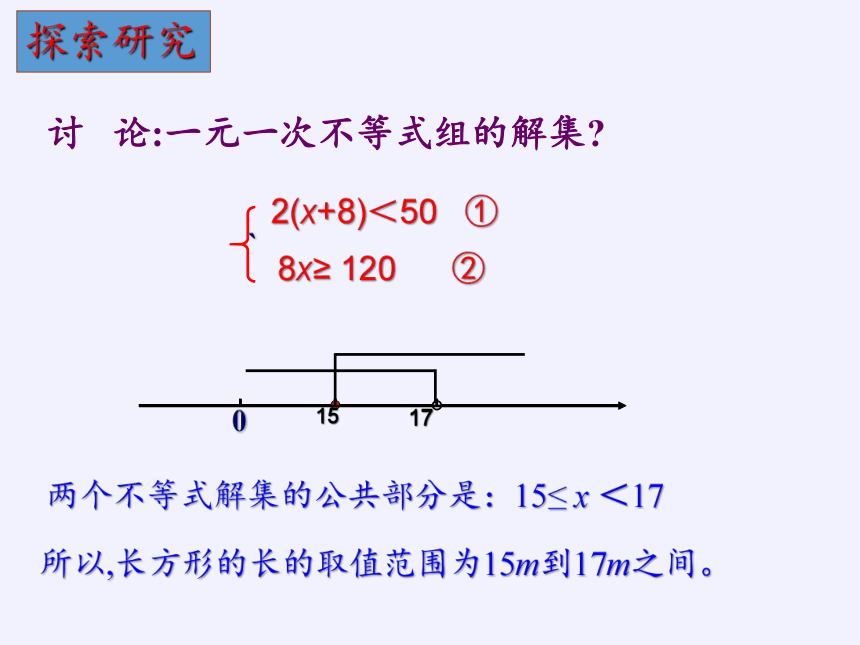
1.一块长方形的土地的宽是8m,周长小于50m,面积至少是120m2,求长方形长的取值范围.
11.6-1 一元一次不等式组
特点:未知数要满足的不等关系不止一个,列出的满足未知数数量关系的不等式也不止一个.
像这样,由几个含有同一个未知数的一元一次不等式组成的不等式组叫做一元一次不等式组.
判断下列不等式组中哪些是一元一次不等式组:
√
√
0
15
17
两个不等式解集的公共部分是:15≤ x <17
2(x+8)<50 ①
8x≥ 120 ②
`
所以,长方形的长的取值范围为15m到17m之间。
探索研究
0
15
17
讨 论:一元一次不等式组的解集
不等式组中所有不等式的解集的公共部分,叫做这个不等式组的解集.
求不等式组的解集的过程,叫做解不等式组.
知识归纳
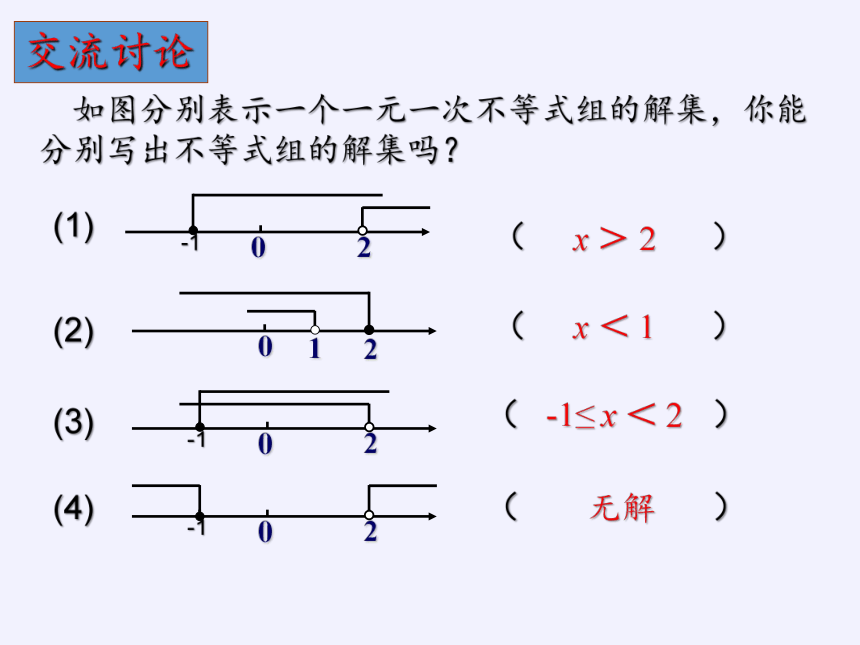
如图分别表示一个一元一次不等式组的解集,你能分别写出不等式组的解集吗?
(2)
0
2
1
(1)
0
2
-1
(3)
0
2
-1
( )
( )
( )
( )
(4)
0
2
-1
x > 2
x < 1
-1≤ x < 2
无解
交流讨论
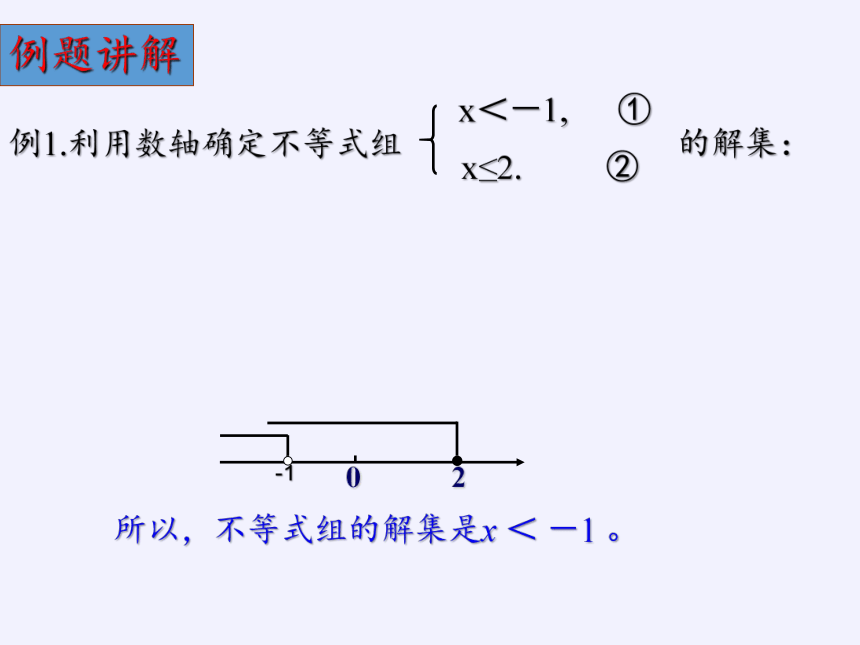
例1.利用数轴确定不等式组 的解集:
x<-1, ①
x≤2. ②
所以,不等式组的解集是x < -1 。
0
2
-1
例题讲解
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
②
④
①
③
-2 -1 0 1 2
议一议: (用数轴来解释)
在① ② ③ ④
各个一元一次不等式组中,两个不等式里x的值,
有公共部分的是: ;
没有公共部分的是: .
由于不等式组中的两个不等式的解集没有公共部分,此时我们称这个不等式组无解.
-5
-2
0
-3
-1
-4
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
借助数轴求下列不等式组的解集:
同大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
借助数轴求下列不等式组的解集:
同小取小
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
借助数轴求下列不等式组的解集:
大小小大中间找
借助数轴求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小解不了
练习:借助数轴求下列不等式组的解集:
练习:借助数轴求下列不等式组的解集:
能力提升:
1、一元一次不等式组 的解集是什么?
能力提升:
2、若不等式组
有解,求a的取值范围.
能力提升:
3、若不等式组
的解集为
.
的取值范围是
则
小结思考
1、什么是一元一次不等式组?
2、什么是不等式组的解集?
3、怎样解不等式组?
4、如何借助数轴确定不等式组的解集?
谢 谢
11.6 一元一次不等式组
11.6 一元一次不等式组(1)
七年级(下册)
初中数学
用不等式表示下列数量关系:
2.一个两位数的十位数字是x,个位数字比十位数字小2,这个两位数不大于55,又不小于23。
1.一块长方形的土地的宽是8m,周长小于50m,面积至少是120m2,求长方形长的取值范围.
11.6-1 一元一次不等式组
特点:未知数要满足的不等关系不止一个,列出的满足未知数数量关系的不等式也不止一个.
像这样,由几个含有同一个未知数的一元一次不等式组成的不等式组叫做一元一次不等式组.
判断下列不等式组中哪些是一元一次不等式组:
√
√
0
15
17
两个不等式解集的公共部分是:15≤ x <17
2(x+8)<50 ①
8x≥ 120 ②
`
所以,长方形的长的取值范围为15m到17m之间。
探索研究
0
15
17
讨 论:一元一次不等式组的解集
不等式组中所有不等式的解集的公共部分,叫做这个不等式组的解集.
求不等式组的解集的过程,叫做解不等式组.
知识归纳
如图分别表示一个一元一次不等式组的解集,你能分别写出不等式组的解集吗?
(2)
0
2
1
(1)
0
2
-1
(3)
0
2
-1
( )
( )
( )
( )
(4)
0
2
-1
x > 2
x < 1
-1≤ x < 2
无解
交流讨论
例1.利用数轴确定不等式组 的解集:
x<-1, ①
x≤2. ②
所以,不等式组的解集是x < -1 。
0
2
-1
例题讲解
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
②
④
①
③
-2 -1 0 1 2
议一议: (用数轴来解释)
在① ② ③ ④
各个一元一次不等式组中,两个不等式里x的值,
有公共部分的是: ;
没有公共部分的是: .
由于不等式组中的两个不等式的解集没有公共部分,此时我们称这个不等式组无解.
-5
-2
0
-3
-1
-4
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
借助数轴求下列不等式组的解集:
同大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
借助数轴求下列不等式组的解集:
同小取小
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
借助数轴求下列不等式组的解集:
大小小大中间找
借助数轴求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小解不了
练习:借助数轴求下列不等式组的解集:
练习:借助数轴求下列不等式组的解集:
能力提升:
1、一元一次不等式组 的解集是什么?
能力提升:
2、若不等式组
有解,求a的取值范围.
能力提升:
3、若不等式组
的解集为
.
的取值范围是
则
小结思考
1、什么是一元一次不等式组?
2、什么是不等式组的解集?
3、怎样解不等式组?
4、如何借助数轴确定不等式组的解集?
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
