鲁教版数学七年级下册 10.2 等腰三角形 第2课时 课件(共16张PPT)
文档属性
| 名称 | 鲁教版数学七年级下册 10.2 等腰三角形 第2课时 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
2 等腰三角形(第2课时)
1、掌握证明的基本步骤和书写格式。
2、会证明和应用等腰三角形的相关结论。
3、会证明和应用等边三角形的性质定理。
1.等腰三角形的性质是什么?
2.等边三角形有哪些性质?
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线
例1. 证明: 等腰三角形两底角的平分线相等.
求证:BD=CE.
证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵∠1= ∠ABC,∠2= ∠ACB,
∴∠1=∠2.
在△BDC和△CEB中,
∵∠ACB=∠ABC,BC=CB,∠1=∠2.
∴△BDC≌△CEB(ASA).
∴BD=CE(全等三角形的对应边相等).
2
1
E
D
C
B
A
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.
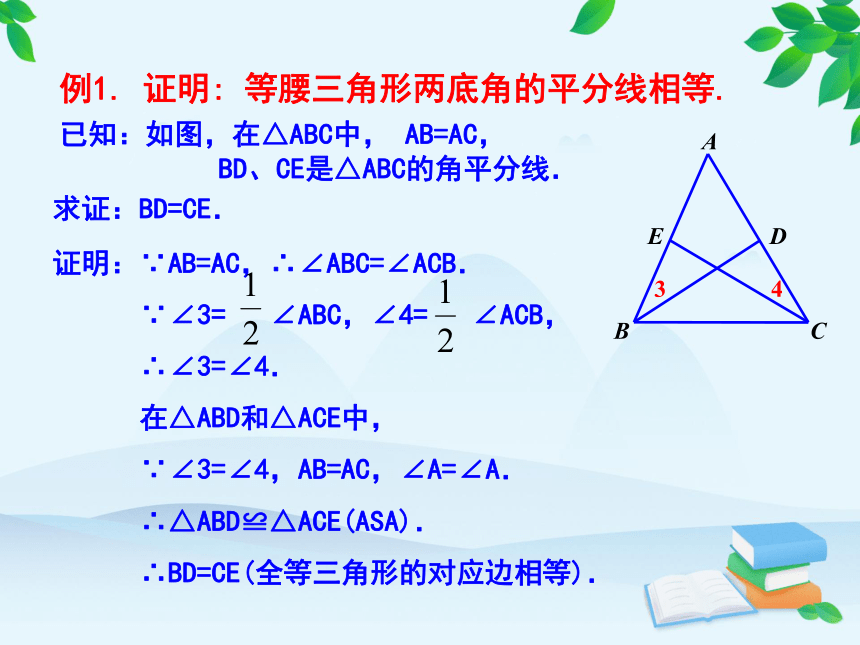
例1. 证明: 等腰三角形两底角的平分线相等.
求证:BD=CE.
4
3
E
D
C
B
A
证明:∵AB=AC,∴∠ABC=∠ACB.
∵∠3= ∠ABC,∠4= ∠ACB,
∴∠3=∠4.
在△ABD和△ACE中,
∵∠3=∠4,AB=AC,∠A=∠A.
∴△ABD≌△ACE(ASA).
∴BD=CE(全等三角形的对应边相等).
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的高.
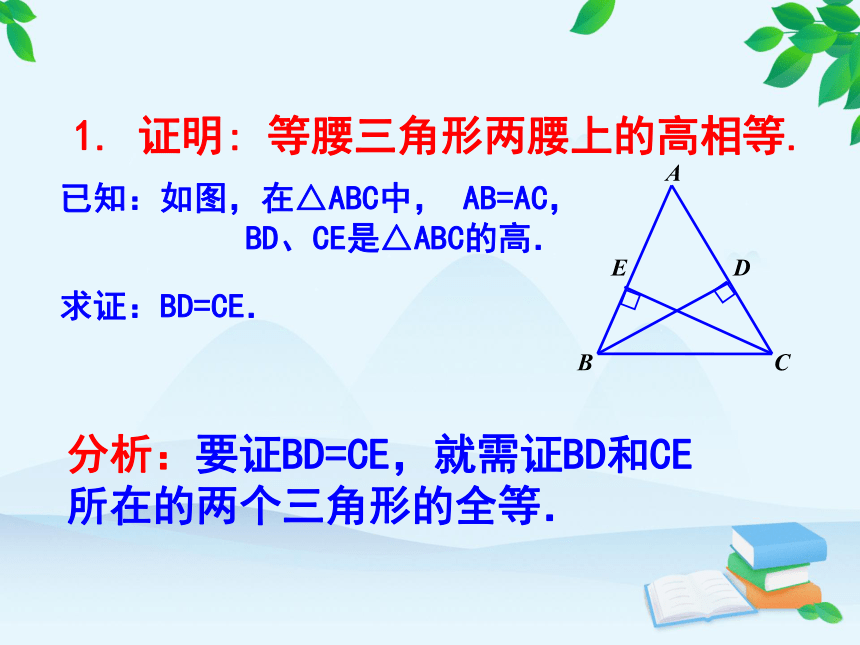
1. 证明: 等腰三角形两腰上的高相等.
求证:BD=CE.
E
D
C
B
A
分析:要证BD=CE,就需证BD和CE 所在的两个三角形的全等.
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的中线.
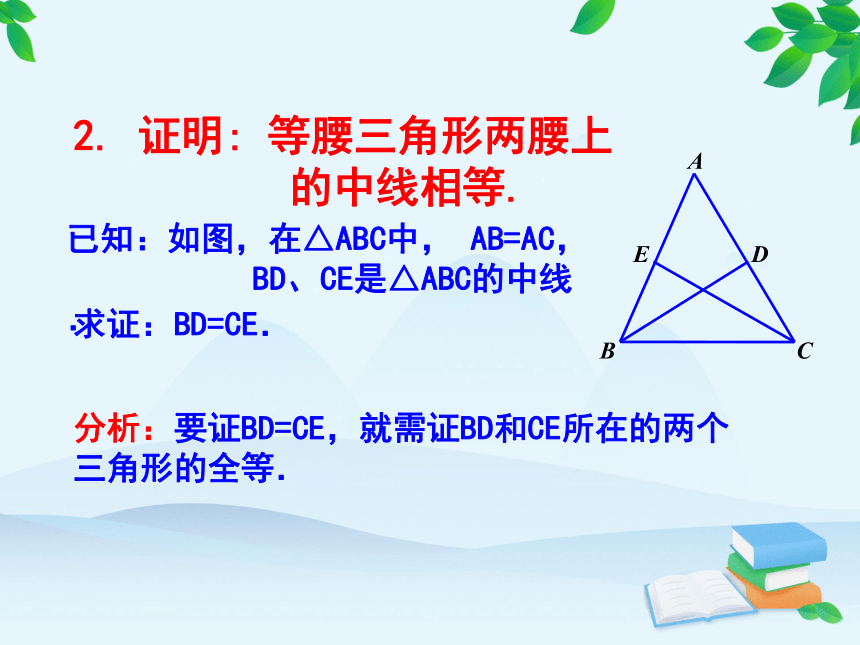
2. 证明: 等腰三角形两腰上
的中线相等.
求证:BD=CE.
E
D
C
B
A
分析:要证BD=CE,就需证BD和CE所在的两个三角形的全等.
刚才,我们只是发现并证明了等腰三角形中比较特殊的线段(角平分线、中线、高)相等
1.在等腰三角形ABC中,
(1)如果∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE吗 如果∠ABD= ∠ABC,∠ACE= ∠ACB呢 由此,你能得到一个什么结论
(2)如果AD= AC,AE= AB,那么BD=CE吗
如果AD= AC,AE= AB呢 由此你得到什么结论
(1)在△ABC中,如果AB=AC,∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE.
(2)在△ABC中,如果AB=AC,AD= AC,
AE= AB,那么BD=CE.
简述为:
(1)在△ABC中,如果AB=AC,∠ABD=∠ACE,
那么:BD=CE.
(2)在△ABC中,如果AB=AC,AD=AE,那么BD=CE.
想一想:
等边三角形都具有哪些性质?
1. 求证:等边三角形三个内角都相等并且每个内角都等于60°.
已知:如图,在△ABC中,AB=BC=AC。
求证:∠A=∠B=∠C=60°.
证明:在ΔABC中,∵AB=AC,
∴∠B=∠C(等边对等角).
同理:∠C=∠A,
∴∠A=∠B=∠C(等量代换).
又∵∠A+∠B+∠C=180°(三角形内角和定理)
∴∠A=∠B=∠C=60°.
C
B
A
1.如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
A
B
C
D
E
证明:
∵ △ABC和△BDE都是等边三角形
∴AB=BC,∠ABC=∠DBE=60°,BE=BD
∴ △ABE≌△CBD
∴AE=CD
例2、已知:如图,P、Q是△ABC的边BC上的两点,并PB=PQ=QC=AP=AQ,
求∠BAC的大小.
例3、如图,已知△ABC是等边三角形,P是BC上一点,问在CA和AB上是否存在点Q和R,使△PQR为等边三角形?若存在,求出点Q和R,并加以证明;若不存在.请说明理由.
A
P
B
C
●
●
Q
●
R
通过本节课的学习,你有哪些收获?
等 腰 三 角 形
等边三角形性质定理
等边三角形的判定方法
2 等腰三角形(第2课时)
1、掌握证明的基本步骤和书写格式。
2、会证明和应用等腰三角形的相关结论。
3、会证明和应用等边三角形的性质定理。
1.等腰三角形的性质是什么?
2.等边三角形有哪些性质?
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线
例1. 证明: 等腰三角形两底角的平分线相等.
求证:BD=CE.
证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵∠1= ∠ABC,∠2= ∠ACB,
∴∠1=∠2.
在△BDC和△CEB中,
∵∠ACB=∠ABC,BC=CB,∠1=∠2.
∴△BDC≌△CEB(ASA).
∴BD=CE(全等三角形的对应边相等).
2
1
E
D
C
B
A
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.
例1. 证明: 等腰三角形两底角的平分线相等.
求证:BD=CE.
4
3
E
D
C
B
A
证明:∵AB=AC,∴∠ABC=∠ACB.
∵∠3= ∠ABC,∠4= ∠ACB,
∴∠3=∠4.
在△ABD和△ACE中,
∵∠3=∠4,AB=AC,∠A=∠A.
∴△ABD≌△ACE(ASA).
∴BD=CE(全等三角形的对应边相等).
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的高.
1. 证明: 等腰三角形两腰上的高相等.
求证:BD=CE.
E
D
C
B
A
分析:要证BD=CE,就需证BD和CE 所在的两个三角形的全等.
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的中线.
2. 证明: 等腰三角形两腰上
的中线相等.
求证:BD=CE.
E
D
C
B
A
分析:要证BD=CE,就需证BD和CE所在的两个三角形的全等.
刚才,我们只是发现并证明了等腰三角形中比较特殊的线段(角平分线、中线、高)相等
1.在等腰三角形ABC中,
(1)如果∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE吗 如果∠ABD= ∠ABC,∠ACE= ∠ACB呢 由此,你能得到一个什么结论
(2)如果AD= AC,AE= AB,那么BD=CE吗
如果AD= AC,AE= AB呢 由此你得到什么结论
(1)在△ABC中,如果AB=AC,∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE.
(2)在△ABC中,如果AB=AC,AD= AC,
AE= AB,那么BD=CE.
简述为:
(1)在△ABC中,如果AB=AC,∠ABD=∠ACE,
那么:BD=CE.
(2)在△ABC中,如果AB=AC,AD=AE,那么BD=CE.
想一想:
等边三角形都具有哪些性质?
1. 求证:等边三角形三个内角都相等并且每个内角都等于60°.
已知:如图,在△ABC中,AB=BC=AC。
求证:∠A=∠B=∠C=60°.
证明:在ΔABC中,∵AB=AC,
∴∠B=∠C(等边对等角).
同理:∠C=∠A,
∴∠A=∠B=∠C(等量代换).
又∵∠A+∠B+∠C=180°(三角形内角和定理)
∴∠A=∠B=∠C=60°.
C
B
A
1.如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
A
B
C
D
E
证明:
∵ △ABC和△BDE都是等边三角形
∴AB=BC,∠ABC=∠DBE=60°,BE=BD
∴ △ABE≌△CBD
∴AE=CD
例2、已知:如图,P、Q是△ABC的边BC上的两点,并PB=PQ=QC=AP=AQ,
求∠BAC的大小.
例3、如图,已知△ABC是等边三角形,P是BC上一点,问在CA和AB上是否存在点Q和R,使△PQR为等边三角形?若存在,求出点Q和R,并加以证明;若不存在.请说明理由.
A
P
B
C
●
●
Q
●
R
通过本节课的学习,你有哪些收获?
等 腰 三 角 形
等边三角形性质定理
等边三角形的判定方法
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
