鲁教版数学七年级下册 10.3 直角三角形 课件(共19张PPT)
文档属性
| 名称 | 鲁教版数学七年级下册 10.3 直角三角形 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 07:25:31 | ||
图片预览





文档简介
(共19张PPT)
3 直角三角形
1、会用尺规作出已知一直角边和斜边的直角三角形;
2、能通过探索掌握直角三角形全等的判定定理(HL);
3、经历“观察--实验--猜想—验证”的过程,学会研究数学的方法。
学习目标:
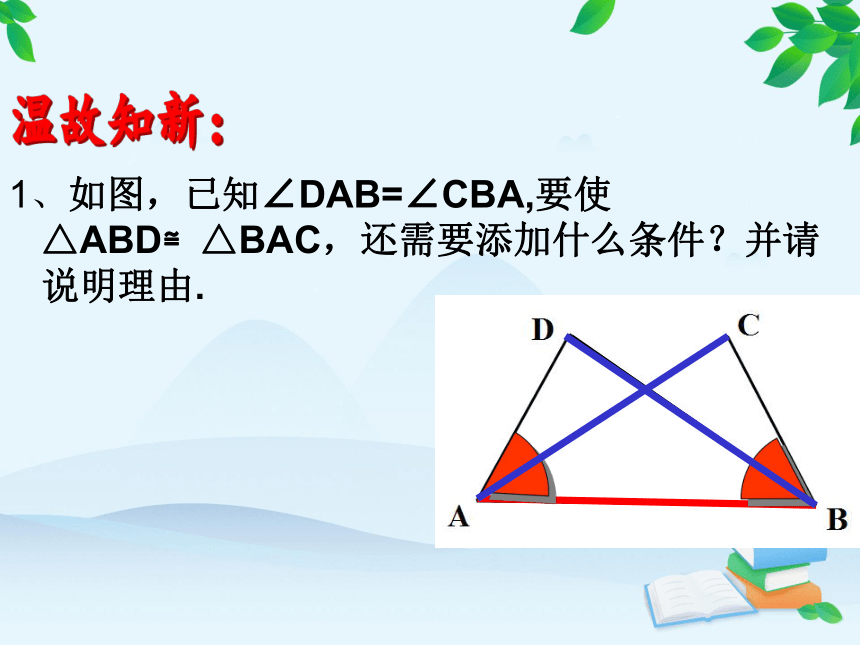
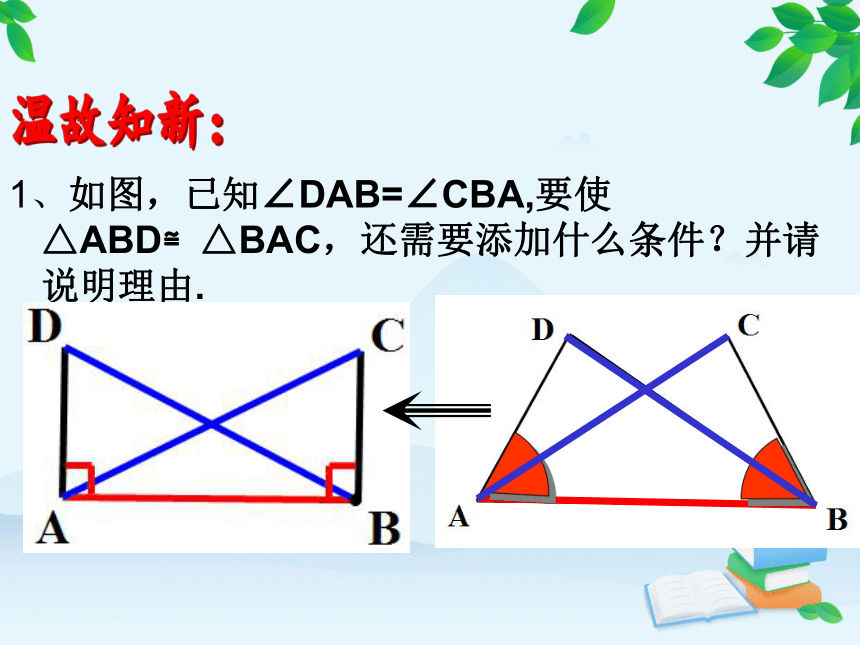
1、如图,已知∠DAB=∠CBA,要使△ABD≌△BAC,还需要添加什么条件?并请说明理由.
(1)添加:AD=BC (SAS)
(2)添加:∠D= ∠ C (AAS)
(3)添加:∠DBA= ∠ CAB
(ASA)
温故知新:
1、如图,已知∠DAB=∠CBA,要使△ABD≌△BAC,还需要添加什么条件?并请说明理由.
温故知新:
1、如图,已知∠DAB=∠CBA,要使△ABD≌△BAC,还需要添加什么条件?并请说明理由.
温故知新:
温故知新:
已知:如图,已知两线段,其长分别为 ,及直角 ,
求作:Rt△ABC,使∠C= ,BC= ,AB= .
探索发现:
2cm
3cm
小组内部交流:你们所画三角形的大小和形状有何关系,你能说明理由吗?
猜想验证:
1、问题:上题中如果, 分别取其他长度,且满足
> ,那么刚才的结论还成立吗?由此,你是否能发现判定直角三角形全等的一种特有的方法呢?可以归纳为:________________________________
小组交流并证明此命题的正确性。
斜边和一条直角边分别相等的两个直角三角形全等。
猜想验证:
已知:如图,在△ABC和△ A'B'C'中,∠C=∠ C ' =90°,
AB= A'B' = c,BC=B'C '=a.
求证: △ABC≌△ A'B'C'
4、如图2,已知AB=AD,那么添加下列条件后,
仍无法判定△ABC≌△ADC的是( )
A、CB=CD B、∠BAC=∠DAC
C、 ∠B=∠D=90° D、∠BCA=∠DCA
图2
D
(SSS)
(SAS)
(HL)
新知应用:
例:如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
新知应用:
例:如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
新知应用:
例:已知:如图,在 和 中, 、 分别是高,并且 , , 。
求证: ≌
发散探究:
例:已知:如图,在 和 中, 、 分别是高,并且 , , 。
求证: ≌
发散探究:
变式1:若把例题中的
改为 , 和 仍
全等吗?请说明思路。
例:已知:如图,在 和 中, 、 分别是高,并且 , , 。
求证: ≌
发散探究:
变式2:若把例题中的
改为 , 和 仍
全等吗?请说明思路。
例:已知:如图,在 和 中, 、 分别是高,并且 , , 。
求证: ≌
发散探究:
变式3:若把例题中的
改为另一个适当条件, 和
仍全等吗?请说明思路。
达标测评:
1、如图1,在△ABC和△ABD中,∠C=∠D =90°,要根据“HL”定理使△ABC≌△ABD成立,还需要添加的条件是( )
A、∠BAC=∠BAD B、BC=BD或AC=AD
C、∠BAC=∠BAD D、AB为公共边
2、已知:如图2,点D是△ABC中BC边上的中点,
DE⊥AC,DF⊥AB,垂足分别为E、F,且DE=DF.
求证:△ABC是等腰三角形.
图1
总结梳理:
1、尺规作图 ——— 已知斜边和一直角边作直角三角形。
2、用“HL”来验证两直角三角形全等,总结直角三角形全等判定全等的所有方法。
3、学法:“观察—实验—猜想—验证”
课外拓展:
2、勾股定理是几何中的一个重要定理,在我国古算
书《周髀算经》中就有“若勾三,股四,则弦五”的
记载.图①是由边长相等的小正方形和直角三角形构
成,可以由其面积关系验证勾股定理.图②是由图①
放入长方形内得到的,∠BAC=90°,AB=3,AC=4,
点D、E、F、G、H、I都在长方形KLMJ的边上,则长方形KLMJ的面积为( )A、90 B、100 C、110 D、121
3 直角三角形
1、会用尺规作出已知一直角边和斜边的直角三角形;
2、能通过探索掌握直角三角形全等的判定定理(HL);
3、经历“观察--实验--猜想—验证”的过程,学会研究数学的方法。
学习目标:
1、如图,已知∠DAB=∠CBA,要使△ABD≌△BAC,还需要添加什么条件?并请说明理由.
(1)添加:AD=BC (SAS)
(2)添加:∠D= ∠ C (AAS)
(3)添加:∠DBA= ∠ CAB
(ASA)
温故知新:
1、如图,已知∠DAB=∠CBA,要使△ABD≌△BAC,还需要添加什么条件?并请说明理由.
温故知新:
1、如图,已知∠DAB=∠CBA,要使△ABD≌△BAC,还需要添加什么条件?并请说明理由.
温故知新:
温故知新:
已知:如图,已知两线段,其长分别为 ,及直角 ,
求作:Rt△ABC,使∠C= ,BC= ,AB= .
探索发现:
2cm
3cm
小组内部交流:你们所画三角形的大小和形状有何关系,你能说明理由吗?
猜想验证:
1、问题:上题中如果, 分别取其他长度,且满足
> ,那么刚才的结论还成立吗?由此,你是否能发现判定直角三角形全等的一种特有的方法呢?可以归纳为:________________________________
小组交流并证明此命题的正确性。
斜边和一条直角边分别相等的两个直角三角形全等。
猜想验证:
已知:如图,在△ABC和△ A'B'C'中,∠C=∠ C ' =90°,
AB= A'B' = c,BC=B'C '=a.
求证: △ABC≌△ A'B'C'
4、如图2,已知AB=AD,那么添加下列条件后,
仍无法判定△ABC≌△ADC的是( )
A、CB=CD B、∠BAC=∠DAC
C、 ∠B=∠D=90° D、∠BCA=∠DCA
图2
D
(SSS)
(SAS)
(HL)
新知应用:
例:如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
新知应用:
例:如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
新知应用:
例:已知:如图,在 和 中, 、 分别是高,并且 , , 。
求证: ≌
发散探究:
例:已知:如图,在 和 中, 、 分别是高,并且 , , 。
求证: ≌
发散探究:
变式1:若把例题中的
改为 , 和 仍
全等吗?请说明思路。
例:已知:如图,在 和 中, 、 分别是高,并且 , , 。
求证: ≌
发散探究:
变式2:若把例题中的
改为 , 和 仍
全等吗?请说明思路。
例:已知:如图,在 和 中, 、 分别是高,并且 , , 。
求证: ≌
发散探究:
变式3:若把例题中的
改为另一个适当条件, 和
仍全等吗?请说明思路。
达标测评:
1、如图1,在△ABC和△ABD中,∠C=∠D =90°,要根据“HL”定理使△ABC≌△ABD成立,还需要添加的条件是( )
A、∠BAC=∠BAD B、BC=BD或AC=AD
C、∠BAC=∠BAD D、AB为公共边
2、已知:如图2,点D是△ABC中BC边上的中点,
DE⊥AC,DF⊥AB,垂足分别为E、F,且DE=DF.
求证:△ABC是等腰三角形.
图1
总结梳理:
1、尺规作图 ——— 已知斜边和一直角边作直角三角形。
2、用“HL”来验证两直角三角形全等,总结直角三角形全等判定全等的所有方法。
3、学法:“观察—实验—猜想—验证”
课外拓展:
2、勾股定理是几何中的一个重要定理,在我国古算
书《周髀算经》中就有“若勾三,股四,则弦五”的
记载.图①是由边长相等的小正方形和直角三角形构
成,可以由其面积关系验证勾股定理.图②是由图①
放入长方形内得到的,∠BAC=90°,AB=3,AC=4,
点D、E、F、G、H、I都在长方形KLMJ的边上,则长方形KLMJ的面积为( )A、90 B、100 C、110 D、121
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
