苏科版七年级数学下册 11.6 一元一次不等式组 教案
文档属性
| 名称 | 苏科版七年级数学下册 11.6 一元一次不等式组 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 108.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览


文档简介
课题11.6 一元一次不等式组(1)
【教学目标】
1.理解一元一次不等式组和它的解集的概念;
2.会用数轴确定一元一次不等式组的解集.
【重点难点】
重点及难点:确定两个不等式解集的公共部分;
【自主学习】 读一读:阅读课本P134-P135
【教学过程】
【温故知新】口答:求下列不等式的解集
① x-1>0 ②-4x>1
③ 1/3x<-3 ④-6x>0
⑤ -8x<-8 ⑥1-x<2
【设计意图】回顾解一元一次不等式解集的方法,为解一元一次不等式组做铺垫。
思考:设物体A的质量为x克,每个砝码的质量为1克
如图,物体A 的质量x的取值范围是什么
【设计意图】通过实际问题引入一元一次不等式组的概念。
【新知归纳】
1. 像这样,由几个含有同一未知数的一次不等式组成的不等式组叫做一元一次不等式组。
【火眼金睛】下列各式中哪些是一元一次不等式组?(学生口答)
注:不等式组中各不等式所含未知数必须相同且代表同一个量
【设计意图】明确一元一次不等式组的概念,辨析一元一次不等式组。
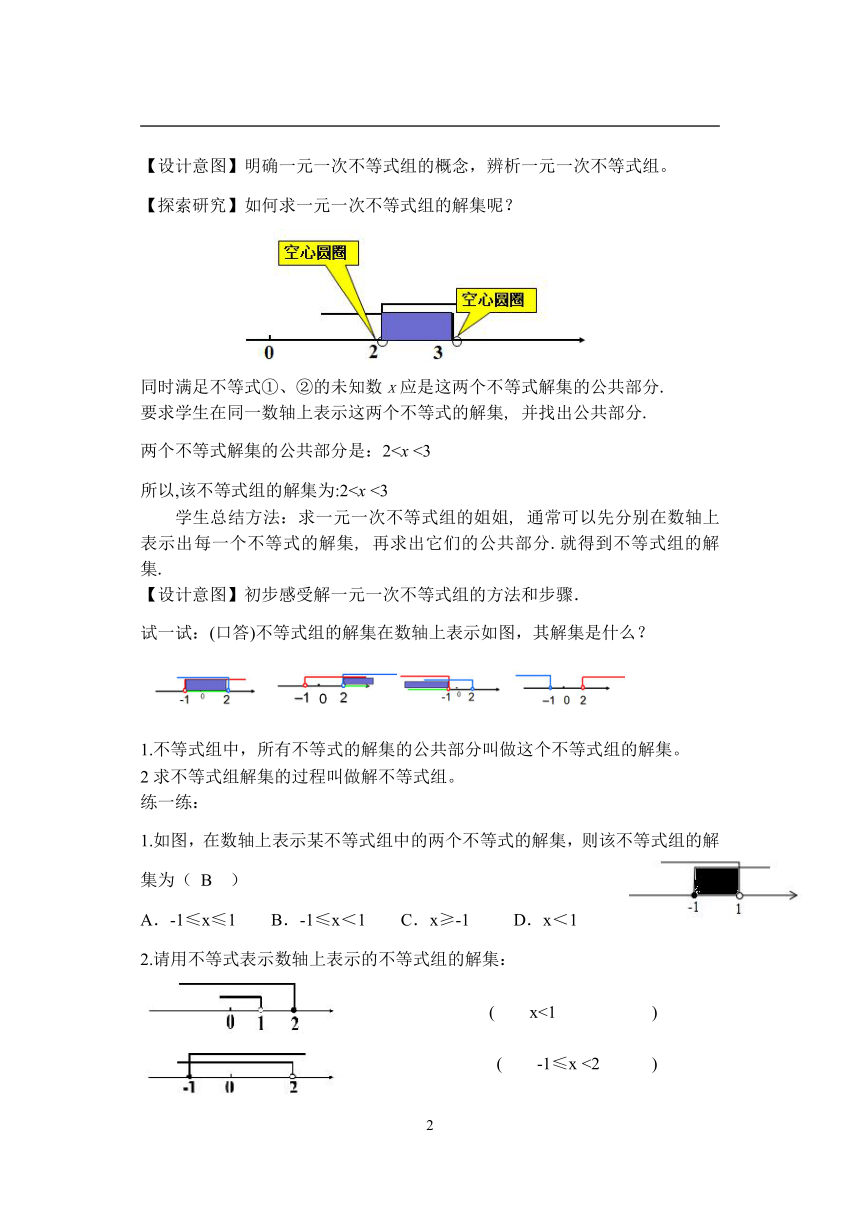
【探索研究】如何求一元一次不等式组的解集呢?
同时满足不等式①、②的未知数x应是这两个不等式解集的公共部分.
要求学生在同一数轴上表示这两个不等式的解集, 并找出公共部分.
两个不等式解集的公共部分是:2所以,该不等式组的解集为:2学生总结方法:求一元一次不等式组的姐姐, 通常可以先分别在数轴上表示出每一个不等式的解集, 再求出它们的公共部分.就得到不等式组的解集.
【设计意图】初步感受解一元一次不等式组的方法和步骤.
试一试:(口答)不等式组的解集在数轴上表示如图,其解集是什么?
1.不等式组中,所有不等式的解集的公共部分叫做这个不等式组的解集。
2求不等式组解集的过程叫做解不等式组。
练一练:
1.如图,在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为( B )
A.-1≤x≤1 B.-1≤x<1 C.x≥-1 D.x<1
2.请用不等式表示数轴上表示的不等式组的解集:
( x<1 )
( -1≤x <2 )
【设计意图】尝试通过数轴找出不等式解集的公共部分。
【例题教学】
例 1 .利用数轴确定下列不等式组的解集:
(1) (2)
(3) (4)
解:(教师板书示范)
【设计意图】学生尝试独立解不等式组,老师强调规范格式。
交流讨论——见课件PPT
【设计意图】进一步感受找出不等式解集的公共部分,就是不等式组的解集。
学生归纳,教师总结:
一元一次不等式组解集四种类型如下表:
不等式组(a<b 数轴表示 解 集 记忆口诀
(1) (
a
b
) x>b 同大取大
(2) (
a
b
) x<a 同小取小
(3) (
a
b
) a<x<b 大小小大中间找
(4) (
a
b
) 无解 大大小小无解
比一比:看谁反应快
运用口诀求下列不等式组的解集
【设计意图】进一步熟练找出不等式组的解集。
例 2 .B组:求不等式组 的负整数解。
A组: 如果一元一次不等式组的解集为x>3,则a的取值范围为 ________________
【设计意图】分层布置例题,进一步强化数形结合求不等式组解集的必要性。
【课堂检测】
1. 不等式组的解集在数轴上可以表示为( )
(A) (B) (C) (D)
2. 一元一次不等式组的解集是 ;
3.利用数轴确定下列不等式组的解集:
(1) (2)
(3) (4)
4.B组:不等式组的整数解是_____________
A 组:回答下列问题:
(1)若不等式组无解,则a的取值范围是________________.
(2)若该不等式组 有解,则a的取值范围是________________.
(3)若该不等式组 有3个整数解,则a的取值范围是_____________.
【设计意图】通过课堂检测,及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整
【课后作业】
1. 如图,数轴上表示的是下列哪个不等式组的解集( )
2.写出一个解集为x<-2的一元一次不等式组_______________________.
3. B组:若不等式组有解,则m的取值范围是____________________.
A组:.如果一元一次不等式组的解集为x>3,则a的取值范围为_____.
4. 利用数轴确定下列不等式组的解集:
(1) (2)
(3) (4)
【课后反思】
从学生学习的心理基础和认知特点来说,学生已经学习了一元一次不等式,并能较熟练地解一元一次不等式,能将简单的实际问题抽象为数学模型,有一定的数学化能力。但学生将两个一元一次不等式的解集在同一数轴上表示会产生一定的困惑。这个年龄段的学生,以感性认识为主,并向理性认知过渡,所以,我对本节课的设计是通过一个学生所熟悉的问题情境,让学生独立思考,合作交流,从而引导其自主学习。基于对学情的分析,我确定了本节课的教学难点是:正确理解不等式组的解集。为了化解重难点,通过实例让学生体会一元一次不等式组是研究量与量之间关系的重要模型之一,培养学生分析、解决实际问题的能力。通过画数轴寻找不等式组解集的公共部分,确立不等式组的解集。
本节课课堂上学生动手画数轴的时间略显不足,所以对于不等式组解集的口诀还不是太熟练,课堂气氛上略显沉闷,形式应该更活泼,多样化一些会更好。
4
【教学目标】
1.理解一元一次不等式组和它的解集的概念;
2.会用数轴确定一元一次不等式组的解集.
【重点难点】
重点及难点:确定两个不等式解集的公共部分;
【自主学习】 读一读:阅读课本P134-P135
【教学过程】
【温故知新】口答:求下列不等式的解集
① x-1>0 ②-4x>1
③ 1/3x<-3 ④-6x>0
⑤ -8x<-8 ⑥1-x<2
【设计意图】回顾解一元一次不等式解集的方法,为解一元一次不等式组做铺垫。
思考:设物体A的质量为x克,每个砝码的质量为1克
如图,物体A 的质量x的取值范围是什么
【设计意图】通过实际问题引入一元一次不等式组的概念。
【新知归纳】
1. 像这样,由几个含有同一未知数的一次不等式组成的不等式组叫做一元一次不等式组。
【火眼金睛】下列各式中哪些是一元一次不等式组?(学生口答)
注:不等式组中各不等式所含未知数必须相同且代表同一个量
【设计意图】明确一元一次不等式组的概念,辨析一元一次不等式组。
【探索研究】如何求一元一次不等式组的解集呢?
同时满足不等式①、②的未知数x应是这两个不等式解集的公共部分.
要求学生在同一数轴上表示这两个不等式的解集, 并找出公共部分.
两个不等式解集的公共部分是:2
【设计意图】初步感受解一元一次不等式组的方法和步骤.
试一试:(口答)不等式组的解集在数轴上表示如图,其解集是什么?
1.不等式组中,所有不等式的解集的公共部分叫做这个不等式组的解集。
2求不等式组解集的过程叫做解不等式组。
练一练:
1.如图,在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为( B )
A.-1≤x≤1 B.-1≤x<1 C.x≥-1 D.x<1
2.请用不等式表示数轴上表示的不等式组的解集:
( x<1 )
( -1≤x <2 )
【设计意图】尝试通过数轴找出不等式解集的公共部分。
【例题教学】
例 1 .利用数轴确定下列不等式组的解集:
(1) (2)
(3) (4)
解:(教师板书示范)
【设计意图】学生尝试独立解不等式组,老师强调规范格式。
交流讨论——见课件PPT
【设计意图】进一步感受找出不等式解集的公共部分,就是不等式组的解集。
学生归纳,教师总结:
一元一次不等式组解集四种类型如下表:
不等式组(a<b 数轴表示 解 集 记忆口诀
(1) (
a
b
) x>b 同大取大
(2) (
a
b
) x<a 同小取小
(3) (
a
b
) a<x<b 大小小大中间找
(4) (
a
b
) 无解 大大小小无解
比一比:看谁反应快
运用口诀求下列不等式组的解集
【设计意图】进一步熟练找出不等式组的解集。
例 2 .B组:求不等式组 的负整数解。
A组: 如果一元一次不等式组的解集为x>3,则a的取值范围为 ________________
【设计意图】分层布置例题,进一步强化数形结合求不等式组解集的必要性。
【课堂检测】
1. 不等式组的解集在数轴上可以表示为( )
(A) (B) (C) (D)
2. 一元一次不等式组的解集是 ;
3.利用数轴确定下列不等式组的解集:
(1) (2)
(3) (4)
4.B组:不等式组的整数解是_____________
A 组:回答下列问题:
(1)若不等式组无解,则a的取值范围是________________.
(2)若该不等式组 有解,则a的取值范围是________________.
(3)若该不等式组 有3个整数解,则a的取值范围是_____________.
【设计意图】通过课堂检测,及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整
【课后作业】
1. 如图,数轴上表示的是下列哪个不等式组的解集( )
2.写出一个解集为x<-2的一元一次不等式组_______________________.
3. B组:若不等式组有解,则m的取值范围是____________________.
A组:.如果一元一次不等式组的解集为x>3,则a的取值范围为_____.
4. 利用数轴确定下列不等式组的解集:
(1) (2)
(3) (4)
【课后反思】
从学生学习的心理基础和认知特点来说,学生已经学习了一元一次不等式,并能较熟练地解一元一次不等式,能将简单的实际问题抽象为数学模型,有一定的数学化能力。但学生将两个一元一次不等式的解集在同一数轴上表示会产生一定的困惑。这个年龄段的学生,以感性认识为主,并向理性认知过渡,所以,我对本节课的设计是通过一个学生所熟悉的问题情境,让学生独立思考,合作交流,从而引导其自主学习。基于对学情的分析,我确定了本节课的教学难点是:正确理解不等式组的解集。为了化解重难点,通过实例让学生体会一元一次不等式组是研究量与量之间关系的重要模型之一,培养学生分析、解决实际问题的能力。通过画数轴寻找不等式组解集的公共部分,确立不等式组的解集。
本节课课堂上学生动手画数轴的时间略显不足,所以对于不等式组解集的口诀还不是太熟练,课堂气氛上略显沉闷,形式应该更活泼,多样化一些会更好。
4
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
