轴对称图形单元测试

第一章 轴对称图形
一、选择题
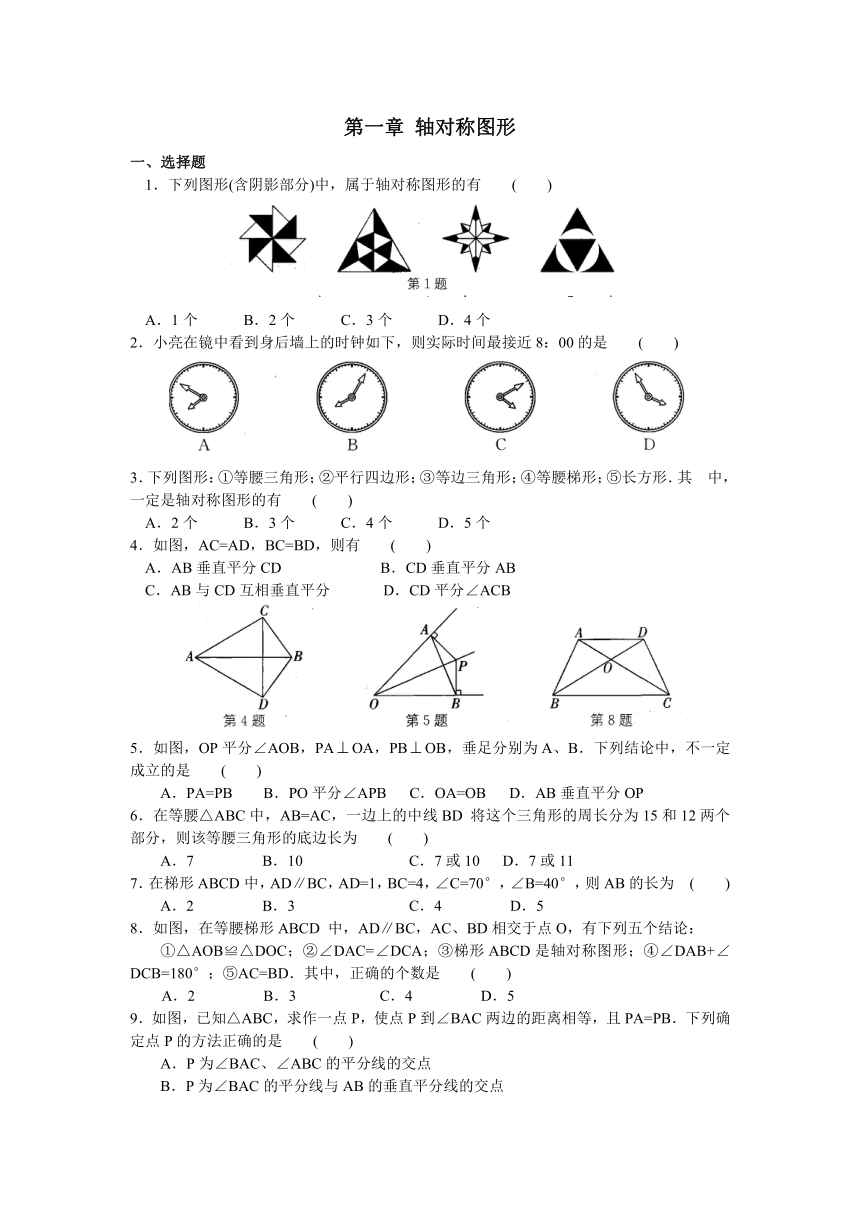
1．下列图形(含阴影部分)中，属于轴对称图形的有 ( )
A．1个 B．2个 C．3个 D．4个
2．小亮在镜中看到身后墙上的时钟如下，则实际时间最接近8：00的是 ( )
3．下列图形：①等腰三角形；②平行四边形；③等边三角形；④等腰梯形；⑤长方形．其 中，一定是轴对称图形的有 ( )
A．2个 B．3个 C．4个 D．5个
4．如图，AC=AD，BC=BD，则有 ( )
A．AB垂直平分CD B．CD垂直平分AB
C．AB与CD互相垂直平分 D．CD平分∠ACB
5．如图，OP平分∠AOB，PAOA，PBOB，垂足分别为A、B．下列结论中，不一定成立的是 ( )
A．PA=PB B．PO平分∠APB C．OA=OB D．AB垂直平分OP
6．在等腰△ABC中，AB=AC，一边上的中线BD 将这个三角形的周长分为15和12两个部分，则该等腰三角形的底边长为 ( )
A．7 B．10 C．7或10 D．7或11
7．在梯形ABCD中，AD∥BC，AD=1，BC=4，∠C=70°，∠B=40°，则AB的长为 ( )
A．2 B．3 C．4 D．5
8．如图，在等腰梯形ABCD 中，AD∥BC，AC、BD相交于点O，有下列五个结论：
①△AOB≌△DOC；②∠DAC=∠DCA；③梯形ABCD是轴对称图形；④∠DAB+∠DCB=180°；⑤AC=BD．其中，正确的个数是 ( )
A．2 B．3 C．4 D．5
9．如图，已知△ABC，求作一点P，使点P到∠BAC两边的距离相等，且PA=PB．下列确定点P的方法正确的是 ( )
A．P为∠BAC、∠ABC的平分线的交点
B．P为∠BAC的平分线与AB的垂直平分线的交点
C．P为AC、AB两边上的高的交点
D．P为AC、AB两边的垂直平分线的交点
10．如图，在△ABC中，AD平分∠BAC，DEAB，DFAC，E、F为垂足，则下列五个结论：①∠DEF=∠DFE；②AE=AF；③AD垂直平分EF；④EF垂直平分AD；
⑤△ABD与△ACD的面积相等．其中，正确的个数是 ( )
A．4 B．3 C．2 D．1
二、填空题
11．请同学们写出两个具有轴对称性的汉字：__________．
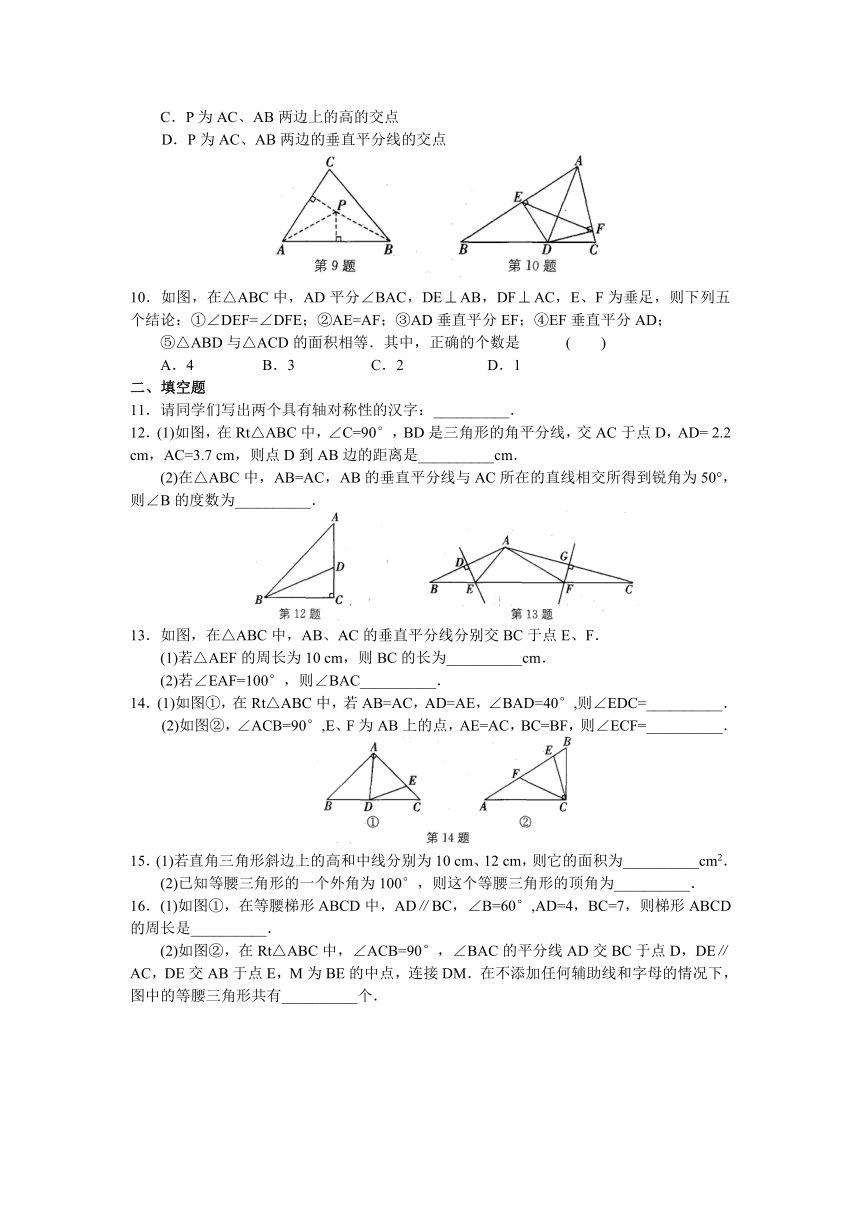
12．(1)如图，在Rt△ABC中，∠C=90°，BD是三角形的角平分线，交AC于点D，AD= 2.2 cm，AC=3.7 cm，则点D到AB边的距离是__________cm．
(2)在△ABC中，AB=AC，AB的垂直平分线与AC所在的直线相交所得到锐角为50°，则∠B的度数为__________．
13．如图，在△ABC中，AB、AC的垂直平分线分别交BC于点E、F．
(1)若△AEF的周长为10 cm，则BC的长为__________cm．
(2)若∠EAF=100°，则∠BAC__________．
14．(1)如图①，在Rt△ABC中，若AB=AC，AD=AE，∠BAD=40°,则∠EDC=__________．
(2)如图②，∠ACB=90°,E、F为AB上的点，AE=AC，BC=BF，则∠ECF=__________．
15．(1)若直角三角形斜边上的高和中线分别为10 cm、12 cm，则它的面积为__________cm2．
(2)已知等腰三角形的一个外角为100°，则这个等腰三角形的顶角为__________．
16．(1)如图①，在等腰梯形ABCD中，AD∥BC，∠B=60°,AD=4，BC=7，则梯形ABCD的周长是__________．
(2)如图②，在Rt△ABC中，∠ACB=90°，∠BAC的平分线AD交BC于点D，DE∥AC，DE交AB于点E，M为BE的中点，连接DM．在不添加任何辅助线和字母的情况下，图中的等腰三角形共有__________个．
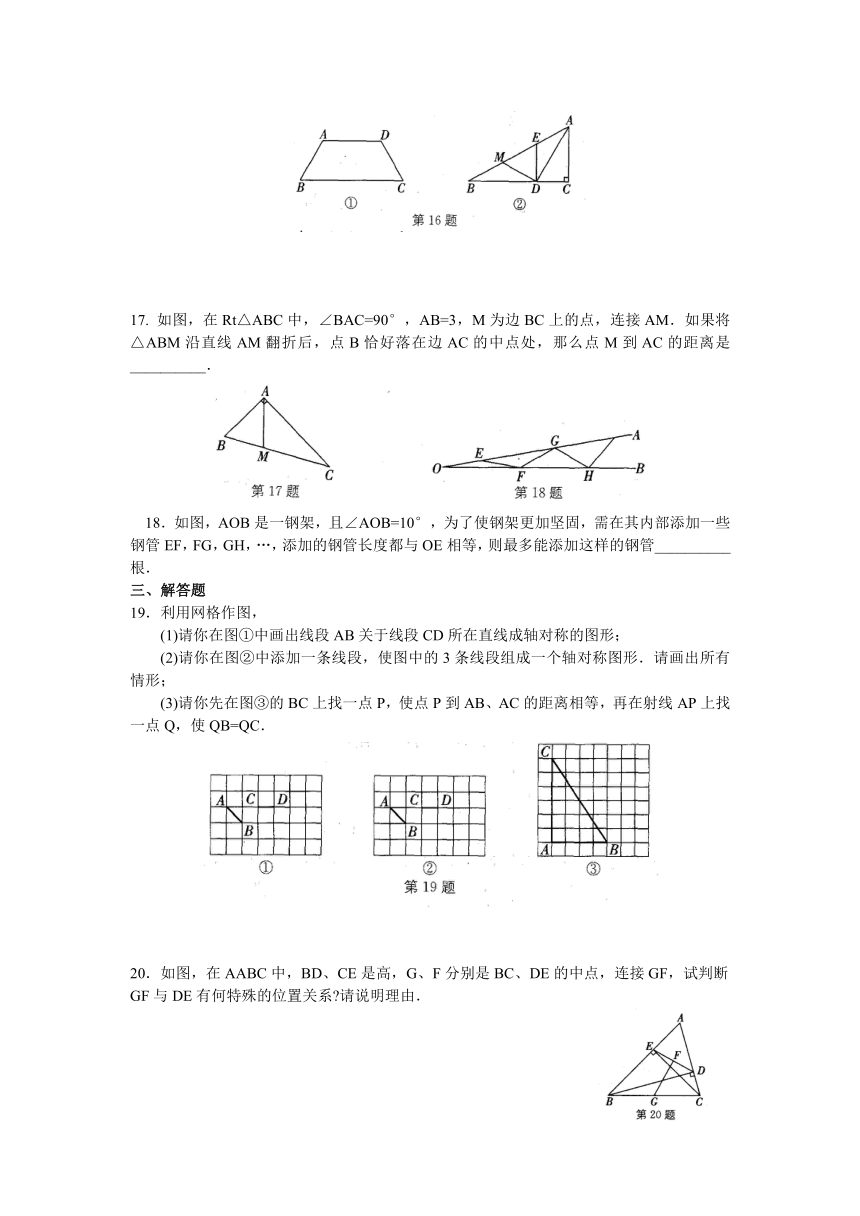
17. 如图，在Rt△ABC中，∠BAC=90°，AB=3，M为边BC上的点，连接AM．如果将△ABM沿直线AM翻折后，点B恰好落在边AC的中点处，那么点M到AC的距离是__________．
18．如图，AOB是一钢架，且∠AOB=10°，为了使钢架更加坚固，需在其内部添加一些钢管EF，FG，GH，…，添加的钢管长度都与OE相等，则最多能添加这样的钢管__________根．
三、解答题
19．利用网格作图，
(1)请你在图①中画出线段AB关于线段CD所在直线成轴对称的图形；
(2)请你在图②中添加一条线段，使图中的3条线段组成一个轴对称图形．请画出所有 情形；
(3)请你先在图③的BC上找一点P，使点P到AB、AC的距离相等，再在射线AP上找一点Q，使QB=QC．
20．如图，在AABC中，BD、CE是高，G、F分别是BC、DE的中点，连接GF，试判断GF与DE有何特殊的位置关系?请说明理由．

21．如图，在△ABC中，AB=AC，BC=BD=ED=EA，求∠A的度数．
22．如图，在梯形ABCD中，AD∥BC，AB=DC=AD，BC=AC，求该梯形中各内角的度数．
23．如图，在等腰△ABC中，顶角的平分线BD交AC于点D，AD=3，作△ABC的高AE交CB的延长线于点E，且AE与BC的长是方程组的解．已知，求△ABC的周长．
24．如图，在等腰梯形ABCD中，AD∥BC，AB=DC，点P为BC边上一点，PE⊥AB于点E，PF⊥DC于点F，BG⊥CD于点G，试说明PE+PF=BG．
25．在梯形ABCD中，B=90°，AB14cm，AD=18cm，BC=21cm，点P从点A开始沿边AD向点D以1 cm／s的速度移动，点Q从点C开始沿边CB向点B以2 cm／s的速度移动，如果点P、Q分别从两点同时出发，多少秒后，梯形PBQD是等腰梯形?
参考答案
一、1．B 2. D 3．C 4．A 5．D 6．D 7．B 8．C 9．B 10．B
二、11．答案不唯一，如目、田
12．(1)1.5 (2)70°或20°
13．(1)10 (2)140° 14．(1)20°(2)45° 15．(1)120 (2)80°或20°
16．(1)17 (2)3 17．2 18．8
三、19．略
20．GFDE理由：连接GE、GD．因为BD是△ABC的高，所以∠BDC=90°．因为G是BC的中点，所以DG=BC．同理，EG=BC．所以DG=EG．又因为F是DE的中点，所以在△EGD中，GFDE．
21．设∠A=x．因为AE=ED，所以∠ADE=∠A=x．又∠BED为△AED的外角，所以∠BED=∠ADE+∠A=2x．因为BD=ED，所以∠DBE=∠DEB=2x．因为∠BDC为△ABD的外角，所以∠BDC=∠EBD+∠A=3x．因为BD=BC，所以∠BDC=∠C=3x．因为AB=AC，所以∠ABC=∠C=3x．又因为△ABC的内角和为180°，所以22+3x+3x=180°．解得x=() °，即∠A=() °
22．如图，设∠1=x．因为AB=AD，所以∠1=∠2=x．因为AD∥BC，所以∠2=∠3=x．所以∠ABC=∠1+∠3=2x．因为AD∥BC，AB=DC，所以∠ABC=∠DCB=2x，AC=BD．又因为BC=AC，所以BC=BD．所以∠4=∠BCD=2x．因ABCD的内角和为180°．所以x+2x+2x=180°，解得x=36°．所以∠ABC=∠DCB=72°．因为AD∥BC，所以∠ABC+∠BAD=180°，∠DCB+∠ADC=180°，所以∠BAD=∠ADC=108°
23．由①+②得，15x=15m3．所以x=m．
①×2②得15y=15m，所以y=m．由，得xy=m，即
·(m)m=m．因为m≠0，所以，解得m=5．此时由于AB=BC＞AE，所以BC=5，AE=4.8．又因为AB=BC，BD平分∠ABC，所以AD=DC=3，即AC=6．所以△ABC的周长为6+5 x 2=16