沪科版一次函数阶段测试卷
图片预览


文档简介
一、选择题
1. 若一次函数的图象经过坐标原点,则( )
A. B.
C.或 D.无法确定
2. 下列说法中不正确的是( )
A.一次函数不一定是正比例函数 B.不是一次函数一定不是正比例函数
C.不是正比例函数,就不是一次函数 D.正比例函数是特殊的一次函数
3. 下列各题中,成正比例关系的是( )
A.货物单价一定时,货物的总价与数量
B.货物总价一定时,货物单价与数量
C.正方形的面积和它的一边长
D.中的与
4. 弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,由图可知不挂物体时弹簧的长度为( )
A. B. C. D.
5. 下列四个函数,其中自变量取值范围相同的是( )
(1)y=x+1;(2)y=)2;(3);(4)
A.(1)和(2) B.(1)和(3) C.(2)和(4) D.(1)和(4)
6. 在圆的周长公式中,下列说法错误的是( )
A.是变量,2是常量
B.是变量,是常量
C.是自变量,是的函数
D.将写成,则可看作是自变量,是的函数
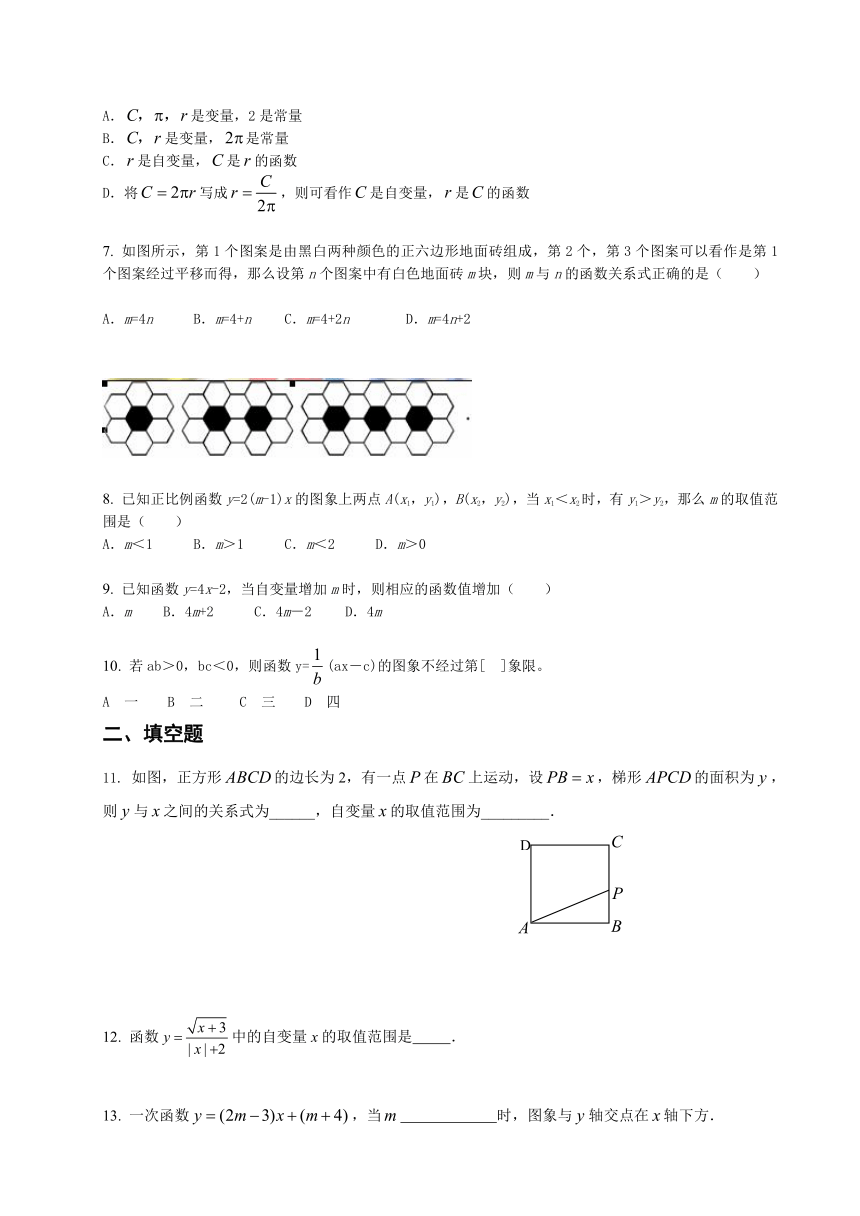
7. 如图所示,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么设第n个图案中有白色地面砖m块,则m与n的函数关系式正确的是( )
A.m=4n B.m=4+n C.m=4+2n D.m=4n+2
8. 已知正比例函数y=2(m-1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A.m<1 B.m>1 C.m<2 D.m>0
9. 已知函数y=4x-2,当自变量增加m时,则相应的函数值增加( )
A.m B.4m+2 C.4m-2 D.4m
10. 若ab>0,bc<0,则函数y=(ax-c)的图象不经过第[ ]象限。
A 一 B 二 C 三 D 四
二、填空题
11. 如图,正方形的边长为2,有一点在上运动,设,梯形的面积为,则与之间的关系式为______,自变量的取值范围为_________.
12. 函数中的自变量x的取值范围是 .
13. 一次函数,当 时,图象与轴交点在轴下方.
14. 一个函数的图象与直线平行,且与直线的交点在轴上,那么这个一次函数的解析式为 .
15. 一次函数y=kx+b的图像经过点(0,2),(3,0),若将该图像向下平移3个单位,则新图像对应的表达式为____.
16. 蜡烛在空气中燃烧的长度与时间成正比.如果一支原长15cm的蜡烛燃烧4分钟后,其长度变为13cm,请写出剩余长度y(cm)与燃烧时间x(分钟)的关系式为______.
17. x=___________时,函数y=3x-2与函数y=5x+1有相同的函数值.
18. 已知y=(k-1)x+k2-1是正比例函数,则k= .
19. 直线y=-x-2与坐标轴围成的图形的面积是___.
20. 若一次函数y1=kx-b的图象经过第一、三、四象限,则一次函数y2=bx+k的图象经过第 象限.
三、计算题
21. 已知一次函数的图象经过点P(0,-2),且与两坐标轴围成的三角形面积为3,求此一次函数的解析示.
四、应用题
22. 下图是某地一天的气温随时间变化的图像.根据这张图回答:在这一天中,
(1)什么时间气温最高?什么时间气温最低?最高气温和最低气温各是多少度?
(2)20时的气温是多少?
(3)什么时候气温为6℃?
(4)哪段时间内气温不断下降?
(5)哪段时间内气温不断上升?
(6)哪段时间内气温保持不变?
23. 已知一次函数,当时,,且它的图象与轴交点的纵坐标是,求它的解析式.
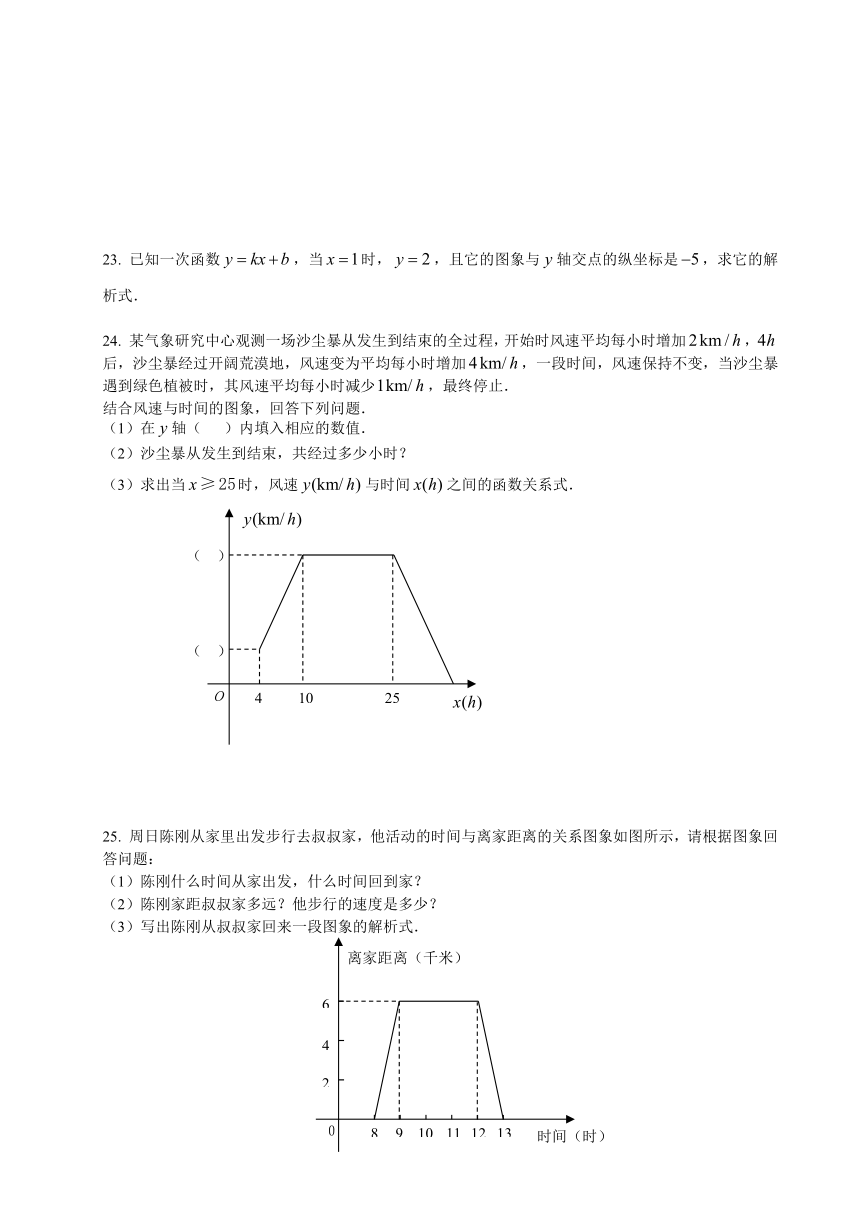
24. 某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时风速平均每小时增加,后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加,一段时间,风速保持不变,当沙尘暴遇到绿色植被时,其风速平均每小时减少,最终停止.
结合风速与时间的图象,回答下列问题.
(1)在轴( )内填入相应的数值.
(2)沙尘暴从发生到结束,共经过多少小时?
(3)求出当时,风速与时间之间的函数关系式.
25. 周日陈刚从家里出发步行去叔叔家,他活动的时间与离家距离的关系图象如图所示,请根据图象回答问题:
(1)陈刚什么时间从家出发,什么时间回到家?
(2)陈刚家距叔叔家多远?他步行的速度是多少?
(3)写出陈刚从叔叔家回来一段图象的解析式.
26. 的图像上有两点,知,你能说出与有什么关系吗?
27. 已知一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数的图象与y轴相交于点Q(0,4).
(1)求这两个函数的解析式.
(2)在同一坐标系内,分别画出这两个函数的图象.
(3)求出△POQ的面积.
28. 已知一次函数y=(6+3m)x+(n-4).
(1)当m、n为何值时,y随x的增大而减小?
(2)当m、n为何值时,函数的图象与y轴的交点在x轴的下方?
(3)当m、n为何值时,函数图象经过原点?
一、选择题
1. A
2. C
3. A
4. D
5. D
6. A
7. D
8. A
9. D
10. D
二、填空题
11. ,
12.
13.
14.
15.
16.
17. -
18.
19. ;
20. 一、二、三
三、计算题
21.
四、应用题
22. (1)16时气温最高,气温是10℃;凌晨4时,气温最低,气温是℃
(2)20时的气温是8℃
(3)10时和22时气温都是6℃
(4)0时到4时和16时到24时这两段时间内气温不断下降
(5)4时到12时和14时到16时这两段时间气温不断上升
(6)12时到14时这段时间内气温保持在8℃不变
23.
24. (1),
(2)共经过小时
(3)
25. (1)时出发,时回家,
(2)6千米,千米/时
(3)
26.
27. (1)正比例函数的解析式为.一次函数的解析式为
(2)图略;
(3)4
28. (1),为任意实数时,随的增大而减小;
(2)时,函数图象与轴的交点在轴下方;
(3)当,时,函数图象经过原点
1. 若一次函数的图象经过坐标原点,则( )
A. B.
C.或 D.无法确定
2. 下列说法中不正确的是( )
A.一次函数不一定是正比例函数 B.不是一次函数一定不是正比例函数
C.不是正比例函数,就不是一次函数 D.正比例函数是特殊的一次函数
3. 下列各题中,成正比例关系的是( )
A.货物单价一定时,货物的总价与数量
B.货物总价一定时,货物单价与数量
C.正方形的面积和它的一边长
D.中的与
4. 弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,由图可知不挂物体时弹簧的长度为( )
A. B. C. D.
5. 下列四个函数,其中自变量取值范围相同的是( )
(1)y=x+1;(2)y=)2;(3);(4)
A.(1)和(2) B.(1)和(3) C.(2)和(4) D.(1)和(4)
6. 在圆的周长公式中,下列说法错误的是( )
A.是变量,2是常量
B.是变量,是常量
C.是自变量,是的函数
D.将写成,则可看作是自变量,是的函数
7. 如图所示,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么设第n个图案中有白色地面砖m块,则m与n的函数关系式正确的是( )
A.m=4n B.m=4+n C.m=4+2n D.m=4n+2
8. 已知正比例函数y=2(m-1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A.m<1 B.m>1 C.m<2 D.m>0
9. 已知函数y=4x-2,当自变量增加m时,则相应的函数值增加( )
A.m B.4m+2 C.4m-2 D.4m
10. 若ab>0,bc<0,则函数y=(ax-c)的图象不经过第[ ]象限。
A 一 B 二 C 三 D 四
二、填空题
11. 如图,正方形的边长为2,有一点在上运动,设,梯形的面积为,则与之间的关系式为______,自变量的取值范围为_________.
12. 函数中的自变量x的取值范围是 .
13. 一次函数,当 时,图象与轴交点在轴下方.
14. 一个函数的图象与直线平行,且与直线的交点在轴上,那么这个一次函数的解析式为 .
15. 一次函数y=kx+b的图像经过点(0,2),(3,0),若将该图像向下平移3个单位,则新图像对应的表达式为____.
16. 蜡烛在空气中燃烧的长度与时间成正比.如果一支原长15cm的蜡烛燃烧4分钟后,其长度变为13cm,请写出剩余长度y(cm)与燃烧时间x(分钟)的关系式为______.
17. x=___________时,函数y=3x-2与函数y=5x+1有相同的函数值.
18. 已知y=(k-1)x+k2-1是正比例函数,则k= .
19. 直线y=-x-2与坐标轴围成的图形的面积是___.
20. 若一次函数y1=kx-b的图象经过第一、三、四象限,则一次函数y2=bx+k的图象经过第 象限.
三、计算题
21. 已知一次函数的图象经过点P(0,-2),且与两坐标轴围成的三角形面积为3,求此一次函数的解析示.
四、应用题
22. 下图是某地一天的气温随时间变化的图像.根据这张图回答:在这一天中,
(1)什么时间气温最高?什么时间气温最低?最高气温和最低气温各是多少度?
(2)20时的气温是多少?
(3)什么时候气温为6℃?
(4)哪段时间内气温不断下降?
(5)哪段时间内气温不断上升?
(6)哪段时间内气温保持不变?
23. 已知一次函数,当时,,且它的图象与轴交点的纵坐标是,求它的解析式.
24. 某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时风速平均每小时增加,后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加,一段时间,风速保持不变,当沙尘暴遇到绿色植被时,其风速平均每小时减少,最终停止.
结合风速与时间的图象,回答下列问题.
(1)在轴( )内填入相应的数值.
(2)沙尘暴从发生到结束,共经过多少小时?
(3)求出当时,风速与时间之间的函数关系式.
25. 周日陈刚从家里出发步行去叔叔家,他活动的时间与离家距离的关系图象如图所示,请根据图象回答问题:
(1)陈刚什么时间从家出发,什么时间回到家?
(2)陈刚家距叔叔家多远?他步行的速度是多少?
(3)写出陈刚从叔叔家回来一段图象的解析式.
26. 的图像上有两点,知,你能说出与有什么关系吗?
27. 已知一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数的图象与y轴相交于点Q(0,4).
(1)求这两个函数的解析式.
(2)在同一坐标系内,分别画出这两个函数的图象.
(3)求出△POQ的面积.
28. 已知一次函数y=(6+3m)x+(n-4).
(1)当m、n为何值时,y随x的增大而减小?
(2)当m、n为何值时,函数的图象与y轴的交点在x轴的下方?
(3)当m、n为何值时,函数图象经过原点?
一、选择题
1. A
2. C
3. A
4. D
5. D
6. A
7. D
8. A
9. D
10. D
二、填空题
11. ,
12.
13.
14.
15.
16.
17. -
18.
19. ;
20. 一、二、三
三、计算题
21.
四、应用题
22. (1)16时气温最高,气温是10℃;凌晨4时,气温最低,气温是℃
(2)20时的气温是8℃
(3)10时和22时气温都是6℃
(4)0时到4时和16时到24时这两段时间内气温不断下降
(5)4时到12时和14时到16时这两段时间气温不断上升
(6)12时到14时这段时间内气温保持在8℃不变
23.
24. (1),
(2)共经过小时
(3)
25. (1)时出发,时回家,
(2)6千米,千米/时
(3)
26.
27. (1)正比例函数的解析式为.一次函数的解析式为
(2)图略;
(3)4
28. (1),为任意实数时,随的增大而减小;
(2)时,函数图象与轴的交点在轴下方;
(3)当,时,函数图象经过原点
