2021--2022学年人教版八年级数学下册17.2勾股定理的逆定理课堂训练试卷(Word版含答案)
文档属性
| 名称 | 2021--2022学年人教版八年级数学下册17.2勾股定理的逆定理课堂训练试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 79.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 18:26:16 | ||
图片预览


文档简介
2022年春人教版初中八年级下册数学课堂提高训练试卷
班级 姓名
第17章 勾股定理
17.2 勾股定理的逆定理
一.选择题(共36分)
1.下列几组数能作为直角三角形的三边长的是( )
A.2,3,4 B.3,4,5 C.12,18,22 D.7,8,9
2.下列选项中不是勾股数的是( )
A.7,24,25 B.4,5,6 C.3,4,5 D.9,12,15
3.关于△ABC,有下列条件:①∠A+∠B=∠C;②∠C=90°;③AC:BC:AB=3:4:5;④a2=(b+c)(b﹣c);⑤∠A:∠B:∠C=2:3:4.其中能确定△ABC是直角三角形的有( )
A.2个 B.3个 C.4个 D.5个
4.已知△ABC的三边长分别是a、b、c,则下列条件中,能判断△ABC是直角三角形的是( )
A.a2=(b+c)(b﹣c) B.a:b:c=12:15:18
C.∠A:∠B:∠C=2:3:4 D.∠A=2∠B=3∠C
5.现有四块正方形纸片,面积分别是2,3,4,5,选取其中三块按如图的方式围成一个三角形,如果要使这个三角形是直角三角形,那么选取的三块纸片的面积分别是( )
A.2,3,4 B.2,3,5 C.2,4,5 D.3,4,5
6.如图长方体木箱的长、宽、高分别为12m,4m,3m,则能放进木箱中的直木棒最长为( )
A.12m B.13m C.15m D.24m
7.有长为5cm,12cm的两根木条,现想找一根木条和这两根木条首尾顺次相连组成直角三角形,则下列木条长度适合的是( )
A.10cm B.13cm C.18cm D.20cm
8.七年级手工小组用彩带给如图所示的图片制作边框,已知AB=5,BC=12,则制作一个边框需要彩带的长度是( )
A.5 B.12 C.13 D.30
9.小明从家出发向正北方向走了150m,接着向正东方向走到离家直线距离为250m远的地方,那么小明向正东方向走的路程是( )
A.250m B.200m C.150m D.100m
10.为了测量学校的景观池的长AB,在BA的延长线上取一点C,使得AC=5米,在点C正上方找一点D(即DC⊥BC),测得∠CDB=60°,∠ADC=30°,则景观池的长AB为( )
A.5米 B.6米 C.8米 D.10米
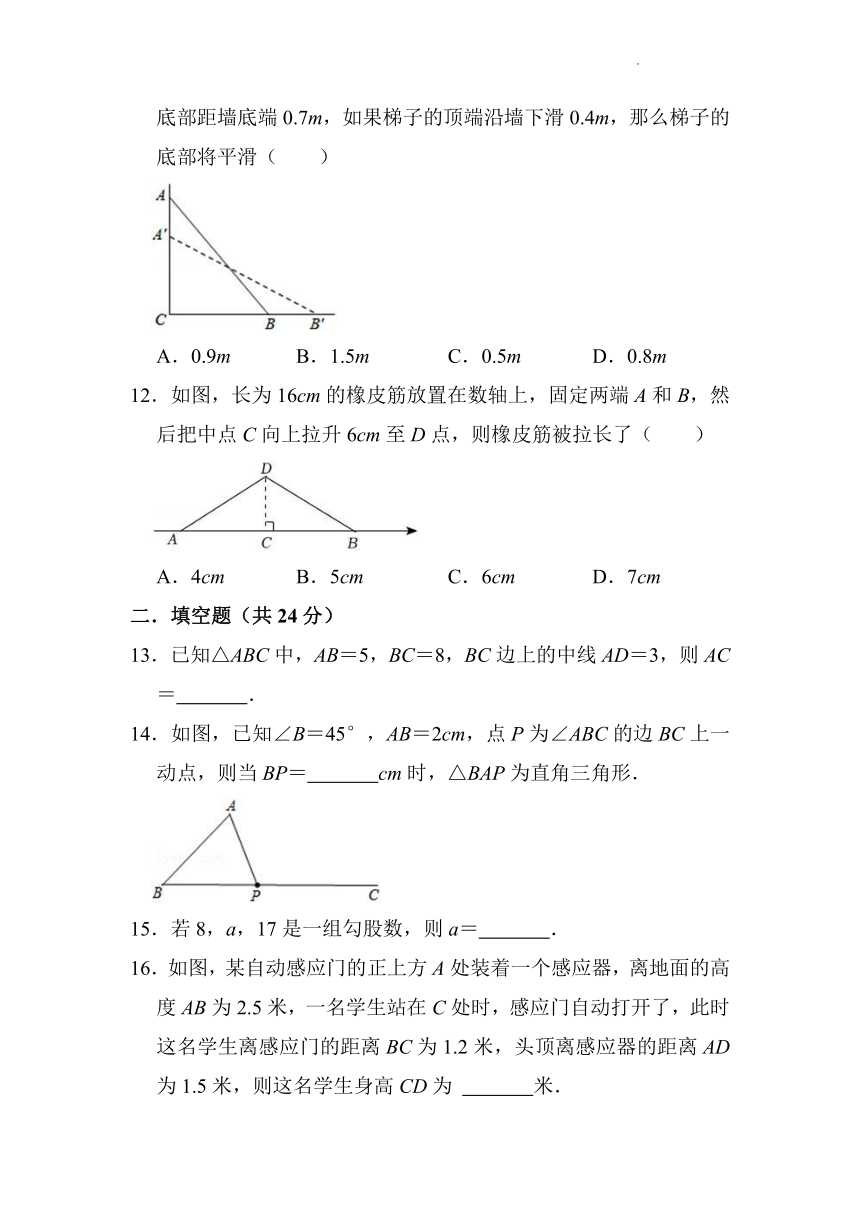
11.如图,一架2.5m长的梯子,斜立在一竖直的墙上,这时梯子的底部距墙底端0.7m,如果梯子的顶端沿墙下滑0.4m,那么梯子的底部将平滑( )
A.0.9m B.1.5m C.0.5m D.0.8m
12.如图,长为16cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C向上拉升6cm至D点,则橡皮筋被拉长了( )
A.4cm B.5cm C.6cm D.7cm
二.填空题(共24分)
13.已知△ABC中,AB=5,BC=8,BC边上的中线AD=3,则AC= .
14.如图,已知∠B=45°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP= cm时,△BAP为直角三角形.
15.若8,a,17是一组勾股数,则a= .
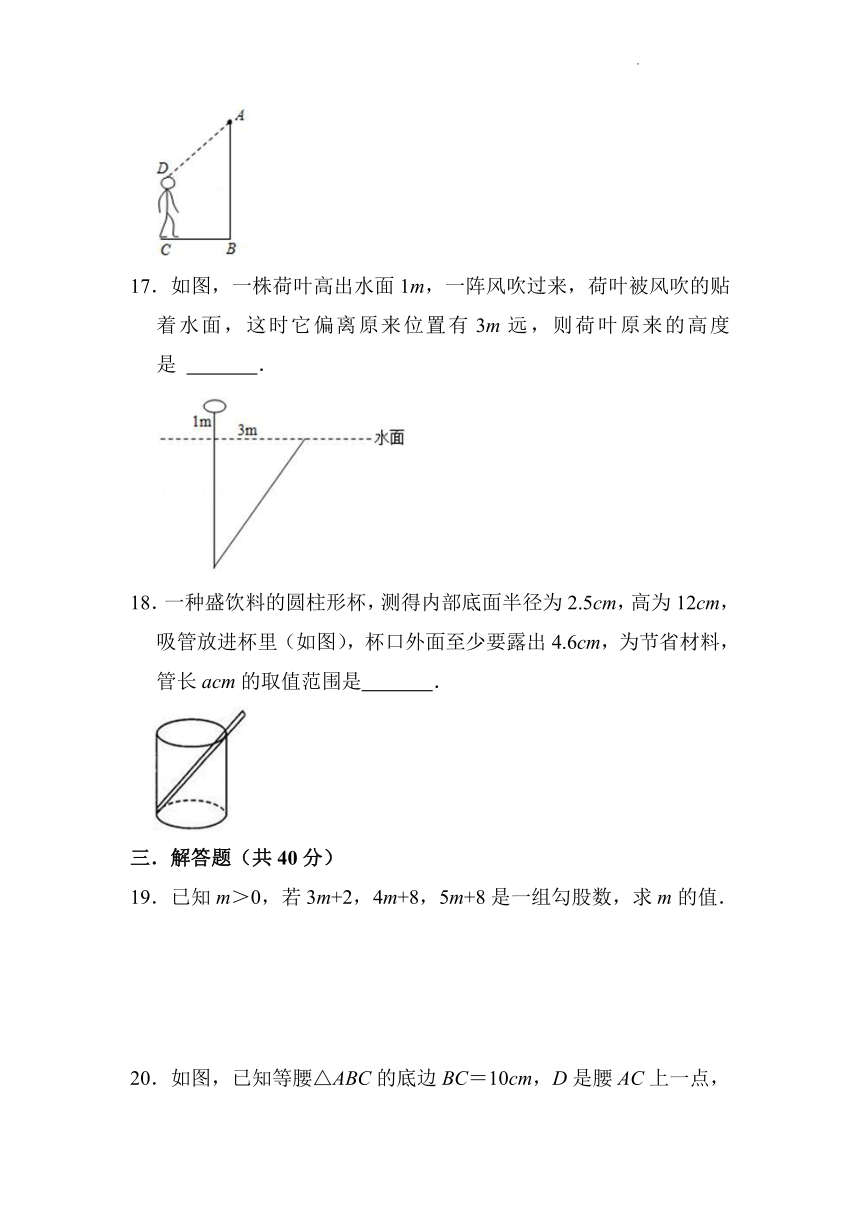
16.如图,某自动感应门的正上方A处装着一个感应器,离地面的高度AB为2.5米,一名学生站在C处时,感应门自动打开了,此时这名学生离感应门的距离BC为1.2米,头顶离感应器的距离AD为1.5米,则这名学生身高CD为 米.
17.如图,一株荷叶高出水面1m,一阵风吹过来,荷叶被风吹的贴着水面,这时它偏离原来位置有3m远,则荷叶原来的高度是 .
18.一种盛饮料的圆柱形杯,测得内部底面半径为2.5cm,高为12cm,吸管放进杯里(如图),杯口外面至少要露出4.6cm,为节省材料,管长acm的取值范围是 .
三.解答题(共40分)
19.已知m>0,若3m+2,4m+8,5m+8是一组勾股数,求m的值.
20.如图,已知等腰△ABC的底边BC=10cm,D是腰AC上一点,且CD=6cm,BD=8cm.
(1)判断△BCD的形状,并说明理由;
(2)求△ABC的周长.
21.如图,在△ABC中,点D是BC边的中点,DE⊥BC交AB于点E,且BE2﹣EA2=AC2.
(1)求证:∠A=90°;
(2)若AC=6,BD=5,求AE的长度.
22.如图,学校操场边上一块空地(阴影部分)需要绿化,连接AC,测出AD=4,AC=5,BC=12,AB=13,AD⊥CD,求需要绿化部分的面积.
23.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:
“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱AB⊥BC,绳索AC比木柱AB长三尺,BC的长度为8尺,求:绳索AC的长度.
参考答案
一.选择题
1.B; 2.B; 3.C; 4.A; 5.B; 6.B; 7.B; 8.D; 9.B; 10.D; 11.D; 12.A;
二.填空题
13.5;
14.或2;
15.15;
16.1.6;
17.5m;
18.16.6≤a≤17.6;
三.解答题
19.
解:由题意得:(3m+2 ) 2+ ( 4m+8) 2= ( 5m+8) 2,
解得: m=1.
20.解:(l) ∵BC= 10cm, CD=8cm, BD=6cm,
∴BC2=BD2+CD2
∴△BDC为直角三角形;
( 2)设AB=x cm,
∵等腰△ABC,
∴AB=AC=x,
∵AC2=AD2+CD2,
即x2= (x-6)2+82,
∴x=
∴OABC的周长=2AB+BC=(cm).
21.
(I)证明:连结CE,
∵D是BC的中点,DE⊥BC,
∴CE= BE,
∵BE2- EA2=Ac2,
∴cE2- EA2=Ac2,
∴EA2+Ac2=cE2,
∴ACE是直角三角形,即∠A=90°;
( 2)解∵D是BC的中点, BD=5,
∴BC= 2BD= 10,
∵∠A=90°, AC=6,
∴AB= = =8
在Rt△AEC中, EA2+Ac2=CE2,
∵CE=BE,
∴62+AE2= (8-AE)2,
解得: AE=
∴AE的长为
22.解:在直角OACD中,AD=4, AC=5,则由勾股定理知: CD= = =3
在△ABC中,AC=5, BC=12, AB= 13,
∵Ac2+Bc2=25+144=169, AB2=132= 169,
∴Ac2+Bc2=AB2,
∴∠ACB=90°,
∴需要绿化部分的面积=S△ABC-S△ACD= 512-34=24,
答:需要绿化部分的面积为24.
23.解:设AC=x尺,则AB= ( x-3)尺,
∵AB⊥BC,
∴△ABC是直角三角形,
由勾股定理得: AB2+Bc2=Ac2,
即(x-3)2+82=x2,
解得: x=12 (尺),
答:绳索AC的长度是12 尺.
班级 姓名
第17章 勾股定理
17.2 勾股定理的逆定理
一.选择题(共36分)
1.下列几组数能作为直角三角形的三边长的是( )
A.2,3,4 B.3,4,5 C.12,18,22 D.7,8,9
2.下列选项中不是勾股数的是( )
A.7,24,25 B.4,5,6 C.3,4,5 D.9,12,15
3.关于△ABC,有下列条件:①∠A+∠B=∠C;②∠C=90°;③AC:BC:AB=3:4:5;④a2=(b+c)(b﹣c);⑤∠A:∠B:∠C=2:3:4.其中能确定△ABC是直角三角形的有( )
A.2个 B.3个 C.4个 D.5个
4.已知△ABC的三边长分别是a、b、c,则下列条件中,能判断△ABC是直角三角形的是( )
A.a2=(b+c)(b﹣c) B.a:b:c=12:15:18
C.∠A:∠B:∠C=2:3:4 D.∠A=2∠B=3∠C
5.现有四块正方形纸片,面积分别是2,3,4,5,选取其中三块按如图的方式围成一个三角形,如果要使这个三角形是直角三角形,那么选取的三块纸片的面积分别是( )
A.2,3,4 B.2,3,5 C.2,4,5 D.3,4,5
6.如图长方体木箱的长、宽、高分别为12m,4m,3m,则能放进木箱中的直木棒最长为( )
A.12m B.13m C.15m D.24m
7.有长为5cm,12cm的两根木条,现想找一根木条和这两根木条首尾顺次相连组成直角三角形,则下列木条长度适合的是( )
A.10cm B.13cm C.18cm D.20cm
8.七年级手工小组用彩带给如图所示的图片制作边框,已知AB=5,BC=12,则制作一个边框需要彩带的长度是( )
A.5 B.12 C.13 D.30
9.小明从家出发向正北方向走了150m,接着向正东方向走到离家直线距离为250m远的地方,那么小明向正东方向走的路程是( )
A.250m B.200m C.150m D.100m
10.为了测量学校的景观池的长AB,在BA的延长线上取一点C,使得AC=5米,在点C正上方找一点D(即DC⊥BC),测得∠CDB=60°,∠ADC=30°,则景观池的长AB为( )
A.5米 B.6米 C.8米 D.10米
11.如图,一架2.5m长的梯子,斜立在一竖直的墙上,这时梯子的底部距墙底端0.7m,如果梯子的顶端沿墙下滑0.4m,那么梯子的底部将平滑( )
A.0.9m B.1.5m C.0.5m D.0.8m
12.如图,长为16cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C向上拉升6cm至D点,则橡皮筋被拉长了( )
A.4cm B.5cm C.6cm D.7cm
二.填空题(共24分)
13.已知△ABC中,AB=5,BC=8,BC边上的中线AD=3,则AC= .
14.如图,已知∠B=45°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP= cm时,△BAP为直角三角形.
15.若8,a,17是一组勾股数,则a= .
16.如图,某自动感应门的正上方A处装着一个感应器,离地面的高度AB为2.5米,一名学生站在C处时,感应门自动打开了,此时这名学生离感应门的距离BC为1.2米,头顶离感应器的距离AD为1.5米,则这名学生身高CD为 米.
17.如图,一株荷叶高出水面1m,一阵风吹过来,荷叶被风吹的贴着水面,这时它偏离原来位置有3m远,则荷叶原来的高度是 .
18.一种盛饮料的圆柱形杯,测得内部底面半径为2.5cm,高为12cm,吸管放进杯里(如图),杯口外面至少要露出4.6cm,为节省材料,管长acm的取值范围是 .
三.解答题(共40分)
19.已知m>0,若3m+2,4m+8,5m+8是一组勾股数,求m的值.
20.如图,已知等腰△ABC的底边BC=10cm,D是腰AC上一点,且CD=6cm,BD=8cm.
(1)判断△BCD的形状,并说明理由;
(2)求△ABC的周长.
21.如图,在△ABC中,点D是BC边的中点,DE⊥BC交AB于点E,且BE2﹣EA2=AC2.
(1)求证:∠A=90°;
(2)若AC=6,BD=5,求AE的长度.
22.如图,学校操场边上一块空地(阴影部分)需要绿化,连接AC,测出AD=4,AC=5,BC=12,AB=13,AD⊥CD,求需要绿化部分的面积.
23.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:
“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱AB⊥BC,绳索AC比木柱AB长三尺,BC的长度为8尺,求:绳索AC的长度.
参考答案
一.选择题
1.B; 2.B; 3.C; 4.A; 5.B; 6.B; 7.B; 8.D; 9.B; 10.D; 11.D; 12.A;
二.填空题
13.5;
14.或2;
15.15;
16.1.6;
17.5m;
18.16.6≤a≤17.6;
三.解答题
19.
解:由题意得:(3m+2 ) 2+ ( 4m+8) 2= ( 5m+8) 2,
解得: m=1.
20.解:(l) ∵BC= 10cm, CD=8cm, BD=6cm,
∴BC2=BD2+CD2
∴△BDC为直角三角形;
( 2)设AB=x cm,
∵等腰△ABC,
∴AB=AC=x,
∵AC2=AD2+CD2,
即x2= (x-6)2+82,
∴x=
∴OABC的周长=2AB+BC=(cm).
21.
(I)证明:连结CE,
∵D是BC的中点,DE⊥BC,
∴CE= BE,
∵BE2- EA2=Ac2,
∴cE2- EA2=Ac2,
∴EA2+Ac2=cE2,
∴ACE是直角三角形,即∠A=90°;
( 2)解∵D是BC的中点, BD=5,
∴BC= 2BD= 10,
∵∠A=90°, AC=6,
∴AB= = =8
在Rt△AEC中, EA2+Ac2=CE2,
∵CE=BE,
∴62+AE2= (8-AE)2,
解得: AE=
∴AE的长为
22.解:在直角OACD中,AD=4, AC=5,则由勾股定理知: CD= = =3
在△ABC中,AC=5, BC=12, AB= 13,
∵Ac2+Bc2=25+144=169, AB2=132= 169,
∴Ac2+Bc2=AB2,
∴∠ACB=90°,
∴需要绿化部分的面积=S△ABC-S△ACD= 512-34=24,
答:需要绿化部分的面积为24.
23.解:设AC=x尺,则AB= ( x-3)尺,
∵AB⊥BC,
∴△ABC是直角三角形,
由勾股定理得: AB2+Bc2=Ac2,
即(x-3)2+82=x2,
解得: x=12 (尺),
答:绳索AC的长度是12 尺.
