浙科版生物必修3第二节《 种群的增长方式》课件4
文档属性
| 名称 | 浙科版生物必修3第二节《 种群的增长方式》课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 543.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙科版 | ||
| 科目 | 生物学 | ||
| 更新时间 | 2012-12-24 00:00:00 | ||
图片预览





文档简介
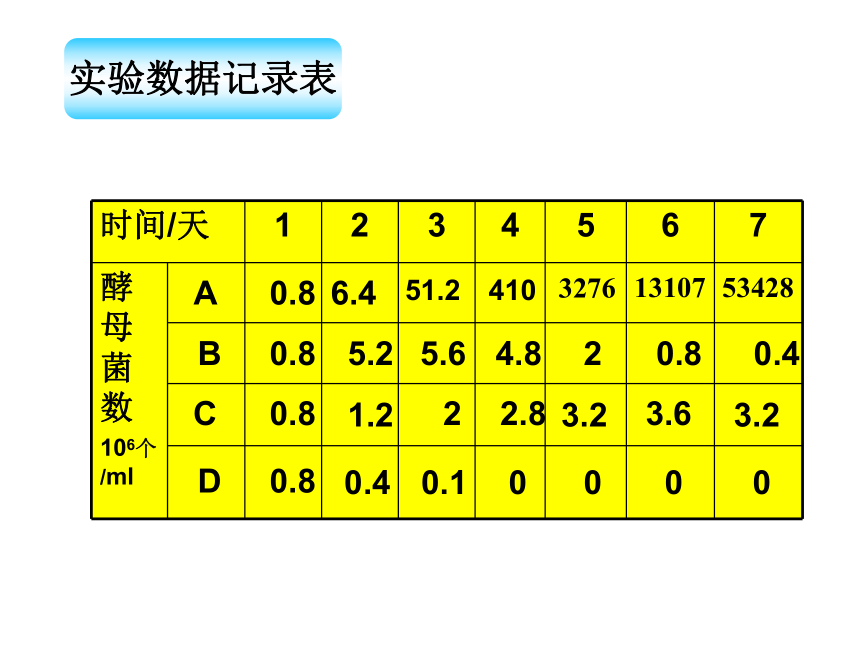
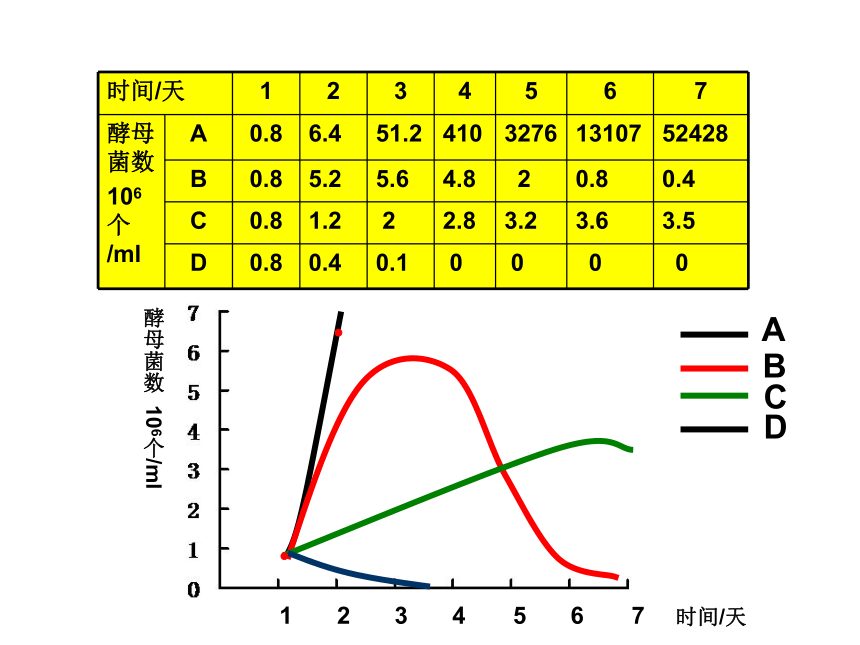
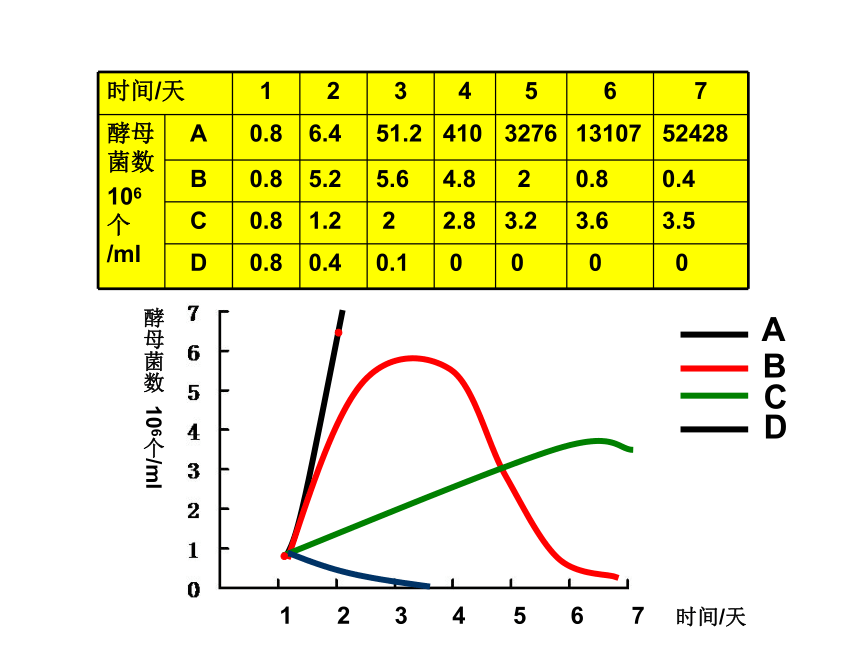
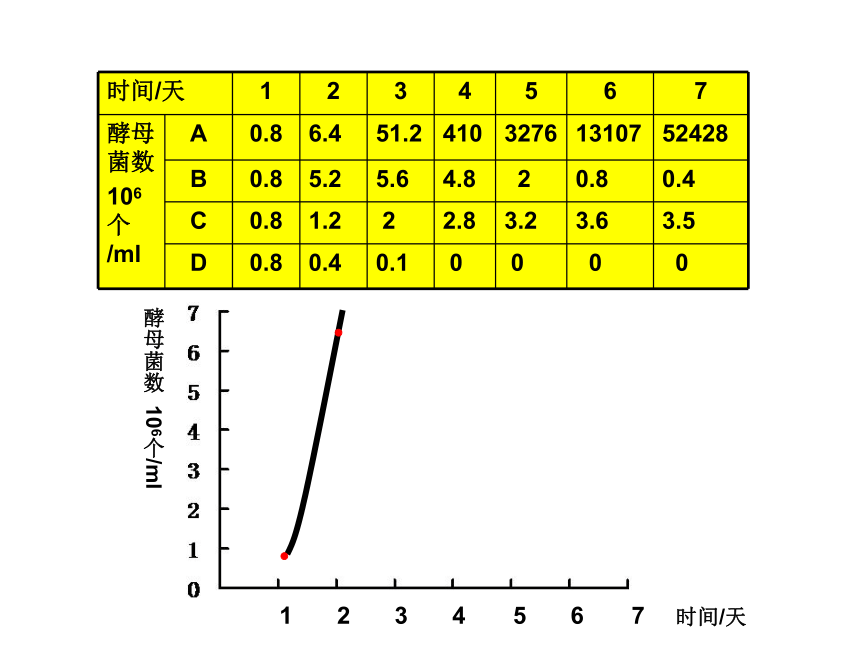
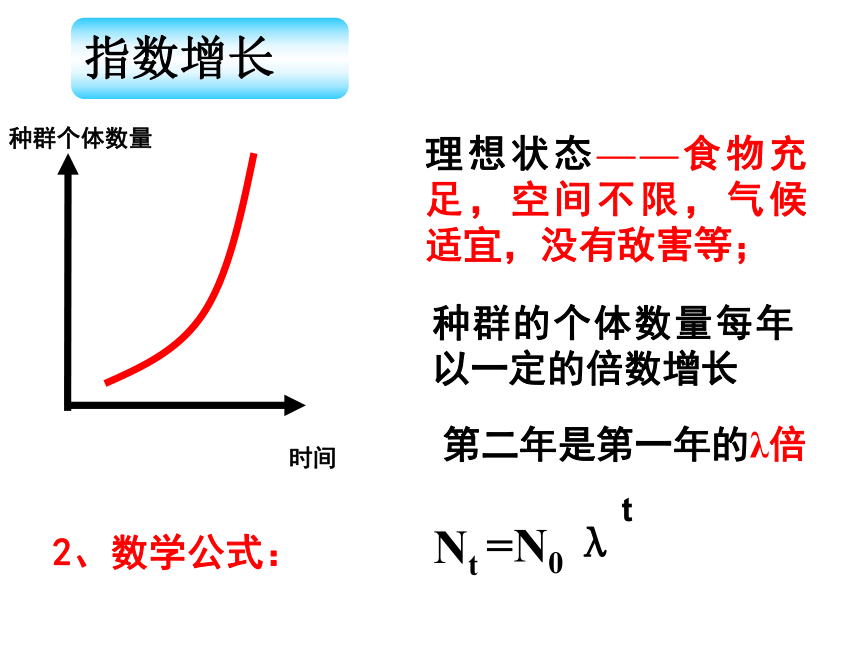
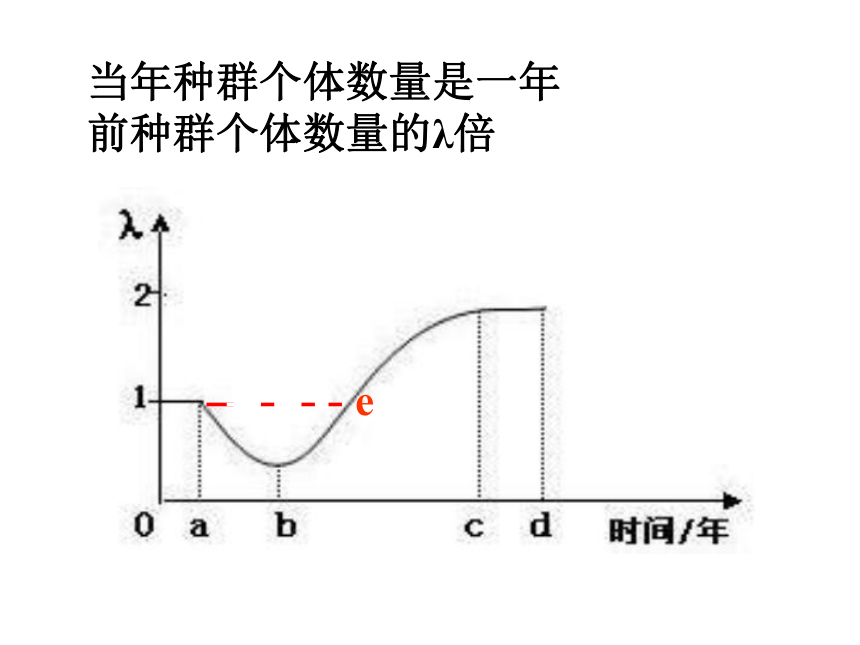
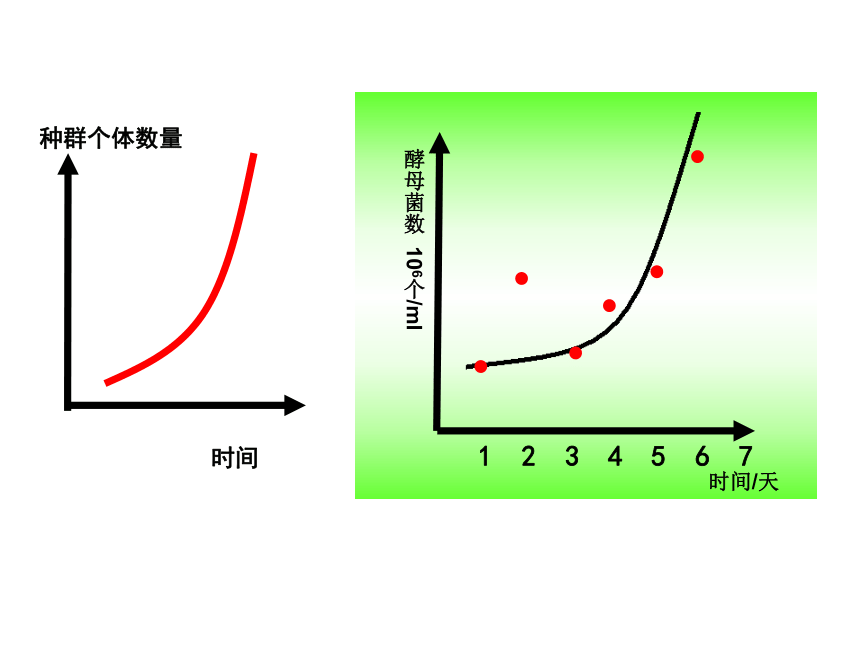
课件43张PPT。种群的增长方式孙 艳舟 山 中 学实验数据记录表0.8 0.8 1.2 0.4 2 2.8 3.2 3.6 3.2 0.1 0 0 0 0 C D 1234567时间/天酵母菌数 106个/ml1234567时间/天酵母菌数 106个/ml1234567时间/天酵母菌数 106个/ml理想状态——食物充足,空间不限,气候适宜,没有敌害等;种群的个体数量每年以一定的倍数增长2、数学公式:Nt=N0 λt指数增长第二年是第一年的λ倍当年种群个体数量是一年前种群个体数量的λ倍1234567时间/天酵母菌数 106个/ml1234567时间/天酵母菌数 106个/ml1234567时间/天酵母菌数 106个/mlBCAD资源空间有限K环境容纳量
( K值)逻辑斯谛增长 食物有限空间有限K/2(现有个体数-原有个体数)/增长时间 种群在单位时间内净增加的个体数占个体总数的比率 指单位时间种群增长数量 (现有个体数-原有个体数)/原有个体数 时间时间K/2时间时间Nt-Nt-1Nt-1N0 λt -N0 λt-1 N0 λt-1 时间时间λ-1时间λ-1时间λ-1时间λ-1时间λ-1时间λ-1时间λ-1例:如图为两种生物种群的生长曲线,以下说法错误的是
A.按甲曲线增长的种群无K值,无种内斗争,增长率始终不变。
B.按乙曲线增长的种群,到a点后种内斗争最为激烈,且增长率为零。
C.按乙曲线类型增长的不同种群,在同一环境下,b点时的增长速率不同,但均为最大值。
D.甲曲线的数学模型为 ,其中λ代表增长率
Nt=N0 λtD时间数学模型:
概念:用来描述一个系统变化的数学形式。
类型:
(1)数据分析表格式
(2)坐标式
(曲线图、柱状图)(3)数学方程式
图4-4 细菌每20min分裂一次时的指数增长曲线(“J” 形曲线)t图4-4 细菌每20min分裂一次时的指数增长曲线(“J” 形曲线)教材中的数学模型光饱和点 光强度
图3--24 光强度对光合速率的影响光合速率教材中的数学模型10-8 10-6 10-4 10-2 1 102生长素浓度(g/L)促进生长
抑制生长教材中的数学模型图1-5 生长素浓度对根和茎细胞生长的影响将具体内容转换成数学模型例:果蝇(2N=8)它的一个次级精母细胞中的染色体数为4或8利用数学模型来分析具体的问题把一个外来物种种群引入到一个新环境中可能会出现怎样的情况石榴
葡萄
樱桃
番茄
甘蓝
马铃薯悬铃木茉莉花
……利用数学模型来分析具体的问题把一个外来物种种群引入到一个新环境中可能会出现怎样的情况注意数学模型中的条件的变化课堂小结指数增长逻辑斯谛增长 数学模型(10浙江卷)某生态系统中生活着多种植食性动物,其中某一植食性动物种群个体数量的变化如图所示。若不考虑该系统内生物个体的迁入与迁出,下列关于该种群个体数量变化的叙述,错误的是( )
若a点时环境因素发生变化,但食物量不变,则a点以后个体数量变化不符合逻辑斯谛增长
若该种群出生率提高,个体数量的增加也不会大幅走过b点
天敌的大量捕食会导致该种群个体数量下降,下降趋势与b-c段相似
年龄结构变动会导致该种群个体数量发生波动,波动趋势与c-d段相似实战演练
( K值)逻辑斯谛增长 食物有限空间有限K/2(现有个体数-原有个体数)/增长时间 种群在单位时间内净增加的个体数占个体总数的比率 指单位时间种群增长数量 (现有个体数-原有个体数)/原有个体数 时间时间K/2时间时间Nt-Nt-1Nt-1N0 λt -N0 λt-1 N0 λt-1 时间时间λ-1时间λ-1时间λ-1时间λ-1时间λ-1时间λ-1时间λ-1例:如图为两种生物种群的生长曲线,以下说法错误的是
A.按甲曲线增长的种群无K值,无种内斗争,增长率始终不变。
B.按乙曲线增长的种群,到a点后种内斗争最为激烈,且增长率为零。
C.按乙曲线类型增长的不同种群,在同一环境下,b点时的增长速率不同,但均为最大值。
D.甲曲线的数学模型为 ,其中λ代表增长率
Nt=N0 λtD时间数学模型:
概念:用来描述一个系统变化的数学形式。
类型:
(1)数据分析表格式
(2)坐标式
(曲线图、柱状图)(3)数学方程式
图4-4 细菌每20min分裂一次时的指数增长曲线(“J” 形曲线)t图4-4 细菌每20min分裂一次时的指数增长曲线(“J” 形曲线)教材中的数学模型光饱和点 光强度
图3--24 光强度对光合速率的影响光合速率教材中的数学模型10-8 10-6 10-4 10-2 1 102生长素浓度(g/L)促进生长
抑制生长教材中的数学模型图1-5 生长素浓度对根和茎细胞生长的影响将具体内容转换成数学模型例:果蝇(2N=8)它的一个次级精母细胞中的染色体数为4或8利用数学模型来分析具体的问题把一个外来物种种群引入到一个新环境中可能会出现怎样的情况石榴
葡萄
樱桃
番茄
甘蓝
马铃薯悬铃木茉莉花
……利用数学模型来分析具体的问题把一个外来物种种群引入到一个新环境中可能会出现怎样的情况注意数学模型中的条件的变化课堂小结指数增长逻辑斯谛增长 数学模型(10浙江卷)某生态系统中生活着多种植食性动物,其中某一植食性动物种群个体数量的变化如图所示。若不考虑该系统内生物个体的迁入与迁出,下列关于该种群个体数量变化的叙述,错误的是( )
若a点时环境因素发生变化,但食物量不变,则a点以后个体数量变化不符合逻辑斯谛增长
若该种群出生率提高,个体数量的增加也不会大幅走过b点
天敌的大量捕食会导致该种群个体数量下降,下降趋势与b-c段相似
年龄结构变动会导致该种群个体数量发生波动,波动趋势与c-d段相似实战演练
同课章节目录
- 第一章 植物生命活动的调节
- 第一节 植物激素调节
- 第二节 其他调节
- 第二章 动物生命活动的调节
- 第一节 内环境与稳态
- 第二节 神经系统的结构与功能
- 第三节 高等动物的内分泌系统与体液调节
- 第三章 免疫系统与免疫功能
- 第一节 人体对抗病原体感染的非特异性防卫
- 第二节 特异性反应(免疫应答)
- 第三节 免疫系统的功能异常
- 第四章 种群
- 第一节 种群的特征
- 第二节 种群的增长方式
- 第三节 种群的数量波动及调节
- 第五章 群落
- 第一节 群落的物种组成和优势种
- 第二节 植物的生长型和群落结构
- 第三节 物种在群落中的生态位
- 第四节 群落的主要类型
- 第五节 群落演替
- 第六章 生态系统
- 第一节 生态系统的营养结构
- 第二节 生态系统中的生产量和生物量
- 第三节 能量流动和物质循环
- 第四节 生态系统的稳态及其调节
- 第七章 人类与环境
- 第一节 生物圈
- 第二节 全球人口动态
- 第三节 人类对全球环境的影响
