第九章 概率初步 单元测试题（含答案）

中小学教育资源及组卷应用平台
《第九章 概率初步》单元测试题
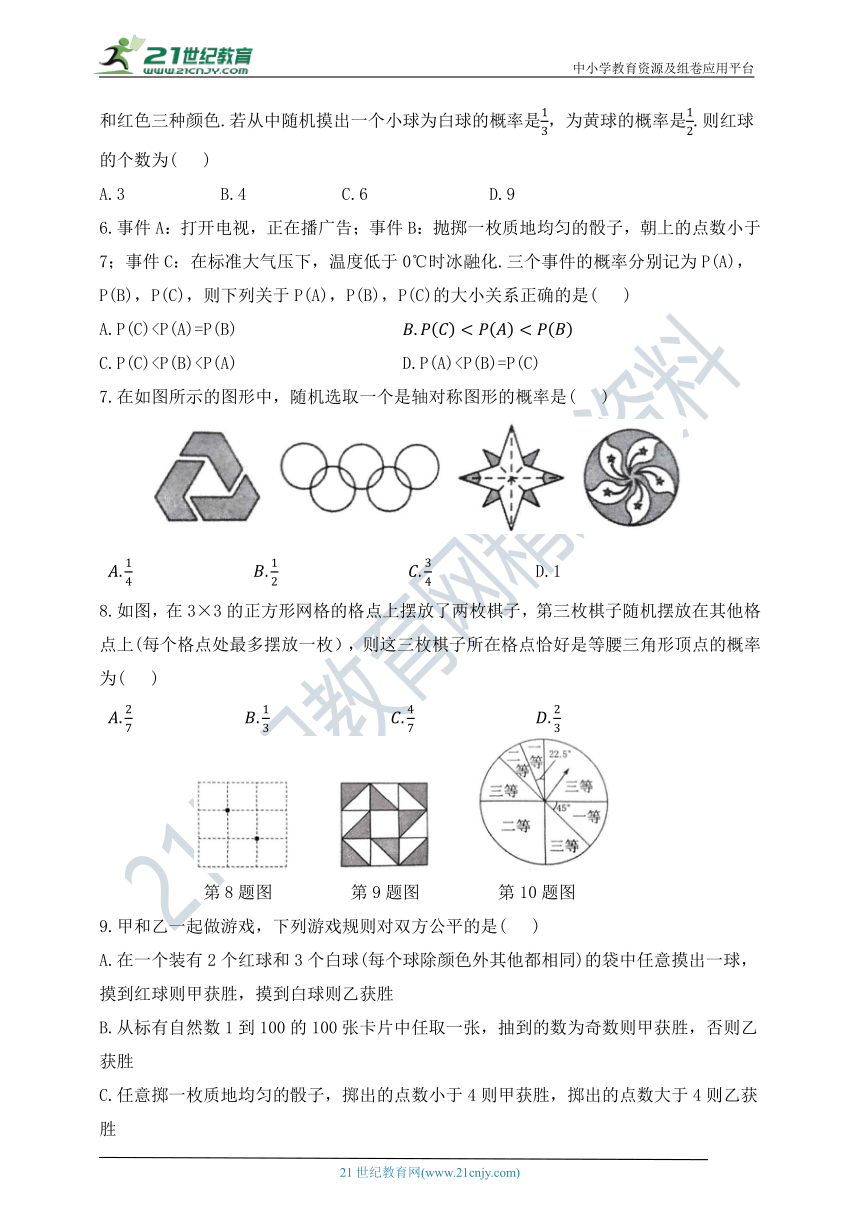
(满分：100分 时间：60分钟)
一、选择题(每小题3分，共30分)
1.若“一个不透明的袋中装有三个球,分别标有1,2,x这三个号码,这些球除号码外都相同,搅匀后任意摸出一个球,摸出球上的号码小于5”是必然事件,则x的值可能是( )
A.4 B.5 C.6 D.7
2.下列说法正确的是( )
A.某种彩票中奖的概率是1%，则买1000张彩票一定有10张中奖
B.任意掷一枚质地均匀的骰子，掷出的点数是奇数的概率是
C.天气预报说明天的降水概率为90%，则明天一定会下雨
D. 367人中至少有2人生日相同
3.如图是一些可以自由转动的转盘，按照转出黄色的可能性由大到小进行排列正确的是 ( )
A. ②④①③ B. ①②③④ C. ③①④② D. ④①③②
4.如图①，平整的地面上有一个不规则图案(涂色部分)，小明想了解该图案的面积是多少，他采取了以下办法：用一个长为5m，宽为4m的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计试验结果），他将若干次有效试验的结果绘制成了如图②所示的折线统计图，由此他估计不规则图案的面积为（ ）
5.在一个不透明的盒子中装有18个除颜色不同外，其余均相同的小球，共有白色、黄色和红色三种颜色.若从中随机摸出一个小球为白球的概率是，为黄球的概率是.则红球的个数为( )
A.3 B.4 C.6 D.9
6.事件A：打开电视，正在播广告；事件B：抛掷一枚质地均匀的骰子，朝上的点数小于7；事件C：在标准大气压下，温度低于0℃时冰融化.三个事件的概率分别记为P(A)，P(B)，P(C)，则下列关于P(A)，P(B)，P(C)的大小关系正确的是( )
A.P(C)C.P(C)7.在如图所示的图形中，随机选取一个是轴对称图形的概率是( )
D.1
8.如图，在3×3的正方形网格的格点上摆放了两枚棋子，第三枚棋子随机摆放在其他格点上(每个格点处最多摆放一枚），则这三枚棋子所在格点恰好是等腰三角形顶点的概率为( )
第8题图 第9题图 第10题图
9.甲和乙一起做游戏，下列游戏规则对双方公平的是( )
A.在一个装有2个红球和3个白球(每个球除颜色外其他都相同)的袋中任意摸出一球，摸到红球则甲获胜，摸到白球则乙获胜
B.从标有自然数1到100的100张卡片中任取一张，抽到的数为奇数则甲获胜，否则乙获胜
C.任意掷一枚质地均匀的骰子，掷出的点数小于4则甲获胜，掷出的点数大于4则乙获胜
D.让小球在如图所示的地板上自由滚动，并随机地停在某块方块上，小球停在涂色区域则甲获胜，停在白色区域则乙获胜
10.为了吸引顾客，某餐饮店推出转盘抽奖打折活动.如图是可以自由转动的转盘，转盘被分成若干个扇形.转动转盘，转盘停止后，指针所指区域内的等级可作为打折等级（指针指向分界线则重转）.其中，一等打九折，二等打九五折，三等赠送小礼品.小明和同学周六去聚餐，他们转动一次转盘能够得到九折优惠的概率是( )
二、填空题(每小题3分，共18分)
11.小东认为任意抛掷一个啤酒瓶盖，啤酒瓶盖落地后印有商标一面向上的可能性的大小是，你认为小东的想法_________（填“合理＂或“不合理”），理由是＿＿＿＿＿___
_______________________________________________.
12.某校七年级开展“读书月”活动，并将授予该月阅读课外书籍4册以上(含4册)的学生“阅读之星”的称号.七年级少先队大队委进行了随机调查，结果如下表所示：
阅读册数 O 1 2 3 4 5
学生人数 20 18 27 70 12 3
可以估计该年级学生获得此称号的概率是＿______＿.
13.在-2.-1，1，2这四个数中随机取出一个数，其倒数等于本身的概率是_________.
14.如图是一个正方形靶子，从里到外三个正方形的边长之比为1：2：3，则打中涂色区域的概率为＿＿＿.
15.动物学家通过大量的调查，估计某种动物活到20岁的概率为0.8，活到25岁的概率为0.5.据此若设刚出生的这种动物共有a只，则20年后存活的有____________只，现年20岁的这种动物活到25岁的概率为______________.
16.超市要举行转盘摇奖活动，转盘如图所示，买满200元摇奖一次.其中各个带阴影的小扇形的圆心角的度数均为15%，各个空白扇形的圆心角度数均相等.若某位顾客买满200元，则他中奖的概率为_________，获得自行车的概率为＿＿_＿＿.
三、解答题(共52分)
17.(8分)下列成语中，哪些刻画的是必然事件 哪些刻画的是不可能事件 哪些刻画的是随机事件
(1)万无一失；(2)胜败乃兵家常事；(3)十拿九稳；(4)海枯石烂；(5)百战百胜；(6)九死一生.
18.(12分)在“世界读书日”来临之际，某校开展了“我因阅读而成长”的赠书活动.如图，设置了一个可以自由转动的转盘，并规定：每名学生可获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得一本相应的书籍.下表是活动中的一组统计数据.
转动转盘的次数n 100 200 400 500 1000
落在《红星照耀中国》区域的次数m 44 92 182 225 450
落在《红星照耀中国》区域的频率(精确到0.001) 0.440 0.460 0.455 0.450 0.450
(1)自由转动转盘，计算转盘停止后，指针落在《海底两万里》区域的概率；
(2)根据上表，如果转动转盘1500次，那么指针落在《红星照耀中国》区域大约有多少次
19.(10分)某公司的一批某品牌衬衣的质量抽检结果如下表：
捕枪件数 50 100 200 300 400 500
次品件数 4 16 19 24 36
(1)请结合表格中的数据直接写出从这批衬衣中任意抽1件是次品的概率；
(2)如果销售这批衬衣600件，那么至少要准备多少件正品衬衣供买到次品的顾客退换
20.(10分)如图①②均是一个均匀的可以自由转动的转盘，图①被分成9等份，分别标有1，2，3，4，5，6，7，8，9这9个数字.转动转盘，当转盘停止后，指针指向的数字即为转出的数字(当指针恰好指在分界线上时重转）；图②被涂上红色与绿色，转动转盘，当转盘停止后，指针指向的颜色即为转出的颜色（当指针恰好指在分界线上时重转）.小明转动图①的转盘，小亮转动图②的转盘.
(1)求小明转出的数字小于7的概率.
(2)小颖认为，小明转出来的数字小于7的概率与小亮转出的颜色是红色的概率相同，她的看法对吗 请说明理由.
21.(12分)小军与小玲共同发明了一种“字母棋”，进行比胜负的游戏。他们用四个字母做成10枚棋子，如图，棋子A有1枚，棋子B有2枚，棋子C有3枚，棋子D有4枚.“字母棋”的游戏规则如下：①游戏时两人各摸一枚棋子进行比赛称为一轮比赛，先摸者摸出的棋子不放回；②棋子A胜棋子B、棋子C，棋子B胜棋子C、棋子D，棋子C胜棋子D，棋子D胜棋子A；③相同棋子不分胜负.
(1)若小玲先摸，则小玲摸到棋子C的概率是多少
(2)已知小玲先摸到了棋子C，小军在剩余的9枚棋子中随机摸一枚，这一轮小玲胜小军的概率是多少
(3)当小玲摸到什么棋子时，胜小军的概率最大
参考答案
一、1.A 2.D 3.C 4.B 5.A 6.B 7.B 8.C 9.B 10.C
二、11.不合理 啤酒瓶盖的正反两面不均匀，抛掷后向上一面的两种可能性不相等 13. 15.0.8a 16.
三、17.(1)(5)刻画的是必然事件 (4)刻画的是不可能事件 (2)(3)(6)刻画的是随机事件
18.(1)指针落在《海底两万里》区域的概率为
(2)由表格中数据的变化趋势可知，随着转动转盘次数的增加，指针落在《红星照耀中国》区域的频率稳定在0.45附近，∴指针落在《红星照耀中国》区域的概率约为0.45.∴转动转盘1500次，指针落在《红星照耀中国》区域大约有1500×0.45=675(次).
19.(1)从这批衬衣中任意抽1件是次品的概率约为0.06；
(2)600×0. 06=36(件)，∴至少要准备36件正品衬衣供买到次品的顾客退换.
20.(1)∵题图①的转盘被分成9等份，转到每个数字的可能性相等，共有9种可能的结果，数字小于7的结果有6种，∴转出来的数字小于7的概率是
(2)她的看法对 理由：∵题图②的转盘被涂上红色与绿色，其中绿色部分）所在扇形圆心角的度数是120°，∴红色部分所在扇形圆心角的度数是360°―120°=240°，转出的颜色是红色的概率是 ∴小明转出来的数字小于7的概率与小亮转出的，颜色是红色的概率相同.∴小颖的看法对.
21.(1)小玲摸到棋子C的概率是
(2)只有小军摸到棋子D，小玲才能获胜，故小玲胜小军的概率是
(3)若小玲摸到棋子A，则小玲胜小军的概率是；若小玲摸到棋子B，则小玲胜小军的概率是：若小玲摸到棋子C，则小玲胜小军的概率是；若小玲摸到棋子D，则小玲胜小军的概率是 . ∵ ∴当小玲摸到棋子B时，胜小军的概率最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)