8.2 消元——解二元一次方程组(第2课时) 课件(共44张PPT)
文档属性
| 名称 | 8.2 消元——解二元一次方程组(第2课时) 课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 21:39:16 | ||
图片预览











文档简介
(共44张PPT)
人教版 · 数学· 七年级(下)
第八章 二元一次方程组
8.2 消元——解二元一次方程组
第2课时 用加减法解二元一次方程组
1.掌握用加减消元法解二元一次方程组的步骤.
2.熟练运用消元法解简单的二元一次方程组.
3.培养分析能力,能迅速根据所给的二元一次方程组,选择一种简单的方法解方程组.
学习目标
一个长方形的周长是50cm,长比宽多5cm,设长为xcm,
宽为ycm,可列出的二元一次方程组是
x – y = 5 ①
2x+ 2y = 50 ②
上面方程组的两个方程中,y的系数有什么关系?
利用这种关系你能发现新的消元方法吗?
导入新知
怎样解下面的二元一次方程组呢?
①
②
新知一 加减法解二元一次方程组
合作探究
把②变形得:
代入①,不就消去x了!
小彬
把②变形得
可以直接代入①呀!
小明
(3x+5y)+(2x-5y)= 21 + (-11)
3x+5y = 21
2x-5y = -11
和
互为相反数……
按小丽的思路,你能消去
一个未知数吗?
小丽
分析:
,①
. ②
①左边 + ②左边 = ①右边 + ②右边
把x=2代入①,得y=3,
的解是
所以
x=2
3x+5y+2x-5y=10
5x+0y=10
5x=10
2x-5y=7,①
2x+3y=-1. ②
参考小丽的思路,怎样解下面的二元一次方程组呢?
分析:观察方程组中的两个方程,未知数x的系数相等,即都是2.所以把这两个方程两边分别相减,就可以消去未知数x,得到一个一元一次方程.
解:由 ②-①得:8y=-8,
y=-1 .
把y =-1代入①,得
2x-5×(-1)=7,
解得:x=1 .
所以原方程组的解是
上面这些方程组的特点是什么?
解这类方程组的基本思路是什么?主要步骤有哪些?
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元.
加减消元:
消去一个元;
分别求出两个未知数的值;
写出原方程组的解.
同一个未知数的系数相同或互为相反数.
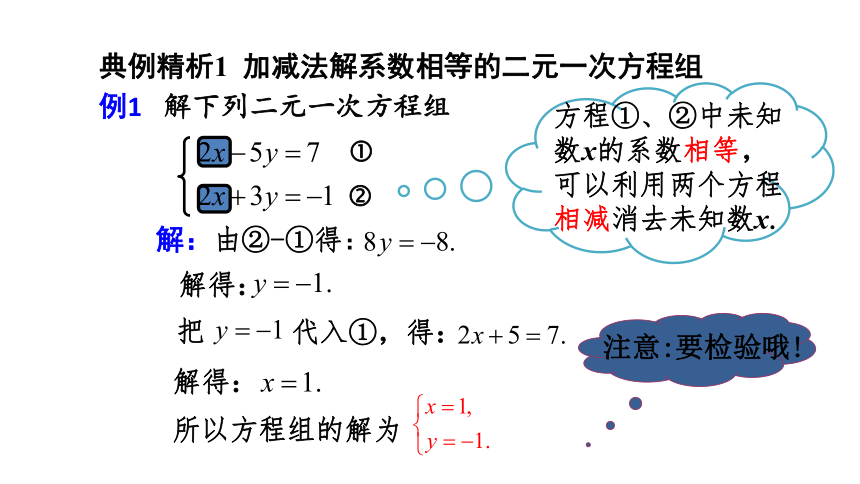
例1 解下列二元一次方程组
解:由②-①得:
解得:
把
代入①,得:
注意:要检验哦!
解得:
所以方程组的解为
方程①、②中未知数x的系数相等,可以利用两个方程相减消去未知数x.
典例精析1 加减法解系数相等的二元一次方程组
①
②
3x+2y=23
5x+2y=33
解方程组
解:
由②-①得:
将x=5代入①得:
15+2y=23,
y=4.
所以原方程组的解是
x=5,
y=4.
2x=10,
x=5.
与前面的代入法相比,是不是更加简单了!
巩固新知
3x +10 y=2.8 ①
15x -10 y=8 ②
解:把 ①+②得: 18x=10.8, x=0.6.
把x=0.6代入①,得:
3×0.6+10y=2.8,
解得:y=0.1.
例2 解方程组
所以这个方程组的解是
x=0.6,
y=0.1.
典例精析2 加减法解系数为相反数的二元一次方程组
互为相反数
相加
同一未知数的
系数 _
时,把两个方程
的两边分别 !
合作探究
①
②
解:由①+②得:
把x=2代入①,得:
y=3.
x=2.
所以原方程组的解是
5x=10,
解二元一次方程组:
巩固新知
像上面这种解二元一次方程组的方法,叫做加减消元法,简称加减法.
当方程组中两个方程的某个未知数的系数互为相反数或相等时,可以把方程的两边分别相加(系数互为相反数)或相减(系数相等)来消去这个未知数,得到一个一元一次方程,进而求得二元一次方程组的解.
合作探究
例3 用加减法解方程组:
①
②
解: ①×2得:
4x - 6y =8. ③
③ + ②得:
7x =14,
x =2.
把x =1代入①,得:
y =0.
∴原方程组的解是
x =2,
y =0.
{
典例精析3 加减法解找系数最小公倍数的二元一次方程组
同一未知数的系数 时,利用等
式的性质,使得未知数的系数 .
不相等也不互为相反数
相等或互为相反数
找系数的最小公倍数
1.用加减法解方程组:
①
②
①×3得:
所以原方程组的解是
解:
③-④得: y=2.
把y=2代入①,
解得: x=3.
②×2得:
6x+9y=36. ③
6x+8y=34. ④
巩固新知
解: ②×4得:
所以原方程组的解为
①
2.解方程组:
②
③
①+③得:7x = 35,
解得:x = 5.
把x = 5代入②得,y = 1.
4x-4y=16.
2台大收割机和5台小收割机均工作2h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
分析:题目中存在的两个等量关系:
2×(2台大收割量+5台小收割量)=______
5×(3台大收割量+2台小收割量)=______
3.6hm2
8hm2
新知二 列二元一次方程组解实际问题
合作探究
3.6
整理,得
解:设一台大收割机和一台小收割机每小时各收割小麦x hm2和y hm2.根据题意,得
②-①,得 __________
解得 x=_______
把x=_____ 代入①,得y=_______
∴这个方程组的解为
答:一台大收割机和一台小收割机每小时分别收割小麦0.4hm2和0.2hm2
4x+10y
15x+10y
8
11x=4.4
0.4
0.4
0.2
0.2
0.4
3.6
3x+2y
8
2x+5y
①
②
利用二元一次方程组解决实际问题的基本步骤是:
(1)依题意,找________关系;
(2)根据等量关系设_______;
(3)列__________;
(4)解__________;
(5)检验并作答.
等量关系
未知数
方程组
方程组
归纳小结
一条船顺流航行,每小时行20km,逆流航行,每小时行16km,求轮船在静水中的速度与水的速度.
解:设轮船在静水中的速度为xkm/h,水流的速度为ykm/h
由题意得:
解得
答:轮船在静水中的速度为18km/h,水流的速度为2km/h.
巩固新知
A
课堂练习
D
加
减
D
B
①×3-②×2
①×2+②×3
9.(8分)(海南中考)时下正是海南百香果丰收的季节,张阿姨到“海南爱心扶贫网”上选购百香果,若购买2千克“红土”百香果和1千克“黄金”百香果需付80元,若购买1千克“红土”百香果和3千克“黄金”百香果需付115元.请问这两种百香果每千克各是多少元?
加减消元法解二元一次方程组
基本思路“消元”
加减消元法解二元一次方程组的一般步骤
列二元一次方程组解实际问题
归纳新知
A
课后练习
B
1
60
7.(娄底中考)假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
再见
人教版 · 数学· 七年级(下)
第八章 二元一次方程组
8.2 消元——解二元一次方程组
第2课时 用加减法解二元一次方程组
1.掌握用加减消元法解二元一次方程组的步骤.
2.熟练运用消元法解简单的二元一次方程组.
3.培养分析能力,能迅速根据所给的二元一次方程组,选择一种简单的方法解方程组.
学习目标
一个长方形的周长是50cm,长比宽多5cm,设长为xcm,
宽为ycm,可列出的二元一次方程组是
x – y = 5 ①
2x+ 2y = 50 ②
上面方程组的两个方程中,y的系数有什么关系?
利用这种关系你能发现新的消元方法吗?
导入新知
怎样解下面的二元一次方程组呢?
①
②
新知一 加减法解二元一次方程组
合作探究
把②变形得:
代入①,不就消去x了!
小彬
把②变形得
可以直接代入①呀!
小明
(3x+5y)+(2x-5y)= 21 + (-11)
3x+5y = 21
2x-5y = -11
和
互为相反数……
按小丽的思路,你能消去
一个未知数吗?
小丽
分析:
,①
. ②
①左边 + ②左边 = ①右边 + ②右边
把x=2代入①,得y=3,
的解是
所以
x=2
3x+5y+2x-5y=10
5x+0y=10
5x=10
2x-5y=7,①
2x+3y=-1. ②
参考小丽的思路,怎样解下面的二元一次方程组呢?
分析:观察方程组中的两个方程,未知数x的系数相等,即都是2.所以把这两个方程两边分别相减,就可以消去未知数x,得到一个一元一次方程.
解:由 ②-①得:8y=-8,
y=-1 .
把y =-1代入①,得
2x-5×(-1)=7,
解得:x=1 .
所以原方程组的解是
上面这些方程组的特点是什么?
解这类方程组的基本思路是什么?主要步骤有哪些?
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元.
加减消元:
消去一个元;
分别求出两个未知数的值;
写出原方程组的解.
同一个未知数的系数相同或互为相反数.
例1 解下列二元一次方程组
解:由②-①得:
解得:
把
代入①,得:
注意:要检验哦!
解得:
所以方程组的解为
方程①、②中未知数x的系数相等,可以利用两个方程相减消去未知数x.
典例精析1 加减法解系数相等的二元一次方程组
①
②
3x+2y=23
5x+2y=33
解方程组
解:
由②-①得:
将x=5代入①得:
15+2y=23,
y=4.
所以原方程组的解是
x=5,
y=4.
2x=10,
x=5.
与前面的代入法相比,是不是更加简单了!
巩固新知
3x +10 y=2.8 ①
15x -10 y=8 ②
解:把 ①+②得: 18x=10.8, x=0.6.
把x=0.6代入①,得:
3×0.6+10y=2.8,
解得:y=0.1.
例2 解方程组
所以这个方程组的解是
x=0.6,
y=0.1.
典例精析2 加减法解系数为相反数的二元一次方程组
互为相反数
相加
同一未知数的
系数 _
时,把两个方程
的两边分别 !
合作探究
①
②
解:由①+②得:
把x=2代入①,得:
y=3.
x=2.
所以原方程组的解是
5x=10,
解二元一次方程组:
巩固新知
像上面这种解二元一次方程组的方法,叫做加减消元法,简称加减法.
当方程组中两个方程的某个未知数的系数互为相反数或相等时,可以把方程的两边分别相加(系数互为相反数)或相减(系数相等)来消去这个未知数,得到一个一元一次方程,进而求得二元一次方程组的解.
合作探究
例3 用加减法解方程组:
①
②
解: ①×2得:
4x - 6y =8. ③
③ + ②得:
7x =14,
x =2.
把x =1代入①,得:
y =0.
∴原方程组的解是
x =2,
y =0.
{
典例精析3 加减法解找系数最小公倍数的二元一次方程组
同一未知数的系数 时,利用等
式的性质,使得未知数的系数 .
不相等也不互为相反数
相等或互为相反数
找系数的最小公倍数
1.用加减法解方程组:
①
②
①×3得:
所以原方程组的解是
解:
③-④得: y=2.
把y=2代入①,
解得: x=3.
②×2得:
6x+9y=36. ③
6x+8y=34. ④
巩固新知
解: ②×4得:
所以原方程组的解为
①
2.解方程组:
②
③
①+③得:7x = 35,
解得:x = 5.
把x = 5代入②得,y = 1.
4x-4y=16.
2台大收割机和5台小收割机均工作2h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
分析:题目中存在的两个等量关系:
2×(2台大收割量+5台小收割量)=______
5×(3台大收割量+2台小收割量)=______
3.6hm2
8hm2
新知二 列二元一次方程组解实际问题
合作探究
3.6
整理,得
解:设一台大收割机和一台小收割机每小时各收割小麦x hm2和y hm2.根据题意,得
②-①,得 __________
解得 x=_______
把x=_____ 代入①,得y=_______
∴这个方程组的解为
答:一台大收割机和一台小收割机每小时分别收割小麦0.4hm2和0.2hm2
4x+10y
15x+10y
8
11x=4.4
0.4
0.4
0.2
0.2
0.4
3.6
3x+2y
8
2x+5y
①
②
利用二元一次方程组解决实际问题的基本步骤是:
(1)依题意,找________关系;
(2)根据等量关系设_______;
(3)列__________;
(4)解__________;
(5)检验并作答.
等量关系
未知数
方程组
方程组
归纳小结
一条船顺流航行,每小时行20km,逆流航行,每小时行16km,求轮船在静水中的速度与水的速度.
解:设轮船在静水中的速度为xkm/h,水流的速度为ykm/h
由题意得:
解得
答:轮船在静水中的速度为18km/h,水流的速度为2km/h.
巩固新知
A
课堂练习
D
加
减
D
B
①×3-②×2
①×2+②×3
9.(8分)(海南中考)时下正是海南百香果丰收的季节,张阿姨到“海南爱心扶贫网”上选购百香果,若购买2千克“红土”百香果和1千克“黄金”百香果需付80元,若购买1千克“红土”百香果和3千克“黄金”百香果需付115元.请问这两种百香果每千克各是多少元?
加减消元法解二元一次方程组
基本思路“消元”
加减消元法解二元一次方程组的一般步骤
列二元一次方程组解实际问题
归纳新知
A
课后练习
B
1
60
7.(娄底中考)假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
再见
