8.2 消元——解二元一次方程组(第1课时) 课件(共38张PPT)
文档属性
| 名称 | 8.2 消元——解二元一次方程组(第1课时) 课件(共38张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 20:43:03 | ||
图片预览









文档简介
(共38张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第八章 二元一次方程组
8.2 消元——解二元一次方程组
第1课时 用代入法解二元一次方程组
1.掌握代入消元法解二元一次方程组的步骤.
2.了解解二元一次方程组的基本思路.
3.初步体会化归思想在数学学习中的运用.
学习目标
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
(1)如果设胜的场数是x
,则负的场数是10-x,
可得一元一次方程
;
(2)如果设胜的场数是x
,负的场数是y,
可得二元一次方程组
那么怎样解这个二元一次方程组呢?
导入新知
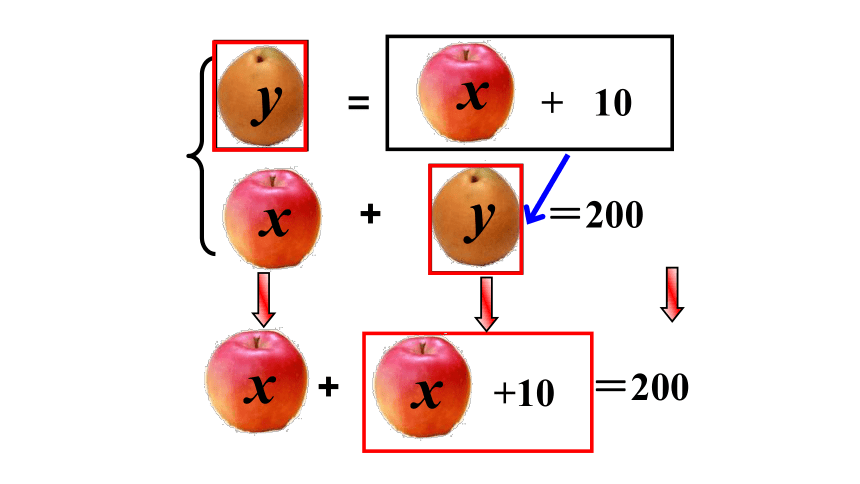
一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
新知一 代入消元法解二元一次方程组
合作探究
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
求方程组解的过程叫做解方程组.
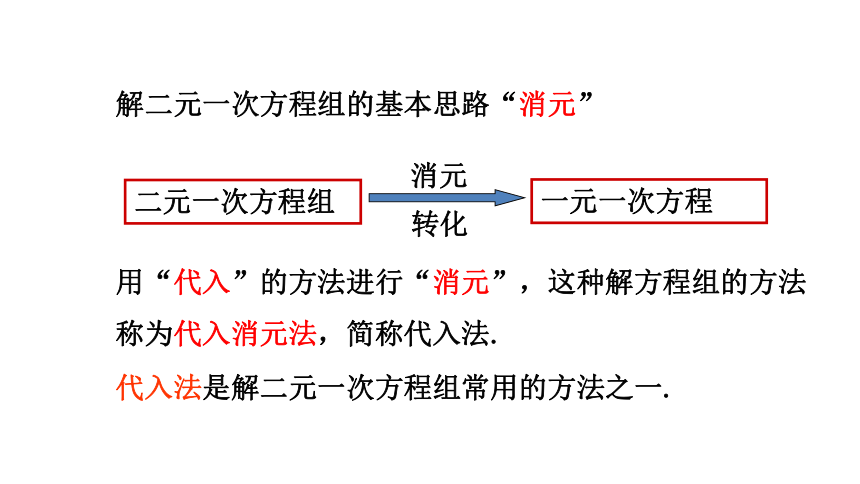
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
例1 解方程组
2x+3y=16 ①
x+4y=13 ②
解:由② ,得x=13 - 4y. ③
将③代入① ,得 2(13 - 4y)+3y=16,
26 –8y +3y =16,
-5y= -10, y=2.
将y=2代入③ ,得x=5.
所以原方程组的解是
x=5,
y=2.
典例精析1 利用代入消元法解二元一次方程组
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
归纳小结
例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
分析:等量关系:
(1)大瓶数
小瓶数
(2)大瓶所装消毒液
小瓶所装消毒液
总生产量.
典例精析2 利用二元一次方程组解答实际问题
合作探究
解:设这些消毒液应该分装x大瓶、y小瓶.
根据题意可列方程组:
③
①
由 得: .
把 代入 得: .
③
②
解得:x=20000.
把x=20000代入 得:y=50000.
③
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
í
ì
=
+
=
22500000.
250
500
2
5
y
x
y,
x
二元一次方程组
消去
一元一次方程
变形
代入
解得
解得
用
代替
,消去未知数
50 000
y
=
代入消元法的思路
用代入消元法解二元一次方程组时,尽量选取未知数系数的绝对值是1的方程进行变形;若未知数系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
方法点拨
累死我了
真的 !
他们各驮多少包裹
根据对话解答问题.
你还累 这么大的个才比我多驮两个.
哼,我从你背上拿来一个,我的包裹数就是你的2倍!
巩固新知
解:设马驼了x个包裹,骆驼驼了y个包裹,由题意得:
解得:
答:马驼了5个包裹,骆驼驼了7个包裹.
B
课堂练习
D
A
D
D
7.(4分)已知二元一次方程x-5y=1,
用含x的代数式表示y为 ;
用含y的代数式表示x为__________________.
代入消元法解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
归纳新知
D
课后练习
2.有大小两种船,1艘大船与4艘小船一次可以载乘客46名,2艘大船与3艘小船一次可以载乘客57名.绵阳市仙海湖某船家有3艘大船与6艘小船,一次可以载游客的人数为( )
A.129名 B.120名
C.108名 D.96名
D
3x-2y=-1
5
-1
8.儿童节期间,文具商店搞促销活动,同时购买一个书包和一个文具盒可以打8折优惠,比标价省13.2元.已知书包标价比文具盒标价的3倍少6元,那么书包和文具盒的标价各是多少元?
9. (1)如下表,方程组①,方程组②,方程组③……是
按照一定规律排列的一列方程组,将方程组②的解填在表中的空白处.
14
19
⑤
(2)观察①,②,③式方程组的每个方程的等号左边无变化,等号右边的数逐渐增大3,再观察x,y的值,x的值逐渐增大2,y的值逐渐增大1,由所给条件知a=14,b=19.该方程组是(1)中所给的一列方程组中第⑤个方程组
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第八章 二元一次方程组
8.2 消元——解二元一次方程组
第1课时 用代入法解二元一次方程组
1.掌握代入消元法解二元一次方程组的步骤.
2.了解解二元一次方程组的基本思路.
3.初步体会化归思想在数学学习中的运用.
学习目标
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
(1)如果设胜的场数是x
,则负的场数是10-x,
可得一元一次方程
;
(2)如果设胜的场数是x
,负的场数是y,
可得二元一次方程组
那么怎样解这个二元一次方程组呢?
导入新知
一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
新知一 代入消元法解二元一次方程组
合作探究
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
求方程组解的过程叫做解方程组.
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
例1 解方程组
2x+3y=16 ①
x+4y=13 ②
解:由② ,得x=13 - 4y. ③
将③代入① ,得 2(13 - 4y)+3y=16,
26 –8y +3y =16,
-5y= -10, y=2.
将y=2代入③ ,得x=5.
所以原方程组的解是
x=5,
y=2.
典例精析1 利用代入消元法解二元一次方程组
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
归纳小结
例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
分析:等量关系:
(1)大瓶数
小瓶数
(2)大瓶所装消毒液
小瓶所装消毒液
总生产量.
典例精析2 利用二元一次方程组解答实际问题
合作探究
解:设这些消毒液应该分装x大瓶、y小瓶.
根据题意可列方程组:
③
①
由 得: .
把 代入 得: .
③
②
解得:x=20000.
把x=20000代入 得:y=50000.
③
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
í
ì
=
+
=
22500000.
250
500
2
5
y
x
y,
x
二元一次方程组
消去
一元一次方程
变形
代入
解得
解得
用
代替
,消去未知数
50 000
y
=
代入消元法的思路
用代入消元法解二元一次方程组时,尽量选取未知数系数的绝对值是1的方程进行变形;若未知数系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.
方法点拨
累死我了
真的 !
他们各驮多少包裹
根据对话解答问题.
你还累 这么大的个才比我多驮两个.
哼,我从你背上拿来一个,我的包裹数就是你的2倍!
巩固新知
解:设马驼了x个包裹,骆驼驼了y个包裹,由题意得:
解得:
答:马驼了5个包裹,骆驼驼了7个包裹.
B
课堂练习
D
A
D
D
7.(4分)已知二元一次方程x-5y=1,
用含x的代数式表示y为 ;
用含y的代数式表示x为__________________.
代入消元法解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
归纳新知
D
课后练习
2.有大小两种船,1艘大船与4艘小船一次可以载乘客46名,2艘大船与3艘小船一次可以载乘客57名.绵阳市仙海湖某船家有3艘大船与6艘小船,一次可以载游客的人数为( )
A.129名 B.120名
C.108名 D.96名
D
3x-2y=-1
5
-1
8.儿童节期间,文具商店搞促销活动,同时购买一个书包和一个文具盒可以打8折优惠,比标价省13.2元.已知书包标价比文具盒标价的3倍少6元,那么书包和文具盒的标价各是多少元?
9. (1)如下表,方程组①,方程组②,方程组③……是
按照一定规律排列的一列方程组,将方程组②的解填在表中的空白处.
14
19
⑤
(2)观察①,②,③式方程组的每个方程的等号左边无变化,等号右边的数逐渐增大3,再观察x,y的值,x的值逐渐增大2,y的值逐渐增大1,由所给条件知a=14,b=19.该方程组是(1)中所给的一列方程组中第⑤个方程组
https://www.21cnjy.com/help/help_extract.php
