8.3 实际问题与二元一次方程组(第1课时)课件(共47张PPT)
文档属性
| 名称 | 8.3 实际问题与二元一次方程组(第1课时)课件(共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 21:45:08 | ||
图片预览











文档简介
(共47张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第八章 二元一次方程组
8.3 实际问题与二元一次方程组
第1课时
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.
2.学会利用二元一次方程组解决几何、行程问题.
3.经历用方程组解决实际图形问题的过程,体会方程组是刻画现实世界的有效数学模型.
学习目标
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李大叔估计的准确吗?
新知一 列二元一次方程组解答较简单问题
合作探究
问题1 题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;每头小牛1天需用的饲料.
问题2 题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为xkg和ykg,
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组,得: x= ,
y= .
20
5
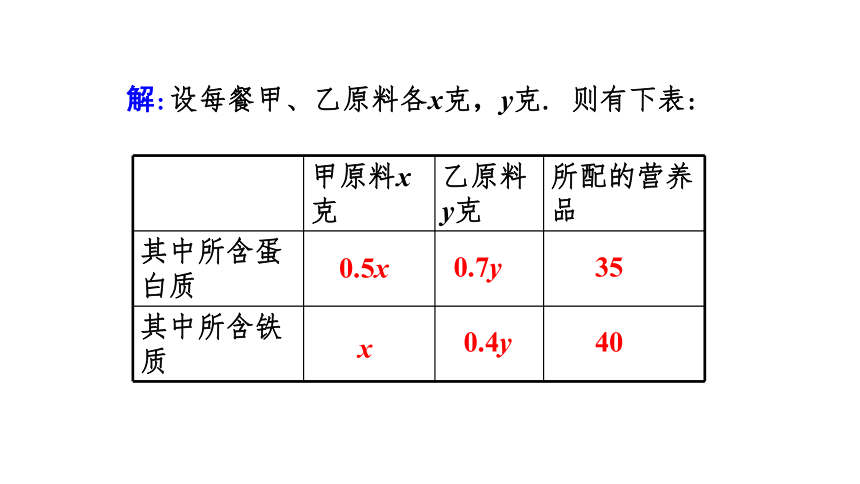
例 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要
典例精析 列二元一次方程组解答数量问题
解:设每餐甲、乙原料各x克,y克. 则有下表:
甲原料x克 乙原料y克 所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
根据题意,得方程组
化简,得
①- ②,得 5y=150
y=30
把y=30代入①,得x=28
答:每餐甲原料28克,乙原料30克恰好满足病人的需要.
0.5x+0.7y=35,
x+0.4y=40.
5x+7y=350, ①
5x+2y=200. ②
用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元法
归纳小结
某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.
巩固新知
解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,
x+2y=1680,
2x+y=2280.
解得:
x=960,
y=360.
(2)若7个餐厅同时开放,则有
5×960+2×360=5520,
答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐. (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐.
5520>5300.
依题意得
据统计资料,甲、乙两种作物的单位面积产量的比1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
新知二 列二元一次方程组解答几何问题
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
A
D
C
B
合作探究
这里研究的实际上是什么问题?
把一个长方形分成两个小长方形有哪些分割方式?
方法1
竖着画,把长分成两段,则宽不变
方法2
横着画,把宽分成两段,则长不变
长方形的面积分割
我们可以画出示意图来帮助分析
动手试着画一画
目标:甲、乙两种作物的总产量的比是3:4
问题分析
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
等量关系式有几个?
方法1
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
设AE=xm,BE=ym.
先求出两种作物的面积
SAEFD=100x
SEFCB=100y
再写出两种作物的总产量
甲:100x×1
乙:100y×2
则列方程为
100x:200y=3:4
总产量=
?
1 : 2
x
y
200m
100
如何设未知数呢?
则列方程为
x+y=200
单位面积产量×面积
方法1
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
根据题意列方程组为
100x:200y=3:4.
x
y
200m
100m
x+y=200,
解得
x=120,
y=80.
你觉得该如何答题比较完整呢?
甲种作物
乙种
作物
解:
过点E作EF⊥AB,交CD于点F.
设AE=xm,BE=ym.
答:将这块土地分为长120m,宽100m和长100m,宽80m的
两个小长方形分别种植甲、乙两种作物.
方法1
解法一
横着画,把宽分成两段,则长不变
A
D
C
B
E
x
y
F
x+y=100,
乙种作物
甲种作物
解:过点E作EF⊥BC,交BC于点F. 设DE=xm,AE=ym.
200x:400y=3:4.
200y
200x
x=60,
y=40.
解得
根据题意列方程组为
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
方法2
解法二
例 某校现有校舍20000m2计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2 )
解:设应拆除旧校舍xm2,建造新校舍ym2
拆
20000m2
新建
典例精析 列二元一次方程组解答几何问题
由题意得:
解得:
答:应该拆除2000m2旧校舍,建造8000m2新校舍.
8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位:cm)
60
x+y=60,
x=3y .
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
巩固新知
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
新知三 列二元一次方程组解答行程问题
合作探究
分析:小华到学校的路分成两段,一段为平路,一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡路的时间=________,
走上坡路的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡路长y m.
根据题意,可列方程组:
解方程组,得
所以小明家到学校的距离为700m.
方法二(间接设元法)
平路 距离 坡路距离
上学
放学
解:设小华下坡路所花时间为xmin,上坡路所花时间为ymin.
根据题意,可列方程组:
解方程组,得
所以小明家到学校的距离为700m.
故 平路距离:60×(10-5)=300(m)
坡路距离:80×5=400(m)
例 张强与李毅二人分别从相距 20 千米的两地出发,相向而行.若张强比李毅早出发 30 分钟,那么在李毅出发后 2 小时,他们相遇;如果他们同时出发,那么 1 小时后两人还相距 11 千米.求张强、李毅每小时各走多少千米?
典例精析 列二元一次方程组解答行程问题
2y千米
张强2.5小时走的路程
李毅2小时走的路程
11千米
0.5x千米
2x千米
(1)
A
B
x千米
y千米
(2)
A
B
解:设张强、李毅每小时各走x, y千米,由题意得
答:张强、李毅每小时各走4, 5千米.
分析:如下图(1)、(2)所示
巴广高速公路在5月10日正式通车,从巴中到广元全长约126 km,一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行6 km,设小汽车和货车的速度分别为x km/h、y km/h,则下列方程组正确的是( )
A. B.
C. D.
D
巩固新知
D
1.(4分)(嘉兴中考)中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为( )
课堂练习
2.(4分)(深圳中考)某旅店一共有70个房间,大房间每间住8个人,小房间每间住6个人,若一共480个学生刚好注满,设有大房间x个,小房间y个,则所列方程组正确的是( )
A
3.(5分)湘潭盘龙大观园开园啦!其中杜鹃园的门票售价为:成人票每张50元,儿童票每张30元.如果某日杜鹃园售出门票100张,门票收入共4 000元,那么当日售出成人票____张.
50
4.(8分)(吉林中考)被誉为“最美高铁”的长春至珲春城际铁路经过许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为342 km,隧道累计长度的2倍比桥梁累计长度多36 km,求隧道累计长度与桥梁累计长度.
5.(5分)现用190张铁皮做盒子,每张铁皮做8个盒身或做22个盒底,而一个盒身与两个盒底配成一个盒子,设用x张铁皮做盒身,y张铁皮做盒底,则可列方程组为( )
A
6.(6分)某服装加工厂接受生产学生校服的任务,
已知每3米长的布料可做上衣2件或裤子3条,
1件上衣和1条裤子配为一套.
计划用750米的布料生产校服,应用____米布料生产上衣,
用____米布料做裤子才能恰好配套,共能生产____套.
450
300
300
7.(8分)某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个.2个甲种部件和3个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据2个等量关系列出方程组
检验作答
解方程组:
代入法;
加减法.
几何问题
归纳新知
C
课后练习
2.小明的爸爸骑着摩托车带着小明在公路上匀速行驶,
小明每隔一段时间看到的时程碑上的数如下:
则12:00时看到的两位数是( )
A.24 B.42 C.51 D.15
D
3.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为x,十位数字为y,则根据题意可列方程组为______________.
4.为准备母亲节礼物,同学们委托小明用其支付宝余额团购鲜花或礼盒.每束鲜花的售价相同,每份礼盒的售价也相同.若团购15束鲜花和18份礼盒,余额差80元;若团购18束鲜花和15份礼盒,余额剩70元.若团购19束鲜花和14份礼盒,则支付宝余额剩____元.
120
5.(徐州中考)4月9日上午8时,2017徐州国际马拉松赛鸣枪开跑,一名34岁的男子带着他的两个孩子参加了比赛,下面是两个孩子与记者的对话:
根据对话内容,请你用方程的知识帮记者求
出哥哥和妹妹的年龄.
6.某景点的门票价格如表:
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,
(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,
则一共支付1118元;如果两班都以班联合起来作为一个团体购票,
则只需花费816元.
(1)两个班各有多少名学生?约了多少钱?
购票人数/人 1~50 51~100 100以上
每人门票/元 12 10 8
7.(烟台中考)亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第八章 二元一次方程组
8.3 实际问题与二元一次方程组
第1课时
1.能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.
2.学会利用二元一次方程组解决几何、行程问题.
3.经历用方程组解决实际图形问题的过程,体会方程组是刻画现实世界的有效数学模型.
学习目标
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李大叔估计的准确吗?
新知一 列二元一次方程组解答较简单问题
合作探究
问题1 题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;每头小牛1天需用的饲料.
问题2 题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为xkg和ykg,
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组,得: x= ,
y= .
20
5
例 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要
典例精析 列二元一次方程组解答数量问题
解:设每餐甲、乙原料各x克,y克. 则有下表:
甲原料x克 乙原料y克 所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
根据题意,得方程组
化简,得
①- ②,得 5y=150
y=30
把y=30代入①,得x=28
答:每餐甲原料28克,乙原料30克恰好满足病人的需要.
0.5x+0.7y=35,
x+0.4y=40.
5x+7y=350, ①
5x+2y=200. ②
用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元法
归纳小结
某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.
巩固新知
解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,
x+2y=1680,
2x+y=2280.
解得:
x=960,
y=360.
(2)若7个餐厅同时开放,则有
5×960+2×360=5520,
答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐. (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐.
5520>5300.
依题意得
据统计资料,甲、乙两种作物的单位面积产量的比1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
新知二 列二元一次方程组解答几何问题
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
A
D
C
B
合作探究
这里研究的实际上是什么问题?
把一个长方形分成两个小长方形有哪些分割方式?
方法1
竖着画,把长分成两段,则宽不变
方法2
横着画,把宽分成两段,则长不变
长方形的面积分割
我们可以画出示意图来帮助分析
动手试着画一画
目标:甲、乙两种作物的总产量的比是3:4
问题分析
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
等量关系式有几个?
方法1
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
设AE=xm,BE=ym.
先求出两种作物的面积
SAEFD=100x
SEFCB=100y
再写出两种作物的总产量
甲:100x×1
乙:100y×2
则列方程为
100x:200y=3:4
总产量=
?
1 : 2
x
y
200m
100
如何设未知数呢?
则列方程为
x+y=200
单位面积产量×面积
方法1
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
根据题意列方程组为
100x:200y=3:4.
x
y
200m
100m
x+y=200,
解得
x=120,
y=80.
你觉得该如何答题比较完整呢?
甲种作物
乙种
作物
解:
过点E作EF⊥AB,交CD于点F.
设AE=xm,BE=ym.
答:将这块土地分为长120m,宽100m和长100m,宽80m的
两个小长方形分别种植甲、乙两种作物.
方法1
解法一
横着画,把宽分成两段,则长不变
A
D
C
B
E
x
y
F
x+y=100,
乙种作物
甲种作物
解:过点E作EF⊥BC,交BC于点F. 设DE=xm,AE=ym.
200x:400y=3:4.
200y
200x
x=60,
y=40.
解得
根据题意列方程组为
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
方法2
解法二
例 某校现有校舍20000m2计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2 )
解:设应拆除旧校舍xm2,建造新校舍ym2
拆
20000m2
新建
典例精析 列二元一次方程组解答几何问题
由题意得:
解得:
答:应该拆除2000m2旧校舍,建造8000m2新校舍.
8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少 (单位:cm)
60
x+y=60,
x=3y .
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
巩固新知
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
新知三 列二元一次方程组解答行程问题
合作探究
分析:小华到学校的路分成两段,一段为平路,一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡路的时间=________,
走上坡路的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡路长y m.
根据题意,可列方程组:
解方程组,得
所以小明家到学校的距离为700m.
方法二(间接设元法)
平路 距离 坡路距离
上学
放学
解:设小华下坡路所花时间为xmin,上坡路所花时间为ymin.
根据题意,可列方程组:
解方程组,得
所以小明家到学校的距离为700m.
故 平路距离:60×(10-5)=300(m)
坡路距离:80×5=400(m)
例 张强与李毅二人分别从相距 20 千米的两地出发,相向而行.若张强比李毅早出发 30 分钟,那么在李毅出发后 2 小时,他们相遇;如果他们同时出发,那么 1 小时后两人还相距 11 千米.求张强、李毅每小时各走多少千米?
典例精析 列二元一次方程组解答行程问题
2y千米
张强2.5小时走的路程
李毅2小时走的路程
11千米
0.5x千米
2x千米
(1)
A
B
x千米
y千米
(2)
A
B
解:设张强、李毅每小时各走x, y千米,由题意得
答:张强、李毅每小时各走4, 5千米.
分析:如下图(1)、(2)所示
巴广高速公路在5月10日正式通车,从巴中到广元全长约126 km,一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45分钟相遇,相遇时小汽车比货车多行6 km,设小汽车和货车的速度分别为x km/h、y km/h,则下列方程组正确的是( )
A. B.
C. D.
D
巩固新知
D
1.(4分)(嘉兴中考)中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为( )
课堂练习
2.(4分)(深圳中考)某旅店一共有70个房间,大房间每间住8个人,小房间每间住6个人,若一共480个学生刚好注满,设有大房间x个,小房间y个,则所列方程组正确的是( )
A
3.(5分)湘潭盘龙大观园开园啦!其中杜鹃园的门票售价为:成人票每张50元,儿童票每张30元.如果某日杜鹃园售出门票100张,门票收入共4 000元,那么当日售出成人票____张.
50
4.(8分)(吉林中考)被誉为“最美高铁”的长春至珲春城际铁路经过许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为342 km,隧道累计长度的2倍比桥梁累计长度多36 km,求隧道累计长度与桥梁累计长度.
5.(5分)现用190张铁皮做盒子,每张铁皮做8个盒身或做22个盒底,而一个盒身与两个盒底配成一个盒子,设用x张铁皮做盒身,y张铁皮做盒底,则可列方程组为( )
A
6.(6分)某服装加工厂接受生产学生校服的任务,
已知每3米长的布料可做上衣2件或裤子3条,
1件上衣和1条裤子配为一套.
计划用750米的布料生产校服,应用____米布料生产上衣,
用____米布料做裤子才能恰好配套,共能生产____套.
450
300
300
7.(8分)某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个.2个甲种部件和3个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据2个等量关系列出方程组
检验作答
解方程组:
代入法;
加减法.
几何问题
归纳新知
C
课后练习
2.小明的爸爸骑着摩托车带着小明在公路上匀速行驶,
小明每隔一段时间看到的时程碑上的数如下:
则12:00时看到的两位数是( )
A.24 B.42 C.51 D.15
D
3.一个两位数的十位数字与个位数字的和是8,把这个两位数加上18,结果恰好成为数字对调后组成的两位数,求这个两位数.设个位数字为x,十位数字为y,则根据题意可列方程组为______________.
4.为准备母亲节礼物,同学们委托小明用其支付宝余额团购鲜花或礼盒.每束鲜花的售价相同,每份礼盒的售价也相同.若团购15束鲜花和18份礼盒,余额差80元;若团购18束鲜花和15份礼盒,余额剩70元.若团购19束鲜花和14份礼盒,则支付宝余额剩____元.
120
5.(徐州中考)4月9日上午8时,2017徐州国际马拉松赛鸣枪开跑,一名34岁的男子带着他的两个孩子参加了比赛,下面是两个孩子与记者的对话:
根据对话内容,请你用方程的知识帮记者求
出哥哥和妹妹的年龄.
6.某景点的门票价格如表:
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,
(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,
则一共支付1118元;如果两班都以班联合起来作为一个团体购票,
则只需花费816元.
(1)两个班各有多少名学生?约了多少钱?
购票人数/人 1~50 51~100 100以上
每人门票/元 12 10 8
7.(烟台中考)亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
https://www.21cnjy.com/help/help_extract.php
