8.3 实际问题与二元一次方程组(第2课时)课件(共43张PPT)
文档属性
| 名称 | 8.3 实际问题与二元一次方程组(第2课时)课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 21:26:17 | ||
图片预览









文档简介
(共43张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第八章 二元一次方程组
8.3 实际问题与二元一次方程组
第2课时
1.学会运用二元一次方程组解决较复杂的实际问题.
2.进一步经历和体验方程组解决实际问题的过程,提高运用方程组解决问题的能力.
学习目标
如图,化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费
97 200元.这批产品的销售款比原料费与运输费的和多多少元?
新知 列二元一次方程组解答较复杂问题
典例精析1 列二元一次方程组解答运费问题
合作探究
问题1 要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
问题2 本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
一类是公路运费,铁路运费,价值;
另一类是产品数量,原料数量.
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
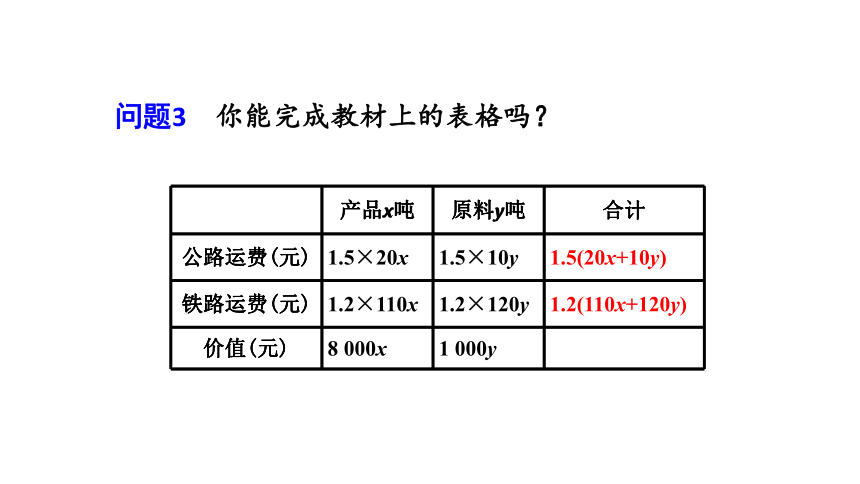
问题3 你能完成教材上的表格吗?
产品x吨 原料y吨 合计
公路运费(元) 1.5×20x 1.5×10y 1.5(20x+10y)
铁路运费(元) 1.2×110x 1.2×120y 1.2(110x+120y)
价值(元) 8 000x 1 000y
问题4 你发现等量关系了吗?如何列方程组并求解?
是原方程组的解.
解:先化简,得
②
①
由①,得
代入③ ,得
③
代入② ,得
问题5 这个实际问题的答案是什么?
销售款:8 000×300=2 400 000元;
原料费:1 000×400=400 000元;
运输费:15 000+97 200=112 200元.
2400000-400000-112200=1887800元.
这批产品的销售款比原料费与运输费的和多1 887 800元.
思考:
(1)在什么情况下考虑选择设间接未知数?
当直接将所求的结果当作未知数无法列出方程时,考虑选择设间接未知数.
(2)如何更好地分析数量关系比较复杂的实际问题?
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题的答案
一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表(两次两种货车都满载):
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,你能算出货主应付运费多少元吗?
巩固新知
解:设甲、乙两种货车每辆每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5,
5x+ 6y=35.
总运费为:
30×(3x+ 5y)=30×(3×4+ 5×2.5)=735(元).
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
答:货主应付运费735元.
例2 某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成
(1)你认为哪种方案获利最多,为什么 (2)本题解出之后,你还能提出哪些问题
典例精析2 列二元一次方程组解答利润问题
合作探究
其余5吨直接销售,获利500×5=2500(元),
∴共获利:8000+2500=10500(元).
方案二:设生产奶片用x天,生产酸奶用y天
另:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶
x+y=4,
x+3y=9.
x+y=9,
方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=8000 (元)
1.5×1×2000+2.5×3×1200
=12000 (元).
∴共获利:
1.5×2000+7.5×1200
=3000+9000=12000 (元).
∴共获利:
x=1.5,
y=2.5.
解得:
x=1.5,
y=7.5.
解得:
北京和上海都有某种仪器可供外地使用,其中北京可提供10台,上海可提供4台.已知重庆需要8台,武汉需要6台,从北京、上海将仪器运往重庆、武汉的费用如下表所示.有关部门计划用8000元运送这些仪器,请你设计一种方案,使武汉、重庆能得到所需仪器,而且运费正好够用.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
巩固新知
解:设从北京运往武汉x台,则运往重庆(10-x)台,设从上海运往武汉y台,则运往重庆(4-y)台,
解方程组得
x=4,
y=2.
x+ y=6,
400x+ 300y+800(10-x)+ 500(4-y)=8000.
答:从北京运往武汉4台,运往重庆6台,从上海运往武汉2台,运往重庆2台.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
例3 某车间每天能生产甲种零件600个或乙种零件300个,
或丙种零件500个,甲、乙、丙三种零件各1个就可以配成一套,要在63天内的生产中,使生产的零件全部成套,问甲、乙、丙三种零件各应生产几天?
典例精析3 列二元一次方程组解答配套问题
解:设甲零件生产x天,乙零件生产y天,则丙零件生产(63-x-y)天,根据题意,得
所以63-x-y=18.
答:甲、乙、丙三种零件各应生产15天、30天和18天.
解得
合作探究
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应各安排多少名工人生产螺钉和螺母?
分析: 将题中出现的量在表格中呈现
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
巩固新知
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
总结:解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
D
课堂练习
B
2.(5分)(牡丹江中考)如图,在长为15,宽为12的矩形中,
有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为( )
A.35 B.45 C.55 D.65
3.(4分)一个长方形的长减少15 cm,宽增加6 cm,就变成一个正方形,
并且这两个图形的面积相等,则原长方形的面积为____cm2.
5.(5分)如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,
再将图中的阴影部分剪拼成一个长方形,如图②.
这个拼成的长方形的长为30,宽为20,则图②中Ⅱ部分的面积是____.
100
100
4.(8分)如图,在长为10 m,宽为8 m的长方形空地上,
沿平行于长方形边的方向分割出三个形状、
大小完全一样的小长方形花圃(阴影部分),求其中一个长方形的长和宽.
5.(4分)(东营中考)小岩打算购买气球装扮学校“毕业典礼”
活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,
但同一种气球的价格相同.由于会场布置需要,
购买时以一束(4个气球)为单位,
已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
A.19元 B.18元 C.16元 D.15元
B
6.(4分)请根据图中提供的信息,回答下列问题:
一个暖瓶单价为____元,一个水杯的单价为____元.
30
8
7.(4分)小方、小红和小军三人玩飞镖游戏,各投四支飞镖,
规定在同一圆环内得分相同,中靶和得分情况如图,
若设掷中A区、B区一次的得分分别为x分、y分,
则依题意可列方程组得____________,则小红的得分为____分.
32
8.(8分)根据图中的信息,求梅花鹿和长颈鹿现在的高度.
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
通过本课时的学习,需要我们掌握:
2.这种处理问题的过程可以进一步概括为:
归纳新知
1.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图①;小红看见了,说“我也来试一试”结果小红七拼八凑,拼成了如图②那样的正方形,中间还留下了一个洞,恰好是边长为3 mm的小正方形,则每个小长方形的面积为( )
A.120 mm2 B.135 mm2 C.108 mm2 D.96 mm2
B
课后练习
80
3.餐馆里把塑料凳整齐地叠放在一起(如图),
根据图中的信息计算有20张同样塑料凳整齐地叠放在一起时的
高度是____cm.
80
4.(宿迁中考)下面3个天平左盘中“△”“□”分别表示
两种质量不同的物体,则第三个天平右盘中砝码的质量为____.
10
5.某药业集团生产的某种药品包装盒的侧面展开图。如图,如果长方体盒子的长比宽多4 cm,求这种药品包装盒的体积.
6.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高____cm,放入一个大球水面升高____cm;
(2)如果要使水面上升到50 cm,应放入大球、小球各多少个?
2
3
7.某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A,B两种长方体形状的无盖纸盒.现有正方形纸板140张,长方形纸板360张,刚好全部用完,问能做成多少个A型盒子?多少个B型盒子?
根据两位同学所列的方程组,请你分别指出未知数x,y表示的意义:
甲:x表示________________,
y表示__________________;
乙:x表示___________________________,
y表示________________________________;
A型盒子个数
B型盒子个数
A型纸盒中正方形纸板的个数
B型纸盒中正方形纸板的个数
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 · 数学· 七年级(下)
第八章 二元一次方程组
8.3 实际问题与二元一次方程组
第2课时
1.学会运用二元一次方程组解决较复杂的实际问题.
2.进一步经历和体验方程组解决实际问题的过程,提高运用方程组解决问题的能力.
学习目标
如图,化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费
97 200元.这批产品的销售款比原料费与运输费的和多多少元?
新知 列二元一次方程组解答较复杂问题
典例精析1 列二元一次方程组解答运费问题
合作探究
问题1 要求“这批产品的销售款比原料费与运输费的和多多少元?”我们必须知道什么?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们必须知道产品的数量和原料的数量.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
问题2 本题涉及的量较多,这种情况下常用列表的方式来处理,列表直观、简洁.本题涉及哪两类量呢?
一类是公路运费,铁路运费,价值;
另一类是产品数量,原料数量.
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
问题3 你能完成教材上的表格吗?
产品x吨 原料y吨 合计
公路运费(元) 1.5×20x 1.5×10y 1.5(20x+10y)
铁路运费(元) 1.2×110x 1.2×120y 1.2(110x+120y)
价值(元) 8 000x 1 000y
问题4 你发现等量关系了吗?如何列方程组并求解?
是原方程组的解.
解:先化简,得
②
①
由①,得
代入③ ,得
③
代入② ,得
问题5 这个实际问题的答案是什么?
销售款:8 000×300=2 400 000元;
原料费:1 000×400=400 000元;
运输费:15 000+97 200=112 200元.
2400000-400000-112200=1887800元.
这批产品的销售款比原料费与运输费的和多1 887 800元.
思考:
(1)在什么情况下考虑选择设间接未知数?
当直接将所求的结果当作未知数无法列出方程时,考虑选择设间接未知数.
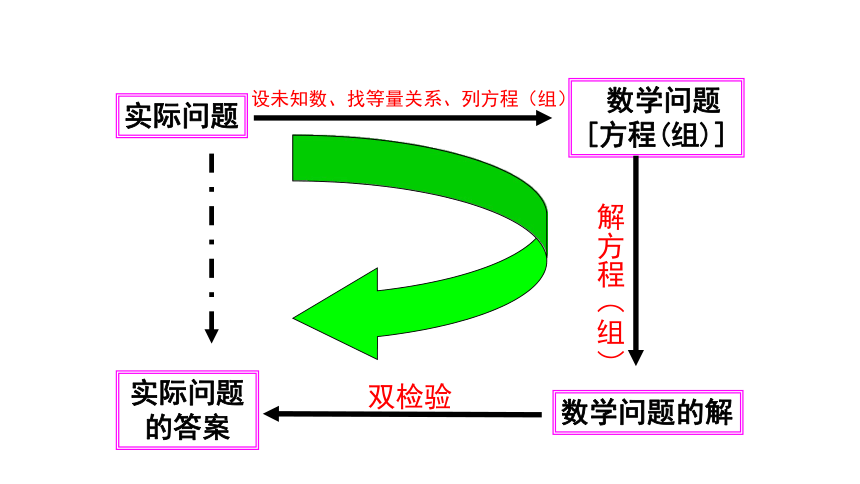
(2)如何更好地分析数量关系比较复杂的实际问题?
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题的答案
一批货物要运往某地,货主准备用汽车运输公司的甲乙两种货车,已知过去两次租用这两种货车的情况如下表(两次两种货车都满载):
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
现租用该公司3辆甲种货车和5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,你能算出货主应付运费多少元吗?
巩固新知
解:设甲、乙两种货车每辆每次分别运货x吨、y吨,
解得
x=4,
y=2.5.
2x+ 3y=15.5,
5x+ 6y=35.
总运费为:
30×(3x+ 5y)=30×(3×4+ 5×2.5)=735(元).
第一次 第二次
甲种货车的车辆数(辆) 2 5
乙种货车的车辆数(辆) 3 6
累计运货吨数(吨) 15.5 35
答:货主应付运费735元.
例2 某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成
(1)你认为哪种方案获利最多,为什么 (2)本题解出之后,你还能提出哪些问题
典例精析2 列二元一次方程组解答利润问题
合作探究
其余5吨直接销售,获利500×5=2500(元),
∴共获利:8000+2500=10500(元).
方案二:设生产奶片用x天,生产酸奶用y天
另:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶
x+y=4,
x+3y=9.
x+y=9,
方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=8000 (元)
1.5×1×2000+2.5×3×1200
=12000 (元).
∴共获利:
1.5×2000+7.5×1200
=3000+9000=12000 (元).
∴共获利:
x=1.5,
y=2.5.
解得:
x=1.5,
y=7.5.
解得:
北京和上海都有某种仪器可供外地使用,其中北京可提供10台,上海可提供4台.已知重庆需要8台,武汉需要6台,从北京、上海将仪器运往重庆、武汉的费用如下表所示.有关部门计划用8000元运送这些仪器,请你设计一种方案,使武汉、重庆能得到所需仪器,而且运费正好够用.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
巩固新知
解:设从北京运往武汉x台,则运往重庆(10-x)台,设从上海运往武汉y台,则运往重庆(4-y)台,
解方程组得
x=4,
y=2.
x+ y=6,
400x+ 300y+800(10-x)+ 500(4-y)=8000.
答:从北京运往武汉4台,运往重庆6台,从上海运往武汉2台,运往重庆2台.
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
例3 某车间每天能生产甲种零件600个或乙种零件300个,
或丙种零件500个,甲、乙、丙三种零件各1个就可以配成一套,要在63天内的生产中,使生产的零件全部成套,问甲、乙、丙三种零件各应生产几天?
典例精析3 列二元一次方程组解答配套问题
解:设甲零件生产x天,乙零件生产y天,则丙零件生产(63-x-y)天,根据题意,得
所以63-x-y=18.
答:甲、乙、丙三种零件各应生产15天、30天和18天.
解得
合作探究
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应各安排多少名工人生产螺钉和螺母?
分析: 将题中出现的量在表格中呈现
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
巩固新知
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
总结:解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
D
课堂练习
B
2.(5分)(牡丹江中考)如图,在长为15,宽为12的矩形中,
有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为( )
A.35 B.45 C.55 D.65
3.(4分)一个长方形的长减少15 cm,宽增加6 cm,就变成一个正方形,
并且这两个图形的面积相等,则原长方形的面积为____cm2.
5.(5分)如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,
再将图中的阴影部分剪拼成一个长方形,如图②.
这个拼成的长方形的长为30,宽为20,则图②中Ⅱ部分的面积是____.
100
100
4.(8分)如图,在长为10 m,宽为8 m的长方形空地上,
沿平行于长方形边的方向分割出三个形状、
大小完全一样的小长方形花圃(阴影部分),求其中一个长方形的长和宽.
5.(4分)(东营中考)小岩打算购买气球装扮学校“毕业典礼”
活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,
但同一种气球的价格相同.由于会场布置需要,
购买时以一束(4个气球)为单位,
已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
A.19元 B.18元 C.16元 D.15元
B
6.(4分)请根据图中提供的信息,回答下列问题:
一个暖瓶单价为____元,一个水杯的单价为____元.
30
8
7.(4分)小方、小红和小军三人玩飞镖游戏,各投四支飞镖,
规定在同一圆环内得分相同,中靶和得分情况如图,
若设掷中A区、B区一次的得分分别为x分、y分,
则依题意可列方程组得____________,则小红的得分为____分.
32
8.(8分)根据图中的信息,求梅花鹿和长颈鹿现在的高度.
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
通过本课时的学习,需要我们掌握:
2.这种处理问题的过程可以进一步概括为:
归纳新知
1.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图①;小红看见了,说“我也来试一试”结果小红七拼八凑,拼成了如图②那样的正方形,中间还留下了一个洞,恰好是边长为3 mm的小正方形,则每个小长方形的面积为( )
A.120 mm2 B.135 mm2 C.108 mm2 D.96 mm2
B
课后练习
80
3.餐馆里把塑料凳整齐地叠放在一起(如图),
根据图中的信息计算有20张同样塑料凳整齐地叠放在一起时的
高度是____cm.
80
4.(宿迁中考)下面3个天平左盘中“△”“□”分别表示
两种质量不同的物体,则第三个天平右盘中砝码的质量为____.
10
5.某药业集团生产的某种药品包装盒的侧面展开图。如图,如果长方体盒子的长比宽多4 cm,求这种药品包装盒的体积.
6.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高____cm,放入一个大球水面升高____cm;
(2)如果要使水面上升到50 cm,应放入大球、小球各多少个?
2
3
7.某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A,B两种长方体形状的无盖纸盒.现有正方形纸板140张,长方形纸板360张,刚好全部用完,问能做成多少个A型盒子?多少个B型盒子?
根据两位同学所列的方程组,请你分别指出未知数x,y表示的意义:
甲:x表示________________,
y表示__________________;
乙:x表示___________________________,
y表示________________________________;
A型盒子个数
B型盒子个数
A型纸盒中正方形纸板的个数
B型纸盒中正方形纸板的个数
https://www.21cnjy.com/help/help_extract.php
