7 .1两条直线的位置关系(第1课时) 课件(共26张PPT)
文档属性
| 名称 | 7 .1两条直线的位置关系(第1课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 00:00:00 | ||
图片预览


文档简介
(共26张PPT)
2022年春鲁教版数学
六年级下册数学精品课件
《两条直线的位置关系》
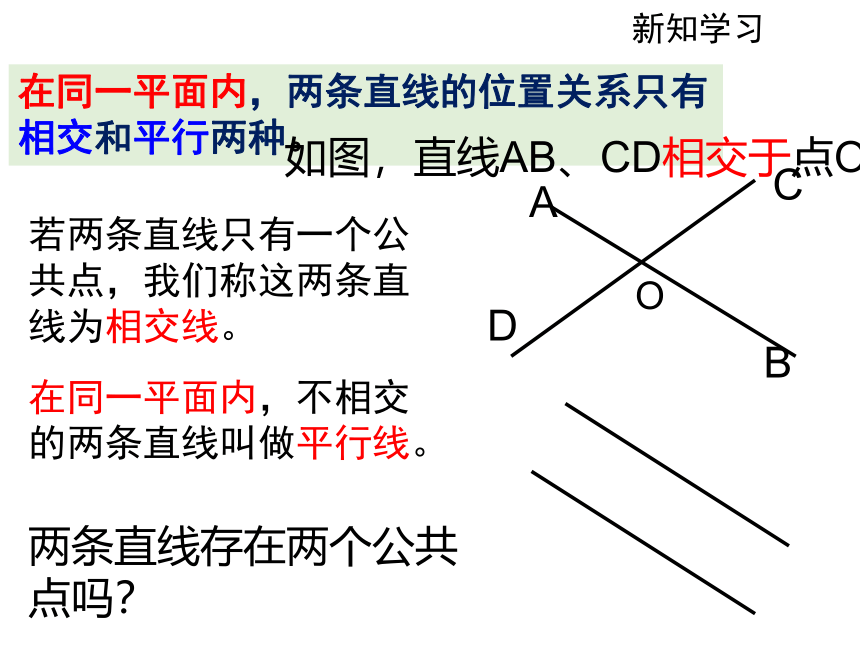
若两条直线只有一个公共点,我们称这两条直线为相交线。
在同一平面内,不相交的两条直线叫做平行线。
在同一平面内,两条直线的位置关系只有相交和平行两种。
O
新知学习
两条直线存在两个公共点吗?
A
B
C
D
如图,直线AB、CD相交于点O
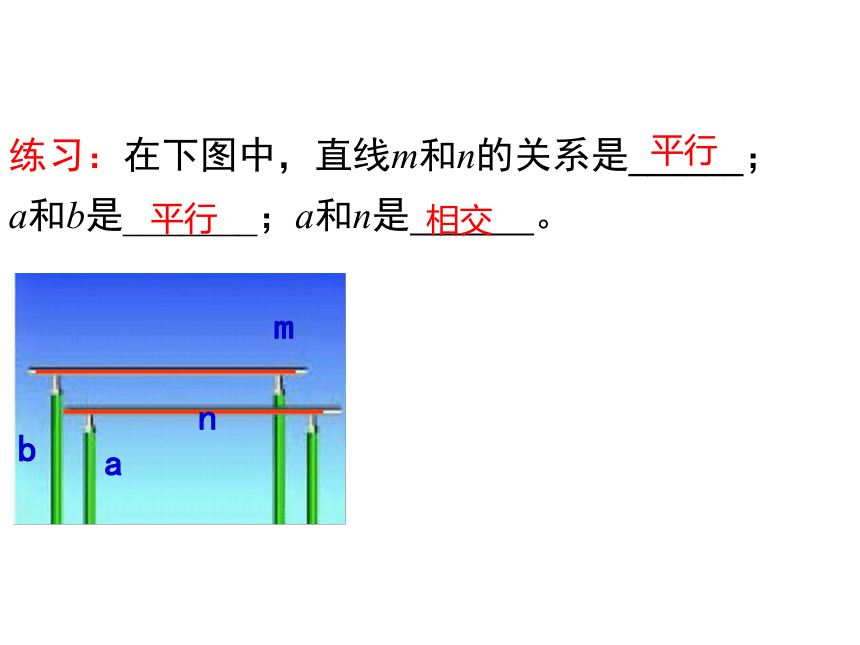
练习:在下图中,直线m和n的关系是______;a和b是_______;a和n是 。
m
n
a
b
平行
平行
相交
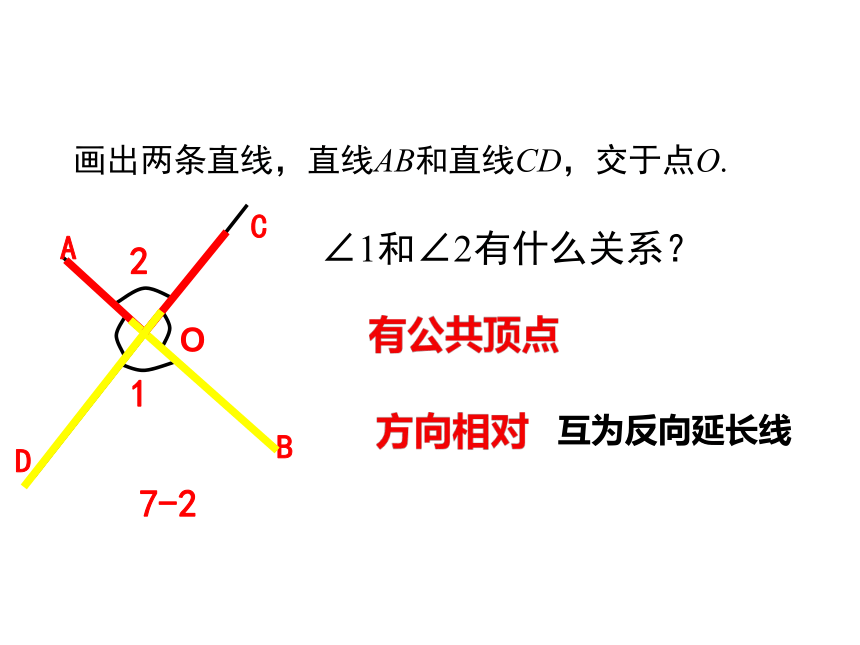
画出两条直线,直线AB和直线CD,交于点O.
2
1
7-2
A
B
C
D
∠1和∠2有什么关系?
有公共顶点
方向相对
互为反向延长线
O
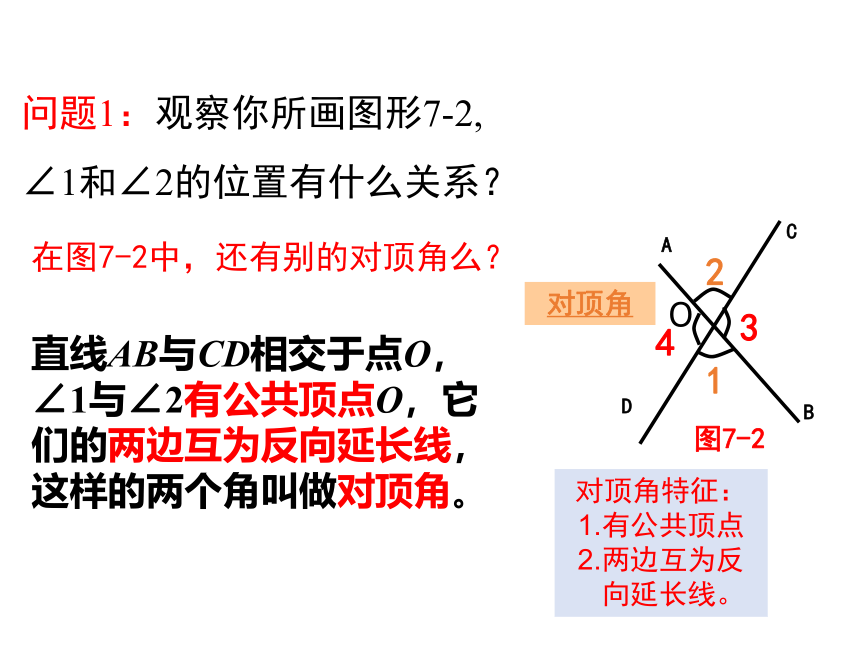
问题1:观察你所画图形7-2,
∠1和∠2的位置有什么关系?
3
2
1
4
图7-2
A
B
C
D
对顶角
O
在图7-2中,还有别的对顶角么?
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角。
对顶角特征:
1.有公共顶点
2.两边互为反
向延长线。
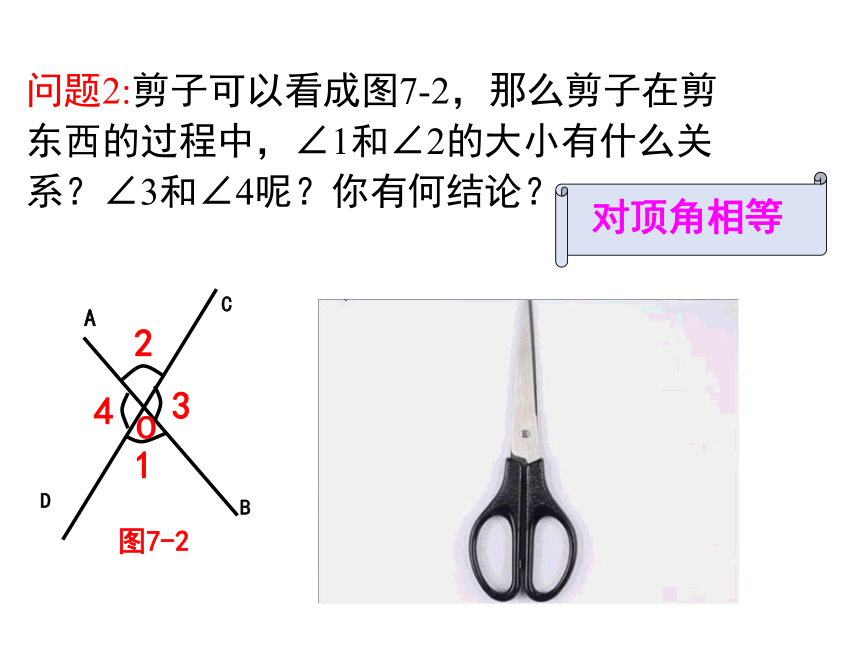
问题2:剪子可以看成图7-2,那么剪子在剪东西的过程中,∠1和∠2的大小有什么关系?∠3和∠4呢?你有何结论?
对顶角相等
3
2
1
4
图7-2
A
B
C
D
O
3
2
1
4
图7-2
A
B
C
D
O
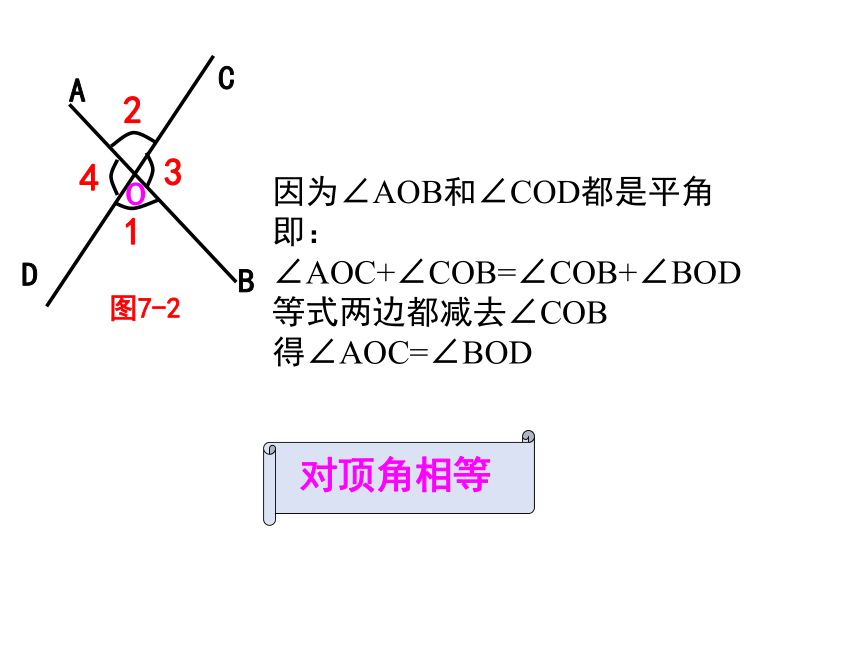
因为∠AOB和∠COD都是平角
即:
∠AOC+∠COB=∠COB+∠BOD
等式两边都减去∠COB
得∠AOC=∠BOD
对顶角相等
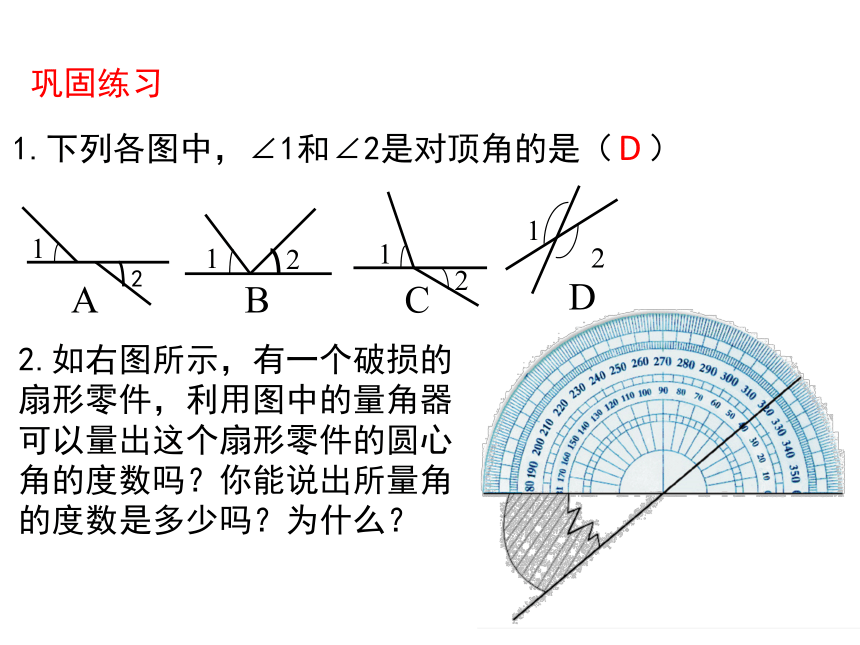
巩固练习
1
2
1
2
1
2
1
2
A
B
C
D
1.下列各图中,∠1和∠2是对顶角的是( )
2.如右图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
D
问题3:在右图中,∠1与∠3有什么数量关系?
如果两个角的和是180°,那么称这两个角互为补角。或称这两个角互补,其中一个角是另一个角的补角。
3
4
D
2
1
O
B
C
A
3
4
如果两个角的和是90 °,那么称这两个角互为余角。或称这两个角互余,其中一个角是另一个角的余角。
注意:互余与互补是指两个角度数关系,与它们的位置无关。
巩固练习1:
巩固练习2:
下列说法中,正确的有 (填序号)
① 已知∠A=40°,则∠A的余角等于500
②若∠1+∠2=90°,则∠1和∠2互为余角。
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角。
④若∠A=40 26′,则∠A的补角=139°34′
⑤一个角的补角必为钝角。
①②④
图7-3
打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图7-3抽象成成图7-4,ON与DC交于点O,∠DON=∠CON=90°,∠1=∠2
2
D
C
O
1
3
4
A
N
B
图7-4
图7-3
在图7-4中∠DON=∠CON=90°,∠1=∠2
问题1:哪些角互为补角?哪些角互为余角?
2
D
C
O
1
3
4
A
N
B
图7-4
补角:∠DOA与∠AOC,∠DON与∠NOC,
∠DOB与∠BOC
余角:∠1与∠3,∠2与∠4,
∠1与∠4,∠2与∠3
图7-3
在图7-4中
问题2:∠3与∠4有什么关系?为什么?
2
D
C
O
1
3
4
A
N
B
图7-4
2
D
C
O
1
3
4
A
N
B
图7-4
∵∠1+_____=90°,∠2+_____=90°
∴∠3=90°-_____ ,∠4=90°-_____
∵∠1=_____
∴∠3=∠4
已知:∠DON=∠CON=90°,∠1=∠2
∠3
∠4
∠1
∠2
∠2
图7-3
在图7-4中
问题3:∠AOC与∠BOD有什么关系?为什么?
你还能得到哪些结论?
2
D
C
O
1
3
4
A
N
B
图7-4
2
D
C
O
1
3
4
A
N
B
图7-4
已知:∠DON=∠CON=90°,∠1=∠2
∵∠1+∠AOC=_______°,
∠2+∠BOD=_______°
∴∠AOC=_______°-∠1 ,
∠BOD=_______°-∠2
∵∠_____=∠______
∴∠AOC=∠BOD
180
180
180
180
1
2
2
D
C
O
1
3
4
A
N
B
∵∠1=∠2
∵∠1+∠3=90°,∠2+∠4=90°
∴∠3=∠4
∵∠1+∠AOC=180°,∠2+∠BOD=180°
∴∠AOC=∠BOD
同角或等角的余角相等
同角或等角的补角相等
2
1
O
B
C
A
3
4
问题1:
①.因为∠1+∠2=90 ,∠2+∠3=90 ,
所以∠1= ______ ,理由是 ____________ .
② 因为∠1+∠2=180 ,∠2+∠3=180 ,
所以∠1= ________ ,理由是 ____________ .
巩固练习3
∠3
同角的余角相等
∠3
同角的补角相等
问题2:①你手中的三角板,如图.
则∠A是∠B的 。
变式训练:在①的基础上,做∠CDA=90°,则∠A的余角有哪几个?为什么?
C
A
B
问题2图
C
A
B
变式训练图
D
余角
∠ACD,∠B
问题3:已知:直线AB与CD交于点O, ∠EOD=90°,回答下列问题:
1.∠AOE的余角是 补角是 。
2.∠AOC的余角是 ;补角是 ;对顶角是 。
C
A
B
D
O
E
∠AOC,∠BOD
∠BOE
∠AOE
∠AOD,∠BOC
∠BOD
你学到了哪些知识?
一、定义:
1、对顶角
2、互为补角,余角
二、性质:
对顶角相等
同角或等角的余角相等
同角或等角的补角相等
(1)互为补角的两个角可以都是锐角吗?
可以都是直角吗?可以都是钝角吗?
(2)一个锐角的补角比这个角的余角大900对吗?
思考
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
六年级下册数学精品课件
《两条直线的位置关系》
若两条直线只有一个公共点,我们称这两条直线为相交线。
在同一平面内,不相交的两条直线叫做平行线。
在同一平面内,两条直线的位置关系只有相交和平行两种。
O
新知学习
两条直线存在两个公共点吗?
A
B
C
D
如图,直线AB、CD相交于点O
练习:在下图中,直线m和n的关系是______;a和b是_______;a和n是 。
m
n
a
b
平行
平行
相交
画出两条直线,直线AB和直线CD,交于点O.
2
1
7-2
A
B
C
D
∠1和∠2有什么关系?
有公共顶点
方向相对
互为反向延长线
O
问题1:观察你所画图形7-2,
∠1和∠2的位置有什么关系?
3
2
1
4
图7-2
A
B
C
D
对顶角
O
在图7-2中,还有别的对顶角么?
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角。
对顶角特征:
1.有公共顶点
2.两边互为反
向延长线。
问题2:剪子可以看成图7-2,那么剪子在剪东西的过程中,∠1和∠2的大小有什么关系?∠3和∠4呢?你有何结论?
对顶角相等
3
2
1
4
图7-2
A
B
C
D
O
3
2
1
4
图7-2
A
B
C
D
O
因为∠AOB和∠COD都是平角
即:
∠AOC+∠COB=∠COB+∠BOD
等式两边都减去∠COB
得∠AOC=∠BOD
对顶角相等
巩固练习
1
2
1
2
1
2
1
2
A
B
C
D
1.下列各图中,∠1和∠2是对顶角的是( )
2.如右图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
D
问题3:在右图中,∠1与∠3有什么数量关系?
如果两个角的和是180°,那么称这两个角互为补角。或称这两个角互补,其中一个角是另一个角的补角。
3
4
D
2
1
O
B
C
A
3
4
如果两个角的和是90 °,那么称这两个角互为余角。或称这两个角互余,其中一个角是另一个角的余角。
注意:互余与互补是指两个角度数关系,与它们的位置无关。
巩固练习1:
巩固练习2:
下列说法中,正确的有 (填序号)
① 已知∠A=40°,则∠A的余角等于500
②若∠1+∠2=90°,则∠1和∠2互为余角。
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角。
④若∠A=40 26′,则∠A的补角=139°34′
⑤一个角的补角必为钝角。
①②④
图7-3
打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图7-3抽象成成图7-4,ON与DC交于点O,∠DON=∠CON=90°,∠1=∠2
2
D
C
O
1
3
4
A
N
B
图7-4
图7-3
在图7-4中∠DON=∠CON=90°,∠1=∠2
问题1:哪些角互为补角?哪些角互为余角?
2
D
C
O
1
3
4
A
N
B
图7-4
补角:∠DOA与∠AOC,∠DON与∠NOC,
∠DOB与∠BOC
余角:∠1与∠3,∠2与∠4,
∠1与∠4,∠2与∠3
图7-3
在图7-4中
问题2:∠3与∠4有什么关系?为什么?
2
D
C
O
1
3
4
A
N
B
图7-4
2
D
C
O
1
3
4
A
N
B
图7-4
∵∠1+_____=90°,∠2+_____=90°
∴∠3=90°-_____ ,∠4=90°-_____
∵∠1=_____
∴∠3=∠4
已知:∠DON=∠CON=90°,∠1=∠2
∠3
∠4
∠1
∠2
∠2
图7-3
在图7-4中
问题3:∠AOC与∠BOD有什么关系?为什么?
你还能得到哪些结论?
2
D
C
O
1
3
4
A
N
B
图7-4
2
D
C
O
1
3
4
A
N
B
图7-4
已知:∠DON=∠CON=90°,∠1=∠2
∵∠1+∠AOC=_______°,
∠2+∠BOD=_______°
∴∠AOC=_______°-∠1 ,
∠BOD=_______°-∠2
∵∠_____=∠______
∴∠AOC=∠BOD
180
180
180
180
1
2
2
D
C
O
1
3
4
A
N
B
∵∠1=∠2
∵∠1+∠3=90°,∠2+∠4=90°
∴∠3=∠4
∵∠1+∠AOC=180°,∠2+∠BOD=180°
∴∠AOC=∠BOD
同角或等角的余角相等
同角或等角的补角相等
2
1
O
B
C
A
3
4
问题1:
①.因为∠1+∠2=90 ,∠2+∠3=90 ,
所以∠1= ______ ,理由是 ____________ .
② 因为∠1+∠2=180 ,∠2+∠3=180 ,
所以∠1= ________ ,理由是 ____________ .
巩固练习3
∠3
同角的余角相等
∠3
同角的补角相等
问题2:①你手中的三角板,如图.
则∠A是∠B的 。
变式训练:在①的基础上,做∠CDA=90°,则∠A的余角有哪几个?为什么?
C
A
B
问题2图
C
A
B
变式训练图
D
余角
∠ACD,∠B
问题3:已知:直线AB与CD交于点O, ∠EOD=90°,回答下列问题:
1.∠AOE的余角是 补角是 。
2.∠AOC的余角是 ;补角是 ;对顶角是 。
C
A
B
D
O
E
∠AOC,∠BOD
∠BOE
∠AOE
∠AOD,∠BOC
∠BOD
你学到了哪些知识?
一、定义:
1、对顶角
2、互为补角,余角
二、性质:
对顶角相等
同角或等角的余角相等
同角或等角的补角相等
(1)互为补角的两个角可以都是锐角吗?
可以都是直角吗?可以都是钝角吗?
(2)一个锐角的补角比这个角的余角大900对吗?
思考
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
