7 .1两条直线的位置关系(复习) 课件(共23张PPT)
文档属性
| 名称 | 7 .1两条直线的位置关系(复习) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
2022年春鲁教版数学
六年级下册数学精品课件
两条直线的位置关系
复习课
1.在同一平面内,两条直线的位置关系可能是( )
A.相交、平行 B.相交、垂直
C.平行、垂直 D.平行、相交、垂直
回顾:同一平面内两条直线的位置关系
A
若两条直线只有一个公共点,我们称这两条直线为相交线。
在同一平面内,不相交的两条直线叫做平行线。
O
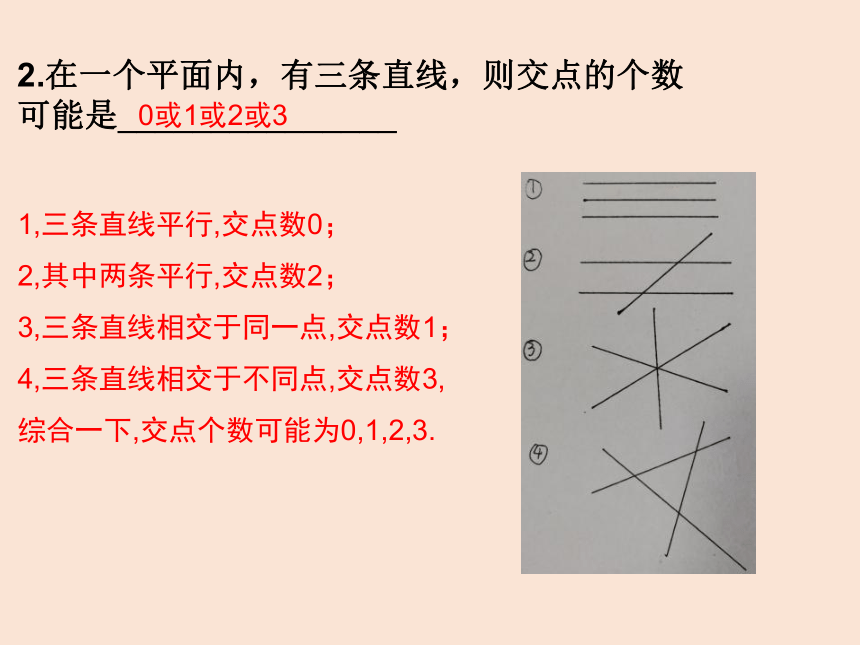
1,三条直线平行,交点数0;
2,其中两条平行,交点数2;
3,三条直线相交于同一点,交点数1;
4,三条直线相交于不同点,交点数3,
综合一下,交点个数可能为0,1,2,3.
2.在一个平面内,有三条直线,则交点的个数
可能是_______________
0或1或2或3
2
1
7-2
A
B
C
D
有公共顶点
方向相对
互为反向延长线
O
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角。
对顶角相等
对顶角是怎样形成的?
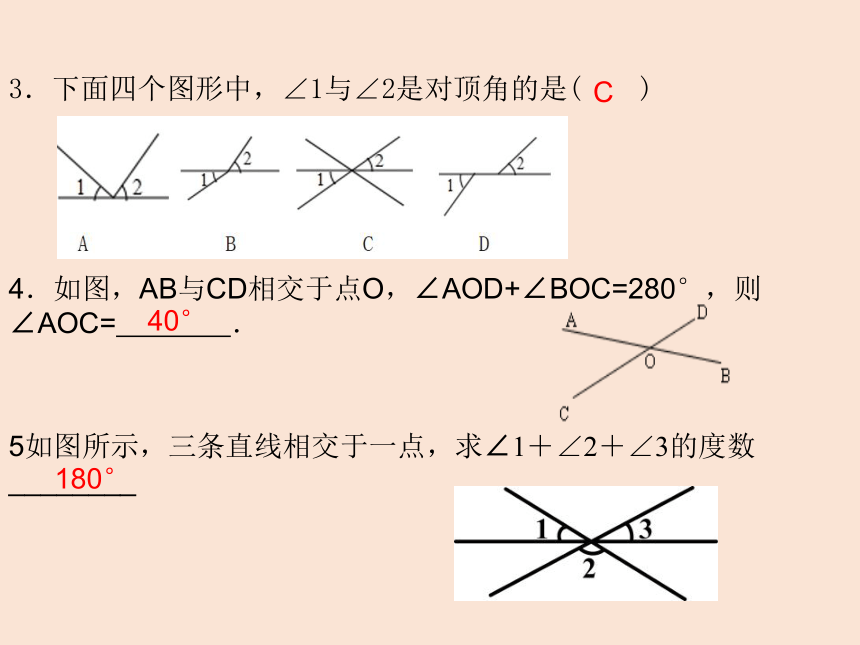
3.下面四个图形中,∠1与∠2是对顶角的是( )
C
4.如图,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC= .
40°
5如图所示,三条直线相交于一点,求∠1+∠2+∠3的度数________
180°
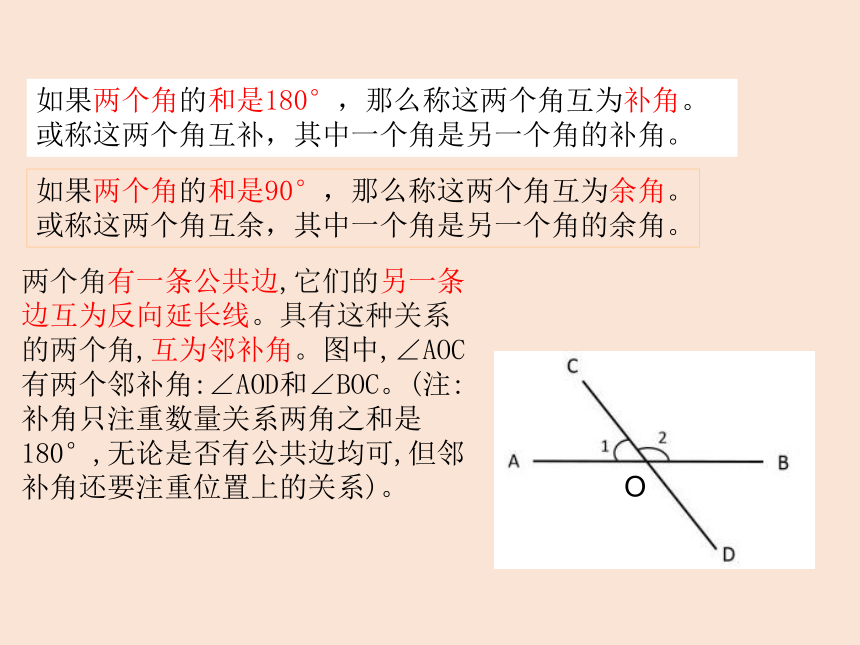
如果两个角的和是180°,那么称这两个角互为补角。或称这两个角互补,其中一个角是另一个角的补角。
如果两个角的和是90°,那么称这两个角互为余角。
或称这两个角互余,其中一个角是另一个角的余角。
两个角有一条公共边,它们的另一条边互为反向延长线。具有这种关系的两个角,互为邻补角。图中,∠AOC有两个邻补角:∠AOD和∠BOC。(注:补角只注重数量关系两角之和是180°,无论是否有公共边均可,但邻补角还要注重位置上的关系)。
O
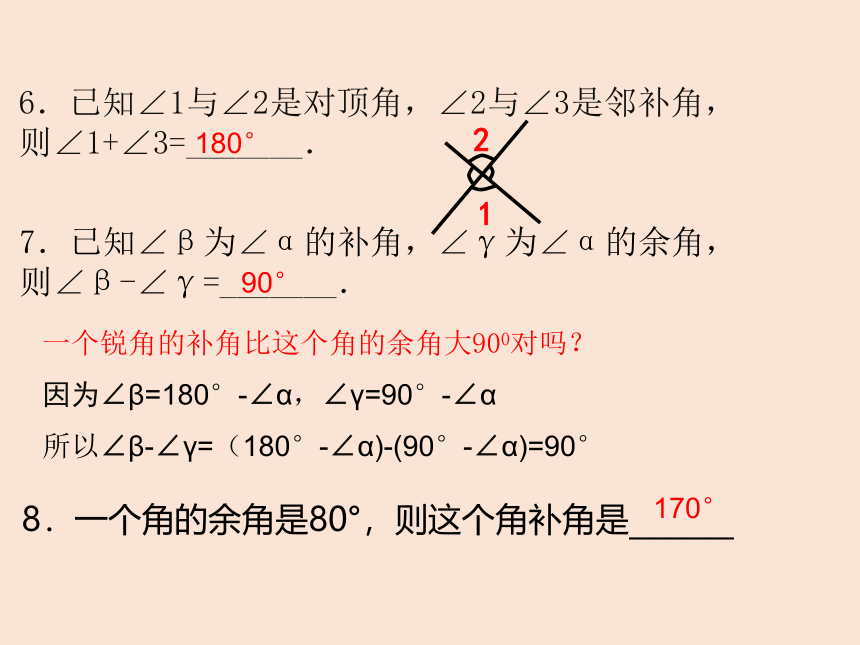
6.已知∠1与∠2是对顶角,∠2与∠3是邻补角,则∠1+∠3=_______.
7.已知∠β为∠α的补角,∠γ为∠α的余角,
则∠β-∠γ=_______.
一个锐角的补角比这个角的余角大900对吗?
因为∠β=180°-∠α,∠γ=90°-∠α
所以∠β-∠γ=(180°-∠α)-(90°-∠α)=90°
180°
90°
8.一个角的余角是80°,则这个角补角是_______
170°
2
1
9.一个角的补角是它的余角的4倍,则这个角等于___.
解:设这个角为 x, 则这个角的补角为(180°-x), 则这个角的余角为(90°-x).根据题意可得:
180°-x=4(90°-x)
解得:x=60°
60°
10.若一个角的余角与它的补角的和为210°,则这个角的余角等于______.
11.若一个角的补角与这个角的余角的度数之比是3:1,
则这个角等于————————
解:设这个角余角为 x, 则这个角的补角为90°+ x
x+90°+ x=210°
60°
45°
解:设这个角为 x,这个角的补角为(180°-x),这个角的余角为(90°-x)
据题意可得:
(180°-x)=3(90°-x)
同角或等角的余角相等
同角或等角的补角相等
定义:两条直线相交成四个角,如果有一个角是直角,那么称两条直线互相垂直。其中的一条直线叫做另一条直线的垂线。
o
l
m
垂线的性质:
·
A
·
A
m
m
平面内,
过一点有且只有一条直线与已知直线垂直。
平面内,一条直线的垂线有无数条。
m
P
O
C
B
A
线段PO的长度叫做点P到直线m的距离
直线外一点与直线上各点所连的所有线段中垂线段最短
线段PO叫做
点P到直线m的垂线段
分别找出图中互相垂直的线段:
AO⊥OC
OD⊥OB
BC ⊥CA BC ⊥DC
BC ⊥DA CE ⊥AC
CE ⊥DC CE ⊥DA
还有互相垂直的线段吗?
12.如图所示,已知OA⊥OB,OC⊥OD,
∠AOC︰∠BOD=1︰2,则∠BOD=________.
13.如图所示,AC⊥BC,CD⊥AB,
点A到BC边的距离是线段 的长,
点B到CD边的距离是线段 的长,
∠A的余角有 ,
和∠B相等的角有 .
120°
AC
BD
∠B,∠ACD
∠ACD
∠AOC+∠BOD=180°
14.如图,要从小河引水到村庄A,请设计并作出一最短路线,理由是___________________.
15.如图,直线a⊥b,∠1=50°,则∠2= 度.
解:∵a⊥b,( )
∴∠1+∠2+90°=180°( , )
∴∠1+∠2=90°,( )
∵∠1=50°,( )
∴∠2=90°﹣∠1=40°.
垂线段最短
40
16.如图,直线AB、CD相交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,求∠AOE和∠DOF的度数.
∵OE⊥CD,
∴∠COE=_____°(垂线定义)
∵∠AOC=∠BOD=25°( )
∴∠AOE=∠COE-________=65°
∵OF⊥AB,
∴∠FOB=______°(垂线定义 )
∴∠DOF=∠FOB+________=_____°
90
对顶角相等
∠AOC
90
∠BOD
115
17.直线AB、CD相交于O点,若∠DOE=40°,∠BOC=130°,
猜想射线OE与直线AB的位置关系,并说明理由.
∵∠BOC=130°,
∴∠AOD=∠BOC=130°( )
∵∠AOD=∠AOE+______=130°
∴∠AOE=∠AOD - _______
∵∠DOE=40°,
∴∠AOE=_____°
对顶角相等
∠DOE
∠DOE
90
所以射线OE与直线AB互相垂直
18.如图所示,将长方形纸片折叠,使点A落在点A′处,BC为折痕,BD是∠A′BE的平分线,试说明CB与BD的位置关系.
由折叠可得:
∵BD是∠A′BE的平分线
∴__________________
∵∠ABA′+∠A′BE=______°
∴∠CBD=∠A′BC+_______
=
=90°
∴CB⊥BD
180
∠A′BD
如图,点O为直线AB上一点,OC为一射线,OE平分∠AOC,OF平分∠BOC.试探究OE,OF的位置关系.
OE⊥OF
19.如图甲所示,AO⊥BO,CO⊥DO.
(1)试猜想∠AOD与∠COB在数量上是相等,互余,
还是互补的关系,你能用推理的方法说明你的猜想是否合理吗?
(2)当∠COD绕点O旋转到图乙的位置时,你原来的猜想还成立吗?
∵AO⊥BO,CO⊥DO,
∴∠AOB=∠COD=______°
∵∠AOD=∠AOB+______
∠BOC=∠COD -∠BOD
∴∠AOD+∠BOC
=(∠AOB+______)+(∠COD -∠BOD)
=∠AOB+∠COD
=_______°
90
∠BOD
∠BOD
180
∴∠AOD与∠BOC互补
1.你学到了哪些知识?
2.你学会了哪些方法?
3.你认为应注意哪些问题?
4.你还有哪些困惑?
学有所思
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
六年级下册数学精品课件
两条直线的位置关系
复习课
1.在同一平面内,两条直线的位置关系可能是( )
A.相交、平行 B.相交、垂直
C.平行、垂直 D.平行、相交、垂直
回顾:同一平面内两条直线的位置关系
A
若两条直线只有一个公共点,我们称这两条直线为相交线。
在同一平面内,不相交的两条直线叫做平行线。
O
1,三条直线平行,交点数0;
2,其中两条平行,交点数2;
3,三条直线相交于同一点,交点数1;
4,三条直线相交于不同点,交点数3,
综合一下,交点个数可能为0,1,2,3.
2.在一个平面内,有三条直线,则交点的个数
可能是_______________
0或1或2或3
2
1
7-2
A
B
C
D
有公共顶点
方向相对
互为反向延长线
O
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角。
对顶角相等
对顶角是怎样形成的?
3.下面四个图形中,∠1与∠2是对顶角的是( )
C
4.如图,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC= .
40°
5如图所示,三条直线相交于一点,求∠1+∠2+∠3的度数________
180°
如果两个角的和是180°,那么称这两个角互为补角。或称这两个角互补,其中一个角是另一个角的补角。
如果两个角的和是90°,那么称这两个角互为余角。
或称这两个角互余,其中一个角是另一个角的余角。
两个角有一条公共边,它们的另一条边互为反向延长线。具有这种关系的两个角,互为邻补角。图中,∠AOC有两个邻补角:∠AOD和∠BOC。(注:补角只注重数量关系两角之和是180°,无论是否有公共边均可,但邻补角还要注重位置上的关系)。
O
6.已知∠1与∠2是对顶角,∠2与∠3是邻补角,则∠1+∠3=_______.
7.已知∠β为∠α的补角,∠γ为∠α的余角,
则∠β-∠γ=_______.
一个锐角的补角比这个角的余角大900对吗?
因为∠β=180°-∠α,∠γ=90°-∠α
所以∠β-∠γ=(180°-∠α)-(90°-∠α)=90°
180°
90°
8.一个角的余角是80°,则这个角补角是_______
170°
2
1
9.一个角的补角是它的余角的4倍,则这个角等于___.
解:设这个角为 x, 则这个角的补角为(180°-x), 则这个角的余角为(90°-x).根据题意可得:
180°-x=4(90°-x)
解得:x=60°
60°
10.若一个角的余角与它的补角的和为210°,则这个角的余角等于______.
11.若一个角的补角与这个角的余角的度数之比是3:1,
则这个角等于————————
解:设这个角余角为 x, 则这个角的补角为90°+ x
x+90°+ x=210°
60°
45°
解:设这个角为 x,这个角的补角为(180°-x),这个角的余角为(90°-x)
据题意可得:
(180°-x)=3(90°-x)
同角或等角的余角相等
同角或等角的补角相等
定义:两条直线相交成四个角,如果有一个角是直角,那么称两条直线互相垂直。其中的一条直线叫做另一条直线的垂线。
o
l
m
垂线的性质:
·
A
·
A
m
m
平面内,
过一点有且只有一条直线与已知直线垂直。
平面内,一条直线的垂线有无数条。
m
P
O
C
B
A
线段PO的长度叫做点P到直线m的距离
直线外一点与直线上各点所连的所有线段中垂线段最短
线段PO叫做
点P到直线m的垂线段
分别找出图中互相垂直的线段:
AO⊥OC
OD⊥OB
BC ⊥CA BC ⊥DC
BC ⊥DA CE ⊥AC
CE ⊥DC CE ⊥DA
还有互相垂直的线段吗?
12.如图所示,已知OA⊥OB,OC⊥OD,
∠AOC︰∠BOD=1︰2,则∠BOD=________.
13.如图所示,AC⊥BC,CD⊥AB,
点A到BC边的距离是线段 的长,
点B到CD边的距离是线段 的长,
∠A的余角有 ,
和∠B相等的角有 .
120°
AC
BD
∠B,∠ACD
∠ACD
∠AOC+∠BOD=180°
14.如图,要从小河引水到村庄A,请设计并作出一最短路线,理由是___________________.
15.如图,直线a⊥b,∠1=50°,则∠2= 度.
解:∵a⊥b,( )
∴∠1+∠2+90°=180°( , )
∴∠1+∠2=90°,( )
∵∠1=50°,( )
∴∠2=90°﹣∠1=40°.
垂线段最短
40
16.如图,直线AB、CD相交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,求∠AOE和∠DOF的度数.
∵OE⊥CD,
∴∠COE=_____°(垂线定义)
∵∠AOC=∠BOD=25°( )
∴∠AOE=∠COE-________=65°
∵OF⊥AB,
∴∠FOB=______°(垂线定义 )
∴∠DOF=∠FOB+________=_____°
90
对顶角相等
∠AOC
90
∠BOD
115
17.直线AB、CD相交于O点,若∠DOE=40°,∠BOC=130°,
猜想射线OE与直线AB的位置关系,并说明理由.
∵∠BOC=130°,
∴∠AOD=∠BOC=130°( )
∵∠AOD=∠AOE+______=130°
∴∠AOE=∠AOD - _______
∵∠DOE=40°,
∴∠AOE=_____°
对顶角相等
∠DOE
∠DOE
90
所以射线OE与直线AB互相垂直
18.如图所示,将长方形纸片折叠,使点A落在点A′处,BC为折痕,BD是∠A′BE的平分线,试说明CB与BD的位置关系.
由折叠可得:
∵BD是∠A′BE的平分线
∴__________________
∵∠ABA′+∠A′BE=______°
∴∠CBD=∠A′BC+_______
=
=90°
∴CB⊥BD
180
∠A′BD
如图,点O为直线AB上一点,OC为一射线,OE平分∠AOC,OF平分∠BOC.试探究OE,OF的位置关系.
OE⊥OF
19.如图甲所示,AO⊥BO,CO⊥DO.
(1)试猜想∠AOD与∠COB在数量上是相等,互余,
还是互补的关系,你能用推理的方法说明你的猜想是否合理吗?
(2)当∠COD绕点O旋转到图乙的位置时,你原来的猜想还成立吗?
∵AO⊥BO,CO⊥DO,
∴∠AOB=∠COD=______°
∵∠AOD=∠AOB+______
∠BOC=∠COD -∠BOD
∴∠AOD+∠BOC
=(∠AOB+______)+(∠COD -∠BOD)
=∠AOB+∠COD
=_______°
90
∠BOD
∠BOD
180
∴∠AOD与∠BOC互补
1.你学到了哪些知识?
2.你学会了哪些方法?
3.你认为应注意哪些问题?
4.你还有哪些困惑?
学有所思
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
