7.2 探索直线平行的条件(复习) 课件(共23张PPT)
文档属性
| 名称 | 7.2 探索直线平行的条件(复习) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
2022年春鲁教版数学
六年级下册数学精品课件
《探索直线平行的条件》
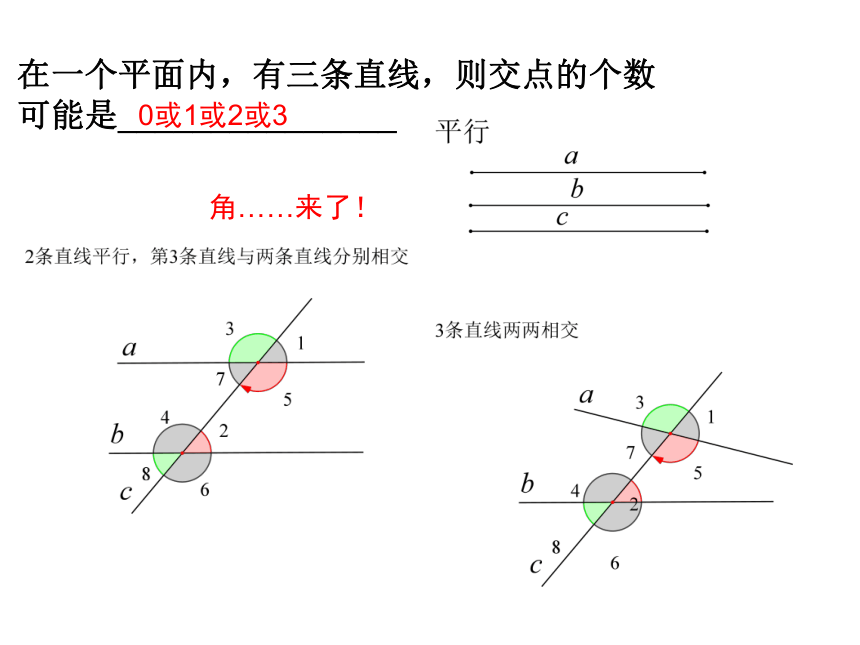
在一个平面内,有三条直线,则交点的个数
可能是_______________
0或1或2或3
角……来了!
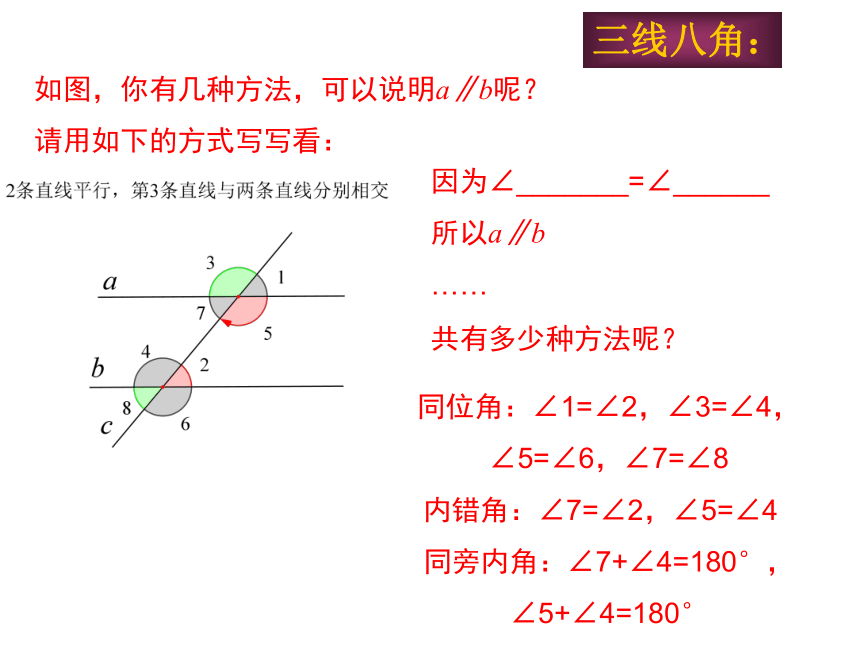
三线八角:
如图,你有几种方法,可以说明a∥b呢?
请用如下的方式写写看:
因为∠_______=∠______
所以a∥b
……
共有多少种方法呢?
同位角:∠1=∠2,∠3=∠4, ∠5=∠6,∠7=∠8
内错角:∠7=∠2,∠5=∠4
同旁内角:∠7+∠4=180°, ∠5+∠4=180°
辨析应用
1.
如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6+∠4=180°;其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
D
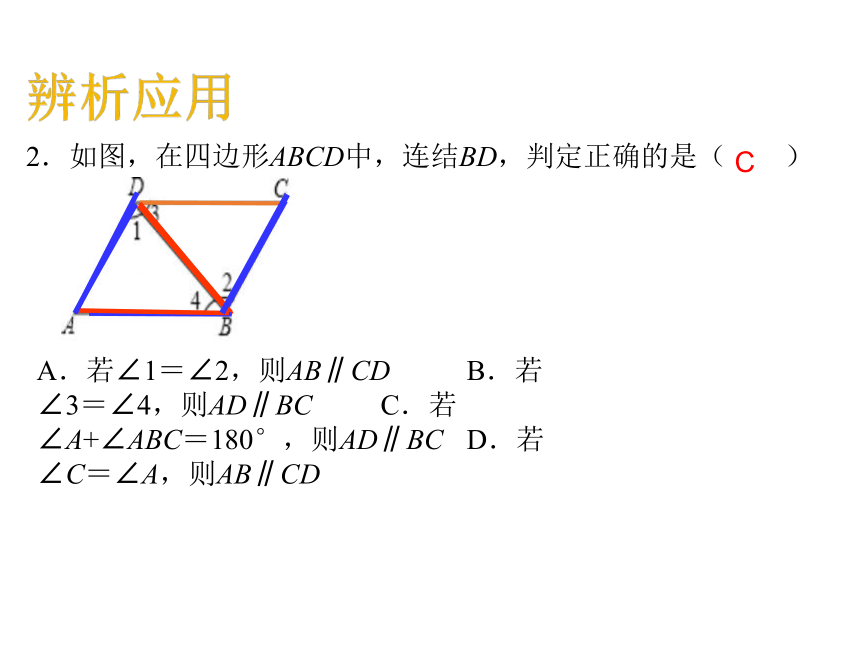
2.如图,在四边形ABCD中,连结BD,判定正确的是( )
A.若∠1=∠2,则AB∥CD B.若∠3=∠4,则AD∥BC C.若∠A+∠ABC=180°,则AD∥BC D.若∠C=∠A,则AB∥CD
辨析应用
C
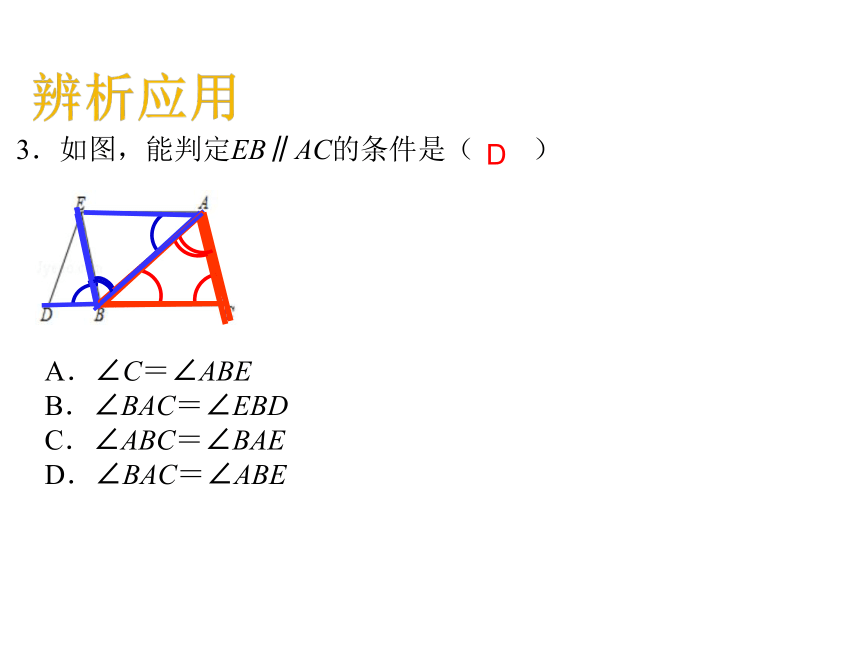
3.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠BAC=∠EBD
C.∠ABC=∠BAE
D.∠BAC=∠ABE
辨析应用
D
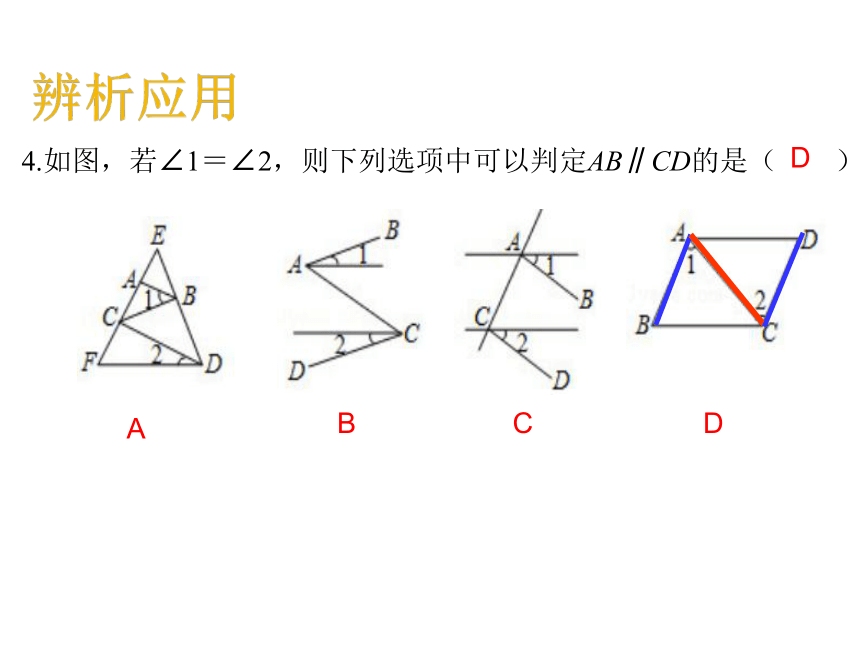
4.如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是( )
A
B
C
D
辨析应用
D
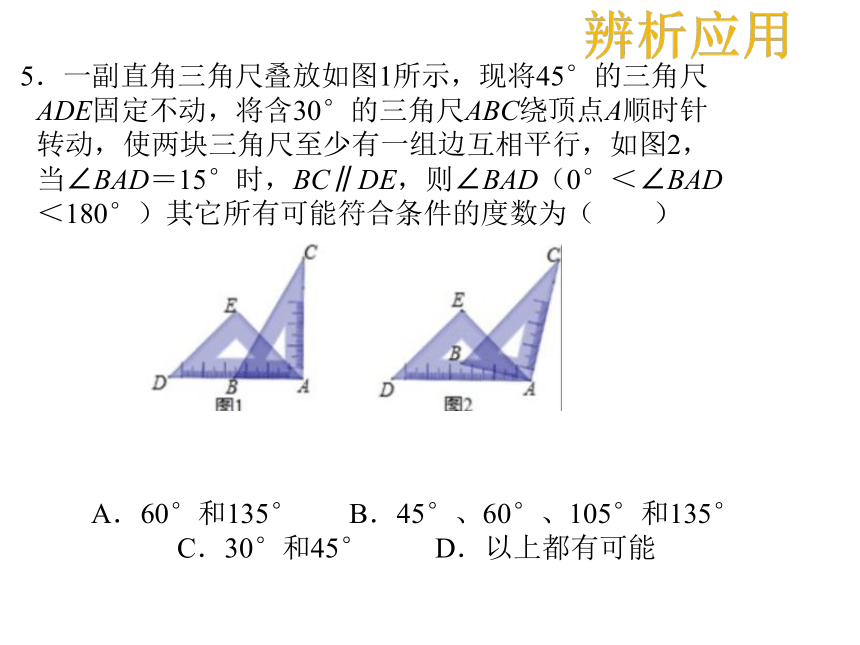
5.一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135° C.30°和45° D.以上都有可能
辨析应用
当AC∥DE时,
∠BAD=∠DAE=45
当BC∥AD时,
∠DAE=∠B=60 ;
当BC∥AE时,
∵∠EAB=∠B=60 ,
∴∠BAD=∠DAE+∠EAB=105
当AB∥DE时,
∵∠E=∠EAB=90 ,
∴∠BAD=∠DAE+∠EAB=135 .
5.一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135° C.30°和45° D.以上都有可能
辨析应用
B
6.判断题(正确的画“√”,错误的画“×”)(1)a、b、c是直线,且a∥b,b∥c,则a∥c.
(2)a、b、c是直线,且a⊥b,b⊥c,则a⊥c.
辨析应用
√ 平行于同一条直线的两条直线互相平行
垂直于同一条直线的两条直线互相平行 ×
同一平面内
7.如图,直线a、b被直线c所截,∠2=56°,则当∠1=____ 时,a∥b.
8.如图,如果希望直线c∥d,那么需要添加的条件是: .
辨析应用
124°
∠1=∠2
或∠3=∠4
9.如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 .
辨析应用
8°
10.如图,a,b,c三根木棒钉在一起,∠1=70°,∠2=100°,现将木棒a、b同时顺时针旋转一周,速度分别为17度/秒和2度/秒,则 秒后木棒a,b平行.
辨析应用
解:设t秒后木棒a,b平行,依题意有100°﹣17°t=70°﹣2°t, 解得t=2.
所以2秒后木棒a,b平行.
11.如图,直线a,点B,点C.(1)过点B画直线a的平行线,能画几条?(2)过点C画直线a的平行线,它与过点B的平行线平行吗?
辨析应用
12.如图,∠ACB=90°,∠A=35°,∠BCD=55°.
试说明:AB∥CD.
辨析应用
解:∵∠ACB=90°,
∠A=35°,∴∠B=_____°,∵∠BCD=55°,∴_____=__________,∴CD∥AB( __________ , 两直线平行 )
55
∠B
∠BCD
内错角相等
13.如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
辨析应用
方法一
证明:∵∠1=55°(已知),∴∠CNM=______°(对顶角相等),∵ ________(已知),∴_________+______=180°(等式的性质),∴AB∥CD(同旁内角互补,两直线平行).
55
∠2=125°
∠CNM
∠2
13.
如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
辨析应用
方法二
证明:∵∠1=55°(已知),∴∠DNM=______°(邻补角的定义),∵ ____________(已知),∴____________=______(等式的性质),∴AB∥CD( ___________,两直线平行).
还有方法三吗?
125
∠2=125°
∠DNM
∠2
内错角相等
14.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,求证:BE∥AC.
辨析应用
解:∵BE平分∠ABD,∴_________=__________;∵∠ABE=∠C,∴_________=_________,(等量代换)∴BE∥AC( ___________,两直线平行).
你有几种方法可以解决呢?
还有别的方法吗?
∠ABE
∠DBE
∠DBE
∠C
同位角相等
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
六年级下册数学精品课件
《探索直线平行的条件》
在一个平面内,有三条直线,则交点的个数
可能是_______________
0或1或2或3
角……来了!
三线八角:
如图,你有几种方法,可以说明a∥b呢?
请用如下的方式写写看:
因为∠_______=∠______
所以a∥b
……
共有多少种方法呢?
同位角:∠1=∠2,∠3=∠4, ∠5=∠6,∠7=∠8
内错角:∠7=∠2,∠5=∠4
同旁内角:∠7+∠4=180°, ∠5+∠4=180°
辨析应用
1.
如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6+∠4=180°;其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
D
2.如图,在四边形ABCD中,连结BD,判定正确的是( )
A.若∠1=∠2,则AB∥CD B.若∠3=∠4,则AD∥BC C.若∠A+∠ABC=180°,则AD∥BC D.若∠C=∠A,则AB∥CD
辨析应用
C
3.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠BAC=∠EBD
C.∠ABC=∠BAE
D.∠BAC=∠ABE
辨析应用
D
4.如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是( )
A
B
C
D
辨析应用
D
5.一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135° C.30°和45° D.以上都有可能
辨析应用
当AC∥DE时,
∠BAD=∠DAE=45
当BC∥AD时,
∠DAE=∠B=60 ;
当BC∥AE时,
∵∠EAB=∠B=60 ,
∴∠BAD=∠DAE+∠EAB=105
当AB∥DE时,
∵∠E=∠EAB=90 ,
∴∠BAD=∠DAE+∠EAB=135 .
5.一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135° C.30°和45° D.以上都有可能
辨析应用
B
6.判断题(正确的画“√”,错误的画“×”)(1)a、b、c是直线,且a∥b,b∥c,则a∥c.
(2)a、b、c是直线,且a⊥b,b⊥c,则a⊥c.
辨析应用
√ 平行于同一条直线的两条直线互相平行
垂直于同一条直线的两条直线互相平行 ×
同一平面内
7.如图,直线a、b被直线c所截,∠2=56°,则当∠1=____ 时,a∥b.
8.如图,如果希望直线c∥d,那么需要添加的条件是: .
辨析应用
124°
∠1=∠2
或∠3=∠4
9.如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转 .
辨析应用
8°
10.如图,a,b,c三根木棒钉在一起,∠1=70°,∠2=100°,现将木棒a、b同时顺时针旋转一周,速度分别为17度/秒和2度/秒,则 秒后木棒a,b平行.
辨析应用
解:设t秒后木棒a,b平行,依题意有100°﹣17°t=70°﹣2°t, 解得t=2.
所以2秒后木棒a,b平行.
11.如图,直线a,点B,点C.(1)过点B画直线a的平行线,能画几条?(2)过点C画直线a的平行线,它与过点B的平行线平行吗?
辨析应用
12.如图,∠ACB=90°,∠A=35°,∠BCD=55°.
试说明:AB∥CD.
辨析应用
解:∵∠ACB=90°,
∠A=35°,∴∠B=_____°,∵∠BCD=55°,∴_____=__________,∴CD∥AB( __________ , 两直线平行 )
55
∠B
∠BCD
内错角相等
13.如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
辨析应用
方法一
证明:∵∠1=55°(已知),∴∠CNM=______°(对顶角相等),∵ ________(已知),∴_________+______=180°(等式的性质),∴AB∥CD(同旁内角互补,两直线平行).
55
∠2=125°
∠CNM
∠2
13.
如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
辨析应用
方法二
证明:∵∠1=55°(已知),∴∠DNM=______°(邻补角的定义),∵ ____________(已知),∴____________=______(等式的性质),∴AB∥CD( ___________,两直线平行).
还有方法三吗?
125
∠2=125°
∠DNM
∠2
内错角相等
14.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,求证:BE∥AC.
辨析应用
解:∵BE平分∠ABD,∴_________=__________;∵∠ABE=∠C,∴_________=_________,(等量代换)∴BE∥AC( ___________,两直线平行).
你有几种方法可以解决呢?
还有别的方法吗?
∠ABE
∠DBE
∠DBE
∠C
同位角相等
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
