7.3平行线的性质(第2课时) 课件(共19张PPT)
文档属性
| 名称 | 7.3平行线的性质(第2课时) 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 20:31:53 | ||
图片预览



文档简介
(共19张PPT)
2022年春鲁教版数学
六年级下册数学精品课件
第二课时
《平行线的性质》
问题1:平行线的性质有哪几条?
温故知新
问题2:判别直线平行的条件有哪几个?
你现在一共有几个判定直线平行
的方法?
问题3:在应用二者时应注意什么问题?
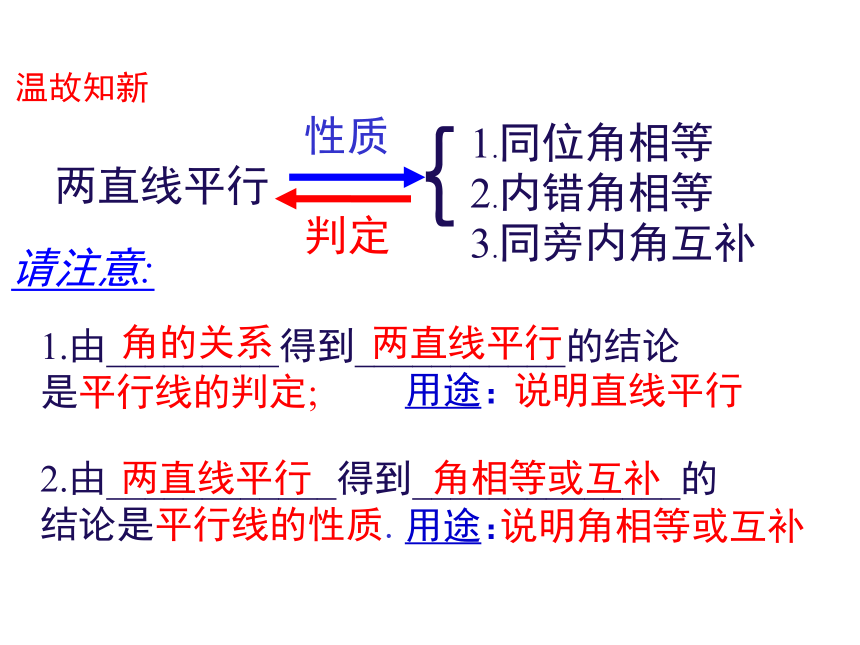
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
说明直线平行
两直线平行
角相等或互补
说明角相等或互补
温故知新
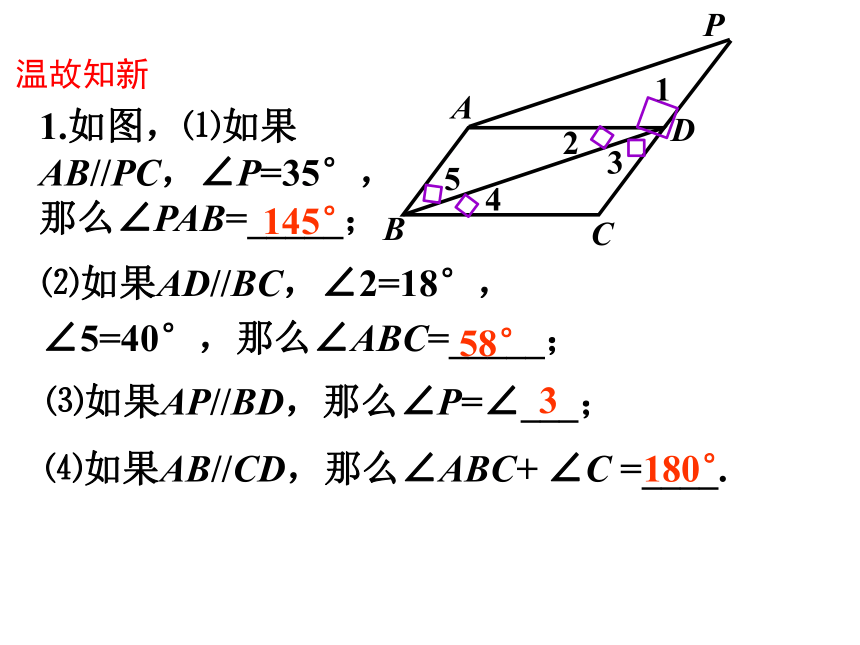
1.如图,⑴如果AB//PC,∠P=35°,那么∠PAB=_____;
145°
58°
3
180°
⑵如果AD//BC,∠2=18°,
∠5=40°,那么∠ABC=_____;
⑶如果AP//BD,那么∠P=∠___;
⑷如果AB//CD,那么∠ABC+ ∠C =____.
C
B
A
D
P
4
5
2
3
1
温故知新
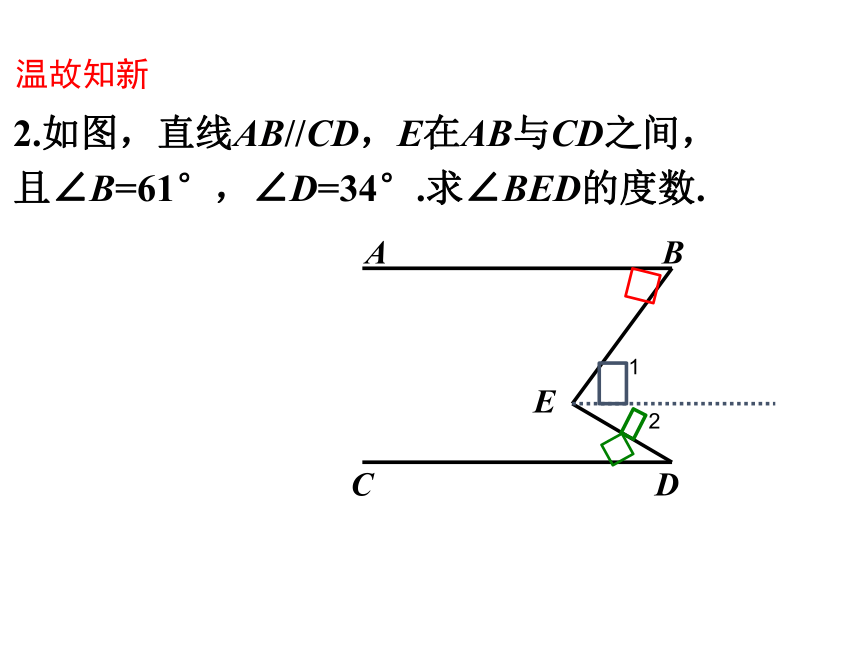
2.如图,直线AB//CD,E在AB与CD之间,
且∠B=61°,∠D=34°.求∠BED的度数.
A
B
E
D
C
1
2
温故知新
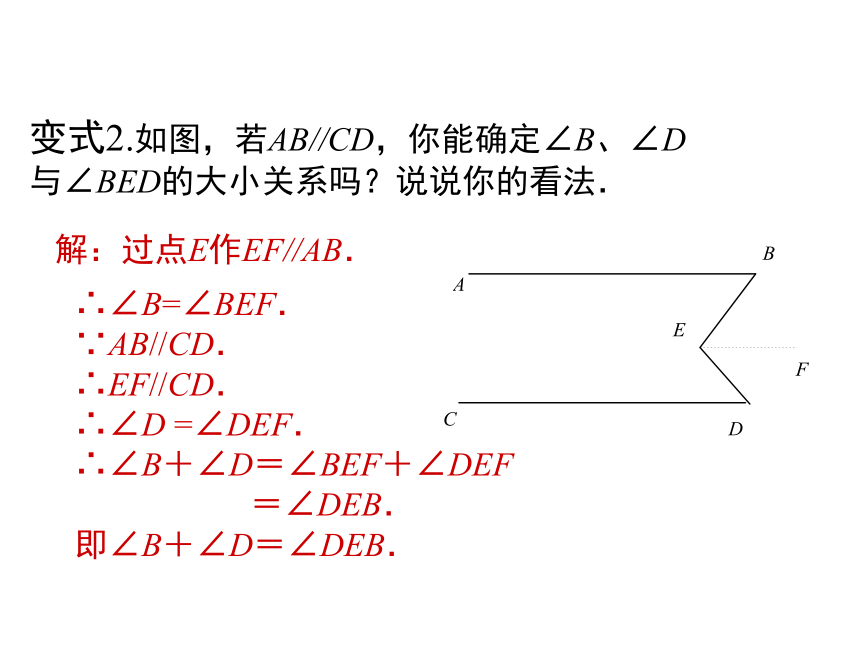
变式2.如图,若AB//CD,你能确定∠B、∠D与∠BED的大小关系吗?说说你的看法.
解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB.
例1 如图:(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
探究新知
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
例2 如图 ,AB∥CD,如果∠1=∠2,
那么EF与AB 平行吗?说说你的理由.
解:EF与AB平行.
探究新知
因为 ∠1 = ∠2,
根据“内错角相等,两直线平行”,
所以 EF∥CD.
又因为 AB∥CD,
根据“平行于同一条直线的两条直线平行”
所以 EF∥AB.
例3 如图,已知直线a∥b,直线c∥d,∠1=107°,求∠2,∠3 的度数.
解:因为a∥b,
根据“两直线平行,内错角相等”
所以 ∠2 = ∠1 = 107° .
探究新知
因为 c∥d,
根据“两直线平行,同旁内角互补” ,
所以 ∠1 + ∠3 = 180° ,
所以 ∠3 = 180°- ∠1 = 180°-107° = 73° .
想一想
如图,直线a,b被直线c所截,
(1)当∠2=∠4时, 直线a∥b吗?
说出你的理由.
4
(2)当∠2=∠4时, ∠1=∠2吗?
∠2+∠3=180°吗? 说出
你的理由.
巩固练习
2.如图,AE∥CD,若∠1=37°,∠D =54°,求∠2 和∠BAE的度数.
1.如图,∠1 = 105°,∠2 =75°,
你能判断a∥b吗?
3.如图,选择合适的内容填空.
(1)因为AB//CD
所以∠1=∠2
( )
(2)因为∠3=∠1
所以 //__(同位角相等,两直线平行)
(3)因为∠1+∠ =180 ,
所以AB//CD( )
两直线平行,内错角相等
AB CD
4
同旁内角互补,两直线平行
巩固练习
拓展提高
1.如图,平行直线AB,CD被直线EF所截,分别交直线AB,CD于点G,M。GH和MN分别是∠EGB和∠EMD的角平分线。
问:直线GH和MN平行吗?请说明理由。
2.如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.
求证:∠1+∠2=90°.
1
2
A
B
C
D
E
E
拓展提高
3.小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
D
C
E
F
A
A
G
G
1
2
拓展提高
1、本节课主要应用了哪些知识?
2、在应用它们时,你认为应该注意哪些问题?
3、在写几何推理的过程中,因为和所以分
别表达的意义是什么?根据是什么?
课堂小结
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
六年级下册数学精品课件
第二课时
《平行线的性质》
问题1:平行线的性质有哪几条?
温故知新
问题2:判别直线平行的条件有哪几个?
你现在一共有几个判定直线平行
的方法?
问题3:在应用二者时应注意什么问题?
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
说明直线平行
两直线平行
角相等或互补
说明角相等或互补
温故知新
1.如图,⑴如果AB//PC,∠P=35°,那么∠PAB=_____;
145°
58°
3
180°
⑵如果AD//BC,∠2=18°,
∠5=40°,那么∠ABC=_____;
⑶如果AP//BD,那么∠P=∠___;
⑷如果AB//CD,那么∠ABC+ ∠C =____.
C
B
A
D
P
4
5
2
3
1
温故知新
2.如图,直线AB//CD,E在AB与CD之间,
且∠B=61°,∠D=34°.求∠BED的度数.
A
B
E
D
C
1
2
温故知新
变式2.如图,若AB//CD,你能确定∠B、∠D与∠BED的大小关系吗?说说你的看法.
解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB.
例1 如图:(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
探究新知
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
例2 如图 ,AB∥CD,如果∠1=∠2,
那么EF与AB 平行吗?说说你的理由.
解:EF与AB平行.
探究新知
因为 ∠1 = ∠2,
根据“内错角相等,两直线平行”,
所以 EF∥CD.
又因为 AB∥CD,
根据“平行于同一条直线的两条直线平行”
所以 EF∥AB.
例3 如图,已知直线a∥b,直线c∥d,∠1=107°,求∠2,∠3 的度数.
解:因为a∥b,
根据“两直线平行,内错角相等”
所以 ∠2 = ∠1 = 107° .
探究新知
因为 c∥d,
根据“两直线平行,同旁内角互补” ,
所以 ∠1 + ∠3 = 180° ,
所以 ∠3 = 180°- ∠1 = 180°-107° = 73° .
想一想
如图,直线a,b被直线c所截,
(1)当∠2=∠4时, 直线a∥b吗?
说出你的理由.
4
(2)当∠2=∠4时, ∠1=∠2吗?
∠2+∠3=180°吗? 说出
你的理由.
巩固练习
2.如图,AE∥CD,若∠1=37°,∠D =54°,求∠2 和∠BAE的度数.
1.如图,∠1 = 105°,∠2 =75°,
你能判断a∥b吗?
3.如图,选择合适的内容填空.
(1)因为AB//CD
所以∠1=∠2
( )
(2)因为∠3=∠1
所以 //__(同位角相等,两直线平行)
(3)因为∠1+∠ =180 ,
所以AB//CD( )
两直线平行,内错角相等
AB CD
4
同旁内角互补,两直线平行
巩固练习
拓展提高
1.如图,平行直线AB,CD被直线EF所截,分别交直线AB,CD于点G,M。GH和MN分别是∠EGB和∠EMD的角平分线。
问:直线GH和MN平行吗?请说明理由。
2.如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.
求证:∠1+∠2=90°.
1
2
A
B
C
D
E
E
拓展提高
3.小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
D
C
E
F
A
A
G
G
1
2
拓展提高
1、本节课主要应用了哪些知识?
2、在应用它们时,你认为应该注意哪些问题?
3、在写几何推理的过程中,因为和所以分
别表达的意义是什么?根据是什么?
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
