7.4用尺规作角 课件(共19张PPT)
文档属性
| 名称 | 7.4用尺规作角 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-09 20:55:21 | ||
图片预览





文档简介
(共19张PPT)
2022年春鲁教版数学
六年级下册数学精品课件
《用尺规作角》
1.只用没有 的直尺和 作图成为尺规作图。
2.尺规作图时,直尺的功能是
3.圆规的功能是
刻度
圆规
连接两点之间的线段、过两点画直线和射线
画圆或弧、截取一条线段等于已知线段
1.作一条线段等于已知线段
利用直尺和圆规可以作出很多几何图形,
还记得我们是如何用圆规和直尺作一条线段
等于已知线段的吗?
已知:线段AB.
求作:线段A’ B’,使A’ B’=AB.
A
B
1作射线A’C’
A’ C’
2以点A’为圆心,
以AB的长为半径
画弧,
交射线A’ C’于点B’,
B’
A’
A’B’ 就是所求作的线段。
示 范
作 法
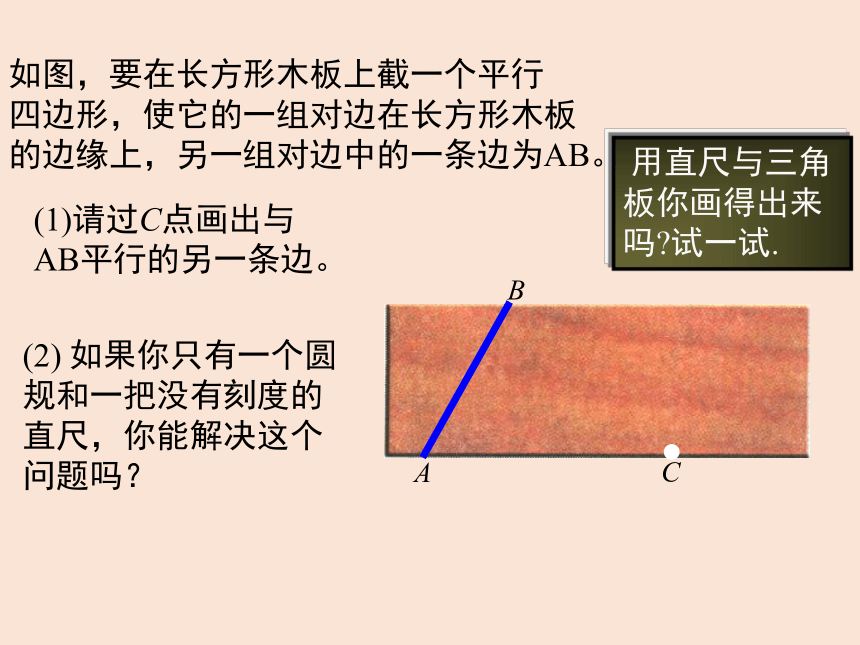
如图,要在长方形木板上截一个平行
四边形,使它的一组对边在长方形木板
的边缘上,另一组对边中的一条边为AB。
A
B
C
请过C点画出与
AB平行的另一条边。
(2) 如果你只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?
用直尺与三角板你画得出来吗 试一试.
A
B
D
C
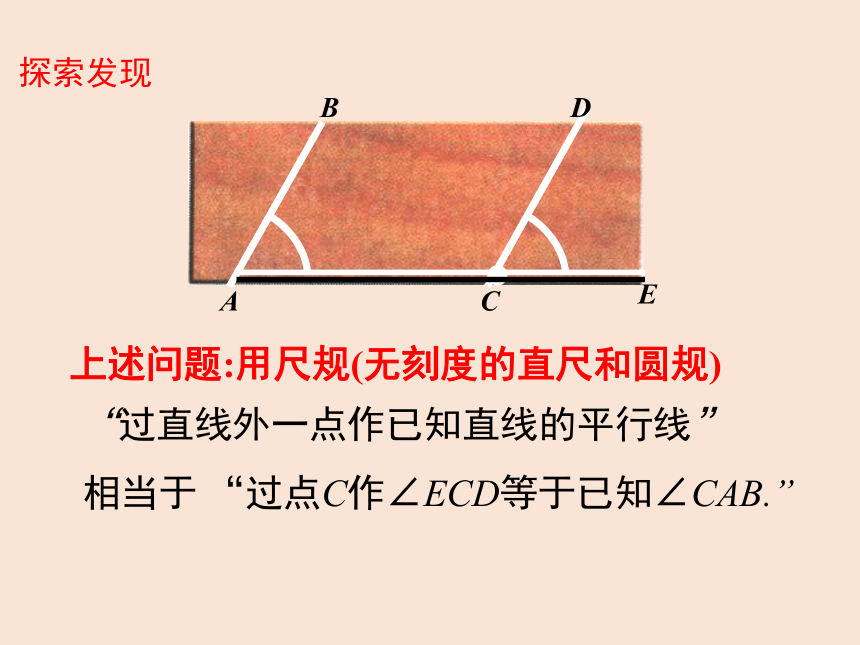
上述问题:用尺规(无刻度的直尺和圆规)
“过直线外一点作已知直线的平行线”
相当于 “过点C作∠ECD等于已知∠CAB.”
E
探索发现
B
O
A
O’
A’
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O’为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C’
(4) 以点C’为圆心,
CD长为半径
画弧,
D’
(5) 过点D’作射线O’B’.
B’
∠A’O’B’就是所求的角.
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
已知: ∠AOB 求作: ∠A’O’B’ 使∠A’O’B’=∠AOB
2.作一个角等于已知角
请用没有刻度的直尺和圆规, 在课本的图中, 过点C作AB的平行线.
A
B
C
分析:若以点C为顶点作一个角∠FCE
与∠BAC 相等,
则∠FCE的边CF
所在的直线即为所求.
E
G
G’
H
D
F
随堂练习
议一议
O’
E
F
A
O
B
已知: ∠AOB.
利用尺规作: ∠A’O’B’
使∠A’O’B’=2∠AOB。
B
O
A
独立思考、合作交流;
口述作法、保留作图痕迹.
作法一:
C
A’
B’
∠A’OB’即为所求作的角.
B
O
A
法二:
C
D
C’
E
B’
O’
A’
∠A’O’B’即为所求作的角
随堂练习
已知: ∠1, ∠2
求作: ∠AOB,使得∠AOB= ∠1+∠2
1
2
你会作两个角的和了吗?
随堂练习
已知: ∠1, ∠2
求作: ∠AOB,使得∠AOB= ∠1-∠2
1
2
你会作两个角的差了吗?
随堂练习
如图,已知∠ABC,请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边于点P.
探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.
画图如图①②③④所示
解:
如图①,∵AB∥DE,
∴∠ABC=∠DPC.
∵BC∥EF,
∴∠DEF=∠DPC.
∴∠ABC=∠DEF.
如图②,∵AB∥DE,
∴∠ABC=∠EPC.
∵BC∥EF,
∴∠EPC=∠DEF.
∴∠ABC=∠DEF.
如图③,∵AB∥DE,
∴∠ABC=∠BPE.
∵BC∥EF,
∴∠DEF+∠BPE=180°.
∴∠ABC+∠DEF=180°.
如图④,∵AB∥DE,
∴∠ABC=∠EPC.
∵BC∥EF,
∴∠EPC+∠DEF=180°.
∴∠ABC+∠DEF=180°.
综上可知,∠ABC与∠DEF相等或互补.
1.尺规作一个角等于已知角
课堂小结
2.数学语言——文字语言与图形语言的转换
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
六年级下册数学精品课件
《用尺规作角》
1.只用没有 的直尺和 作图成为尺规作图。
2.尺规作图时,直尺的功能是
3.圆规的功能是
刻度
圆规
连接两点之间的线段、过两点画直线和射线
画圆或弧、截取一条线段等于已知线段
1.作一条线段等于已知线段
利用直尺和圆规可以作出很多几何图形,
还记得我们是如何用圆规和直尺作一条线段
等于已知线段的吗?
已知:线段AB.
求作:线段A’ B’,使A’ B’=AB.
A
B
1作射线A’C’
A’ C’
2以点A’为圆心,
以AB的长为半径
画弧,
交射线A’ C’于点B’,
B’
A’
A’B’ 就是所求作的线段。
示 范
作 法
如图,要在长方形木板上截一个平行
四边形,使它的一组对边在长方形木板
的边缘上,另一组对边中的一条边为AB。
A
B
C
请过C点画出与
AB平行的另一条边。
(2) 如果你只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?
用直尺与三角板你画得出来吗 试一试.
A
B
D
C
上述问题:用尺规(无刻度的直尺和圆规)
“过直线外一点作已知直线的平行线”
相当于 “过点C作∠ECD等于已知∠CAB.”
E
探索发现
B
O
A
O’
A’
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O’为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C’
(4) 以点C’为圆心,
CD长为半径
画弧,
D’
(5) 过点D’作射线O’B’.
B’
∠A’O’B’就是所求的角.
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
已知: ∠AOB 求作: ∠A’O’B’ 使∠A’O’B’=∠AOB
2.作一个角等于已知角
请用没有刻度的直尺和圆规, 在课本的图中, 过点C作AB的平行线.
A
B
C
分析:若以点C为顶点作一个角∠FCE
与∠BAC 相等,
则∠FCE的边CF
所在的直线即为所求.
E
G
G’
H
D
F
随堂练习
议一议
O’
E
F
A
O
B
已知: ∠AOB.
利用尺规作: ∠A’O’B’
使∠A’O’B’=2∠AOB。
B
O
A
独立思考、合作交流;
口述作法、保留作图痕迹.
作法一:
C
A’
B’
∠A’OB’即为所求作的角.
B
O
A
法二:
C
D
C’
E
B’
O’
A’
∠A’O’B’即为所求作的角
随堂练习
已知: ∠1, ∠2
求作: ∠AOB,使得∠AOB= ∠1+∠2
1
2
你会作两个角的和了吗?
随堂练习
已知: ∠1, ∠2
求作: ∠AOB,使得∠AOB= ∠1-∠2
1
2
你会作两个角的差了吗?
随堂练习
如图,已知∠ABC,请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边于点P.
探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.
画图如图①②③④所示
解:
如图①,∵AB∥DE,
∴∠ABC=∠DPC.
∵BC∥EF,
∴∠DEF=∠DPC.
∴∠ABC=∠DEF.
如图②,∵AB∥DE,
∴∠ABC=∠EPC.
∵BC∥EF,
∴∠EPC=∠DEF.
∴∠ABC=∠DEF.
如图③,∵AB∥DE,
∴∠ABC=∠BPE.
∵BC∥EF,
∴∠DEF+∠BPE=180°.
∴∠ABC+∠DEF=180°.
如图④,∵AB∥DE,
∴∠ABC=∠EPC.
∵BC∥EF,
∴∠EPC+∠DEF=180°.
∴∠ABC+∠DEF=180°.
综上可知,∠ABC与∠DEF相等或互补.
1.尺规作一个角等于已知角
课堂小结
2.数学语言——文字语言与图形语言的转换
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
