2022年鲁教版数学七年级下册 10.2 等腰三角形 第3课时 课件(21张)
文档属性
| 名称 | 2022年鲁教版数学七年级下册 10.2 等腰三角形 第3课时 课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
2 等腰三角形(第3课时)
1、学会证明等角对等边,并进行等腰三角形的判定;
2、体会反证法,并会用反证法进行证明;
3、规范证明的书写过程.
请同学们回答下面的问题:
1、等腰三角形的性质是什么?
①有两个相等的角.
②有两条相等的边.
③底边上的中线、高和顶角的平分线重合.
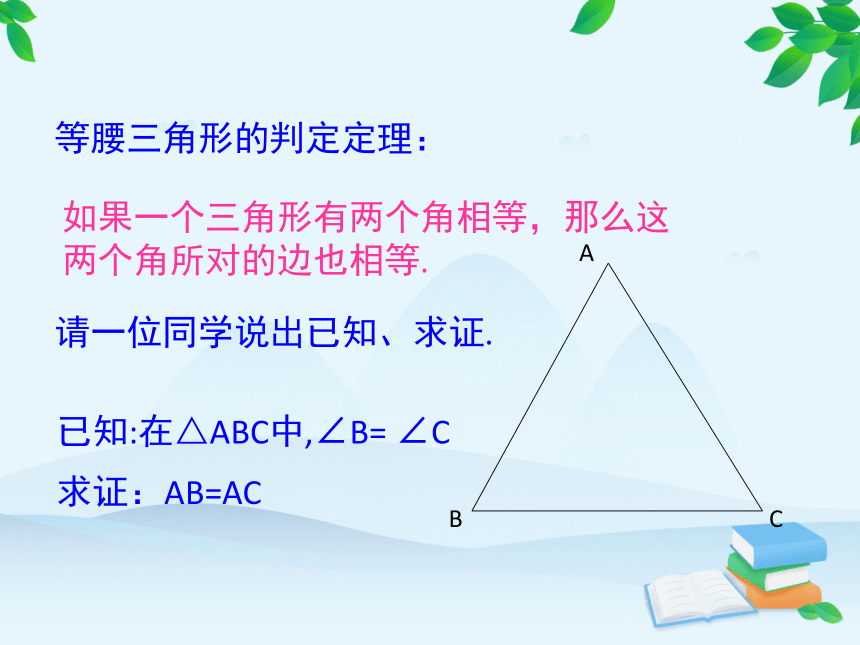
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等.
请一位同学说出已知、求证.
已知:在△ABC中,∠B= ∠C
求证:AB=AC
A
B
C
A
B
C
D
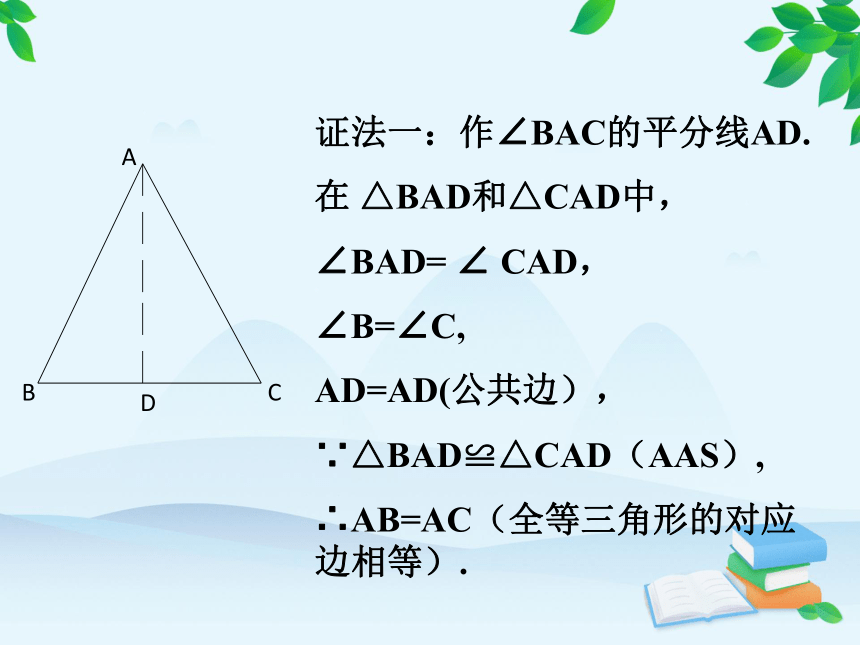
证法一:作∠BAC的平分线AD.
在 △BAD和△CAD中,
∠BAD= ∠ CAD,
∠B=∠C,
AD=AD(公共边),
∵△BAD≌△CAD(AAS),
∴AB=AC(全等三角形的对应边相等).
A
B
C
D
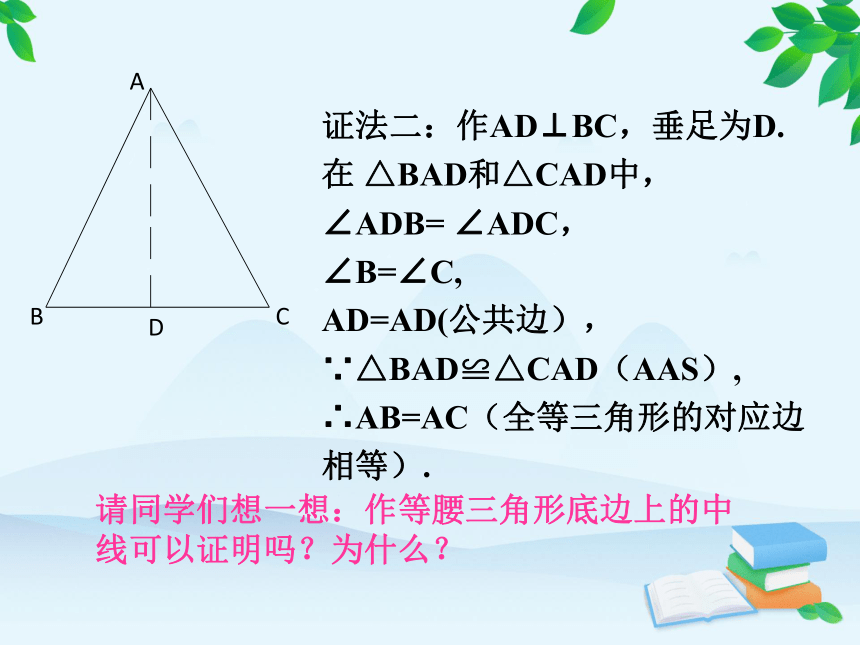
证法二:作AD⊥BC,垂足为D.
在 △BAD和△CAD中,
∠ADB= ∠ADC,
∠B=∠C,
AD=AD(公共边),
∵△BAD≌△CAD(AAS),
∴AB=AC(全等三角形的对应边相等).
请同学们想一想:作等腰三角形底边上的中线可以证明吗?为什么?
A
B
C
D
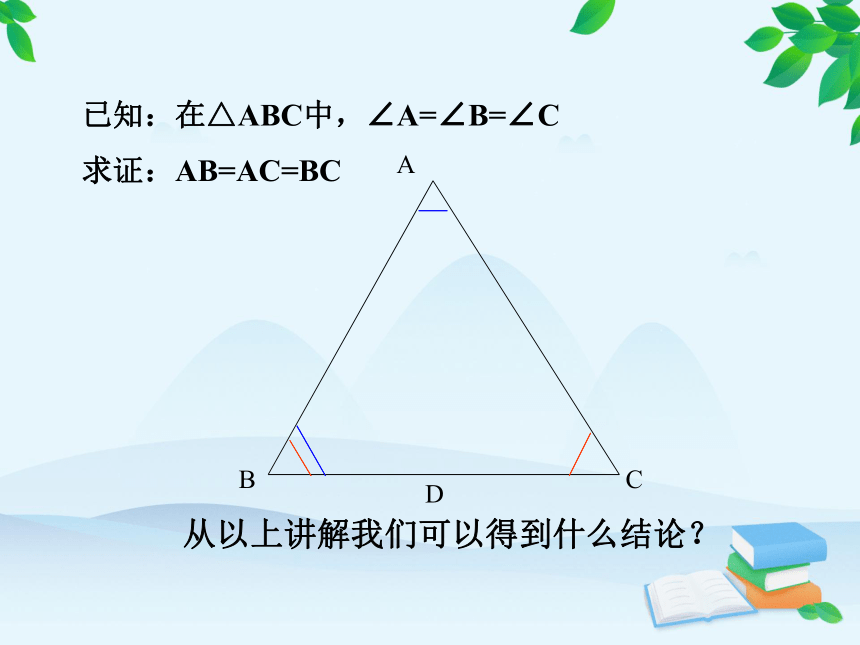
从以上讲解我们可以得到什么结论?
已知:在△ABC中,∠A=∠B=∠C
求证:AB=AC=BC
这是由判定定理推导出的一个定理,即判定一个三角形是等边三角形的一种方法.
推论1:三个角都相等的三角形是等边三角形.
A
B
C
D
60°
60°
你又可以得到什么?
已知:在等腰△ABC中,AB=AC,∠A=60°(或者∠B=60°)
求证:AB=AC=BC
推论2:有一个角等于60°的等腰三角形是等边三角形.
这是由判定定理推导出的又一个定理,即判定一个三角形是等边三角形的另外一种方法.
小明说,在一个三角形中,如果两个角不相等,
那么这两个角所对的边也不相等.
即
C
A
B
在△ABC中, 如果∠B≠∠C,
那么AB≠AC.
你认为这个结论成立吗
如果成立,你能证明它吗
小明是这样想的:
如图,在△ABC中,已知∠B≠∠C,
此时,AB与AC要么相等,要么不相等.
假设AB=AC, 那么根据“等边对等角”定理可得∠B=∠C,
但已知条件是 ∠B≠∠C.
“∠B=∠C”与“∠B≠∠C”相矛盾,
因此, AB≠AC.
论证的新方法----反证法
小明在证明时,先假设命题的结论不成立,然后推导出与定义、基本事实、公理、已证定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.
这种证明方法称为反证法(reduction to absurdity)
假设AB=AC, 那么根据“等边对等角”
定理可得∠B=∠C .
但已知条件是∠B≠∠C.
“∠B=∠C”与“∠B≠∠C”相矛盾,
因此,AB≠AC.
反证法是一种重要的数学证明方法.
在解决某些问题时常常会有出人意料的作用.
C
A
B
求证: 一个三角形中不能有两个角是直角。
(用反证法来证)
证明:
假设△ABC中有两个直角 ,不妨设∠A=∠B=90° ,
那么∠A+∠B+∠C=180°+∠C>180°,
这与三角形的内角和定理相矛盾
∴假设不成立
∴△ABC中不能有两个直角
已知:△ABC
求证: ∠A、 ∠ B、∠C中不能有两个角是直角
求证: 如果a1,a2,a3,a4,a5都是正数,且a1+a2+a3+a4+a5=1,
那么,这五个数中至少有一个大于或等于1/5.
假设这五个数中没有一个大于或等于1/5,
即都得小于1/5,
那么这五个数的和a1+a2+a3+a4+a5就小于1.
这与已知这五个数的和a1+a2+a3+a4+a5=1相矛盾.
因此,这五个数中至少有一个大于或等于1/5.
(用反证法来证)
证明:
例1 如图,已知∠A=36°,∠DBC=36°,∠C=72°,计算∠1和∠2的度数,并说明图中有哪些等腰三角形.
A
B
C
D
36°
36°
2
1
72°
解:∵∠A=36°∠DBC= 36° ∠C= 72°
∴∠2=180 °- ∠A - ∠DBC - ∠C = 36°
(三角形内角和定理)
∴ ∠A= ∠2
∴AD=BD(等角对等边)
∵ ∠1= ∠A +∠2= 72°= ∠C
∴BD=BC (等角对等边)
∴图中的等腰三角形有△ADB、△ABC、△BDC三个.
例2 如图,CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形。
C
A
D
B
答:图中的等腰直角三角形有:
等腰Rt△ABC、等腰Rt△ADC和
等腰Rt△ CDB
A
B
C
等腰三角形顶角的平分线、底边上的中线、底边上的高 互相重合。
等腰三角形的两个底角相等.
简称:
等边对等角.
顶角
A
B
C
底边
腰
腰
底角
底角
【定义】
【性质定理】
【性质定理的推论】
有两边相等的三角形叫做等腰三角形;
D
高
(简称:“三线合一”)
【判定定理】
有两个角相等的三角形是等腰三角形.
简称:
等角对等边.
等腰三角形:
底角的两条平分线相等;
两条腰上的中线相等;
两条腰上的高线相等。
A
C
B
D
●
●
E
●●
●●
A
C
B
M
N
A
C
B
P
Q
等边三角形(特殊的等腰三角形)
等边三角形的三个内角都相等,
并且每个角都等于60°。
【定义】
【性质定理】
有三边相等的三角形叫做等边三角形;
用反证法证题的一般步骤
1. 假设命题的结论不成立;
2. 从这个假设出发,应用正确的推理方法, 得出与定义、基本事实、已有定理或已知条件 相矛盾的结果;
3. 由矛盾的结果判定假设不正确,从而肯定命题的结论正确.
2 等腰三角形(第3课时)
1、学会证明等角对等边,并进行等腰三角形的判定;
2、体会反证法,并会用反证法进行证明;
3、规范证明的书写过程.
请同学们回答下面的问题:
1、等腰三角形的性质是什么?
①有两个相等的角.
②有两条相等的边.
③底边上的中线、高和顶角的平分线重合.
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等.
请一位同学说出已知、求证.
已知:在△ABC中,∠B= ∠C
求证:AB=AC
A
B
C
A
B
C
D
证法一:作∠BAC的平分线AD.
在 △BAD和△CAD中,
∠BAD= ∠ CAD,
∠B=∠C,
AD=AD(公共边),
∵△BAD≌△CAD(AAS),
∴AB=AC(全等三角形的对应边相等).
A
B
C
D
证法二:作AD⊥BC,垂足为D.
在 △BAD和△CAD中,
∠ADB= ∠ADC,
∠B=∠C,
AD=AD(公共边),
∵△BAD≌△CAD(AAS),
∴AB=AC(全等三角形的对应边相等).
请同学们想一想:作等腰三角形底边上的中线可以证明吗?为什么?
A
B
C
D
从以上讲解我们可以得到什么结论?
已知:在△ABC中,∠A=∠B=∠C
求证:AB=AC=BC
这是由判定定理推导出的一个定理,即判定一个三角形是等边三角形的一种方法.
推论1:三个角都相等的三角形是等边三角形.
A
B
C
D
60°
60°
你又可以得到什么?
已知:在等腰△ABC中,AB=AC,∠A=60°(或者∠B=60°)
求证:AB=AC=BC
推论2:有一个角等于60°的等腰三角形是等边三角形.
这是由判定定理推导出的又一个定理,即判定一个三角形是等边三角形的另外一种方法.
小明说,在一个三角形中,如果两个角不相等,
那么这两个角所对的边也不相等.
即
C
A
B
在△ABC中, 如果∠B≠∠C,
那么AB≠AC.
你认为这个结论成立吗
如果成立,你能证明它吗
小明是这样想的:
如图,在△ABC中,已知∠B≠∠C,
此时,AB与AC要么相等,要么不相等.
假设AB=AC, 那么根据“等边对等角”定理可得∠B=∠C,
但已知条件是 ∠B≠∠C.
“∠B=∠C”与“∠B≠∠C”相矛盾,
因此, AB≠AC.
论证的新方法----反证法
小明在证明时,先假设命题的结论不成立,然后推导出与定义、基本事实、公理、已证定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.
这种证明方法称为反证法(reduction to absurdity)
假设AB=AC, 那么根据“等边对等角”
定理可得∠B=∠C .
但已知条件是∠B≠∠C.
“∠B=∠C”与“∠B≠∠C”相矛盾,
因此,AB≠AC.
反证法是一种重要的数学证明方法.
在解决某些问题时常常会有出人意料的作用.
C
A
B
求证: 一个三角形中不能有两个角是直角。
(用反证法来证)
证明:
假设△ABC中有两个直角 ,不妨设∠A=∠B=90° ,
那么∠A+∠B+∠C=180°+∠C>180°,
这与三角形的内角和定理相矛盾
∴假设不成立
∴△ABC中不能有两个直角
已知:△ABC
求证: ∠A、 ∠ B、∠C中不能有两个角是直角
求证: 如果a1,a2,a3,a4,a5都是正数,且a1+a2+a3+a4+a5=1,
那么,这五个数中至少有一个大于或等于1/5.
假设这五个数中没有一个大于或等于1/5,
即都得小于1/5,
那么这五个数的和a1+a2+a3+a4+a5就小于1.
这与已知这五个数的和a1+a2+a3+a4+a5=1相矛盾.
因此,这五个数中至少有一个大于或等于1/5.
(用反证法来证)
证明:
例1 如图,已知∠A=36°,∠DBC=36°,∠C=72°,计算∠1和∠2的度数,并说明图中有哪些等腰三角形.
A
B
C
D
36°
36°
2
1
72°
解:∵∠A=36°∠DBC= 36° ∠C= 72°
∴∠2=180 °- ∠A - ∠DBC - ∠C = 36°
(三角形内角和定理)
∴ ∠A= ∠2
∴AD=BD(等角对等边)
∵ ∠1= ∠A +∠2= 72°= ∠C
∴BD=BC (等角对等边)
∴图中的等腰三角形有△ADB、△ABC、△BDC三个.
例2 如图,CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形。
C
A
D
B
答:图中的等腰直角三角形有:
等腰Rt△ABC、等腰Rt△ADC和
等腰Rt△ CDB
A
B
C
等腰三角形顶角的平分线、底边上的中线、底边上的高 互相重合。
等腰三角形的两个底角相等.
简称:
等边对等角.
顶角
A
B
C
底边
腰
腰
底角
底角
【定义】
【性质定理】
【性质定理的推论】
有两边相等的三角形叫做等腰三角形;
D
高
(简称:“三线合一”)
【判定定理】
有两个角相等的三角形是等腰三角形.
简称:
等角对等边.
等腰三角形:
底角的两条平分线相等;
两条腰上的中线相等;
两条腰上的高线相等。
A
C
B
D
●
●
E
●●
●●
A
C
B
M
N
A
C
B
P
Q
等边三角形(特殊的等腰三角形)
等边三角形的三个内角都相等,
并且每个角都等于60°。
【定义】
【性质定理】
有三边相等的三角形叫做等边三角形;
用反证法证题的一般步骤
1. 假设命题的结论不成立;
2. 从这个假设出发,应用正确的推理方法, 得出与定义、基本事实、已有定理或已知条件 相矛盾的结果;
3. 由矛盾的结果判定假设不正确,从而肯定命题的结论正确.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
