2022年鲁教版数学七年级下册 11.1 不等关系 课件(16张)
文档属性
| 名称 | 2022年鲁教版数学七年级下册 11.1 不等关系 课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 12:00:30 | ||
图片预览





文档简介
(共16张PPT)
1 不等关系
你还记得小孩玩的翘翘板吗?你想过它的工作原理吗?
其实,翘翘板就是靠不断改变两端的重量对比来工作的.
引入新课
B<A<C
B
A
A
C
引入新课
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,并把它们用到了生活实践当中.
讲授新课
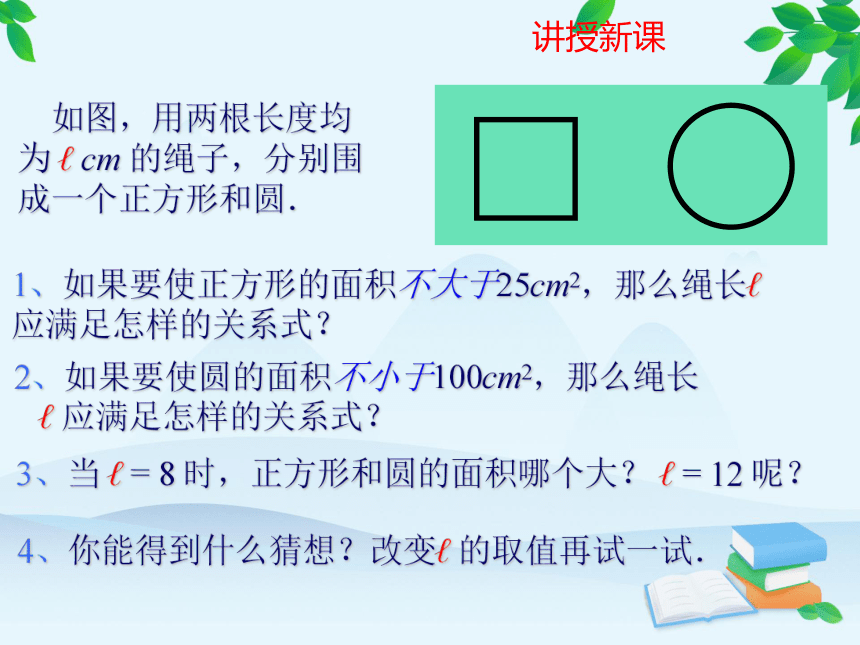
如图,用两根长度均为 cm 的绳子,分别围成一个正方形和圆.
1、如果要使正方形的面积不大于25cm2,那么绳长
应满足怎样的关系式?
2、如果要使圆的面积不小于100cm2,那么绳长
应满足怎样的关系式?
3、当 = 8 时,正方形和圆的面积哪个大? = 12 呢?
4、你能得到什么猜想?改变 的取值再试一试.
讲授新课
1、如果要使正方形的面积不大于25cm2,那么绳长
应满足怎样的关系式?
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为 .
要使正方形的面积不大于25cm2 ,就是 ;
即
≤ 25.
讲授新课
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为 .
≥100
即: .
≥100
2、如果要使圆的面积不小于100cm2,那么绳长
应满足怎样的关系式?
要使圆的面积不小于100cm2,就是
讲授新课
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为
当 = 8 时,正方形的面积为
= 4(cm )
圆的面积为
≈5.1(cm )
∵4< 5.1
∴此时的圆的面积大.
讲授新课
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为
当 = 12时,正方形的面积为
= 9(cm )
圆的面积为
∵9<11.5 ;
≈11.5(cm )
∴此时还是圆的面积大.
.
讲授新课
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为 .
4、你能得到什么猜想?改变 的取值再试一试.
当 = 8、 = 12 时,都是圆的面积大.
我们可以猜想,用长度均为 cm的两根绳子分别围成
一个正方形和圆,无论 取何值,圆的面积总大于正方形的面积, 即
>
讲授新课
观察由上述问题得到的如下关系式,它们有什么共同特点?
(1)
(2)
(3)
(4)
一般地,用符号“<”(或“≤”),“>”(或“≥”)
连接的式子叫做不等式.
≤ 25
≥100
>
5+3x>240
讲授新课
例1 用“<”或“>”号填空:
(1) -7____-5; (2) (-3)4____34;
(3) (-4)2____(-3)2;
(4) |-0.5|____|-1000|;
(5) 3+4____1+4; (6) 5+3____12-5;
(7) 6×3____4×3;(8) 6×(-3)____4×(-3)
<
=
>
<
>
>
>
<
例2 用适当的符号表示下列关系:
(1)a的相反数是正数 ;(2) m与2的差小于 ;
(3) x的与4的和不是正数;
(4) y的一半与x的2倍的和不小于3 .
a<0
x+4≤0
讲授新课
用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a、b都长;
(3)x与17的和比它的5倍小.
c>a
c>b
x+17<5x
a≥0
讲授新课
注:
“不大于”指的是 “ ”;
通常用符号 “ ” 表示.
类似地,“不小于”指的是“等于或大于”.
通常用符号“≥”表示.(读作:“大于或等于”).
等于或小于
≤
例如:x 不大于10 可以表示为
x≤10(读作:“x小于或等于10”) .
不等关系符号
讲授新课
关键词语
表明数量的不等关系
不等号
①大于
②比…大
①小于
②比…小
①不大于
②不超过
③至多
①不小于
②不低于
③至少
≥
>
<
≤
课后小结
文字语言
表明数量的范围特征
符号 语言
a是正数
a是负数
a是非负数
a是非正数
a≤0
a>0
a<0
a≥0
讲授新课
1 不等关系
你还记得小孩玩的翘翘板吗?你想过它的工作原理吗?
其实,翘翘板就是靠不断改变两端的重量对比来工作的.
引入新课
B<A<C
B
A
A
C
引入新课
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,并把它们用到了生活实践当中.
讲授新课
如图,用两根长度均为 cm 的绳子,分别围成一个正方形和圆.
1、如果要使正方形的面积不大于25cm2,那么绳长
应满足怎样的关系式?
2、如果要使圆的面积不小于100cm2,那么绳长
应满足怎样的关系式?
3、当 = 8 时,正方形和圆的面积哪个大? = 12 呢?
4、你能得到什么猜想?改变 的取值再试一试.
讲授新课
1、如果要使正方形的面积不大于25cm2,那么绳长
应满足怎样的关系式?
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为 .
要使正方形的面积不大于25cm2 ,就是 ;
即
≤ 25.
讲授新课
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为 .
≥100
即: .
≥100
2、如果要使圆的面积不小于100cm2,那么绳长
应满足怎样的关系式?
要使圆的面积不小于100cm2,就是
讲授新课
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为
当 = 8 时,正方形的面积为
= 4(cm )
圆的面积为
≈5.1(cm )
∵4< 5.1
∴此时的圆的面积大.
讲授新课
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为
当 = 12时,正方形的面积为
= 9(cm )
圆的面积为
∵9<11.5 ;
≈11.5(cm )
∴此时还是圆的面积大.
.
讲授新课
在上面的问题中,所围成的正方形的面积可以表示
为 ,圆的面积可以表示为 .
4、你能得到什么猜想?改变 的取值再试一试.
当 = 8、 = 12 时,都是圆的面积大.
我们可以猜想,用长度均为 cm的两根绳子分别围成
一个正方形和圆,无论 取何值,圆的面积总大于正方形的面积, 即
>
讲授新课
观察由上述问题得到的如下关系式,它们有什么共同特点?
(1)
(2)
(3)
(4)
一般地,用符号“<”(或“≤”),“>”(或“≥”)
连接的式子叫做不等式.
≤ 25
≥100
>
5+3x>240
讲授新课
例1 用“<”或“>”号填空:
(1) -7____-5; (2) (-3)4____34;
(3) (-4)2____(-3)2;
(4) |-0.5|____|-1000|;
(5) 3+4____1+4; (6) 5+3____12-5;
(7) 6×3____4×3;(8) 6×(-3)____4×(-3)
<
=
>
<
>
>
>
<
例2 用适当的符号表示下列关系:
(1)a的相反数是正数 ;(2) m与2的差小于 ;
(3) x的与4的和不是正数;
(4) y的一半与x的2倍的和不小于3 .
a<0
x+4≤0
讲授新课
用适当的符号表示下列关系:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a、b都长;
(3)x与17的和比它的5倍小.
c>a
c>b
x+17<5x
a≥0
讲授新课
注:
“不大于”指的是 “ ”;
通常用符号 “ ” 表示.
类似地,“不小于”指的是“等于或大于”.
通常用符号“≥”表示.(读作:“大于或等于”).
等于或小于
≤
例如:x 不大于10 可以表示为
x≤10(读作:“x小于或等于10”) .
不等关系符号
讲授新课
关键词语
表明数量的不等关系
不等号
①大于
②比…大
①小于
②比…小
①不大于
②不超过
③至多
①不小于
②不低于
③至少
≥
>
<
≤
课后小结
文字语言
表明数量的范围特征
符号 语言
a是正数
a是负数
a是非负数
a是非正数
a≤0
a>0
a<0
a≥0
讲授新课
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
