人教版 七年级数学下册 6.2.1 立方根 课件 (共17张PPT)
文档属性
| 名称 | 人教版 七年级数学下册 6.2.1 立方根 课件 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 243.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 13:09:17 | ||
图片预览




文档简介
(共17张PPT)
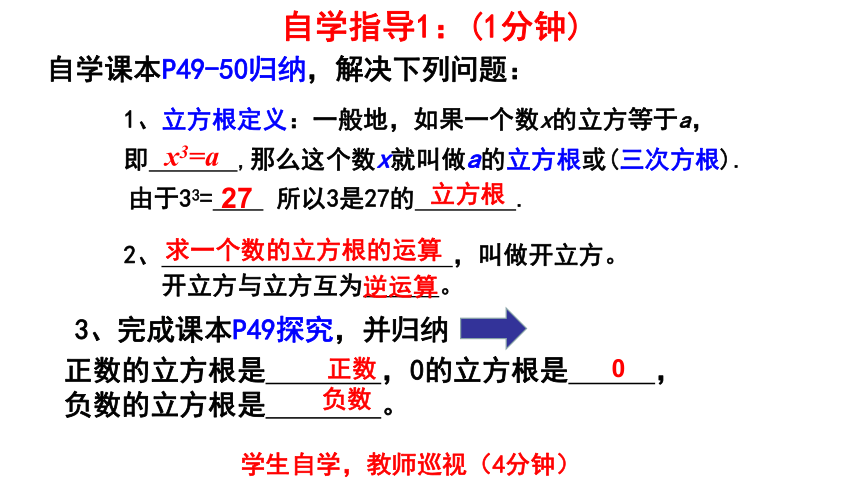
解:设它的棱长为 x cm,根据题意得
x3=27
知识回顾(1分钟)
1、 的平方根是 ,
算术平方根是 。
2、要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?
那么x=?
人教版七年级数学下册
§6.2 立方根
议 课 组:第 一 组
议课时间:2022.3.8
授课时间:2022.3
学习目标(1分钟)
1.立方根的概念及性质,表示一个数的立方根(重点)
2.开立方运算,了解开立方与立方互为逆运算(难点)
3.区分立方根与平方根的不同(易错点)
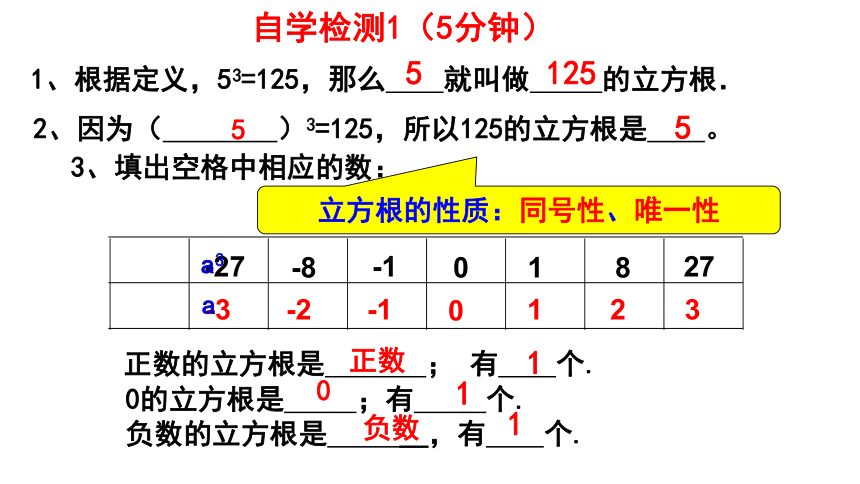
自学指导1:(1分钟)
自学课本P49-50归纳,解决下列问题:
学生自学,教师巡视(4分钟)
1、立方根定义:一般地,如果一个数x的立方等于a,
即 ,那么这个数x就叫做a的立方根或(三次方根).
x3=a
由于33= 所以3是27的 .
27
立方根
正数的立方根是 ,0的立方根是 ,
负数的立方根是 。
正数
0
负数
2、 ,叫做开立方。
开立方与立方互为 。
求一个数的立方根的运算
3、完成课本P49探究,并归纳
逆运算
-27
-8
-1
0
1
8
27
3、填出空格中相应的数:
-3
-2
-1
0
1
2
3
正数的立方根是 ; 有 个.
0的立方根是 ;有 个.
负数的立方根是 __,有 个.
自学检测1(5分钟)
立方根的性质:同号性、唯一性
正数
1
0
1
负数
1
1、根据定义,53=125,那么 就叫做 的立方根.
125
5
a3
a
2、因为( )3=125,所以125的立方根是 。
5
5
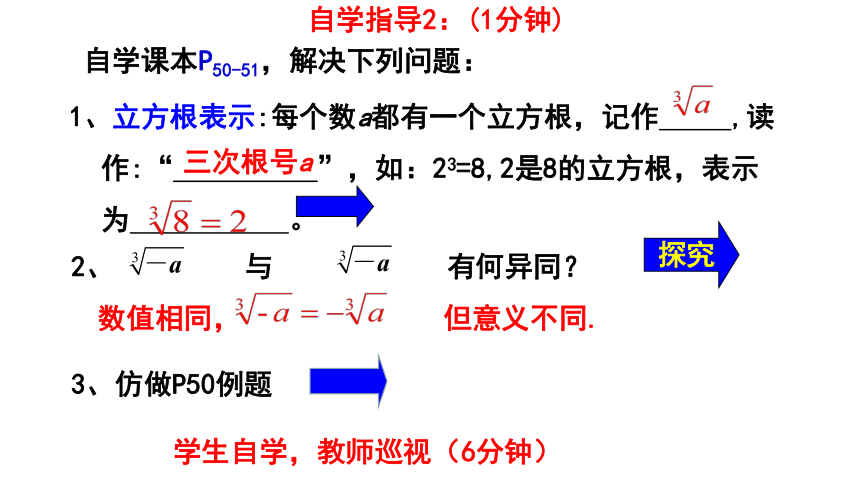
自学指导2:(1分钟)
自学课本P50-51,解决下列问题:
1、立方根表示:每个数a都有一个立方根,记作 ,读作:“ ”,如:23=8,2是8的立方根,表示为 。
学生自学,教师巡视(6分钟)
2、 与 有何异同?
数值相同, 但意义不同.
三次根号a
3、仿做P50例题
探究
2.求下列各数的立方根,找规律。
-8
自学检测2(5分钟)
1. =-27,则-3是-27的________, 表示为 ,
数a的立方根可以表示为 。
立方根
… …
… …
3.根据下列各式结果,归纳被开方数和立方根的规律并填空
0.06
0.6
6
60
归纳:被开方数的小数点每向右(或左)移动三位,
开方后立方根的小数点就向右(或左)移动一位.
8
2
-2
a
a
笔记
笔记
讨论:“平方根”与“立方根”的异同:
平方根 立方根
定义
表示方法
性质
正数:
0:
负数
学生讨论、教师点拨(2分钟)
课堂小结(1分钟)
1、立方根的定义以及立方根的表示方法
注意:表示立方根时,根指数 “3”不能漏写。
2、立方根的性质:
唯一性:一个数只有一个立方根
同号性:立方根的符号与被开方数的符号相同
3、运用开立方解决一些实际问题
注意: ① 运算时注意符号的变化
②被开方数是带分数时,先把它化为
假分数,再进行开方。
1、下列语句正确的是( )
A.27的立方根是±3 B. 的立方根是
C.-2是-8的立方根
D.一个有理数的立方根不是正数就是负数
2、
A. ±8 B.±4 C.2 D.±2
C
D
当堂训练(15分钟):
3、填空:
10
4
9
灵活运用公式:
4、立方根等于它本身的数是 _______
平方根等于它本身的数是 _______ .
算术平方根等于它本身的数_______ .
1、-1、0
0
1、0
5、估计58的立方根的大小在( )
A.2与3之间 B.3与4之间
C.4与5之间 D.5与6之间
正本作业:P52 T3 T5
B
6、
7、
-4
-68800
8、 的平方根和立方根分别是 ( )
A 、
B 、
C、
D、
9、解方程
D
(选做题)
10、 是_____的立方根,
11
3
11
3
3
的立方根是_______.
板书设计
一:立方根的定义及表示方法
二:开立方的定义及性质
求一个数a的立方根的运算叫开立方
6.2立方根
三:立方根的重要结论
立方根具有唯一性和同号性
根据立方根的意义填空.
因为23 =8,所以8的立方根是( )
因为( ) 3 =0.064,所以0.064的立方根是( )
因为( ) 3=0,所以0的立方根是( )
因为( ) 3=-8,所以-8的立方根是( )
0
2
0.4
0.4
-2
0
-2
因为( ) =- ,所以- 的立方根是( )
一般地,如果一个数x的立方等于a,即x3=a,那么
这个数x就叫做a的立方根。
概念分析:
由定义可得2是8的立方根
1.定义:
2.立方根的表示方法:
读作:“三次根号a”
3叫做根指数
注意:根指数3不能省略
a叫做被开方数
探究
因为 =
,
=
所以
因为
=
,
=
所以
猜一猜:
你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?
a
3
-a
3
=
-2
-2
=
-3
-3
互为相反数的数的立方根也互为相反数
=
例:求下列各式的值
(1)
(2)
(3)
解:
(1)
=4
解:设它的棱长为 x cm,根据题意得
x3=27
知识回顾(1分钟)
1、 的平方根是 ,
算术平方根是 。
2、要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?
那么x=?
人教版七年级数学下册
§6.2 立方根
议 课 组:第 一 组
议课时间:2022.3.8
授课时间:2022.3
学习目标(1分钟)
1.立方根的概念及性质,表示一个数的立方根(重点)
2.开立方运算,了解开立方与立方互为逆运算(难点)
3.区分立方根与平方根的不同(易错点)
自学指导1:(1分钟)
自学课本P49-50归纳,解决下列问题:
学生自学,教师巡视(4分钟)
1、立方根定义:一般地,如果一个数x的立方等于a,
即 ,那么这个数x就叫做a的立方根或(三次方根).
x3=a
由于33= 所以3是27的 .
27
立方根
正数的立方根是 ,0的立方根是 ,
负数的立方根是 。
正数
0
负数
2、 ,叫做开立方。
开立方与立方互为 。
求一个数的立方根的运算
3、完成课本P49探究,并归纳
逆运算
-27
-8
-1
0
1
8
27
3、填出空格中相应的数:
-3
-2
-1
0
1
2
3
正数的立方根是 ; 有 个.
0的立方根是 ;有 个.
负数的立方根是 __,有 个.
自学检测1(5分钟)
立方根的性质:同号性、唯一性
正数
1
0
1
负数
1
1、根据定义,53=125,那么 就叫做 的立方根.
125
5
a3
a
2、因为( )3=125,所以125的立方根是 。
5
5
自学指导2:(1分钟)
自学课本P50-51,解决下列问题:
1、立方根表示:每个数a都有一个立方根,记作 ,读作:“ ”,如:23=8,2是8的立方根,表示为 。
学生自学,教师巡视(6分钟)
2、 与 有何异同?
数值相同, 但意义不同.
三次根号a
3、仿做P50例题
探究
2.求下列各数的立方根,找规律。
-8
自学检测2(5分钟)
1. =-27,则-3是-27的________, 表示为 ,
数a的立方根可以表示为 。
立方根
… …
… …
3.根据下列各式结果,归纳被开方数和立方根的规律并填空
0.06
0.6
6
60
归纳:被开方数的小数点每向右(或左)移动三位,
开方后立方根的小数点就向右(或左)移动一位.
8
2
-2
a
a
笔记
笔记
讨论:“平方根”与“立方根”的异同:
平方根 立方根
定义
表示方法
性质
正数:
0:
负数
学生讨论、教师点拨(2分钟)
课堂小结(1分钟)
1、立方根的定义以及立方根的表示方法
注意:表示立方根时,根指数 “3”不能漏写。
2、立方根的性质:
唯一性:一个数只有一个立方根
同号性:立方根的符号与被开方数的符号相同
3、运用开立方解决一些实际问题
注意: ① 运算时注意符号的变化
②被开方数是带分数时,先把它化为
假分数,再进行开方。
1、下列语句正确的是( )
A.27的立方根是±3 B. 的立方根是
C.-2是-8的立方根
D.一个有理数的立方根不是正数就是负数
2、
A. ±8 B.±4 C.2 D.±2
C
D
当堂训练(15分钟):
3、填空:
10
4
9
灵活运用公式:
4、立方根等于它本身的数是 _______
平方根等于它本身的数是 _______ .
算术平方根等于它本身的数_______ .
1、-1、0
0
1、0
5、估计58的立方根的大小在( )
A.2与3之间 B.3与4之间
C.4与5之间 D.5与6之间
正本作业:P52 T3 T5
B
6、
7、
-4
-68800
8、 的平方根和立方根分别是 ( )
A 、
B 、
C、
D、
9、解方程
D
(选做题)
10、 是_____的立方根,
11
3
11
3
3
的立方根是_______.
板书设计
一:立方根的定义及表示方法
二:开立方的定义及性质
求一个数a的立方根的运算叫开立方
6.2立方根
三:立方根的重要结论
立方根具有唯一性和同号性
根据立方根的意义填空.
因为23 =8,所以8的立方根是( )
因为( ) 3 =0.064,所以0.064的立方根是( )
因为( ) 3=0,所以0的立方根是( )
因为( ) 3=-8,所以-8的立方根是( )
0
2
0.4
0.4
-2
0
-2
因为( ) =- ,所以- 的立方根是( )
一般地,如果一个数x的立方等于a,即x3=a,那么
这个数x就叫做a的立方根。
概念分析:
由定义可得2是8的立方根
1.定义:
2.立方根的表示方法:
读作:“三次根号a”
3叫做根指数
注意:根指数3不能省略
a叫做被开方数
探究
因为 =
,
=
所以
因为
=
,
=
所以
猜一猜:
你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?
a
3
-a
3
=
-2
-2
=
-3
-3
互为相反数的数的立方根也互为相反数
=
例:求下列各式的值
(1)
(2)
(3)
解:
(1)
=4
