苏科版数学七年级下册11.6.1一元一次不等式组 课件(共14张PPT)
文档属性
| 名称 | 苏科版数学七年级下册11.6.1一元一次不等式组 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 239.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第十一章 一元一次不等式
11.6一元一次不等式组
课堂小结
例题讲解
归纳总结
随堂演练
情境引入
小丽早晨7时30分骑自行车上学,要在7时50分至7时55分之间到达离家3400m的学校,小丽骑自行车的速度应在什么范围内?
【问题】
(1)如果设小丽骑自行车的速度为x m/min.你可以列出几个不等式?
问题情境一:
(2)如果小丽正好在7点50分到达学校该如何列方程?
如果是在7点50分之后才到达学校又如何列不等式?
20x=3400
20x≤3400
如果小丽要在7点55分之前到校又该如何列不等式?
20x≥3400
①
②
这时有未知数x 同时满足两个不等式,把这两个不等式联立在一起,可以记作 .
像这样,把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组.
归纳总结
下列各式哪些是一元一次不等式组,哪些不是,为什么?
归纳总结
(1)
(3)
(4)
4 ≤3x < 6
4(x+5) >100,
4(y-5)<68;
是
是
不是
不是
【议一议】如何找出使 ① 与② 都成立的未知数x的值?
【问题1】如何在数轴上表示使不等式 成立的未知数x的值?
【问题2】如何在数轴上表示使不等式 成立的未知数x的值?
【问题3】观察所画图形,使不等式 、 都成立的未知数x的值有多少个?
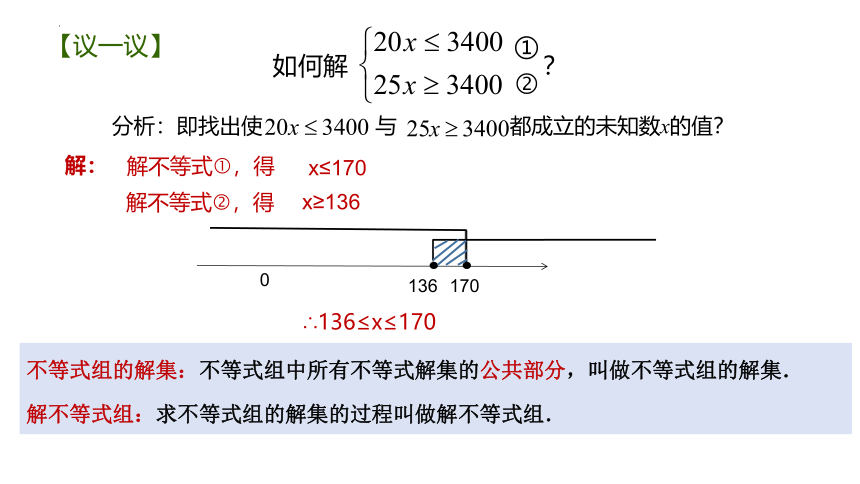
分析:即找出使 与 都成立的未知数x的值?
【议一议】
如何解 ?
①
136
0
170
解不等式 ,得
x≤170
解不等式 ,得
x≥136
∴136≤x≤170
解:
不等式组的解集:不等式组中所有不等式解集的公共部分,叫做不等式组的解集.
解不等式组:求不等式组的解集的过程叫做解不等式组.
例题讲解
求一元一次不等式组解集的
一般步骤:
1、分别求出各个不等式的解集; (求数)
2、利用数轴找出解集的公共部分;(画形)
3、写出不等式组的解集。(写解)
【例题1】利用数轴确定不等式组 的解集.
例题讲解
【练一练】:利用数轴确定下列不等式组的解集.
①不等式组 的解集是 .
②不等式组 的解集是 .
③不等式组 的解集是 .
④不等式组 的解集是 .
课堂练习
x>b
a<x<b
x<a
无解
归纳总结
同大取大
同小取小
大小小大中间找
大大小小找不到
【例题2】利用数轴确定不等式组 的解集.
求一元一次不等式组解集的
一般步骤:
1、分别求出各个不等式的解集; (求数)
2、利用数轴找出解集的公共部分;(画形)
3、写出不等式组的解集。(写解)
【巩固提高】
不等式组 的负整数解是( )
A.-2,0,-1; B.-2;
C.-2,-1; D.不能确定.
C
提高练习
1、关于x的不等式组
有解,那么m的取值范围是( )
A、m>8 B、m≥8 C、m<8D、m≤8
C
2、如果不等式组
的解集是x>a,则a_______b。
≥
课堂小结
通过今天的学习,你学会了什么?
你会正确运用吗?
通过这节课的学习,你有什么感受呢,说出来告诉大家.
第十一章 一元一次不等式
11.6一元一次不等式组
课堂小结
例题讲解
归纳总结
随堂演练
情境引入
小丽早晨7时30分骑自行车上学,要在7时50分至7时55分之间到达离家3400m的学校,小丽骑自行车的速度应在什么范围内?
【问题】
(1)如果设小丽骑自行车的速度为x m/min.你可以列出几个不等式?
问题情境一:
(2)如果小丽正好在7点50分到达学校该如何列方程?
如果是在7点50分之后才到达学校又如何列不等式?
20x=3400
20x≤3400
如果小丽要在7点55分之前到校又该如何列不等式?
20x≥3400
①
②
这时有未知数x 同时满足两个不等式,把这两个不等式联立在一起,可以记作 .
像这样,把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组.
归纳总结
下列各式哪些是一元一次不等式组,哪些不是,为什么?
归纳总结
(1)
(3)
(4)
4 ≤3x < 6
4(x+5) >100,
4(y-5)<68;
是
是
不是
不是
【议一议】如何找出使 ① 与② 都成立的未知数x的值?
【问题1】如何在数轴上表示使不等式 成立的未知数x的值?
【问题2】如何在数轴上表示使不等式 成立的未知数x的值?
【问题3】观察所画图形,使不等式 、 都成立的未知数x的值有多少个?
分析:即找出使 与 都成立的未知数x的值?
【议一议】
如何解 ?
①
136
0
170
解不等式 ,得
x≤170
解不等式 ,得
x≥136
∴136≤x≤170
解:
不等式组的解集:不等式组中所有不等式解集的公共部分,叫做不等式组的解集.
解不等式组:求不等式组的解集的过程叫做解不等式组.
例题讲解
求一元一次不等式组解集的
一般步骤:
1、分别求出各个不等式的解集; (求数)
2、利用数轴找出解集的公共部分;(画形)
3、写出不等式组的解集。(写解)
【例题1】利用数轴确定不等式组 的解集.
例题讲解
【练一练】:利用数轴确定下列不等式组的解集.
①不等式组 的解集是 .
②不等式组 的解集是 .
③不等式组 的解集是 .
④不等式组 的解集是 .
课堂练习
x>b
a<x<b
x<a
无解
归纳总结
同大取大
同小取小
大小小大中间找
大大小小找不到
【例题2】利用数轴确定不等式组 的解集.
求一元一次不等式组解集的
一般步骤:
1、分别求出各个不等式的解集; (求数)
2、利用数轴找出解集的公共部分;(画形)
3、写出不等式组的解集。(写解)
【巩固提高】
不等式组 的负整数解是( )
A.-2,0,-1; B.-2;
C.-2,-1; D.不能确定.
C
提高练习
1、关于x的不等式组
有解,那么m的取值范围是( )
A、m>8 B、m≥8 C、m<8D、m≤8
C
2、如果不等式组
的解集是x>a,则a_______b。
≥
课堂小结
通过今天的学习,你学会了什么?
你会正确运用吗?
通过这节课的学习,你有什么感受呢,说出来告诉大家.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
