湘教版七年级数学下册第6章 数据的分析 复习课课件(共42张PPT)
文档属性
| 名称 | 湘教版七年级数学下册第6章 数据的分析 复习课课件(共42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 795.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
第6章 复习课
1.说出算术平均数、权数、加权平均数、中位数、众数和方差的概念.
2.会求一组数据的算术平均数、加权平均数、中位数、众数和方差.
3.概述平均数、中位数、众数、方差的差别,初步感受它们在不同情境中的应用.
4.通过解决身边的实际问题,让学生初步认识数学与人类生活的密切联系,以及对人类历史发展的作用.
◎重点:1.说出算术平均数、加权平均数、中位数、众数和方差的概念.
2.会求一组数据的算术平均数、加权平均数、中位数、众数和方差.
◎难点:1.建立本章知识网络.
2.平均数、中位数、众数、方差的应用.
趣谈大数据
身边的人都在谈论大数据,似乎一夜之间,大数据(Big Data)变成一个IT行业中最时髦的词汇.
大数据不是什么完完全全的新生事物,Google的搜索服务就是
一个典型的大数据运用.根据客户的需求,Google实时从全球海量的数字资产(或数字垃圾)中快速找出最可能的答案呈现给你,就是一个最典型的大数据服务.只不过过去这样规模的数据量处理和有商业价值的应用太少,在IT行业没有形成成型的概念.现在随着全球数字化、网络宽带化,互联网应用于各行各业,累积的数据量越来越大,越来越多企业、行业和国家发现,可以利用类似的技术更好地服务客户、发现新商业机会、扩大新市场以及提升效率,才逐步形成大数据这个概念.
在本章,我们主要学习了运用算术平均数、加权平均数、中位数、众数和方差来分析数据.请问:算术平均数、权数、加权平均数、中位数、众数和方差的定义是什么 它们各有什么特点 它们又有哪些区别 它们如何引领我们决策 带着以上疑问,我们开始今天的复习之旅吧!
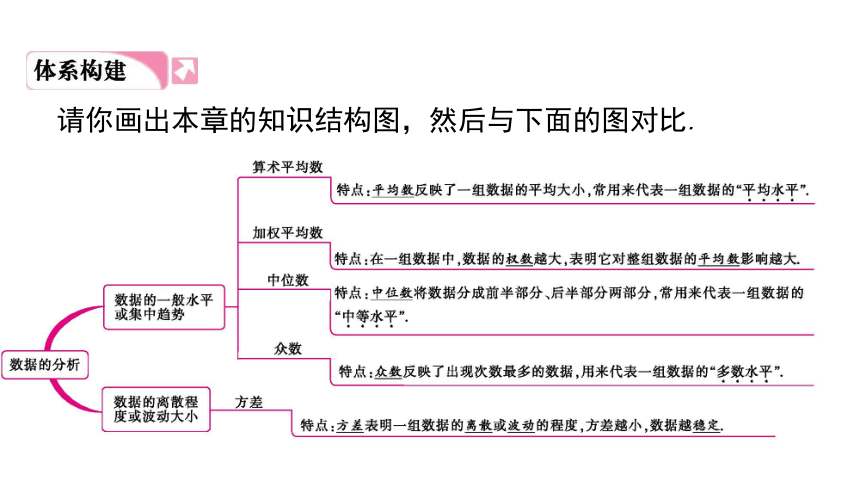
请你画出本章的知识结构图,然后与下面的图对比.
1.一般地,对于n个数x1、x2、x3、…、xn,我们把 叫做这n个数的 ,简称 .通常情况下,用符号 表示.
2.若n个数x1、x2、x3、…、xn的权数分别是a1、a2、a3、…、an,我们把 叫做这n个数的 .其中a1+a2+…+an= .
算术平均数
平均数
x1a1+x2a2+…+xnan
加权平均数
1
3.把一组数据按 的顺序排列,如果数据的个数是 数,那么位于 的数称为这组数据的 ;如果数据的个数是 数,那么位于 的两个数的
称为这组数据的 .
4.在一组数据中,把出现 的数叫做这组数据的 .
从小到大
奇
中间
中位数
偶
中间
平均数
中位数
次数最多
众数
5.一组数据为x1、x2、x3、…、xn,各数与平均数之差的平方的平均值,叫做这组数据的 ,记做s2,即s2= .一般地,一组数据的方差越小,说明这组数据的 或 的程度就越小,这组数据也就越 .
方差
[(x1-)2+(x2-)2+…+(xn-)2]
离散
波动
稳定
平均数与加权平均数
D
1.一组数据:-4,5,1,3,4,3,2的算术平均数是 ( )
A.-2 B.-1 C.1 D.2
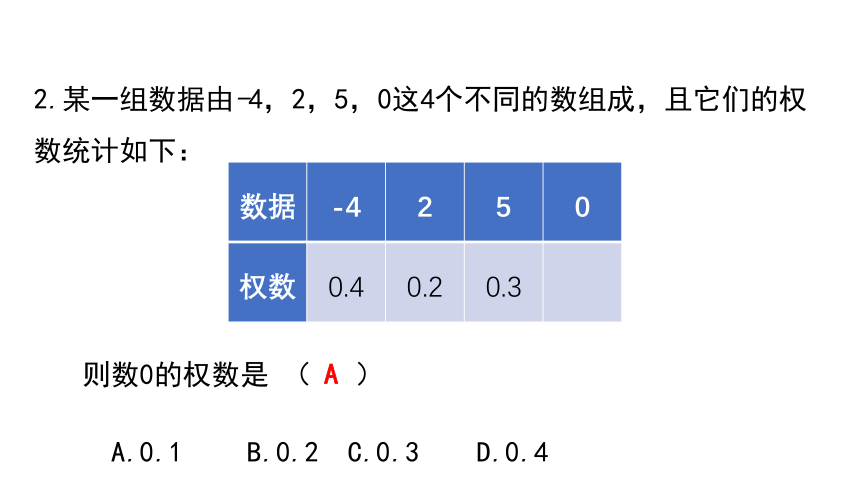
2.某一组数据由-4,2,5,0这4个不同的数组成,且它们的权数统计如下:
数据 -4 2 5 0
权数 0.4 0.2 0.3
则数0的权数是 ( )
A.0.1 B.0.2 C.0.3 D.0.4
A
中位数
B
3.一组数据:3,3,2,2,2,5,5,5,5的中位数是 ( )
A.2 B.3 C.4 D.5
4.某公司10名职工5月份的工资统计如下:
工资(元) 3000 3400 3600 4000
人数(人) 2 3 1 4
则该公司10名职工5月份工资的中位数是 ( )
A.3200元 B.3400元
C.3500元 D.3600元
C
5.一组数据1,2,m,6,5,3的平均数是4,求这组数据的中位数.
解:由题意可知,(1+2+m+6+5+3)÷6=4,解得m=7,所以这一组数据为:1,2,7,6,5,3.将这一组数据按从小到大的顺序排列:1,2,3,5,6,7.这组数据一共有6个数据,所以这组数据的中位数为(3+5)÷2=4.
6.为了解学生一周在校的平均体育锻炼时间,某中学随机调查了50名学生,结果如下表:
时间(小时) 5 6 7 8
人数 12 14 20 4
求这50名学生一周在校的平均体育锻炼时间的中位数.
解:将统计表中的数据按从小到大的顺序排列,可得最中间的两个数分别是6,6,故这50名学生一周在校的平均体育锻炼时间的中位数为(6+6)÷2=6.
众数
B
7.在一组数据3,3,5,2,5,4,2,3,4中, 众数是 ( )
A.2 B.3 C.4 D.5
8.为响应建设“书香校园”的号召,某校随机调查了50名学生平均每天的阅读时间,得到如下结果:每天阅读0.5小时5人,每天阅读1小时18人,每天阅读1.5小时8人,其余的每天阅读2小时.则本次调查中阅读时间的众数是 .
2
9.已知一组数据:3,0,1,2,m,0,2,4的众数是0,求m的值.
解:因为3,0,1,2,m,0,2,4的众数是0,根据众数的定义,0出现的次数一定最多,又2已经出现了2次,所以0出现的次数必多于2次,而在给定的数据中0已经出现了2次,所以m的值是0.
中位数和众数
10.某班10名学生的校服尺寸与对应人数统计如下:
尺寸(cm) 150 155 160 165 170
学生人数(人) 1 4 2 1 2
求这10名学生校服尺寸的众数和中位数.
解:由表格可知,这10名学生校服尺寸的众数是155 cm;
将这10名学生校服尺寸按从小到大的顺序排列:
150,155,155,155,155,160,160,165,170,170.这组数据一共有10个数据,所以这组数据的中位数为(155+160)÷2=157.5 cm.
11.在某中学举行的“中国梦·校园好声音”歌唱比赛中,由于登分人员失误,记录时漏掉了一位同学的比赛成绩,结果统计如下:
编号 ① ② ③ ④ ⑤ ⑥ ⑦
得分 91 93 95 94 93 95
若这组数据的众数只有一个,求这组数据的中位数.
解:因为这组数据的众数只有一个,所以这组数据的众数只能是93或95,所以这一组数据存在以下两种可能:①若这组数据的众数是93,则这组数据为91、93、95、94、93、93、95,将这组数据从小到大排列是91、93、93、93、94、95、95,所以这组数据的中位数是93;②若这组数据的众数是95,则这组数据为91、93、95、94、95、93、95,将这组数据从小到大排列是91,93,93,94,95,95,95,所以这组数据的中位数是94.
方差
12.某体校要从四名射击选手中选拔一名参加省体育运动会,经选拔获得如下数据:
队员 甲 乙 丙 丁
平均成绩 8.3 8.7 8.6 8.6
方差 1.0 1.1 3 1.4
为了获得最好成绩,如果你是教练,你的选择是 ( )
A.甲 B.乙 C.丙 D.丁
B
13.已知一组数据3,2,5,1,4,求这组数据的方差.
解:这组数据的平均数是=×(3+2+5+1+4)=3,
所以这组数据的方差是
s2=×[(3-3)2+(2-3)2+(5-3)2+(1-3)2+(4-3)2]=2.
一组数据的 ,这组数据的 或
的程度就越小,当然也就越 .
方差越小
离散
波动
稳定
14.甲、乙两台机床生产同种零件,10天出的次品数量分别是:
甲:5、6、5、7、7、5、8、6、7、9.
乙:7、8、6、7、5、7、6、6、7、6.
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好.
解:由题意可知,=×(5×3+6×2+7×3+8+9)=6.5,=×(7×4+8+6×4+5)=6.5,=×[(5-6.5)2×3+(6-6.5)2×2+(7-6.5)2×3+(8-6.5)2+(9-6.5)2]=1.65,=×[(7-6.5)2×4+(8-6.5)2+(6-6.5)2×4+(5-6.5)2]=0.65,
因为﹥,所以乙机床性能较好.
15.某校生物兴趣小组20位学生在实验操作中的得分情况如下表:
平均数、中位数和众数
得分(分) 7 8 10 9
人数(人) 6 4 3 7
求这组数据的平均数、众数、中位数.
解:由题意可知,这组数据的众数是9;将这一组数据按从小到大的顺序排列,排在第10、11位的数分别是8和9,所以这一组数据的中位数是(8+9)÷2=8.5,这一组数据的平均数是
=×(7×6+8×4+10×3+9×7)=8.35.
1.甲、乙、丙三人进行跳远比赛,每人跳远的平均成绩都是2.12米,方差分别是=0.32,=0.23,=3.02,则跳远成绩最稳定的是 .
乙
2.某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了10次测试,测试成绩(单位:环)如下表:
甲:7、8、10、7、7、6、8、9、8、10.
乙:7、10、7、7、9、7、9、8、9、7.
分别计算出两个样本的平均数和方差,根据你的计算判断派谁参加较好.
解:由题意可知=×(7×3+8×3+10×2+6+9)=8,=×(7×5+10+9×3+8)=8,
=×[(7-8)2×3+(8-8)2×3+(10-8)2×2+(6-8)2
+ (9-8)2]=1.6,
=×[(7-8)2×5+(10-8)2+(9-8)2×3+(8-8)2]=1.2,
因为﹥,所以派乙参加较好.
3.一组数据由三个不同的数据3,6,5组成,其中3,5的权数依次为0.2,0.3,则这一组数据的加权平均数是 .
4.一组数据由4个不同的数据1、5、0、2组成,其中1、5、0、2的权数之比依次为2∶3∶4∶1,则这组数据的众数是 .
0
5.1
5.甲、乙、丙三名跳高运动员考核赛的平均成绩(单位:米)及方差如下:
队员 甲 乙 丙
平均成绩 1.55 1.54 1.55
方差 1.2 3 11
若从以上四人中选一人参加比赛,你的选择是 .
甲
6.为了解学生一周在校的平均体育锻炼时间,某中学随机调查了40名学生,结果如下表:
时间(小时) 5 6 7 8
人数 14 7 13
求这40名学生这一周在校的平均体育锻炼时间的中位数.
解:由题意可知,一周在校的平均体育锻炼时间为6小时的学生人数为40-14-7-13=6,将统计表中的数按从小到大的顺序排列后,可得最中间两个分别是6,7,故这40名学生一周在校的平均体育锻炼时间的中位数为(6+7)÷2=6.5.
7.2021年下学期某班一共进行了四次考试,李文和刘平的成绩统计如下:
学生 单元 测试1 期中 考试 单元 测试2 期末
考试
李文 85 90 80 85
刘平 70 90 90 90
(1)在这4次考试中,谁的成绩比较稳定
解:(1)由题意可知,=×(85+90+80+85)=85,
=×(70+90+90+90)=85,
所以=×[(85-85)2×2+(90-85)2+(80-85)2]=12.5,=×[(70-85)2+(90-85)2×3]=75,
所以李文的成绩比较稳定.
(2)若学生的期末总评成绩按单元测试1占10%,期中考试占30%,单元测试2占20%,期末考试占40%计算,谁的期末总评成绩更高
(2)李文的期末总评成绩为85×10%+90×30%+80×20%+85×40%=85.5,刘平的期末总评成绩为70×10%+90×30%+90×20%+90×40%=88,所以刘平的期末总评成绩更高.
8.一组数据的平均数为2,若将这组数据中的每一个数都乘以2后再减去3可得一组新的数据,则新数据的平均数是 ( )
A.4 B.3 C.2 D.1
D
9.在最近的一次生物测试中,小莉考了93分,从而使本学期之前所有的生物测试平均分由73分提高到78分,若她想在下次考试中把本学期的平均分提高到81分以上,则下次考试时她至少要考 分.
93
第6章 复习课
1.说出算术平均数、权数、加权平均数、中位数、众数和方差的概念.
2.会求一组数据的算术平均数、加权平均数、中位数、众数和方差.
3.概述平均数、中位数、众数、方差的差别,初步感受它们在不同情境中的应用.
4.通过解决身边的实际问题,让学生初步认识数学与人类生活的密切联系,以及对人类历史发展的作用.
◎重点:1.说出算术平均数、加权平均数、中位数、众数和方差的概念.
2.会求一组数据的算术平均数、加权平均数、中位数、众数和方差.
◎难点:1.建立本章知识网络.
2.平均数、中位数、众数、方差的应用.
趣谈大数据
身边的人都在谈论大数据,似乎一夜之间,大数据(Big Data)变成一个IT行业中最时髦的词汇.
大数据不是什么完完全全的新生事物,Google的搜索服务就是
一个典型的大数据运用.根据客户的需求,Google实时从全球海量的数字资产(或数字垃圾)中快速找出最可能的答案呈现给你,就是一个最典型的大数据服务.只不过过去这样规模的数据量处理和有商业价值的应用太少,在IT行业没有形成成型的概念.现在随着全球数字化、网络宽带化,互联网应用于各行各业,累积的数据量越来越大,越来越多企业、行业和国家发现,可以利用类似的技术更好地服务客户、发现新商业机会、扩大新市场以及提升效率,才逐步形成大数据这个概念.
在本章,我们主要学习了运用算术平均数、加权平均数、中位数、众数和方差来分析数据.请问:算术平均数、权数、加权平均数、中位数、众数和方差的定义是什么 它们各有什么特点 它们又有哪些区别 它们如何引领我们决策 带着以上疑问,我们开始今天的复习之旅吧!
请你画出本章的知识结构图,然后与下面的图对比.
1.一般地,对于n个数x1、x2、x3、…、xn,我们把 叫做这n个数的 ,简称 .通常情况下,用符号 表示.
2.若n个数x1、x2、x3、…、xn的权数分别是a1、a2、a3、…、an,我们把 叫做这n个数的 .其中a1+a2+…+an= .
算术平均数
平均数
x1a1+x2a2+…+xnan
加权平均数
1
3.把一组数据按 的顺序排列,如果数据的个数是 数,那么位于 的数称为这组数据的 ;如果数据的个数是 数,那么位于 的两个数的
称为这组数据的 .
4.在一组数据中,把出现 的数叫做这组数据的 .
从小到大
奇
中间
中位数
偶
中间
平均数
中位数
次数最多
众数
5.一组数据为x1、x2、x3、…、xn,各数与平均数之差的平方的平均值,叫做这组数据的 ,记做s2,即s2= .一般地,一组数据的方差越小,说明这组数据的 或 的程度就越小,这组数据也就越 .
方差
[(x1-)2+(x2-)2+…+(xn-)2]
离散
波动
稳定
平均数与加权平均数
D
1.一组数据:-4,5,1,3,4,3,2的算术平均数是 ( )
A.-2 B.-1 C.1 D.2
2.某一组数据由-4,2,5,0这4个不同的数组成,且它们的权数统计如下:
数据 -4 2 5 0
权数 0.4 0.2 0.3
则数0的权数是 ( )
A.0.1 B.0.2 C.0.3 D.0.4
A
中位数
B
3.一组数据:3,3,2,2,2,5,5,5,5的中位数是 ( )
A.2 B.3 C.4 D.5
4.某公司10名职工5月份的工资统计如下:
工资(元) 3000 3400 3600 4000
人数(人) 2 3 1 4
则该公司10名职工5月份工资的中位数是 ( )
A.3200元 B.3400元
C.3500元 D.3600元
C
5.一组数据1,2,m,6,5,3的平均数是4,求这组数据的中位数.
解:由题意可知,(1+2+m+6+5+3)÷6=4,解得m=7,所以这一组数据为:1,2,7,6,5,3.将这一组数据按从小到大的顺序排列:1,2,3,5,6,7.这组数据一共有6个数据,所以这组数据的中位数为(3+5)÷2=4.
6.为了解学生一周在校的平均体育锻炼时间,某中学随机调查了50名学生,结果如下表:
时间(小时) 5 6 7 8
人数 12 14 20 4
求这50名学生一周在校的平均体育锻炼时间的中位数.
解:将统计表中的数据按从小到大的顺序排列,可得最中间的两个数分别是6,6,故这50名学生一周在校的平均体育锻炼时间的中位数为(6+6)÷2=6.
众数
B
7.在一组数据3,3,5,2,5,4,2,3,4中, 众数是 ( )
A.2 B.3 C.4 D.5
8.为响应建设“书香校园”的号召,某校随机调查了50名学生平均每天的阅读时间,得到如下结果:每天阅读0.5小时5人,每天阅读1小时18人,每天阅读1.5小时8人,其余的每天阅读2小时.则本次调查中阅读时间的众数是 .
2
9.已知一组数据:3,0,1,2,m,0,2,4的众数是0,求m的值.
解:因为3,0,1,2,m,0,2,4的众数是0,根据众数的定义,0出现的次数一定最多,又2已经出现了2次,所以0出现的次数必多于2次,而在给定的数据中0已经出现了2次,所以m的值是0.
中位数和众数
10.某班10名学生的校服尺寸与对应人数统计如下:
尺寸(cm) 150 155 160 165 170
学生人数(人) 1 4 2 1 2
求这10名学生校服尺寸的众数和中位数.
解:由表格可知,这10名学生校服尺寸的众数是155 cm;
将这10名学生校服尺寸按从小到大的顺序排列:
150,155,155,155,155,160,160,165,170,170.这组数据一共有10个数据,所以这组数据的中位数为(155+160)÷2=157.5 cm.
11.在某中学举行的“中国梦·校园好声音”歌唱比赛中,由于登分人员失误,记录时漏掉了一位同学的比赛成绩,结果统计如下:
编号 ① ② ③ ④ ⑤ ⑥ ⑦
得分 91 93 95 94 93 95
若这组数据的众数只有一个,求这组数据的中位数.
解:因为这组数据的众数只有一个,所以这组数据的众数只能是93或95,所以这一组数据存在以下两种可能:①若这组数据的众数是93,则这组数据为91、93、95、94、93、93、95,将这组数据从小到大排列是91、93、93、93、94、95、95,所以这组数据的中位数是93;②若这组数据的众数是95,则这组数据为91、93、95、94、95、93、95,将这组数据从小到大排列是91,93,93,94,95,95,95,所以这组数据的中位数是94.
方差
12.某体校要从四名射击选手中选拔一名参加省体育运动会,经选拔获得如下数据:
队员 甲 乙 丙 丁
平均成绩 8.3 8.7 8.6 8.6
方差 1.0 1.1 3 1.4
为了获得最好成绩,如果你是教练,你的选择是 ( )
A.甲 B.乙 C.丙 D.丁
B
13.已知一组数据3,2,5,1,4,求这组数据的方差.
解:这组数据的平均数是=×(3+2+5+1+4)=3,
所以这组数据的方差是
s2=×[(3-3)2+(2-3)2+(5-3)2+(1-3)2+(4-3)2]=2.
一组数据的 ,这组数据的 或
的程度就越小,当然也就越 .
方差越小
离散
波动
稳定
14.甲、乙两台机床生产同种零件,10天出的次品数量分别是:
甲:5、6、5、7、7、5、8、6、7、9.
乙:7、8、6、7、5、7、6、6、7、6.
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好.
解:由题意可知,=×(5×3+6×2+7×3+8+9)=6.5,=×(7×4+8+6×4+5)=6.5,=×[(5-6.5)2×3+(6-6.5)2×2+(7-6.5)2×3+(8-6.5)2+(9-6.5)2]=1.65,=×[(7-6.5)2×4+(8-6.5)2+(6-6.5)2×4+(5-6.5)2]=0.65,
因为﹥,所以乙机床性能较好.
15.某校生物兴趣小组20位学生在实验操作中的得分情况如下表:
平均数、中位数和众数
得分(分) 7 8 10 9
人数(人) 6 4 3 7
求这组数据的平均数、众数、中位数.
解:由题意可知,这组数据的众数是9;将这一组数据按从小到大的顺序排列,排在第10、11位的数分别是8和9,所以这一组数据的中位数是(8+9)÷2=8.5,这一组数据的平均数是
=×(7×6+8×4+10×3+9×7)=8.35.
1.甲、乙、丙三人进行跳远比赛,每人跳远的平均成绩都是2.12米,方差分别是=0.32,=0.23,=3.02,则跳远成绩最稳定的是 .
乙
2.某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了10次测试,测试成绩(单位:环)如下表:
甲:7、8、10、7、7、6、8、9、8、10.
乙:7、10、7、7、9、7、9、8、9、7.
分别计算出两个样本的平均数和方差,根据你的计算判断派谁参加较好.
解:由题意可知=×(7×3+8×3+10×2+6+9)=8,=×(7×5+10+9×3+8)=8,
=×[(7-8)2×3+(8-8)2×3+(10-8)2×2+(6-8)2
+ (9-8)2]=1.6,
=×[(7-8)2×5+(10-8)2+(9-8)2×3+(8-8)2]=1.2,
因为﹥,所以派乙参加较好.
3.一组数据由三个不同的数据3,6,5组成,其中3,5的权数依次为0.2,0.3,则这一组数据的加权平均数是 .
4.一组数据由4个不同的数据1、5、0、2组成,其中1、5、0、2的权数之比依次为2∶3∶4∶1,则这组数据的众数是 .
0
5.1
5.甲、乙、丙三名跳高运动员考核赛的平均成绩(单位:米)及方差如下:
队员 甲 乙 丙
平均成绩 1.55 1.54 1.55
方差 1.2 3 11
若从以上四人中选一人参加比赛,你的选择是 .
甲
6.为了解学生一周在校的平均体育锻炼时间,某中学随机调查了40名学生,结果如下表:
时间(小时) 5 6 7 8
人数 14 7 13
求这40名学生这一周在校的平均体育锻炼时间的中位数.
解:由题意可知,一周在校的平均体育锻炼时间为6小时的学生人数为40-14-7-13=6,将统计表中的数按从小到大的顺序排列后,可得最中间两个分别是6,7,故这40名学生一周在校的平均体育锻炼时间的中位数为(6+7)÷2=6.5.
7.2021年下学期某班一共进行了四次考试,李文和刘平的成绩统计如下:
学生 单元 测试1 期中 考试 单元 测试2 期末
考试
李文 85 90 80 85
刘平 70 90 90 90
(1)在这4次考试中,谁的成绩比较稳定
解:(1)由题意可知,=×(85+90+80+85)=85,
=×(70+90+90+90)=85,
所以=×[(85-85)2×2+(90-85)2+(80-85)2]=12.5,=×[(70-85)2+(90-85)2×3]=75,
所以李文的成绩比较稳定.
(2)若学生的期末总评成绩按单元测试1占10%,期中考试占30%,单元测试2占20%,期末考试占40%计算,谁的期末总评成绩更高
(2)李文的期末总评成绩为85×10%+90×30%+80×20%+85×40%=85.5,刘平的期末总评成绩为70×10%+90×30%+90×20%+90×40%=88,所以刘平的期末总评成绩更高.
8.一组数据的平均数为2,若将这组数据中的每一个数都乘以2后再减去3可得一组新的数据,则新数据的平均数是 ( )
A.4 B.3 C.2 D.1
D
9.在最近的一次生物测试中,小莉考了93分,从而使本学期之前所有的生物测试平均分由73分提高到78分,若她想在下次考试中把本学期的平均分提高到81分以上,则下次考试时她至少要考 分.
93
