苏科版七年级数学下册 12.2 证明 教案
文档属性
| 名称 | 苏科版七年级数学下册 12.2 证明 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 70.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览

文档简介
12.2 证明
一、设计思路
“说理”在数学教学中居于重要的地位.从生活问题到数学问题,让学生认识到仅凭观察、实验、归纳、类比得到的结论,其正确性有待确认,从而引导学生认识到“说理”是确定一个数学结论正确性的有力工具,进而学会如何说理,做到步步有据.通过情境1、2让学生“认识到说理的必要性”是设计的重点,对情境2的几个问题的探索活动,让学生学会“说理要步步有据”是本节课的难点.
二、目标设计
1. 经历探索一些问题时,由于“直观判断不可靠”、“直观无法做出确定判断”,但运用已有的数学知识和方法可以确定一个数学结论的正确性的过程,初步感受说理的必要性.
2. 尝试用说理的方法解决问题,体验说理必须步步有据,培养学生严密分析问题的能力.
3. 通过实验、操作、探索,培养学生辨证分析问题的能力和逆向思维的能力;懂得任何事物都是正反两方面的对立统一体.
三、教具准备
水杯、筷子、数学实验手册、课件
四、教学过程
一、情境创设:
前天,二班洪美善向我告状说,水杯被同学弄坏了。我就问,你知道是谁弄坏的呢?她说,听有人说第四节课只有马炳文在教室,应该就是他弄坏的。
你们认为水杯到底是不是马炳文弄坏的?
向水杯中倒水,观察水杯中筷子的变化,说说看。
二、探究活动:
1、探究活动一:
先猜一猜图中的两条线段AB与CD哪一条长一些?请再量一量证实你的猜想.
2、探究活动二:
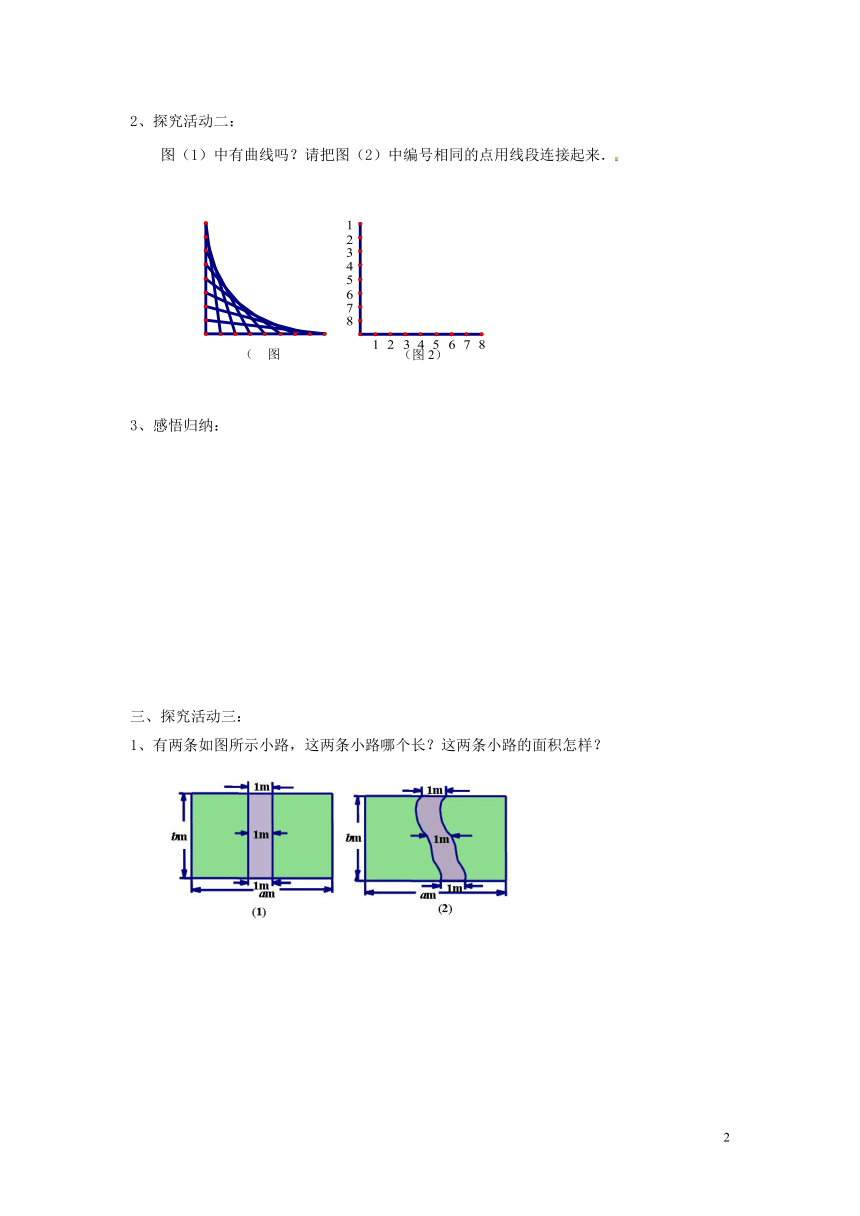
图(1)中有曲线吗?请把图(2)中编号相同的点用线段连接起来.
(
(图
1
)
(图
2
)
)
3、感悟归纳:
三、探究活动三:
1、有两条如图所示小路,这两条小路哪个长?这两条小路的面积怎样?
2、问题1 当x=-2、0、1、0.5时,计算代数式的值。
问题2 换几个数再试试,你发现了什么?你能说明理由吗?
问题3 你认为以下结论正确吗?你能说明理由吗?
(1)无论x取什么数,代数式的值总是偶数;
(2)无论x取什么数,代数式的值总是正数
(3)无论x取什么数,代数式的值大于1.
3、数学实验
(1)在提供的模板中取两个直角三角形和两个直角梯形,按图①拼成8×8的正方形,用胶带粘好.
(
(图①)
(图②)
)(2)用同样的两个直角三角形和两个直角梯形,能按图②恰好拼成13×5的矩形吗?动手试一试!
三、随堂练习:
1、数学实验
如图:(1)画∠AOB=90°,并画∠AOB的角平分线OC.
(2)将三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别交于点E、F,并比较PE、PF的长度.
(3)把三角尺绕点P旋转,比较PE与PF的长度.
你能得到什么结论?你的结论一定成立吗?与同学交流.
2、甲乙两同学在月牙岛平行四边形ABCD区域内捡垃圾。老师分给甲同学①、③两区域,乙同学② 、④两区域,老师这样分工公平吗?
4
一、设计思路
“说理”在数学教学中居于重要的地位.从生活问题到数学问题,让学生认识到仅凭观察、实验、归纳、类比得到的结论,其正确性有待确认,从而引导学生认识到“说理”是确定一个数学结论正确性的有力工具,进而学会如何说理,做到步步有据.通过情境1、2让学生“认识到说理的必要性”是设计的重点,对情境2的几个问题的探索活动,让学生学会“说理要步步有据”是本节课的难点.
二、目标设计
1. 经历探索一些问题时,由于“直观判断不可靠”、“直观无法做出确定判断”,但运用已有的数学知识和方法可以确定一个数学结论的正确性的过程,初步感受说理的必要性.
2. 尝试用说理的方法解决问题,体验说理必须步步有据,培养学生严密分析问题的能力.
3. 通过实验、操作、探索,培养学生辨证分析问题的能力和逆向思维的能力;懂得任何事物都是正反两方面的对立统一体.
三、教具准备
水杯、筷子、数学实验手册、课件
四、教学过程
一、情境创设:
前天,二班洪美善向我告状说,水杯被同学弄坏了。我就问,你知道是谁弄坏的呢?她说,听有人说第四节课只有马炳文在教室,应该就是他弄坏的。
你们认为水杯到底是不是马炳文弄坏的?
向水杯中倒水,观察水杯中筷子的变化,说说看。
二、探究活动:
1、探究活动一:
先猜一猜图中的两条线段AB与CD哪一条长一些?请再量一量证实你的猜想.
2、探究活动二:
图(1)中有曲线吗?请把图(2)中编号相同的点用线段连接起来.
(
(图
1
)
(图
2
)
)
3、感悟归纳:
三、探究活动三:
1、有两条如图所示小路,这两条小路哪个长?这两条小路的面积怎样?
2、问题1 当x=-2、0、1、0.5时,计算代数式的值。
问题2 换几个数再试试,你发现了什么?你能说明理由吗?
问题3 你认为以下结论正确吗?你能说明理由吗?
(1)无论x取什么数,代数式的值总是偶数;
(2)无论x取什么数,代数式的值总是正数
(3)无论x取什么数,代数式的值大于1.
3、数学实验
(1)在提供的模板中取两个直角三角形和两个直角梯形,按图①拼成8×8的正方形,用胶带粘好.
(
(图①)
(图②)
)(2)用同样的两个直角三角形和两个直角梯形,能按图②恰好拼成13×5的矩形吗?动手试一试!
三、随堂练习:
1、数学实验
如图:(1)画∠AOB=90°,并画∠AOB的角平分线OC.
(2)将三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别交于点E、F,并比较PE、PF的长度.
(3)把三角尺绕点P旋转,比较PE与PF的长度.
你能得到什么结论?你的结论一定成立吗?与同学交流.
2、甲乙两同学在月牙岛平行四边形ABCD区域内捡垃圾。老师分给甲同学①、③两区域,乙同学② 、④两区域,老师这样分工公平吗?
4
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
