2021-2022学年人教版数学九年级下册《第29章投影与视图》单元测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册《第29章投影与视图》单元测试(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 274.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 12:10:18 | ||
图片预览

文档简介
2021-2022学年人教新版九年级下册数学《第29章 投影与视图》单元测试卷
一.选择题(共11小题,满分33分)
1.如图所示,在房子外的屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区在( )
A.△ACE B.△BFD C.四边形BCED D.△ABD
2.如图所示的几何体的从上面看到的形状图是( )
A. B. C. D.
3.如图,下列几何体的左视图不是矩形的是( )
A. B. C. D.
4.如图所示几何体的主视图是( )
A. B. C. D.
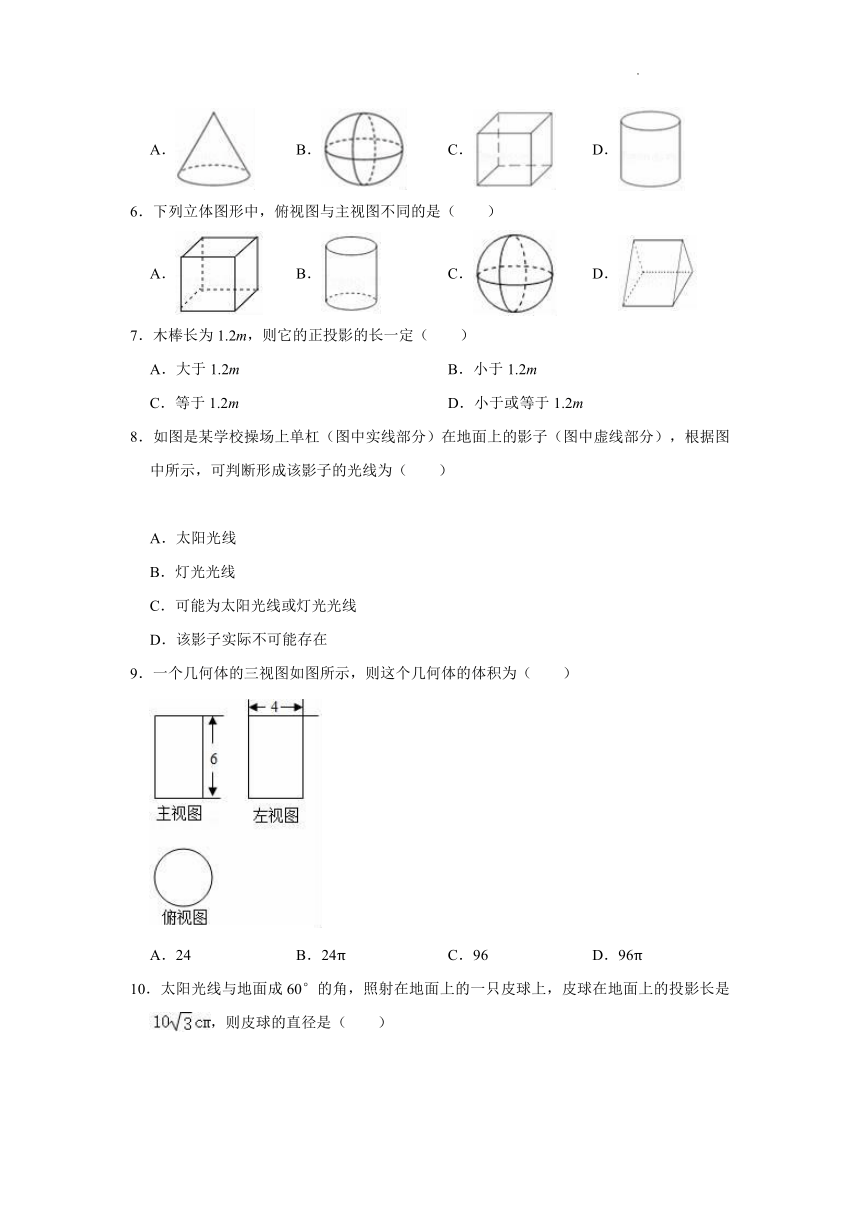
5.下列四个几何体中,左视图为圆的是( )
A. B. C. D.
6.下列立体图形中,俯视图与主视图不同的是( )
A. B. C. D.
7.木棒长为1.2m,则它的正投影的长一定( )
A.大于1.2m B.小于1.2m
C.等于1.2m D.小于或等于1.2m
8.如图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线
B.灯光光线
C.可能为太阳光线或灯光光线
D.该影子实际不可能存在
9.一个几何体的三视图如图所示,则这个几何体的体积为( )
A.24 B.24π C.96 D.96π
10.太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,则皮球的直径是( )
A. B.15 C.10 D.
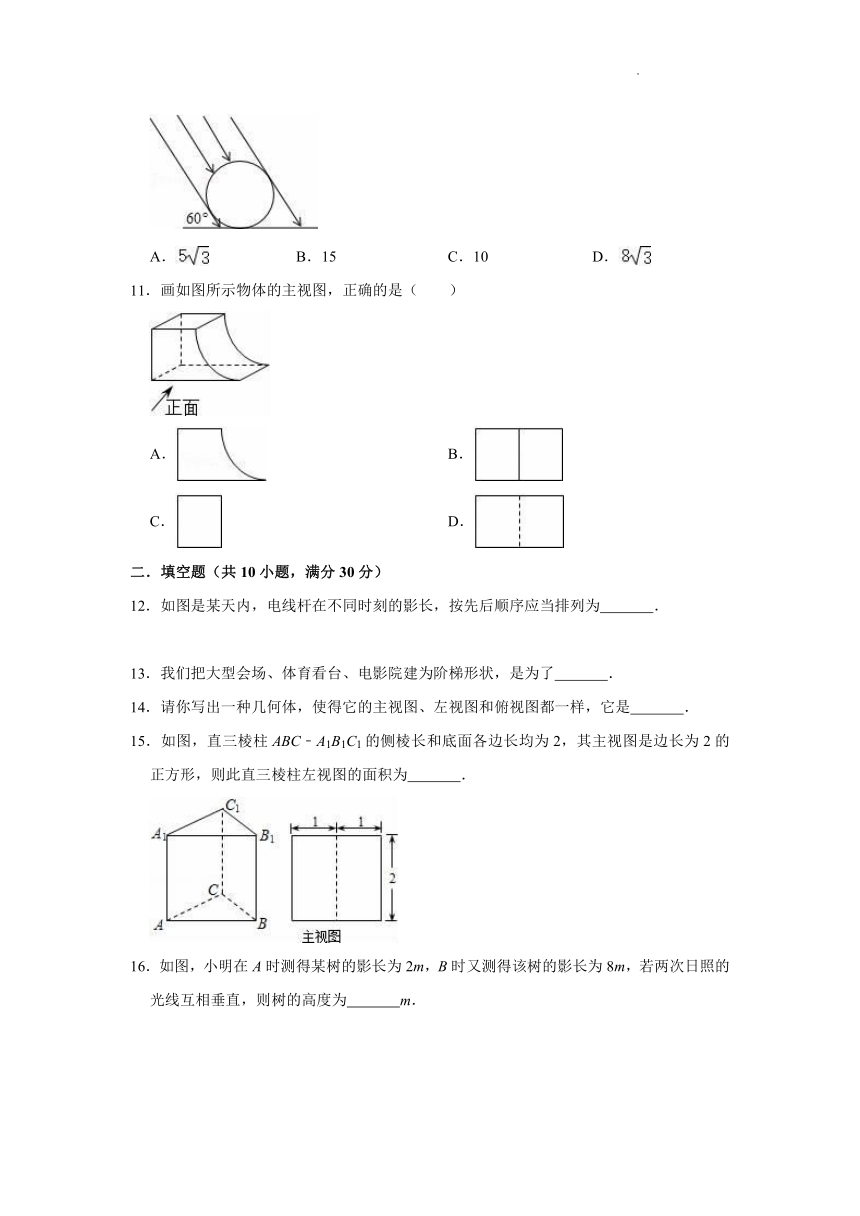
11.画如图所示物体的主视图,正确的是( )
A. B.
C. D.
二.填空题(共10小题,满分30分)
12.如图是某天内,电线杆在不同时刻的影长,按先后顺序应当排列为 .
13.我们把大型会场、体育看台、电影院建为阶梯形状,是为了 .
14.请你写出一种几何体,使得它的主视图、左视图和俯视图都一样,它是 .
15.如图,直三棱柱ABC﹣A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为 .
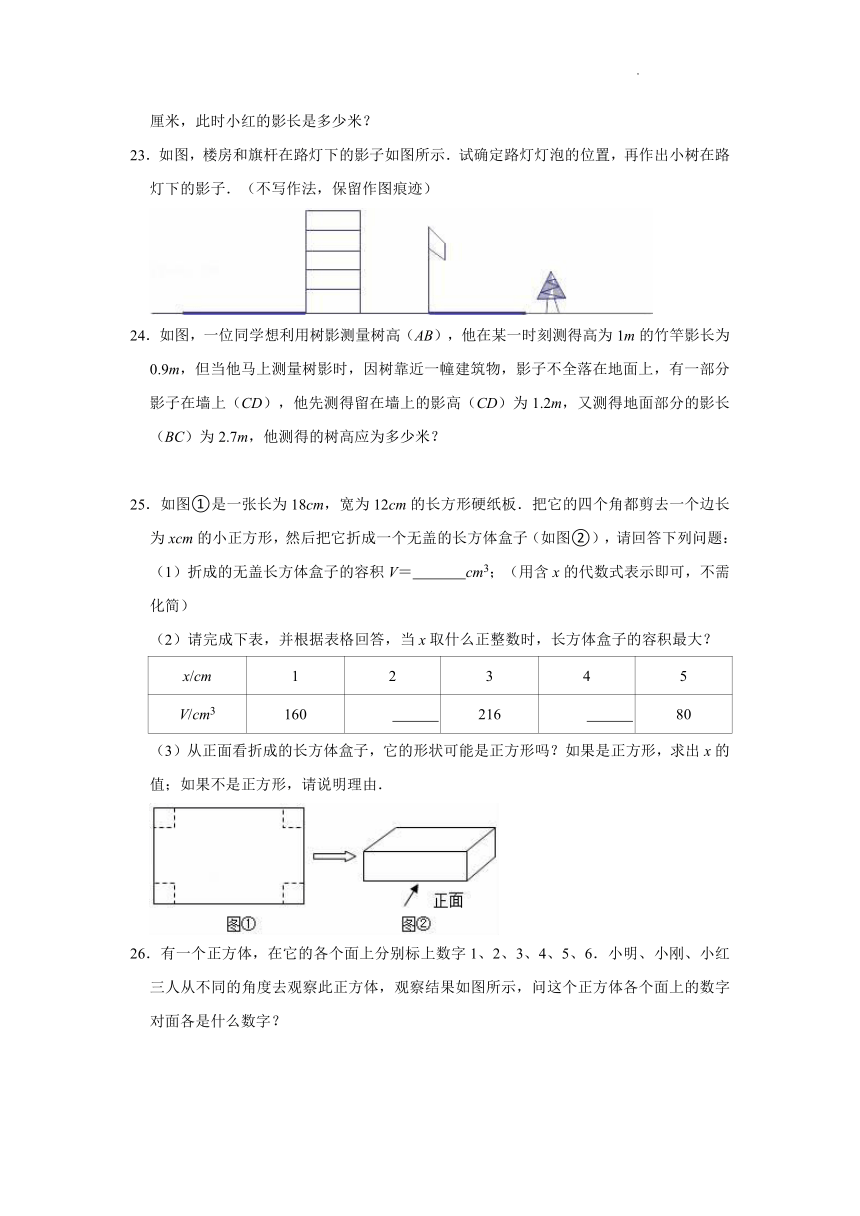
16.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为 m.
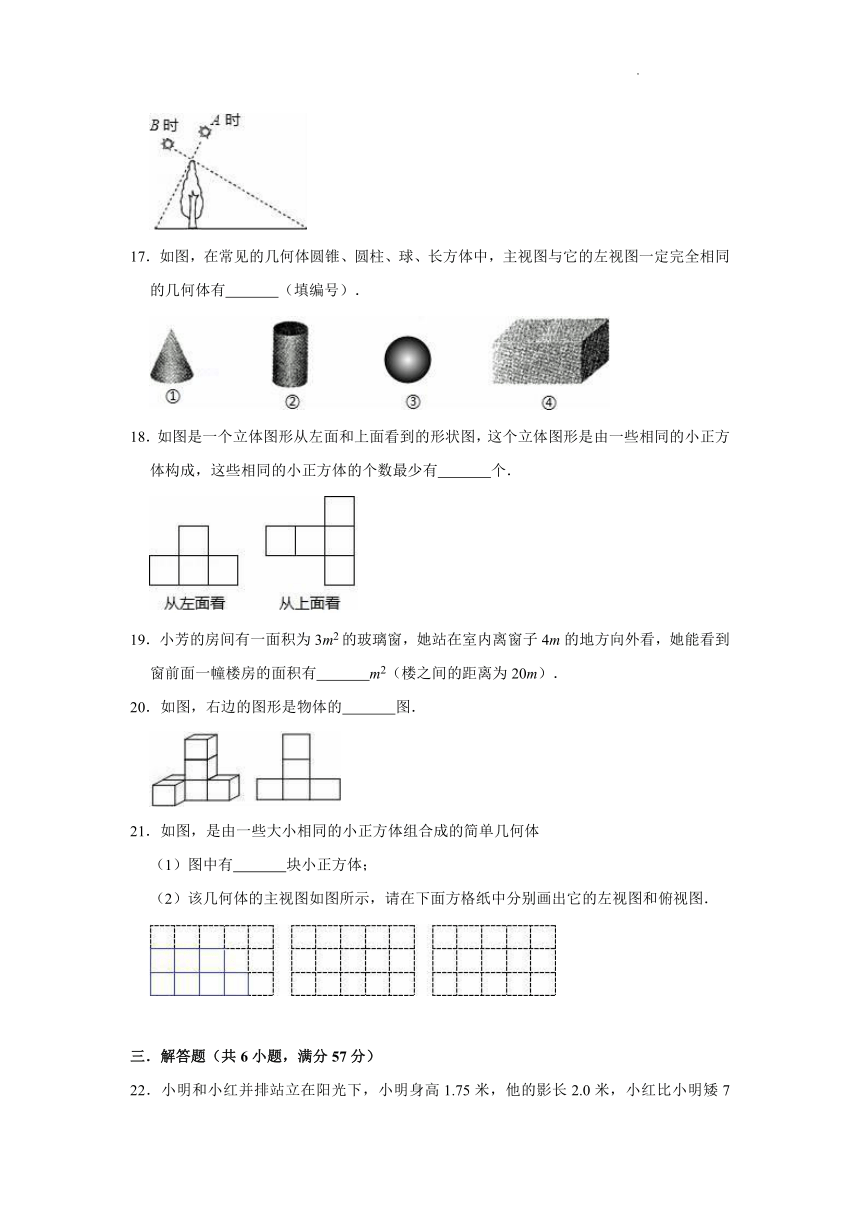
17.如图,在常见的几何体圆锥、圆柱、球、长方体中,主视图与它的左视图一定完全相同的几何体有 (填编号).
18.如图是一个立体图形从左面和上面看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最少有 个.
19.小芳的房间有一面积为3m2的玻璃窗,她站在室内离窗子4m的地方向外看,她能看到窗前面一幢楼房的面积有 m2(楼之间的距离为20m).
20.如图,右边的图形是物体的 图.
21.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
三.解答题(共6小题,满分57分)
22.小明和小红并排站立在阳光下,小明身高1.75米,他的影长2.0米,小红比小明矮7厘米,此时小红的影长是多少米?
23.如图,楼房和旗杆在路灯下的影子如图所示.试确定路灯灯泡的位置,再作出小树在路灯下的影子.(不写作法,保留作图痕迹)
24.如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
25.如图①是一张长为18cm,宽为12cm的长方形硬纸板.把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积V= cm3;(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大?
x/cm 1 2 3 4 5
V/cm3 160 216 80
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出x的值;如果不是正方形,请说明理由.
26.有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6.小明、小刚、小红三人从不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的数字对面各是什么数字?
27.如图是某比赛场馆的平面图,根据距离比赛场地的远近和视角的不同,将观赛场地划分成A、B、C三个不同的票价区.其中与场地边缘MN的视角大于或等于45°,并且距场地边缘MN的距离不超过30m的区域划分为A票区,B票区如图所示,剩下的为C票区.(π取3)
(1)请你利用尺规作图,在观赛场地中,作出A票区所在的区域(只要作出图形,保留作图痕迹,不要求写作法);
(2)如果每个座位所占的平均面积是0.8平方米,请估算A票区有多少个座位.
参考答案与试题解析
一.选择题(共11小题,满分33分)
1.解:由图片可知,E视点的盲区应该在三角形ABD的区域内.
故选:D.
2.解:如图所示的几何体的从上面看到的形状图是.
故选:D.
3.解:A、圆柱的左视图是矩形,故本选项不符合题意;
B、三棱锥的左视图是三角形,故本选项符合题意;
C、三棱柱的左视图是矩形,故本选项不符合题意;
D、正方体的左视图是正方形,故本选项不符合题意.
故选:B.
4.解:几何体的主视图为.
故选:B.
5.解:因为圆柱的左视图是矩形,圆锥的左视图是等腰三角形,球的左视图是圆,正方体的左视图是正方形,
所以,左视图是圆的几何体是球.
故选:B.
6.解:A.俯视图与主视图都是正方形,故选项A不合题意;
B.俯视图是圆,主视图是长方形,故选项B合题意;
C.俯视图与主视图都是圆,故选项C不合题意;
D.俯视图和主视图是长方形;故选项D不符合题意;
故选:B.
7.解:正投影的长度与木棒的摆放角度有关系,但无论怎样摆都不会超过1.2 m.
故选:D.
8.解:若形成的影子是由太阳光照射形成的影子,则两直线一定平行;若形成的影子是由灯光照射而形成的影子,则两直线一定相交.所以可判断形成该影子的光线为灯光光线.故选:B.
9.解:由三视图确定该几何体是圆柱体,底面半径是4÷2=2,高是6,
则这个几何体的体积为π×22×6=24π.
故选:B.
10.解:由题意得:DC=2R,DE=10,∠CED=60°,
∴可得:DC=DEsin60°=15.
故选:B.
11.解:从正面看得到的图形是A.
故选:A.
二.填空题(共10小题,满分30分)
12.解:根据北半球上太阳光下的影子变化的规律,
从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.
可得顺序为DABC.
13.解:把大型会场、体育看台、电影院建为阶梯形状,是为了使后面的观众有更大的视野,从而减小盲区.
14.解:球的3个视图都为圆;
正方体的3个视图都为正方形;
所以主视图、左视图和俯视图都一样的几何体为球、正方体等.
15.解:此直三棱柱左视图是长为2,宽为AB边上的高的矩形,
∵底面各边长均为2,
∴△ABC是等边三角形,AB边上的高为2×=,
∴此直三棱柱左视图的面积=2×=2.
故答案为:2.
16.解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED FD,
代入数据可得DC2=16,
DC=4;
故答案为:4.
17.解:①圆锥主视图是三角形,左视图也是三角形,
②圆柱的主视图和左视图都是矩形;
③球的主视图和左视图都是圆形;
④长方体的主视图是矩形,左视图也是矩形,但是长和宽不一定相同,
故选:①②③.
18.解:根据俯视图可得:底层正方体最少5个正方体,
根据左视图可得:第二层最少有1个正方体;
则构成这个立体图形的小正方体的个数最少为5+1=6(个).
故答案为:6.
19.解:根据题意:她能看到窗前面一幢楼房的图形与玻璃窗的外形应该相似,且相似比为=6,
故面积的比为36;
故她能看到窗前面一幢楼房的面积有36×3=108(m2).
20.解:由三视图的概念,可得该图形的左视图是竖着的三个正方形;
俯视图是两排,下右侧由一个正方形,上面并排三个正方形;
所以右边的图形是物体的主视图.
21.解:(1)根据如图所示即可数出有11块小正方体;
(2)如图所示;左视图,俯视图分别如下图:
故答案为:(1)11.
三.解答题(共6小题,满分57分)
22.解:设小红的影长是x米,
根据题意得=,
解得x=1.92.
答:小红的影长是1.92米.
23.解:
24.解:作AD和BC的延长线交于点E,
设墙上的影高CD落在地面上时的长度为xm,树高为hm,
∵某一时刻测得长为1m的竹竿影长为0.9m,墙上的影高CD为1.2m,
∴,解得x=1.08(m),
∴树的影长为:1.08+2.7=3.78(m),
∴,解得h=4.2(m).
答:测得的树高为4.2米.
25.解:(1)由题意得,长方体盒子的长(18﹣2x)、宽(12﹣2x)、高x,因此体积为:(18﹣2x) (12﹣2x) x,
故答案为:(18﹣2x) (12﹣2x) x,
(2)把x=2代入(18﹣2x) (12﹣2x) x得,(18﹣2x) (12﹣2x) x=14×8×2=224,
把x=4代入(18﹣2x) (12﹣2x) x得,(18﹣2x) (12﹣2x) x=10×4×4=160,
故答案为:224,160;
(3)它的形状不可能是正方形,
当18﹣2x=x时,即x=6,而当x=6时,图①的长边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
26.解:从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5面,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
27.解:(1)如图,以线段MN、EF与、所围成的区域就是所作的A票区.
(2)连接OM、ON、OE、OF,设MN的中垂线与MN、EF分别相交于点G和H.
由题意,得∠MON=90°.
∵OG⊥MN,OH⊥EF,
OG=OH=15,
∴∠EOF=∠MON=90°.
∴.
∴SA=(S扇形FOM+S扇形EON)+(S△OMN+S△EOF)=πr2+r2≈1125(米2).
∴1125÷0.8≈1406.
∴A票区约有1406个座位.
一.选择题(共11小题,满分33分)
1.如图所示,在房子外的屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区在( )
A.△ACE B.△BFD C.四边形BCED D.△ABD
2.如图所示的几何体的从上面看到的形状图是( )
A. B. C. D.
3.如图,下列几何体的左视图不是矩形的是( )
A. B. C. D.
4.如图所示几何体的主视图是( )
A. B. C. D.
5.下列四个几何体中,左视图为圆的是( )
A. B. C. D.
6.下列立体图形中,俯视图与主视图不同的是( )
A. B. C. D.
7.木棒长为1.2m,则它的正投影的长一定( )
A.大于1.2m B.小于1.2m
C.等于1.2m D.小于或等于1.2m
8.如图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线
B.灯光光线
C.可能为太阳光线或灯光光线
D.该影子实际不可能存在
9.一个几何体的三视图如图所示,则这个几何体的体积为( )
A.24 B.24π C.96 D.96π
10.太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,则皮球的直径是( )
A. B.15 C.10 D.
11.画如图所示物体的主视图,正确的是( )
A. B.
C. D.
二.填空题(共10小题,满分30分)
12.如图是某天内,电线杆在不同时刻的影长,按先后顺序应当排列为 .
13.我们把大型会场、体育看台、电影院建为阶梯形状,是为了 .
14.请你写出一种几何体,使得它的主视图、左视图和俯视图都一样,它是 .
15.如图,直三棱柱ABC﹣A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为 .
16.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为 m.
17.如图,在常见的几何体圆锥、圆柱、球、长方体中,主视图与它的左视图一定完全相同的几何体有 (填编号).
18.如图是一个立体图形从左面和上面看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最少有 个.
19.小芳的房间有一面积为3m2的玻璃窗,她站在室内离窗子4m的地方向外看,她能看到窗前面一幢楼房的面积有 m2(楼之间的距离为20m).
20.如图,右边的图形是物体的 图.
21.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
三.解答题(共6小题,满分57分)
22.小明和小红并排站立在阳光下,小明身高1.75米,他的影长2.0米,小红比小明矮7厘米,此时小红的影长是多少米?
23.如图,楼房和旗杆在路灯下的影子如图所示.试确定路灯灯泡的位置,再作出小树在路灯下的影子.(不写作法,保留作图痕迹)
24.如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
25.如图①是一张长为18cm,宽为12cm的长方形硬纸板.把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积V= cm3;(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大?
x/cm 1 2 3 4 5
V/cm3 160 216 80
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出x的值;如果不是正方形,请说明理由.
26.有一个正方体,在它的各个面上分别标上数字1、2、3、4、5、6.小明、小刚、小红三人从不同的角度去观察此正方体,观察结果如图所示,问这个正方体各个面上的数字对面各是什么数字?
27.如图是某比赛场馆的平面图,根据距离比赛场地的远近和视角的不同,将观赛场地划分成A、B、C三个不同的票价区.其中与场地边缘MN的视角大于或等于45°,并且距场地边缘MN的距离不超过30m的区域划分为A票区,B票区如图所示,剩下的为C票区.(π取3)
(1)请你利用尺规作图,在观赛场地中,作出A票区所在的区域(只要作出图形,保留作图痕迹,不要求写作法);
(2)如果每个座位所占的平均面积是0.8平方米,请估算A票区有多少个座位.
参考答案与试题解析
一.选择题(共11小题,满分33分)
1.解:由图片可知,E视点的盲区应该在三角形ABD的区域内.
故选:D.
2.解:如图所示的几何体的从上面看到的形状图是.
故选:D.
3.解:A、圆柱的左视图是矩形,故本选项不符合题意;
B、三棱锥的左视图是三角形,故本选项符合题意;
C、三棱柱的左视图是矩形,故本选项不符合题意;
D、正方体的左视图是正方形,故本选项不符合题意.
故选:B.
4.解:几何体的主视图为.
故选:B.
5.解:因为圆柱的左视图是矩形,圆锥的左视图是等腰三角形,球的左视图是圆,正方体的左视图是正方形,
所以,左视图是圆的几何体是球.
故选:B.
6.解:A.俯视图与主视图都是正方形,故选项A不合题意;
B.俯视图是圆,主视图是长方形,故选项B合题意;
C.俯视图与主视图都是圆,故选项C不合题意;
D.俯视图和主视图是长方形;故选项D不符合题意;
故选:B.
7.解:正投影的长度与木棒的摆放角度有关系,但无论怎样摆都不会超过1.2 m.
故选:D.
8.解:若形成的影子是由太阳光照射形成的影子,则两直线一定平行;若形成的影子是由灯光照射而形成的影子,则两直线一定相交.所以可判断形成该影子的光线为灯光光线.故选:B.
9.解:由三视图确定该几何体是圆柱体,底面半径是4÷2=2,高是6,
则这个几何体的体积为π×22×6=24π.
故选:B.
10.解:由题意得:DC=2R,DE=10,∠CED=60°,
∴可得:DC=DEsin60°=15.
故选:B.
11.解:从正面看得到的图形是A.
故选:A.
二.填空题(共10小题,满分30分)
12.解:根据北半球上太阳光下的影子变化的规律,
从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.
可得顺序为DABC.
13.解:把大型会场、体育看台、电影院建为阶梯形状,是为了使后面的观众有更大的视野,从而减小盲区.
14.解:球的3个视图都为圆;
正方体的3个视图都为正方形;
所以主视图、左视图和俯视图都一样的几何体为球、正方体等.
15.解:此直三棱柱左视图是长为2,宽为AB边上的高的矩形,
∵底面各边长均为2,
∴△ABC是等边三角形,AB边上的高为2×=,
∴此直三棱柱左视图的面积=2×=2.
故答案为:2.
16.解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED FD,
代入数据可得DC2=16,
DC=4;
故答案为:4.
17.解:①圆锥主视图是三角形,左视图也是三角形,
②圆柱的主视图和左视图都是矩形;
③球的主视图和左视图都是圆形;
④长方体的主视图是矩形,左视图也是矩形,但是长和宽不一定相同,
故选:①②③.
18.解:根据俯视图可得:底层正方体最少5个正方体,
根据左视图可得:第二层最少有1个正方体;
则构成这个立体图形的小正方体的个数最少为5+1=6(个).
故答案为:6.
19.解:根据题意:她能看到窗前面一幢楼房的图形与玻璃窗的外形应该相似,且相似比为=6,
故面积的比为36;
故她能看到窗前面一幢楼房的面积有36×3=108(m2).
20.解:由三视图的概念,可得该图形的左视图是竖着的三个正方形;
俯视图是两排,下右侧由一个正方形,上面并排三个正方形;
所以右边的图形是物体的主视图.
21.解:(1)根据如图所示即可数出有11块小正方体;
(2)如图所示;左视图,俯视图分别如下图:
故答案为:(1)11.
三.解答题(共6小题,满分57分)
22.解:设小红的影长是x米,
根据题意得=,
解得x=1.92.
答:小红的影长是1.92米.
23.解:
24.解:作AD和BC的延长线交于点E,
设墙上的影高CD落在地面上时的长度为xm,树高为hm,
∵某一时刻测得长为1m的竹竿影长为0.9m,墙上的影高CD为1.2m,
∴,解得x=1.08(m),
∴树的影长为:1.08+2.7=3.78(m),
∴,解得h=4.2(m).
答:测得的树高为4.2米.
25.解:(1)由题意得,长方体盒子的长(18﹣2x)、宽(12﹣2x)、高x,因此体积为:(18﹣2x) (12﹣2x) x,
故答案为:(18﹣2x) (12﹣2x) x,
(2)把x=2代入(18﹣2x) (12﹣2x) x得,(18﹣2x) (12﹣2x) x=14×8×2=224,
把x=4代入(18﹣2x) (12﹣2x) x得,(18﹣2x) (12﹣2x) x=10×4×4=160,
故答案为:224,160;
(3)它的形状不可能是正方形,
当18﹣2x=x时,即x=6,而当x=6时,图①的长边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
26.解:从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5面,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
27.解:(1)如图,以线段MN、EF与、所围成的区域就是所作的A票区.
(2)连接OM、ON、OE、OF,设MN的中垂线与MN、EF分别相交于点G和H.
由题意,得∠MON=90°.
∵OG⊥MN,OH⊥EF,
OG=OH=15,
∴∠EOF=∠MON=90°.
∴.
∴SA=(S扇形FOM+S扇形EON)+(S△OMN+S△EOF)=πr2+r2≈1125(米2).
∴1125÷0.8≈1406.
∴A票区约有1406个座位.
