华东师大版数学七年级下册 10.5 图形的全等 课件(共15张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册 10.5 图形的全等 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 895.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 15:10:29 | ||
图片预览




文档简介
(共15张PPT)
第10章
轴对称、平移与旋转
10.5 图形的全等
1.理解全等图形的定义.
2.探究全等图形的性质与判定.(难点)
3.从全等图形的判定到全等三角形的判定.(重点)
学习目标
情境引入
思考:从这组图中,你看出了什么?
每组图形中的每个图形的形状、大小都一样
为什么?还有其
他的规律吗?
导入新课
全等图形的相关概念
一
观察与思考
讲授新课
知识要点
全等图形的定义:
能够完全重合的两个图形叫作全等图形.
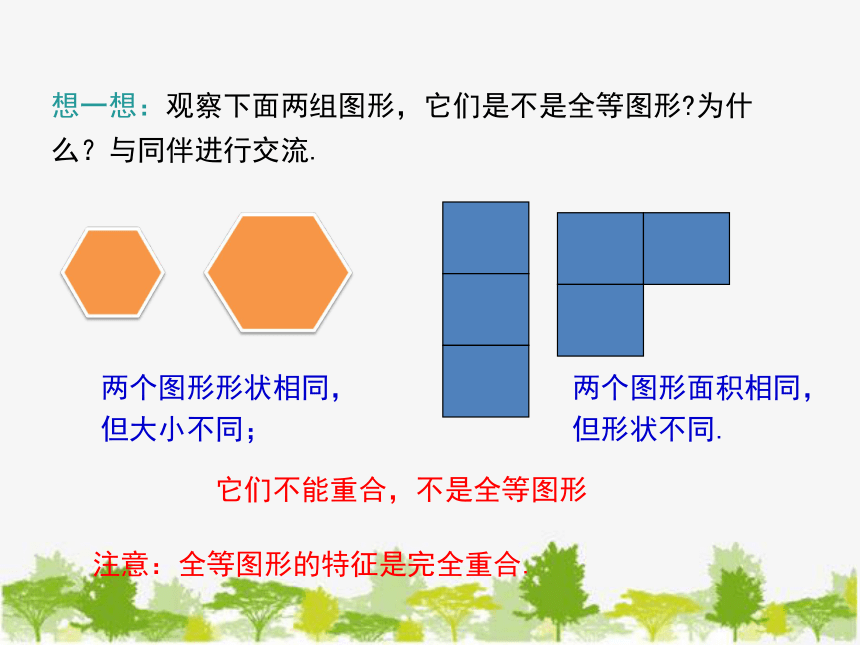
想一想:观察下面两组图形,它们是不是全等图形 为什
么?与同伴进行交流.
两个图形形状相同,但大小不同;
两个图形面积相同,但形状不同.
它们不能重合,不是全等图形
注意:全等图形的特征是完全重合.
问题:如果两个图形全等,它们的形状与大小一定相吗?
全等图形的形状与大小都相同.
知识要点
1.两个能够完全重合的图形称为全等图形.
2.图形经过翻折、旋转或平移这三种基本的变换,前后两个图形是全等图形.
3.两个全等图形经过翻折、旋转或平移这三种基本的变换后一定能够完全重合.
思考:观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?
概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫作对应顶点,相互重合的边叫作对应边,相互重合的角叫作对应角.
全等图形的性质
二
A
B
C
D
E
A1
B1
C1
D1
E1
五边形ABCDE 五边形A1B1C1D1E1
对应边
试一试:找出下面全等多边形的等量关系
AB A1B1
BC B1C1
CD C1D1
DE D1E1
EA E1A1
=
=
=
=
=
对应角
∠A ∠A1
∠B ∠B1
∠D = ∠D1
∠E ∠E1
=
=
=
∠C=∠C'
此符号表示全等,读作“全等于”.
全等多边形的性质:
全等多边形的对应边、对应角分别相等.
全等多边形的判定方法:
如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
全等三角形的性质:
全等三角形的对应边、对应角分别相等.
全等三角形的判定方法:
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
归纳总结
练一练:(1)如果△ABC ≌△DEF,那么你可以得到:
(2)如果具备:
∠A=∠D,∠B=∠E,∠C=∠F.
A
B
C
D
E
F
AB=DE,BC=EF,∠B=∠E
那么可以得出 △ABC ≌△DEF .
AB=DE,BC=EF,AC=DF;
A
B
C
D
E
F
例:如图,△ABC沿着BC的方向平移至 △DEF,∠A=80°, ∠B=60°,求∠F的度数.
解:
由图形平移的特征,可知△ABC与△DEF的形状和大小相同,即:
△ABC ≌△DEF
∴ ∠D=∠A=80 °
同理∠DEF= ∠B=60 °.
又∵ ∠D+∠DEF+∠F=180°
∴ ∠F=180 °- ∠D-∠DEF
=40°
典例精析
1.如图,已知△ ABC和△ DCB全等,AB和DC是对应边,BC是公共边,说出这两个全等三角形的其他对应边和对应角以及对应顶点.
B
D
A
C
对应边:AB对应DC,AC对应DB,BC对应CB
对应角:∠A对应∠D,∠ABC对应∠DCB,∠ACB对应DBC
对应顶点:A对应D,C对应B,B对应C
随堂练习
2.已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度.
解:∵ △ABC≌△DEF (已知) ∴AC=DF.(全等三角形的对应边等) ∵△ABC的周长是40cm, AB=10cm,BC=16cm, (已知) ∴ AC=40-10-16=14(cm), ∴ DF=14cm.
A
B
C
D
E
F
全等图形
概念
对应点、对应角、对应边
性质
对应角相等,对应边相等
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
课堂小结
第10章
轴对称、平移与旋转
10.5 图形的全等
1.理解全等图形的定义.
2.探究全等图形的性质与判定.(难点)
3.从全等图形的判定到全等三角形的判定.(重点)
学习目标
情境引入
思考:从这组图中,你看出了什么?
每组图形中的每个图形的形状、大小都一样
为什么?还有其
他的规律吗?
导入新课
全等图形的相关概念
一
观察与思考
讲授新课
知识要点
全等图形的定义:
能够完全重合的两个图形叫作全等图形.
想一想:观察下面两组图形,它们是不是全等图形 为什
么?与同伴进行交流.
两个图形形状相同,但大小不同;
两个图形面积相同,但形状不同.
它们不能重合,不是全等图形
注意:全等图形的特征是完全重合.
问题:如果两个图形全等,它们的形状与大小一定相吗?
全等图形的形状与大小都相同.
知识要点
1.两个能够完全重合的图形称为全等图形.
2.图形经过翻折、旋转或平移这三种基本的变换,前后两个图形是全等图形.
3.两个全等图形经过翻折、旋转或平移这三种基本的变换后一定能够完全重合.
思考:观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?
概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫作对应顶点,相互重合的边叫作对应边,相互重合的角叫作对应角.
全等图形的性质
二
A
B
C
D
E
A1
B1
C1
D1
E1
五边形ABCDE 五边形A1B1C1D1E1
对应边
试一试:找出下面全等多边形的等量关系
AB A1B1
BC B1C1
CD C1D1
DE D1E1
EA E1A1
=
=
=
=
=
对应角
∠A ∠A1
∠B ∠B1
∠D = ∠D1
∠E ∠E1
=
=
=
∠C=∠C'
此符号表示全等,读作“全等于”.
全等多边形的性质:
全等多边形的对应边、对应角分别相等.
全等多边形的判定方法:
如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
全等三角形的性质:
全等三角形的对应边、对应角分别相等.
全等三角形的判定方法:
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
归纳总结
练一练:(1)如果△ABC ≌△DEF,那么你可以得到:
(2)如果具备:
∠A=∠D,∠B=∠E,∠C=∠F.
A
B
C
D
E
F
AB=DE,BC=EF,∠B=∠E
那么可以得出 △ABC ≌△DEF .
AB=DE,BC=EF,AC=DF;
A
B
C
D
E
F
例:如图,△ABC沿着BC的方向平移至 △DEF,∠A=80°, ∠B=60°,求∠F的度数.
解:
由图形平移的特征,可知△ABC与△DEF的形状和大小相同,即:
△ABC ≌△DEF
∴ ∠D=∠A=80 °
同理∠DEF= ∠B=60 °.
又∵ ∠D+∠DEF+∠F=180°
∴ ∠F=180 °- ∠D-∠DEF
=40°
典例精析
1.如图,已知△ ABC和△ DCB全等,AB和DC是对应边,BC是公共边,说出这两个全等三角形的其他对应边和对应角以及对应顶点.
B
D
A
C
对应边:AB对应DC,AC对应DB,BC对应CB
对应角:∠A对应∠D,∠ABC对应∠DCB,∠ACB对应DBC
对应顶点:A对应D,C对应B,B对应C
随堂练习
2.已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度.
解:∵ △ABC≌△DEF (已知) ∴AC=DF.(全等三角形的对应边等) ∵△ABC的周长是40cm, AB=10cm,BC=16cm, (已知) ∴ AC=40-10-16=14(cm), ∴ DF=14cm.
A
B
C
D
E
F
全等图形
概念
对应点、对应角、对应边
性质
对应角相等,对应边相等
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
课堂小结
