3.2.1直线的点斜式方程
图片预览






文档简介
课件16张PPT。3.2.1《直线的点斜式方程》湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作2.过点A(x1,y1)、B (x2,y2)的直线的斜率k=_______温故而知新1.直线的倾斜角α与斜率k的关系是 __________3.简述在直角坐标系中确定一条直线的几何要素.(1)直线上的一点和直线的倾斜角(或斜率)
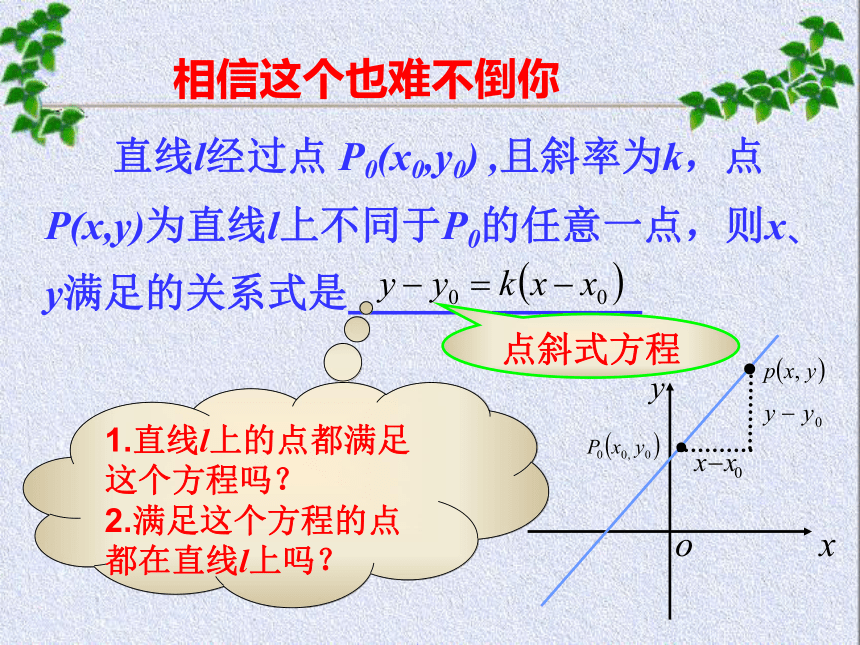
(2)直线上两点(α≠90°)试试自己的能耐 直线 l 过点P(2,1),且斜率为3,点Q(x,y)是 l 上不同于P的一点,则x、y满足怎样的关系式?相信这个也难不倒你 直线l经过点 P0(x0,y0) ,且斜率为k,点P(x,y)为直线l上不同于P0的任意一点,则x、y满足的关系式是_____________1.直线l上的点都满足这个方程吗?
2.满足这个方程的点都在直线l上吗?点斜式方程学会自己探究 直角坐标系上任意直线都可以用直线的点斜式方程表示吗?y-y0=0, 或 y=y0x-x0=0,或x=x0(1)当直线l的倾斜角为0°时, tan0 °=0,即k=0
这时直线l与x轴平行或重合,那么l的方程就是:(2)当直线l的倾斜角为90°时, 斜率不存在
这时直线l与y轴平行或重合,那么l的方程就是:所以:只要直线的斜率存在,直线就可以用点斜式方程来表示点斜式方程的应用:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2Oxy-55°P1°°练习你都作对了吗?直线的斜截式方程:已知直线l的斜率是k,与y轴的交点是P(0,b),求直线方程。代入点斜式方程,得l的直线方程:
y - b =k ( x - 0)即 y = k x + b 。(2) 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距。 方程(2)是由直线的斜率k与它在y轴上的截距b确定,所以方程(2)叫做直线的斜截式方程,简称斜截式。学习数学要善于发现问题 比较直线的点斜式方程:y-y0=k(x-x0)与一次函数解析式:y=kx+b,你有什么发现?斜截式方程:斜截式方程的应用:例2:斜率是5,在y轴上的截距是4的直线方程。解:由已知得k =5, b= 4,代入斜截式方程y= 5x + 4斜截式方程:y = k x + b 几何意义:k 是直线的斜率,b是直线在y轴上的截距自我巩固一下练习:写出下列直线的斜截式方程
(1)斜率为 ,在y轴上的截距为-2;
(2)斜率为-2,与y轴交于点(0,4)例题分析:∥练习判断下列各直线是否平行或垂直
(1)
(2)例4:求过点(1,2)且与两坐标轴组成一等腰直角
三角形的直线方程。
解:∵直线与坐标轴组成一等腰直角三角形 ∴k=±1直线过点(1,2)代入点斜式方程得y- 2 = x - 1 或y-2=-(x-1)即x-y+1=0或x+y-1=0例5:已知直线l过A(3,-5)和B(-2,5),求直
线l的方程解:∵直线l过点A(3,-5)和B(-2,5)将A(3,-5),k=-2代入点斜式,得y-(-5) =-2 ( x-3 ) ,即 2x + y -1 = 0①直线的点斜式,斜截式方程在直线斜率存在时才可以应用。
②直线方程的最后形式应表示成二元一次方程的一般形式。总结:斜截式方程:y = k x + b 几何意义:k 是直线的斜率,b是直线在y轴上的截距点斜式方程:y-y1=k(x-x1)直线L1:y = k 1x +b1,L2:y=k2x+b2
高中数学老师欧阳文丰制作2.过点A(x1,y1)、B (x2,y2)的直线的斜率k=_______温故而知新1.直线的倾斜角α与斜率k的关系是 __________3.简述在直角坐标系中确定一条直线的几何要素.(1)直线上的一点和直线的倾斜角(或斜率)
(2)直线上两点(α≠90°)试试自己的能耐 直线 l 过点P(2,1),且斜率为3,点Q(x,y)是 l 上不同于P的一点,则x、y满足怎样的关系式?相信这个也难不倒你 直线l经过点 P0(x0,y0) ,且斜率为k,点P(x,y)为直线l上不同于P0的任意一点,则x、y满足的关系式是_____________1.直线l上的点都满足这个方程吗?
2.满足这个方程的点都在直线l上吗?点斜式方程学会自己探究 直角坐标系上任意直线都可以用直线的点斜式方程表示吗?y-y0=0, 或 y=y0x-x0=0,或x=x0(1)当直线l的倾斜角为0°时, tan0 °=0,即k=0
这时直线l与x轴平行或重合,那么l的方程就是:(2)当直线l的倾斜角为90°时, 斜率不存在
这时直线l与y轴平行或重合,那么l的方程就是:所以:只要直线的斜率存在,直线就可以用点斜式方程来表示点斜式方程的应用:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2Oxy-55°P1°°练习你都作对了吗?直线的斜截式方程:已知直线l的斜率是k,与y轴的交点是P(0,b),求直线方程。代入点斜式方程,得l的直线方程:
y - b =k ( x - 0)即 y = k x + b 。(2) 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距。 方程(2)是由直线的斜率k与它在y轴上的截距b确定,所以方程(2)叫做直线的斜截式方程,简称斜截式。学习数学要善于发现问题 比较直线的点斜式方程:y-y0=k(x-x0)与一次函数解析式:y=kx+b,你有什么发现?斜截式方程:斜截式方程的应用:例2:斜率是5,在y轴上的截距是4的直线方程。解:由已知得k =5, b= 4,代入斜截式方程y= 5x + 4斜截式方程:y = k x + b 几何意义:k 是直线的斜率,b是直线在y轴上的截距自我巩固一下练习:写出下列直线的斜截式方程
(1)斜率为 ,在y轴上的截距为-2;
(2)斜率为-2,与y轴交于点(0,4)例题分析:∥练习判断下列各直线是否平行或垂直
(1)
(2)例4:求过点(1,2)且与两坐标轴组成一等腰直角
三角形的直线方程。
解:∵直线与坐标轴组成一等腰直角三角形 ∴k=±1直线过点(1,2)代入点斜式方程得y- 2 = x - 1 或y-2=-(x-1)即x-y+1=0或x+y-1=0例5:已知直线l过A(3,-5)和B(-2,5),求直
线l的方程解:∵直线l过点A(3,-5)和B(-2,5)将A(3,-5),k=-2代入点斜式,得y-(-5) =-2 ( x-3 ) ,即 2x + y -1 = 0①直线的点斜式,斜截式方程在直线斜率存在时才可以应用。
②直线方程的最后形式应表示成二元一次方程的一般形式。总结:斜截式方程:y = k x + b 几何意义:k 是直线的斜率,b是直线在y轴上的截距点斜式方程:y-y1=k(x-x1)直线L1:y = k 1x +b1,L2:y=k2x+b2
