华东师大版八年级下册数学 第18章平行四边形的复习 课件 (共14张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 第18章平行四边形的复习 课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 196.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
复习题
1. 能正确熟练地叙述平行四边形的性质和判定;
2. 能根据具体的问题情境选择适当的判定和性质,解决相关证明计算问题;
3. 能形成知识网络,选择简便方法解决相关证明计算问题。
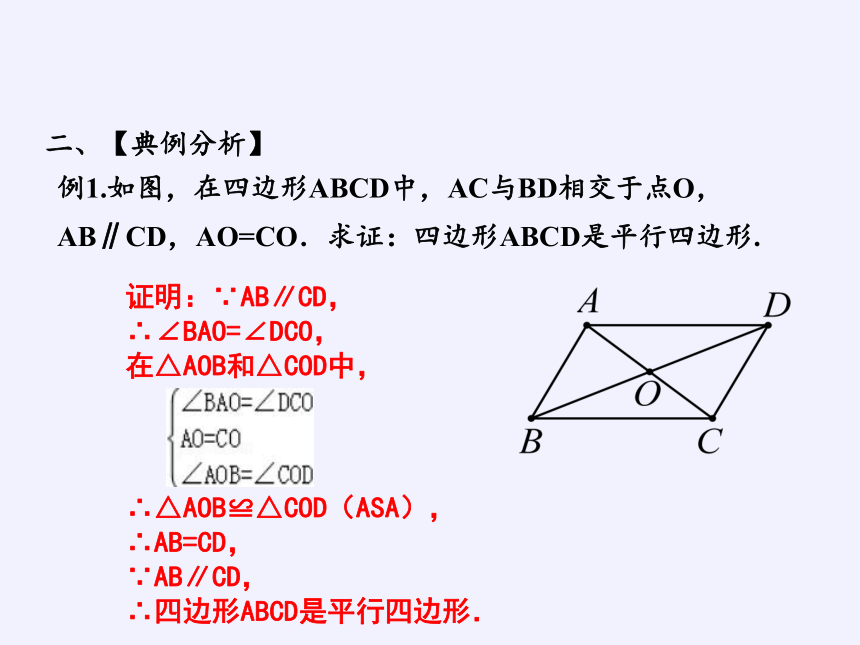
例1.如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,AO=CO.求证:四边形ABCD是平行四边形.
证明:∵AB∥CD,
∴∠BAO=∠DCO,
在△AOB和△COD中,
∴△AOB≌△COD(ASA),
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形.
二、【典例分析】
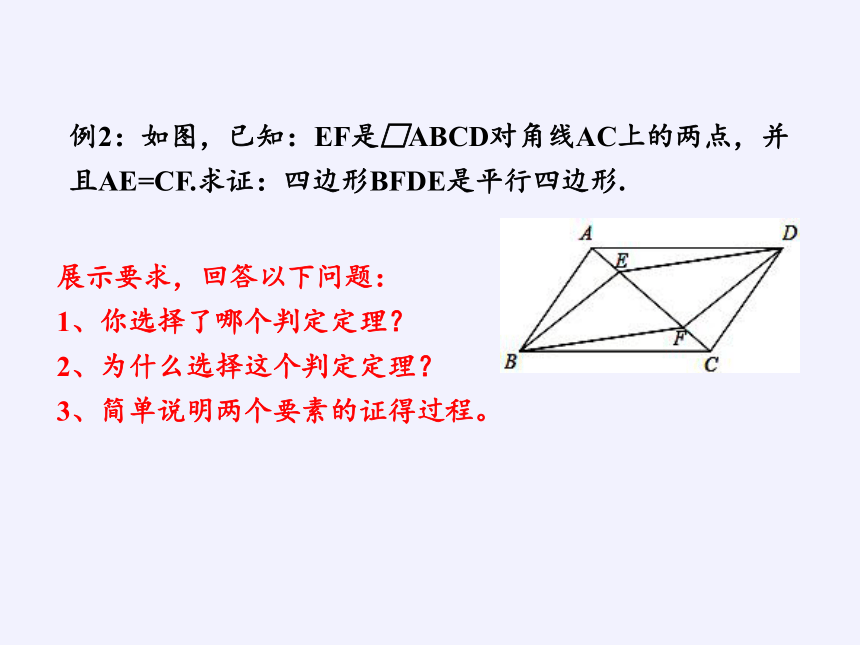
例2:如图,已知:EF是□ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
展示要求,回答以下问题:
1、你选择了哪个判定定理?
2、为什么选择这个判定定理?
3、简单说明两个要素的证得过程。
例2:如图,已知:EF是□ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形
∴OA=OC、OB=OD(平行四边形的对角线互相平分)
又∵AE=CF
∴OA﹣AE=OC﹣CF,即OE=OF
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
三、【变式巩固】
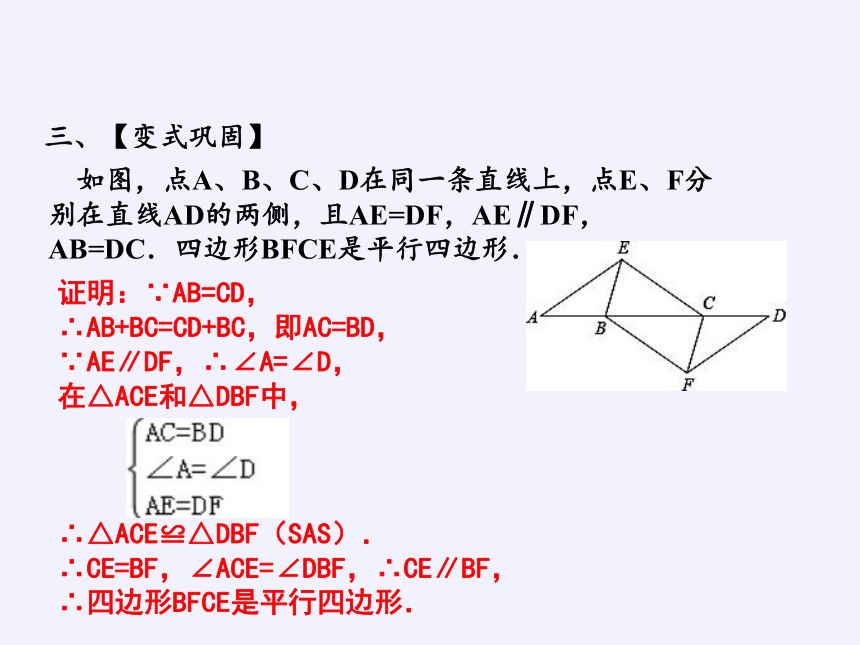
如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,AE∥DF,AB=DC.四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
∵AE∥DF,∴∠A=∠D,
在△ACE和△DBF中,
∴△ACE≌△DBF(SAS).
∴CE=BF,∠ACE=∠DBF,∴CE∥BF,
∴四边形BFCE是平行四边形.
四、【目标自测】
5.(目标1)已知□ABCD,∠BAD=40°,则∠BCD= °,∠ADC= °,对角线AC与BD相交于点O,若AC=10,则AO= .
6.如图,在□ABCD中,下列说法正确的是( )
A.AC=BD B.AC⊥BD
C.AB=CD D.AB=BC
5
40
140
C
7.如图,已知在四边形ABCD中,AB∥CD,请补充一个条件,使四边形ABCD是平行四边形. 你补充的条件是:
.
AB=CD
或AD∥BC
或OA=OC
或∠ABC=∠ADC
8.如图,在□ABCD中,点E,F分别为AB,CD的中点,求证四边形EBCF为平行四边形.
证明:在□ABCD中,
BC=DA,∠B=∠D,AB=CD,
又∵E,F分别为AB,CD的中点,
∴BE=DF.
在△AFD和△CEB中,
∴△AFD≌△CEB(SAS)
∴FC=AE
又∵FC∥AE
∴四边形AECF为平行四边形.
9.如图,在四边形ABCD中,AD∥BC且AD>BC,BC=12,蚂蚁P从点A出发,以1cm/s的速度向点D运动,蚂蚁Q从点C出发,以2cm/s的速度向点B运动,几秒钟后四边形APQB恰好为平行四边形?
五、【反思提高】
解:设点P由A向D运动t秒,则AP=tcm,CQ=2tcm.
∵BC=12,∴BQ=12﹣2t,
当AP∥BQ且AP=BQ时四边形ABQP为平行四边形,
∴12﹣2t=t,解得:t=4,
∴4s后四边形ABQP成为平行四边形.
性质:
边角关系
转化
判定:
边角关系
转化
类似:
互逆
角平分线性质
中垂线性质
谢 谢
复习题
1. 能正确熟练地叙述平行四边形的性质和判定;
2. 能根据具体的问题情境选择适当的判定和性质,解决相关证明计算问题;
3. 能形成知识网络,选择简便方法解决相关证明计算问题。
例1.如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,AO=CO.求证:四边形ABCD是平行四边形.
证明:∵AB∥CD,
∴∠BAO=∠DCO,
在△AOB和△COD中,
∴△AOB≌△COD(ASA),
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形.
二、【典例分析】
例2:如图,已知:EF是□ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
展示要求,回答以下问题:
1、你选择了哪个判定定理?
2、为什么选择这个判定定理?
3、简单说明两个要素的证得过程。
例2:如图,已知:EF是□ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形
∴OA=OC、OB=OD(平行四边形的对角线互相平分)
又∵AE=CF
∴OA﹣AE=OC﹣CF,即OE=OF
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
三、【变式巩固】
如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,AE∥DF,AB=DC.四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
∵AE∥DF,∴∠A=∠D,
在△ACE和△DBF中,
∴△ACE≌△DBF(SAS).
∴CE=BF,∠ACE=∠DBF,∴CE∥BF,
∴四边形BFCE是平行四边形.
四、【目标自测】
5.(目标1)已知□ABCD,∠BAD=40°,则∠BCD= °,∠ADC= °,对角线AC与BD相交于点O,若AC=10,则AO= .
6.如图,在□ABCD中,下列说法正确的是( )
A.AC=BD B.AC⊥BD
C.AB=CD D.AB=BC
5
40
140
C
7.如图,已知在四边形ABCD中,AB∥CD,请补充一个条件,使四边形ABCD是平行四边形. 你补充的条件是:
.
AB=CD
或AD∥BC
或OA=OC
或∠ABC=∠ADC
8.如图,在□ABCD中,点E,F分别为AB,CD的中点,求证四边形EBCF为平行四边形.
证明:在□ABCD中,
BC=DA,∠B=∠D,AB=CD,
又∵E,F分别为AB,CD的中点,
∴BE=DF.
在△AFD和△CEB中,
∴△AFD≌△CEB(SAS)
∴FC=AE
又∵FC∥AE
∴四边形AECF为平行四边形.
9.如图,在四边形ABCD中,AD∥BC且AD>BC,BC=12,蚂蚁P从点A出发,以1cm/s的速度向点D运动,蚂蚁Q从点C出发,以2cm/s的速度向点B运动,几秒钟后四边形APQB恰好为平行四边形?
五、【反思提高】
解:设点P由A向D运动t秒,则AP=tcm,CQ=2tcm.
∵BC=12,∴BQ=12﹣2t,
当AP∥BQ且AP=BQ时四边形ABQP为平行四边形,
∴12﹣2t=t,解得:t=4,
∴4s后四边形ABQP成为平行四边形.
性质:
边角关系
转化
判定:
边角关系
转化
类似:
互逆
角平分线性质
中垂线性质
谢 谢
