华东师大版八年级下册数学 17.3.2 一次函数的图象 课件(共26张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 17.3.2 一次函数的图象 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 15:39:19 | ||
图片预览







文档简介
(共26张PPT)
一次函数的图象
学习目标
这是神马东西?
平面直角坐标系
A
第一象限
B
第二象限
C
第三象限
D
第四象限
探究在线一:
(1)当K>0时,正比例函数图像
经过 ____、____象限
(2)当K<0时,正比例函数图像
经过 ____、____象限
一
三
二
四
观察右图图像,回答问题:
1、图中的直线都是谁的函数图像?
正比例函数图像
正比例函数的图象是经过原点(___,___)的一条直线。
2、为什么?
3、直线的象限分布规律:
0
0
B
学以致用:
2、正比例函数y=0.5x的图像经过___、___象限
3、正比例函数y=(m-2)x的图像经过一、三象限,则m的取值范围是________
一
三
m>2
4、正比例函数y=(a-1)xa -1的图像经过二、四象限,则a的取值是________
a=-2
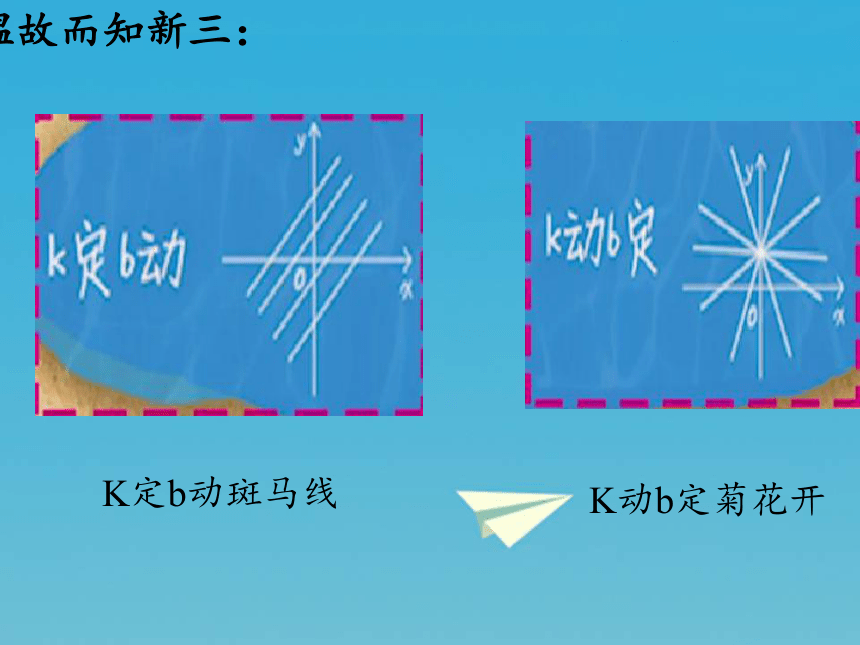
温故而知新三:
K定b动斑马线
K动b定菊花开
详细的说:
如果在直线y=k1x+b1和直线y=k2x+b2中,如果k1=k2,那么这两条直线________,如果b1 = b2 ,那么,这两条直线会与y轴相交于_________。
相互平行
同一点
我们知道两直线的k值相等时,这两条直线________,其实其中一条直线可以看作是由另一条直线平移得到,那怎样平移的呢?让我们一起来观察一个小动画吧?
直线的平移演示.gsp
探究在线二:
相互平行
总结:
当b值为正的时候向___移b个单位,交与y轴的正半轴。当b值为负的时候向___移 b 个单位,交与y轴的负半轴。
上加下减只变b
一次函数的上下平移口诀:
上
下
小试牛刀:
⑴ 将直线y=3x向下平移2个单位,得到直线________。
⑵ 将直线y=﹣x ﹣5向上平移5个单位,得到直线_____。
y=3x ﹣2
y= ﹣ x
探究在线三:
请结合正比例函数图像象限分布规律和平移规律
说出直线y=2x+3经过的象限?____________
你的推理是:___________________________
直线y=-2x+3经过_________象限
按照你的推理请分别说出:
直线y=2x-3经过_________象限
直线y=-2x-3经过_________象限
请在坐标系中分别画出:
并读出它们经过的象限, 对照推理是否一致?
小组交流合作:
分别画出y=kx+b(k≠0 ,b≠0)
四种情况的草图:
一次函数y=kx+b中的k与b的正负与它的图像经过的象限归纳列表如下:
(二)
(一)
k<0 b>0
k<0 b<0
k>0 b>0
k>0 b<0
(三)
(四)
活学活用:
观察下列一次函数y=kx+b的草图,你能说出k和b的符号吗?
k,b的符号可以确定直线y=kx+b的位置,反过来由直线y=kx+b的位置可以确定k,b的符号.
总结:
1、关于一次函数y=2x-1的图象,下列说法正确的是( )
A.图象经过第一、二、三象限
B.图象经过第一、三、四象限
C.图象经过第一、二、四象限
D.图象经过第二、三、四象限
趁热打铁:
B
3、如果直线y=(m-2)x+(m-1)经过第一、二、四象限,则实数m的取值范围是( )
A.m<2 B.m>1 C.m≠2 D.12、已知一次函数的图象如右图所示,则 ( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
C
D
4、正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )
B
5、如果一次函数y=kx+b的图象不经过第三象限,那么k,b的取值范围是( )
A.K<0且b>0 B.k>0且b ≤ 0
C.k<0且b≥0 D.k<0且b<0
C
6、如果直线 y=3x+b 与 y轴交点的纵坐标为 -2,那么这条直线一定不经过第 ( )象限.
A.二 B.三 C.一、 D.四
A
1、正比例函数y=kx图像与K、b的关系:
k>0 过一、三象限
k<0 过二、四象限
2、平移规律:上加下减只变b
3、一次函数y=kx+b图像与K、b的关系:
b>0 过一、二、三象限
k>0
b<0 过一、三、四象限
b>0 过一、二、四象限
k<0
b<0 过二、三、四象限
4、k,b的符号可以确定直线y=kx+b的位置,反过来由直线y=kx+b的位置可以确定k,b的符号.
课堂小结
886
一种花,圆脸盘;
高高个儿黄帽檐。
早朝东来晚朝西;
笑脸迎着太阳转
谢 谢
一次函数的图象
学习目标
这是神马东西?
平面直角坐标系
A
第一象限
B
第二象限
C
第三象限
D
第四象限
探究在线一:
(1)当K>0时,正比例函数图像
经过 ____、____象限
(2)当K<0时,正比例函数图像
经过 ____、____象限
一
三
二
四
观察右图图像,回答问题:
1、图中的直线都是谁的函数图像?
正比例函数图像
正比例函数的图象是经过原点(___,___)的一条直线。
2、为什么?
3、直线的象限分布规律:
0
0
B
学以致用:
2、正比例函数y=0.5x的图像经过___、___象限
3、正比例函数y=(m-2)x的图像经过一、三象限,则m的取值范围是________
一
三
m>2
4、正比例函数y=(a-1)xa -1的图像经过二、四象限,则a的取值是________
a=-2
温故而知新三:
K定b动斑马线
K动b定菊花开
详细的说:
如果在直线y=k1x+b1和直线y=k2x+b2中,如果k1=k2,那么这两条直线________,如果b1 = b2 ,那么,这两条直线会与y轴相交于_________。
相互平行
同一点
我们知道两直线的k值相等时,这两条直线________,其实其中一条直线可以看作是由另一条直线平移得到,那怎样平移的呢?让我们一起来观察一个小动画吧?
直线的平移演示.gsp
探究在线二:
相互平行
总结:
当b值为正的时候向___移b个单位,交与y轴的正半轴。当b值为负的时候向___移 b 个单位,交与y轴的负半轴。
上加下减只变b
一次函数的上下平移口诀:
上
下
小试牛刀:
⑴ 将直线y=3x向下平移2个单位,得到直线________。
⑵ 将直线y=﹣x ﹣5向上平移5个单位,得到直线_____。
y=3x ﹣2
y= ﹣ x
探究在线三:
请结合正比例函数图像象限分布规律和平移规律
说出直线y=2x+3经过的象限?____________
你的推理是:___________________________
直线y=-2x+3经过_________象限
按照你的推理请分别说出:
直线y=2x-3经过_________象限
直线y=-2x-3经过_________象限
请在坐标系中分别画出:
并读出它们经过的象限, 对照推理是否一致?
小组交流合作:
分别画出y=kx+b(k≠0 ,b≠0)
四种情况的草图:
一次函数y=kx+b中的k与b的正负与它的图像经过的象限归纳列表如下:
(二)
(一)
k<0 b>0
k<0 b<0
k>0 b>0
k>0 b<0
(三)
(四)
活学活用:
观察下列一次函数y=kx+b的草图,你能说出k和b的符号吗?
k,b的符号可以确定直线y=kx+b的位置,反过来由直线y=kx+b的位置可以确定k,b的符号.
总结:
1、关于一次函数y=2x-1的图象,下列说法正确的是( )
A.图象经过第一、二、三象限
B.图象经过第一、三、四象限
C.图象经过第一、二、四象限
D.图象经过第二、三、四象限
趁热打铁:
B
3、如果直线y=(m-2)x+(m-1)经过第一、二、四象限,则实数m的取值范围是( )
A.m<2 B.m>1 C.m≠2 D.1
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
C
D
4、正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )
B
5、如果一次函数y=kx+b的图象不经过第三象限,那么k,b的取值范围是( )
A.K<0且b>0 B.k>0且b ≤ 0
C.k<0且b≥0 D.k<0且b<0
C
6、如果直线 y=3x+b 与 y轴交点的纵坐标为 -2,那么这条直线一定不经过第 ( )象限.
A.二 B.三 C.一、 D.四
A
1、正比例函数y=kx图像与K、b的关系:
k>0 过一、三象限
k<0 过二、四象限
2、平移规律:上加下减只变b
3、一次函数y=kx+b图像与K、b的关系:
b>0 过一、二、三象限
k>0
b<0 过一、三、四象限
b>0 过一、二、四象限
k<0
b<0 过二、三、四象限
4、k,b的符号可以确定直线y=kx+b的位置,反过来由直线y=kx+b的位置可以确定k,b的符号.
课堂小结
886
一种花,圆脸盘;
高高个儿黄帽檐。
早朝东来晚朝西;
笑脸迎着太阳转
谢 谢
