2020-2021学年北师大版七年级数学下册第四章三角形 同步测试(Word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第四章三角形 同步测试(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 168.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 16:45:29 | ||
图片预览



文档简介
北师大版七年级数学下册第四章三角形 同步测试
一.选择题
1.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
3.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则S△ABC的面积为( )
A. B.3 C. D.4
4.下列说法:①同位角相等;②任意三角形的三条中线交于一点;③钝角三角形只有一条高;④三角形的两边长分别为6和9,则这个三角形的第三边长不可能为16;⑤面积相等的两个三角形是全等图形;⑥两个直角一定互补.其中,正确的有( )
A.4个 B.3个 C.2个 D.1个
5.三角形的重心在( )
A.三角形的内部 B.三角形的外部
C.三角形的边上 D.要根据三角形的形状确定
6.如图,把一副三角板的两个直角三角形叠放在一起,则α的度数( )
A.75° B.135° C.120° D.105°
7.在下列条件中:①∠A=∠C﹣∠B,②∠A:∠B:∠C=2:3:5,③∠A=90°﹣∠B,④∠B﹣∠C=90°中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
8.下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
9.下列说法正确的是( )
A.两个等边三角形一定是全等图形 B.两个全等图形面积一定相等
C.形状相同的两个图形一定全等 D.两个正方形一定是全等图形
10.如图,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是( )
A.∠A=∠D,∠B=∠E B.AC=DF,AB=DE
C.∠A=∠D,AB=DE D.AC=DF,CB=FE
11.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
A.SSS B.SAS C.ASA D.AAS
12.如果将长度为a-2、a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是( )
A. a>-1 B. a>2 C. a>5 D. 无法确定
二.填空题
13.如图,图中以BC为边的三角形的个数为 .
14.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上 根木条.
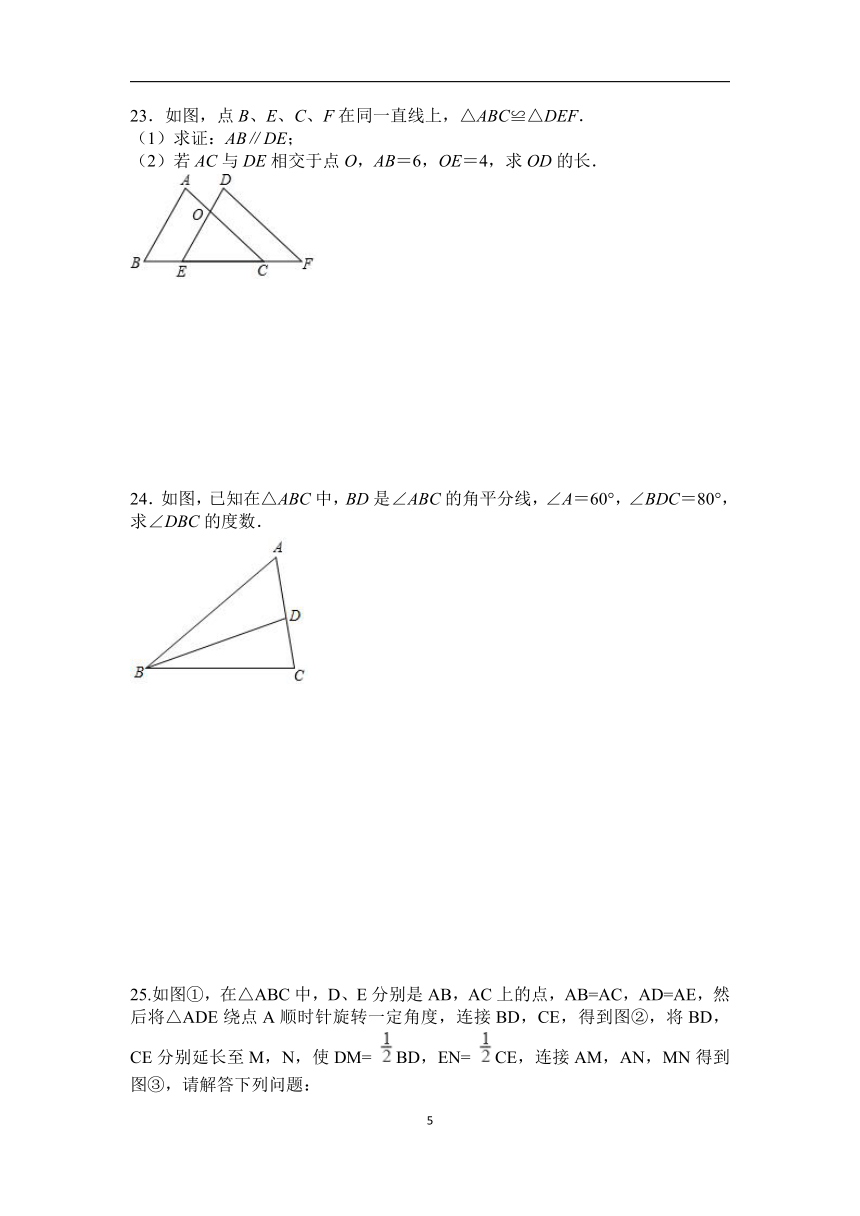
15.已知△ABC的两条边长分别为2和5,则第三边c的取值范围是 .
16.如图,图中由实线围成的图形与①是全等形的有 .(填序号)
17.如图,已知AB=CD,只需再添一个条件就可以证明△ABC≌△CDA的是 .
18.如图,在四边形ABCD中,AB=CB,AD=CD.若∠A=108°,则∠C的大小=________(度).
故答案为:108
三.解答题
19.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上,三角形BDE与四边形ACDE的周长相等.
(1)求线段AE的长.
(2)若图中所有线段长度的和是53cm,求BC+DE的值.
20.如图,点E、C、D、A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.
求证:BC=EF.
21.若a,b,c是△ABC三边的长,化简:|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a﹣b|.
22.人教版初中数学教科书八年级上册第84页探究了“三角形中边与角之间的不等关系”,部分原文如图.
(1)请证明文中的∠ADE>∠B
(2)如图2,在△ABC中,如果∠ACB>∠B,能否证明AB>AC?
小敏同学提供了一种方法:将△ABC折叠,使点B落在点C上,折痕交AB于点F,交BC于点G,再运用三角形三边关系即可证明,请你按照小敏的方法完成证明.
23.如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
24.如图,已知在△ABC中,BD是∠ABC的角平分线,∠A=60°,∠BDC=80°,求∠DBC的度数.
25.如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= BD,EN= CE,连接AM,AN,MN得到图③,请解答下列问题:
(1)在图②中,BD与CE的数量关系是________;
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.
北师大版七年级数学下册第四章三角形 答案提示
一.选择题
1.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
解:三角形根据边分类 ,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
解:一个三角形的三条高的交点恰是三角形的一个顶点,这个三角形是直角三角形.
故选:C.
3.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则S△ABC的面积为( )
A. B.3 C. D.4
解:S△ABC=3×3﹣×=.
故选:C.
4.下列说法:
①同位角相等;②任意三角形的三条中线交于一点;③钝角三角形只有一条高;④三角形的两边长分别为6和9,则这个三角形的第三边长不可能为16;⑤面积相等的两个三角形是全等图形;⑥两个直角一定互补.其中,正确的有( )
A.4个 B.3个 C.2个 D.1个
解:如果两条平行直线被第三条直线所截,那么同位角相等,如果两条不平行直线被第三条直线所截,那么同位角不相等,故①错误;
任意三角形的三条中线交于一点,故②正确;
钝角三角形有三条高,故③错误;
三角形的两边长分别为6和9,则这个三角形的第三边长的取值范围是大于3且小于15,故④正确;
面积相等的两个三角形不一定是全等图形,故⑤错误;
两个直角一定互补,故⑥正确;
故选:B.
5.三角形的重心在( )
A.三角形的内部 B.三角形的外部
C.三角形的边上 D.要根据三角形的形状确定
解:∵三角形的重心是三角形三边中线的交点,
∴三角形的重心在三角形内部.
故选:A.
6.如图,把一副三角板的两个直角三角形叠放在一起,则α的度数( )
A.75° B.135° C.120° D.105°
解:∵图中是一副直角三角板,
∴∠1=45°,∠2=30°,
∴∠α=180°﹣45°﹣30°=105°.
故选:D.
7.在下列条件中:①∠A=∠C﹣∠B,②∠A:∠B:∠C=2:3:5,③∠A=90°﹣∠B,④∠B﹣∠C=90°中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
解:①因为∠A+∠B=∠C,则2∠C=180°,∠C=90°,所以△ABC是直角三角形;
②因为∠A:∠B:∠C=2:3:5,设∠A=2x,则2x+3x+5x=180,x=18°,∠C=18°×5=90°,所以△ABC是直角三角形;
③因为∠A=90°﹣∠B,所以∠A+∠B=90°,则∠C=180°﹣90°=90°,所以△ABC是直角三角形;
④因为∠B﹣∠C=90°,则∠B=90°+∠C,所以三角形为钝角三角形.
所以能确定△ABC是直角三角形的有①②③.
故选:C.
8.下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
解:A、两个图形不能完全重合,故本选项错误;
B、两个图形能够完全重合,故本选项正确;
C、两个图形不能完全重合,故本选项错误;
D、两个图形不能完全重合,故本选项错误;
故选:B.
9.下列说法正确的是( )
A.两个等边三角形一定是全等图形 B.两个全等图形面积一定相等
C.形状相同的两个图形一定全等 D.两个正方形一定是全等图形
解:A、两个等边三角形相似但不一定全等,故说法错误,不符合题意;
B、两个全等图形的面积一定相等,正确,符合题意;
C、形状相同的两个图形相似但不一定全等,故说法错误,不符合题意;
D、两个正方形相似但不一定全等,故说法错误,不符合题意,
故选:B.
10.如图,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是( )
A.∠A=∠D,∠B=∠E B.AC=DF,AB=DE
C.∠A=∠D,AB=DE D.AC=DF,CB=FE
解:A.添加条件∠A=∠D,∠B=∠E时,没有边的条件,故不能判定△ABC≌△DEF,
B.添加条件AC=DF,AB=DE,根据HL可证明△ABC≌△DEF,
C.添加条件∠A=∠D,AB=DE,根据AAS可证明△ABC≌△DEF,
D.添加条件AC=DF,CB=FE,根据SAS可证明△ABC≌△DEF,
故选:A.
11.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
A.SSS B.SAS C.ASA D.AAS
解:如图,连接AB、CD,
在△ABO和△DCO中,,
∴△ABO≌△DCO(SAS),
∴AB=CD.
故选:B.
12.如果将长度为a-2、a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是( )
A. a>-1 B. a>2 C. a>5 D. 无法确定
解:因为-2<2<5,
所以a-2<a+2<a+5,
所以由三角形三边关系可得a-2+a+2>a+5,
解得a>5.
则不等式的解集是a>5.
故选C.
二.填空题
13.如图,图中以BC为边的三角形的个数为 4 .
解:∵以BC为公共边的三角形有△BCD,△BCE,△BCF,△ABC,
∴以BC为公共边的三角形的个数是4个.
故答案为:4.
14.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上 3 根木条.
解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
故答案为:3.
15.已知△ABC的两条边长分别为2和5,则第三边c的取值范围是 3<c<7 .
解:由题意,得
5﹣2<c<5+2,
即3<c<7.
故答案为:3<c<7.
16.如图,图中由实线围成的图形与①是全等形的有 ②③ .(填序号)
解:由图可知,图上由实线围成的图形与①是全等形的有②,③,
故答案为:②③.
17.如图,已知AB=CD,只需再添一个条件就可以证明△ABC≌△CDA的是 AD .
A.BC=AD B.AD∥BC
C.∠B=∠D D.AB∥DC
解:A.根据BC=AD、AB=CD和AC=AC能推出△ABC≌△CDA(SSS);
B.∵AD∥BC,∴∠DAC=∠BCA,
∴根据AB=CD、AC=AC和∠BCA=∠DAC不能推出△ABC≌△CDA;
C.根据AB=CD,AC=AC和∠B=∠D不能推出△ABC≌△CDA;
D.∵AB∥DC,∴∠BAC=∠DCA,
根据AB=CD,∠BAC=∠DCA和AC=AC能推出△ABC≌△CDA(SAS);
故答案为:AD.
18.如图,在四边形ABCD中,AB=CB,AD=CD.若∠A=108°,则∠C的大小=________(度).
18.证明:连接BD,
∵在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),
∴∠C=∠A=108°,
故答案为:108
三.解答题
19.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上,三角形BDE与四边形ACDE的周长相等.
(1)求线段AE的长.
(2)若图中所有线段长度的和是53cm,求BC+DE的值.
解:(1)∵三角形BDE与四边形ACDE的周长相等,
∴BD+DE+BE=AC+AE+CD+DE,
∵BD=DC,
∴BE=AE+AC,
设AE=x cm,则BE=(10﹣x)cm,
由题意得,10﹣x=x+6.
解得,x=2,
∴AE=2cm;
(2)图中共有8条线段,
它们的和为:AE+EB+AB+AC+DE+BD+CD+BC=2AB+AC+2BC+DE,
由题意得,2AB+AC+2BC+DE=53,
∴2BC+DE=53﹣(2AB+AC)=53﹣(2×10+6)=27,
∴BC+DE=(cm).
20.如图,点E、C、D、A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.
求证:BC=EF.
证明:∵AB//DF,∴∠B=∠CPD,∠A=∠FDE,∵∠E=∠CPD,∴∠E=∠B,
在△ABC和△DEF中, , ∴△ABC △DEF(ASA), ∴BC=EF.
21.若a,b,c是△ABC三边的长,化简:|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a﹣b|.
解:∵a、b、c是△ABC的三边的长,
∴a+b﹣c>0,b﹣a﹣c<0,c﹣a﹣b<0,
∴原式=a+b﹣c﹣b+a+c+c﹣a﹣b=a﹣b+c.
22.人教版初中数学教科书八年级上册第84页探究了“三角形中边与角之间的不等关系”,部分原文如图.
(1)请证明文中的∠ADE>∠B
(2)如图2,在△ABC中,如果∠ACB>∠B,能否证明AB>AC?
小敏同学提供了一种方法:将△ABC折叠,使点B落在点C上,折痕交AB于点F,交BC于点G,再运用三角形三边关系即可证明,请你按照小敏的方法完成证明.
解:(1)∵∠ADE是△EBD的一个外角,∠B为与∠ADE不相邻的内角.
∴∠ADE>∠B.
(2)证明:∵将△ABC折叠,使点B落在点C上,
∴BF=CF,
在△ACF中,AF+FC>AC,即AF+BF>AC,
∴AB>AC.
23.如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE;
(2)解:∵△ABC≌△DEF,
∴AB=DE=6,
∵OE=4,
∴OD=DE﹣OE=6﹣4=2.
24.如图,已知在△ABC中,BD是∠ABC的角平分线,∠A=60°,∠BDC=80°,求∠DBC的度数.
解:∵∠A=60°,∠BDC=80°,
∴∠ABD=∠BDC﹣∠A=80°﹣60°=20°.
又∵BD是∠ABC的角平分线,
∴∠DBC=∠ABD=20°.
25.如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= BD,EN= CE,连接AM,AN,MN得到图③,请解答下列问题:
(1)在图②中,BD与CE的数量关系是________;
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.
解:(1)BD=CE
(2)解:AM=AN,∠MAN=∠BAC
∵ ∠DAE=∠BAC
∴ ∠CAE=∠BAD
在△BAD和△CAE中,
∴ △CAE≌△BAD(SAS)
∴ ∠ACE=∠ABD ,CE=BD
∵ DM= BD,EN= CE,BD=CE,
∴ BM=CN
在△ABM和△ACN中,
∴ △ABM≌△ACN(SAS)
∴ AM=AN, ∠BAM=∠CAN,∴∠MAN=∠BAC.
一.选择题
1.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
3.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则S△ABC的面积为( )
A. B.3 C. D.4
4.下列说法:①同位角相等;②任意三角形的三条中线交于一点;③钝角三角形只有一条高;④三角形的两边长分别为6和9,则这个三角形的第三边长不可能为16;⑤面积相等的两个三角形是全等图形;⑥两个直角一定互补.其中,正确的有( )
A.4个 B.3个 C.2个 D.1个
5.三角形的重心在( )
A.三角形的内部 B.三角形的外部
C.三角形的边上 D.要根据三角形的形状确定
6.如图,把一副三角板的两个直角三角形叠放在一起,则α的度数( )
A.75° B.135° C.120° D.105°
7.在下列条件中:①∠A=∠C﹣∠B,②∠A:∠B:∠C=2:3:5,③∠A=90°﹣∠B,④∠B﹣∠C=90°中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
8.下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
9.下列说法正确的是( )
A.两个等边三角形一定是全等图形 B.两个全等图形面积一定相等
C.形状相同的两个图形一定全等 D.两个正方形一定是全等图形
10.如图,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是( )
A.∠A=∠D,∠B=∠E B.AC=DF,AB=DE
C.∠A=∠D,AB=DE D.AC=DF,CB=FE
11.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
A.SSS B.SAS C.ASA D.AAS
12.如果将长度为a-2、a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是( )
A. a>-1 B. a>2 C. a>5 D. 无法确定
二.填空题
13.如图,图中以BC为边的三角形的个数为 .
14.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上 根木条.
15.已知△ABC的两条边长分别为2和5,则第三边c的取值范围是 .
16.如图,图中由实线围成的图形与①是全等形的有 .(填序号)
17.如图,已知AB=CD,只需再添一个条件就可以证明△ABC≌△CDA的是 .
18.如图,在四边形ABCD中,AB=CB,AD=CD.若∠A=108°,则∠C的大小=________(度).
故答案为:108
三.解答题
19.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上,三角形BDE与四边形ACDE的周长相等.
(1)求线段AE的长.
(2)若图中所有线段长度的和是53cm,求BC+DE的值.
20.如图,点E、C、D、A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.
求证:BC=EF.
21.若a,b,c是△ABC三边的长,化简:|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a﹣b|.
22.人教版初中数学教科书八年级上册第84页探究了“三角形中边与角之间的不等关系”,部分原文如图.
(1)请证明文中的∠ADE>∠B
(2)如图2,在△ABC中,如果∠ACB>∠B,能否证明AB>AC?
小敏同学提供了一种方法:将△ABC折叠,使点B落在点C上,折痕交AB于点F,交BC于点G,再运用三角形三边关系即可证明,请你按照小敏的方法完成证明.
23.如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
24.如图,已知在△ABC中,BD是∠ABC的角平分线,∠A=60°,∠BDC=80°,求∠DBC的度数.
25.如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= BD,EN= CE,连接AM,AN,MN得到图③,请解答下列问题:
(1)在图②中,BD与CE的数量关系是________;
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.
北师大版七年级数学下册第四章三角形 答案提示
一.选择题
1.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
解:三角形根据边分类 ,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
解:一个三角形的三条高的交点恰是三角形的一个顶点,这个三角形是直角三角形.
故选:C.
3.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则S△ABC的面积为( )
A. B.3 C. D.4
解:S△ABC=3×3﹣×=.
故选:C.
4.下列说法:
①同位角相等;②任意三角形的三条中线交于一点;③钝角三角形只有一条高;④三角形的两边长分别为6和9,则这个三角形的第三边长不可能为16;⑤面积相等的两个三角形是全等图形;⑥两个直角一定互补.其中,正确的有( )
A.4个 B.3个 C.2个 D.1个
解:如果两条平行直线被第三条直线所截,那么同位角相等,如果两条不平行直线被第三条直线所截,那么同位角不相等,故①错误;
任意三角形的三条中线交于一点,故②正确;
钝角三角形有三条高,故③错误;
三角形的两边长分别为6和9,则这个三角形的第三边长的取值范围是大于3且小于15,故④正确;
面积相等的两个三角形不一定是全等图形,故⑤错误;
两个直角一定互补,故⑥正确;
故选:B.
5.三角形的重心在( )
A.三角形的内部 B.三角形的外部
C.三角形的边上 D.要根据三角形的形状确定
解:∵三角形的重心是三角形三边中线的交点,
∴三角形的重心在三角形内部.
故选:A.
6.如图,把一副三角板的两个直角三角形叠放在一起,则α的度数( )
A.75° B.135° C.120° D.105°
解:∵图中是一副直角三角板,
∴∠1=45°,∠2=30°,
∴∠α=180°﹣45°﹣30°=105°.
故选:D.
7.在下列条件中:①∠A=∠C﹣∠B,②∠A:∠B:∠C=2:3:5,③∠A=90°﹣∠B,④∠B﹣∠C=90°中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
解:①因为∠A+∠B=∠C,则2∠C=180°,∠C=90°,所以△ABC是直角三角形;
②因为∠A:∠B:∠C=2:3:5,设∠A=2x,则2x+3x+5x=180,x=18°,∠C=18°×5=90°,所以△ABC是直角三角形;
③因为∠A=90°﹣∠B,所以∠A+∠B=90°,则∠C=180°﹣90°=90°,所以△ABC是直角三角形;
④因为∠B﹣∠C=90°,则∠B=90°+∠C,所以三角形为钝角三角形.
所以能确定△ABC是直角三角形的有①②③.
故选:C.
8.下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
解:A、两个图形不能完全重合,故本选项错误;
B、两个图形能够完全重合,故本选项正确;
C、两个图形不能完全重合,故本选项错误;
D、两个图形不能完全重合,故本选项错误;
故选:B.
9.下列说法正确的是( )
A.两个等边三角形一定是全等图形 B.两个全等图形面积一定相等
C.形状相同的两个图形一定全等 D.两个正方形一定是全等图形
解:A、两个等边三角形相似但不一定全等,故说法错误,不符合题意;
B、两个全等图形的面积一定相等,正确,符合题意;
C、形状相同的两个图形相似但不一定全等,故说法错误,不符合题意;
D、两个正方形相似但不一定全等,故说法错误,不符合题意,
故选:B.
10.如图,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是( )
A.∠A=∠D,∠B=∠E B.AC=DF,AB=DE
C.∠A=∠D,AB=DE D.AC=DF,CB=FE
解:A.添加条件∠A=∠D,∠B=∠E时,没有边的条件,故不能判定△ABC≌△DEF,
B.添加条件AC=DF,AB=DE,根据HL可证明△ABC≌△DEF,
C.添加条件∠A=∠D,AB=DE,根据AAS可证明△ABC≌△DEF,
D.添加条件AC=DF,CB=FE,根据SAS可证明△ABC≌△DEF,
故选:A.
11.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
A.SSS B.SAS C.ASA D.AAS
解:如图,连接AB、CD,
在△ABO和△DCO中,,
∴△ABO≌△DCO(SAS),
∴AB=CD.
故选:B.
12.如果将长度为a-2、a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是( )
A. a>-1 B. a>2 C. a>5 D. 无法确定
解:因为-2<2<5,
所以a-2<a+2<a+5,
所以由三角形三边关系可得a-2+a+2>a+5,
解得a>5.
则不等式的解集是a>5.
故选C.
二.填空题
13.如图,图中以BC为边的三角形的个数为 4 .
解:∵以BC为公共边的三角形有△BCD,△BCE,△BCF,△ABC,
∴以BC为公共边的三角形的个数是4个.
故答案为:4.
14.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上 3 根木条.
解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
故答案为:3.
15.已知△ABC的两条边长分别为2和5,则第三边c的取值范围是 3<c<7 .
解:由题意,得
5﹣2<c<5+2,
即3<c<7.
故答案为:3<c<7.
16.如图,图中由实线围成的图形与①是全等形的有 ②③ .(填序号)
解:由图可知,图上由实线围成的图形与①是全等形的有②,③,
故答案为:②③.
17.如图,已知AB=CD,只需再添一个条件就可以证明△ABC≌△CDA的是 AD .
A.BC=AD B.AD∥BC
C.∠B=∠D D.AB∥DC
解:A.根据BC=AD、AB=CD和AC=AC能推出△ABC≌△CDA(SSS);
B.∵AD∥BC,∴∠DAC=∠BCA,
∴根据AB=CD、AC=AC和∠BCA=∠DAC不能推出△ABC≌△CDA;
C.根据AB=CD,AC=AC和∠B=∠D不能推出△ABC≌△CDA;
D.∵AB∥DC,∴∠BAC=∠DCA,
根据AB=CD,∠BAC=∠DCA和AC=AC能推出△ABC≌△CDA(SAS);
故答案为:AD.
18.如图,在四边形ABCD中,AB=CB,AD=CD.若∠A=108°,则∠C的大小=________(度).
18.证明:连接BD,
∵在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),
∴∠C=∠A=108°,
故答案为:108
三.解答题
19.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上,三角形BDE与四边形ACDE的周长相等.
(1)求线段AE的长.
(2)若图中所有线段长度的和是53cm,求BC+DE的值.
解:(1)∵三角形BDE与四边形ACDE的周长相等,
∴BD+DE+BE=AC+AE+CD+DE,
∵BD=DC,
∴BE=AE+AC,
设AE=x cm,则BE=(10﹣x)cm,
由题意得,10﹣x=x+6.
解得,x=2,
∴AE=2cm;
(2)图中共有8条线段,
它们的和为:AE+EB+AB+AC+DE+BD+CD+BC=2AB+AC+2BC+DE,
由题意得,2AB+AC+2BC+DE=53,
∴2BC+DE=53﹣(2AB+AC)=53﹣(2×10+6)=27,
∴BC+DE=(cm).
20.如图,点E、C、D、A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.
求证:BC=EF.
证明:∵AB//DF,∴∠B=∠CPD,∠A=∠FDE,∵∠E=∠CPD,∴∠E=∠B,
在△ABC和△DEF中, , ∴△ABC △DEF(ASA), ∴BC=EF.
21.若a,b,c是△ABC三边的长,化简:|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a﹣b|.
解:∵a、b、c是△ABC的三边的长,
∴a+b﹣c>0,b﹣a﹣c<0,c﹣a﹣b<0,
∴原式=a+b﹣c﹣b+a+c+c﹣a﹣b=a﹣b+c.
22.人教版初中数学教科书八年级上册第84页探究了“三角形中边与角之间的不等关系”,部分原文如图.
(1)请证明文中的∠ADE>∠B
(2)如图2,在△ABC中,如果∠ACB>∠B,能否证明AB>AC?
小敏同学提供了一种方法:将△ABC折叠,使点B落在点C上,折痕交AB于点F,交BC于点G,再运用三角形三边关系即可证明,请你按照小敏的方法完成证明.
解:(1)∵∠ADE是△EBD的一个外角,∠B为与∠ADE不相邻的内角.
∴∠ADE>∠B.
(2)证明:∵将△ABC折叠,使点B落在点C上,
∴BF=CF,
在△ACF中,AF+FC>AC,即AF+BF>AC,
∴AB>AC.
23.如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE;
(2)解:∵△ABC≌△DEF,
∴AB=DE=6,
∵OE=4,
∴OD=DE﹣OE=6﹣4=2.
24.如图,已知在△ABC中,BD是∠ABC的角平分线,∠A=60°,∠BDC=80°,求∠DBC的度数.
解:∵∠A=60°,∠BDC=80°,
∴∠ABD=∠BDC﹣∠A=80°﹣60°=20°.
又∵BD是∠ABC的角平分线,
∴∠DBC=∠ABD=20°.
25.如图①,在△ABC中,D、E分别是AB,AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD,CE分别延长至M,N,使DM= BD,EN= CE,连接AM,AN,MN得到图③,请解答下列问题:
(1)在图②中,BD与CE的数量关系是________;
(2)在图③中,猜想AM与AN的数量关系,∠MAN与∠BAC的数量关系,并证明你的猜想.
解:(1)BD=CE
(2)解:AM=AN,∠MAN=∠BAC
∵ ∠DAE=∠BAC
∴ ∠CAE=∠BAD
在△BAD和△CAE中,
∴ △CAE≌△BAD(SAS)
∴ ∠ACE=∠ABD ,CE=BD
∵ DM= BD,EN= CE,BD=CE,
∴ BM=CN
在△ABM和△ACN中,
∴ △ABM≌△ACN(SAS)
∴ AM=AN, ∠BAM=∠CAN,∴∠MAN=∠BAC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
