2021-2022学年广东省广州市越秀区育才学校九年级(下)开学数学试卷(Word版含解析)
文档属性
| 名称 | 2021-2022学年广东省广州市越秀区育才学校九年级(下)开学数学试卷(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 16:38:33 | ||
图片预览


文档简介
2021-2022学年广东省广州市越秀区育才学校九年级(下)开学数学试卷
一、选择题(本大题共10题,每小题3分,满分30分)
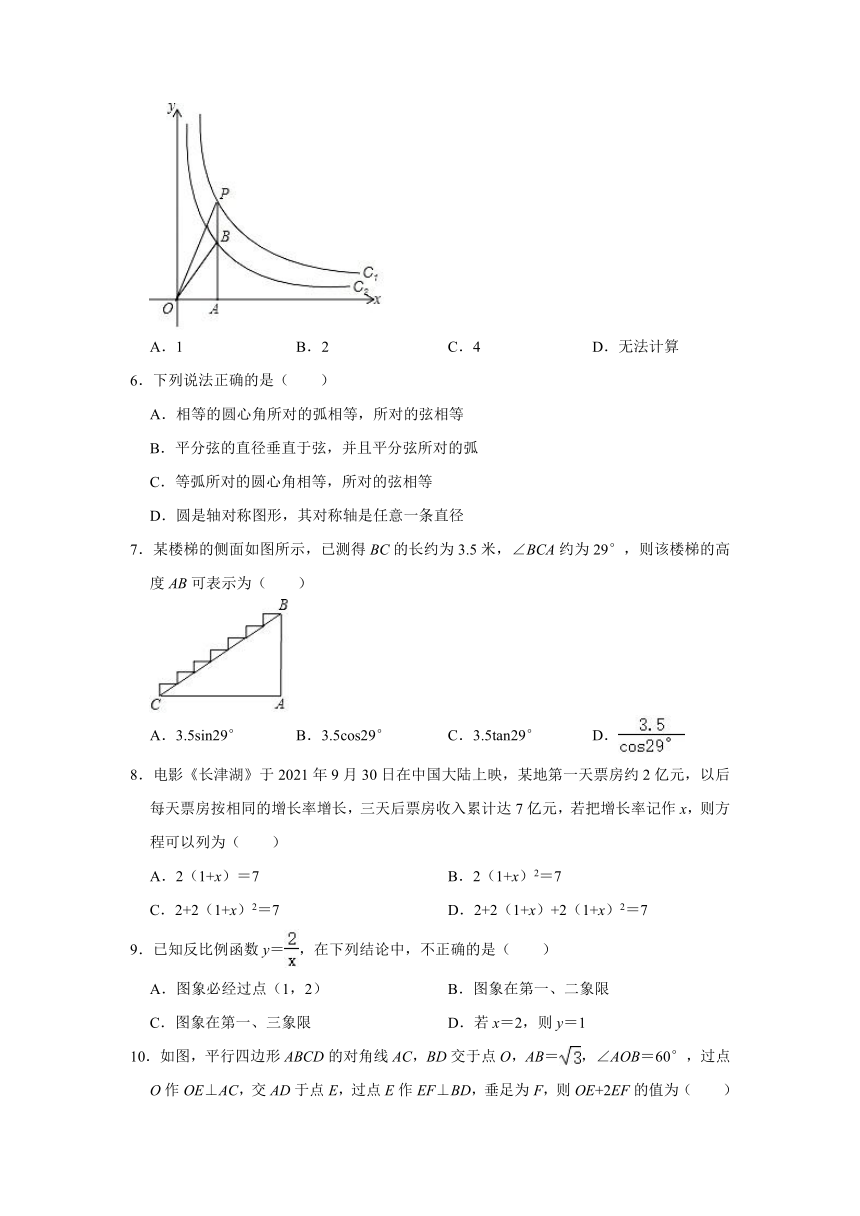
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.下列说法中正确的是( )
A.一组数据2、3、3、5、5、6,这组数据的众数是3
B.袋中有10个蓝球,1个绿球,随机摸出一个球是绿球的概率是0.1
C.为了解长沙市区全年水质情况,适合采用全面调查
D.画出一个三角形,其内角和是180°为必然事件
3.下列函数不是反比例函数的是( )
A.y=3x﹣1 B.xy=5 C.y=﹣ D.y=
4.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长
D.两人的影子长度不确定
5.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
A.1 B.2 C.4 D.无法计算
6.下列说法正确的是( )
A.相等的圆心角所对的弧相等,所对的弦相等
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.等弧所对的圆心角相等,所对的弦相等
D.圆是轴对称图形,其对称轴是任意一条直径
7.某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
A.3.5sin29° B.3.5cos29° C.3.5tan29° D.
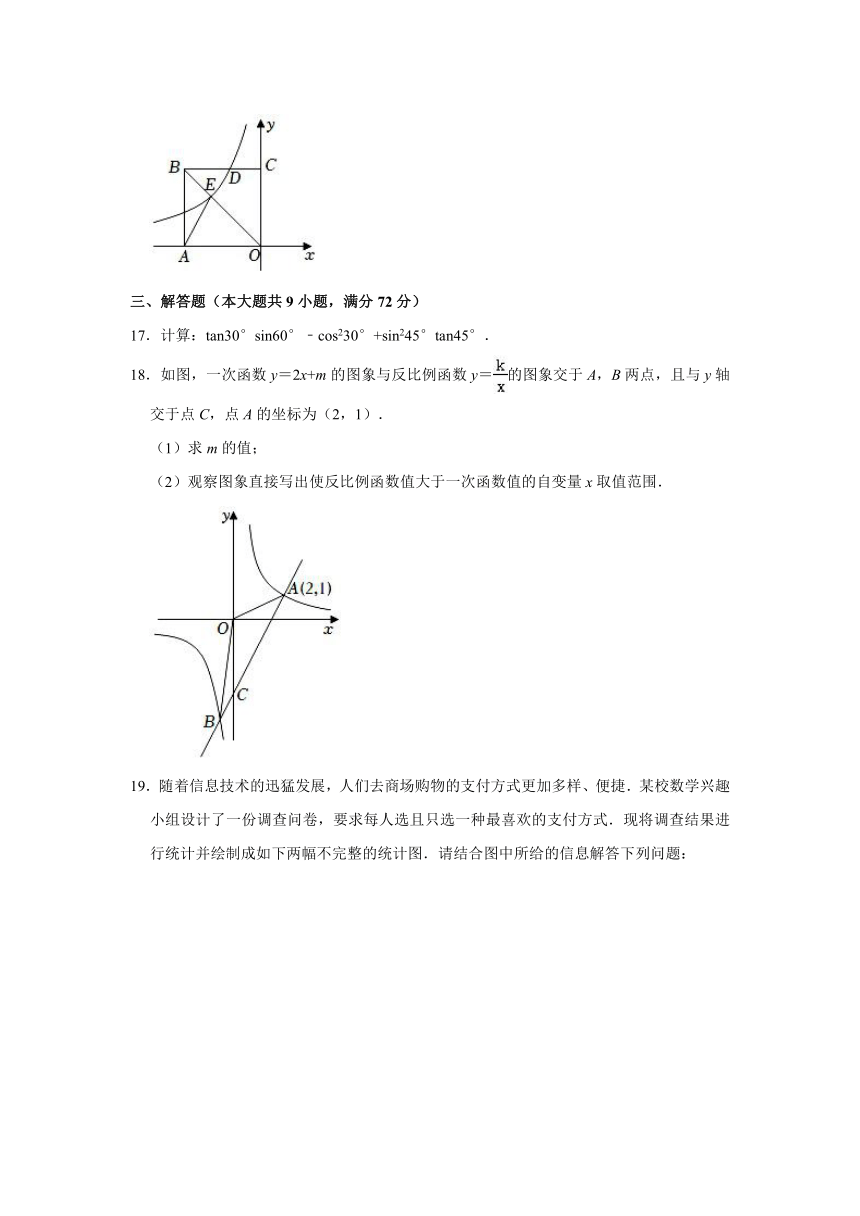
8.电影《长津湖》于2021年9月30日在中国大陆上映,某地第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后票房收入累计达7亿元,若把增长率记作x,则方程可以列为( )
A.2(1+x)=7 B.2(1+x)2=7
C.2+2(1+x)2=7 D.2+2(1+x)+2(1+x)2=7
9.已知反比例函数y=,在下列结论中,不正确的是( )
A.图象必经过点(1,2) B.图象在第一、二象限
C.图象在第一、三象限 D.若x=2,则y=1
10.如图,平行四边形ABCD的对角线AC,BD交于点O,AB=,∠AOB=60°,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+2EF的值为( )
A.+1 B. C. D.
二、填空题(本大题共6小,每小题3分,满分18分)
11.如图,是用若干个边长为1的小正方体堆积而成的几何体,该几何体的左视图的面积为 .
12.若点A(﹣3,y1),B(﹣1,y2),C(2,y3)都在反比例函数y=(k<0)的图象上,则y1,y2,y3的从小到大的关系是 .
13.一个圆锥的底面半径为5,高为12,则这个圆锥的全面积是 (结果保留π).
14.如图,如果小华沿坡度为的坡面由A到B行走了8米,那么他实际上升的高度为 米.
15.一副三角板如图放置,将三角板ABC绕点A顺时针旋转α(0°<α<90°)角度,使得三角板ABC的一边所在的直线与ED所在的直线垂直,则α的度数为 .
16.如图所示,反比例函数y=与矩形OABC的对角线OB交于点E,与BC交于点D,若BD:DC=5:4,且△AOE的面积为12,则k的值为 .
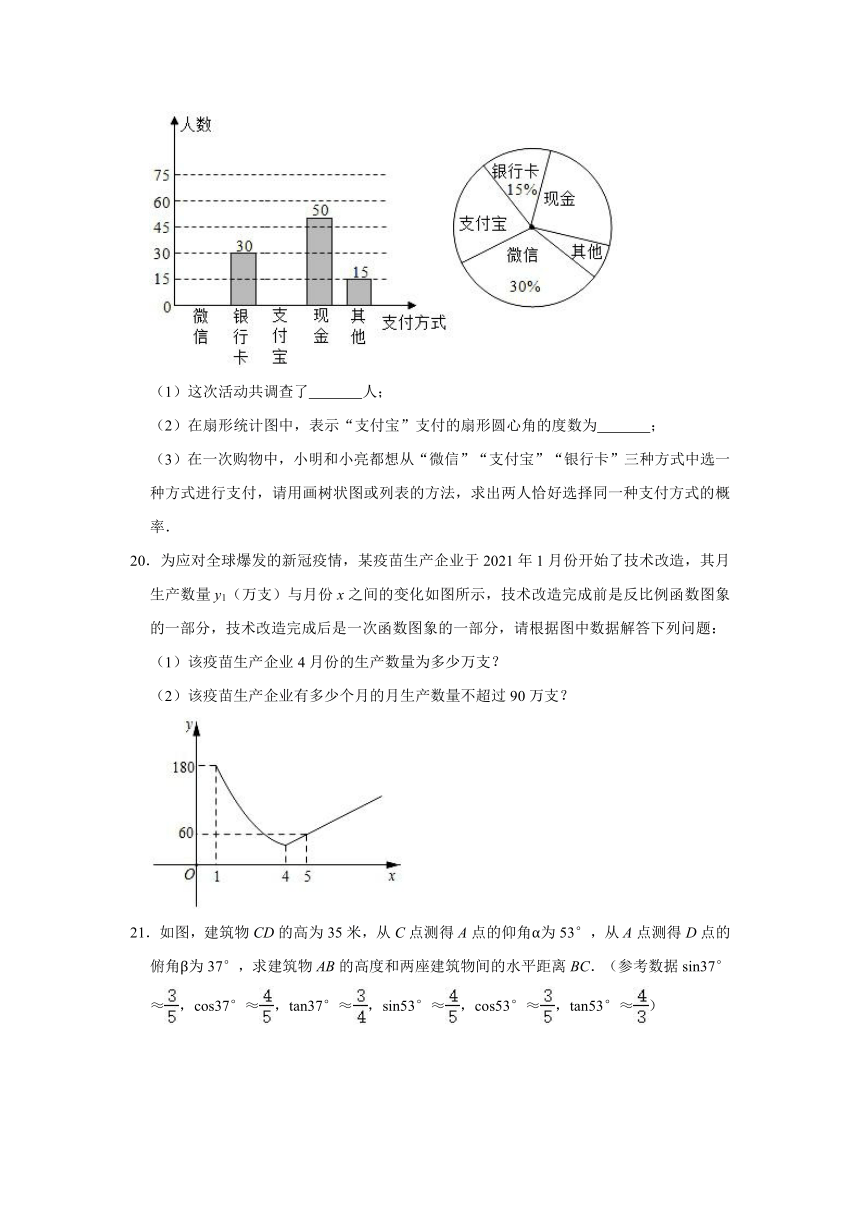
三、解答题(本大题共9小题,满分72分)
17.计算:tan30°sin60°﹣cos230°+sin245°tan45°.
18.如图,一次函数y=2x+m的图象与反比例函数y=的图象交于A,B两点,且与y轴交于点C,点A的坐标为(2,1).
(1)求m的值;
(2)观察图象直接写出使反比例函数值大于一次函数值的自变量x取值范围.
19.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
20.为应对全球爆发的新冠疫情,某疫苗生产企业于2021年1月份开始了技术改造,其月生产数量y1(万支)与月份x之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
(1)该疫苗生产企业4月份的生产数量为多少万支?
(2)该疫苗生产企业有多少个月的月生产数量不超过90万支?
21.如图,建筑物CD的高为35米,从C点测得A点的仰角α为53°,从A点测得D点的俯角β为37°,求建筑物AB的高度和两座建筑物间的水平距离BC.(参考数据sin37°≈,cos37°≈,tan37°≈,sin53°≈,cos53°≈,tan53°≈)
22.如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
(1)求证:DE为⊙O的切线;
(2)若AB=13,CD=5,求CE的长.
23.如图,抛物线y=﹣x2+bx+c的图象与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),直线l的函数表达式为y=﹣x+6.
(1)求抛物线的函数表达式;
(2)动点P在抛物线AB段上运动,经过点P作y轴的平行线交直线l于点Q,求线段PQ的取值范围.
24.已知抛物线y=x2+(3﹣m)x﹣2m+2.
(1)若抛物线经过坐标原点,求此时抛物线的解析式;
(2)该抛物线的顶点随着m的变化而移动,当顶点移到最高处时,求该抛物线的顶点坐标;
(3)已知点E(﹣1,1),F(3,5),若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.
25.在菱形ABCD中,AB=6,E为AB的中点,连接AC,DE交AC于点F,连接BF,记∠ABC=α(0°<α<180°).
(1)当α=60°时,求AF的长;
(2)若△BCF为等腰三角形,求AC的长;
(3)以BC为一边在菱形ABCD同侧作等边△GBC,连接GF,当α在变化的过程中,求GF的最小值.
参考答案
一、选择题(本大题共10题,每小题3分,满分30分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形、中心对称图形的定义即可判断.
解:A、不是中心对称图形,是轴对称图形,故本选项不符合题意;
B、既是轴对称图形又是中心对称图形,故本选项符合题意;
C、是中心对称图形,不是轴对称图形,故本选项不符合题意;
D、不是中心对称图形,是轴对称图形,故本选项不符合题意.
故选:B.
2.下列说法中正确的是( )
A.一组数据2、3、3、5、5、6,这组数据的众数是3
B.袋中有10个蓝球,1个绿球,随机摸出一个球是绿球的概率是0.1
C.为了解长沙市区全年水质情况,适合采用全面调查
D.画出一个三角形,其内角和是180°为必然事件
【分析】根据众数,概率公式,全面调查和抽样调查,事件发生的可能性大小判断即可.
解:A、一组数据2、3、3、5、5、6,这组数据的众数是3和5,本选项说法不符合题意;
B、袋中有10个蓝球,1个绿球,随机摸出一个球是绿球的概率是=,本选项说法不符合题意;
C、为了解长沙市区全年水质情况,适合采用抽样调查,本选项说法不符合题意;
D、画出一个三角形,其内角和是180°为必然事件,本选项说法符合题意.
故选:D.
3.下列函数不是反比例函数的是( )
A.y=3x﹣1 B.xy=5 C.y=﹣ D.y=
【分析】根据反比例函数的定义判断即可.
解:A.y=3x﹣1,是反比例函数,故A不符合题意;
B.xy=5,是反比例函数,故B不符合题意;
C.y=﹣,是正比例函数,故C符合题意;
D.y=,是反比例函数,故D不符合题意;
故选:C.
4.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长
D.两人的影子长度不确定
【分析】在同一路灯下由于位置不确定,根据中心投影的特点判断得出答案即可.
解:在同一路灯下由于位置不同,影长也不同,所以无法判断谁的影子长.
故选:D.
5.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
A.1 B.2 C.4 D.无法计算
【分析】根据反比例函数y=(k≠0)系数k的几何意义得到S△POA=×4=2,S△BOA=×2=1,然后利用S△POB=S△POA﹣S△BOA进行计算即可.
解:∵PA⊥x轴于点A,交C2于点B,
∴S△POA=×4=2,S△BOA=×2=1,
∴S△POB=2﹣1=1.
故选:A.
6.下列说法正确的是( )
A.相等的圆心角所对的弧相等,所对的弦相等
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.等弧所对的圆心角相等,所对的弦相等
D.圆是轴对称图形,其对称轴是任意一条直径
【分析】根据圆心角、弧、弦之间的关系即可判断选项A和选项C,根据圆的性质即可判断选项D,根据垂径定理即可判断选项B.
解:A.
如图1,圆心角∠AOB=圆心角∠COD,但是,弦AB≠弦CD,故本选项不符合题意;
B.
如图2,直径AB和弦CD,AB平分CD,但是AB和CD不垂直,故本选项不符合题意;
C.等弧所对的圆心角相等,所对的弦也相等,故本选项符合题意;
D.圆是轴对称图形,对称轴是直径所在的直线(对称轴是直线,不是线段),故本选项不符合题意;
故选:C.
7.某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
A.3.5sin29° B.3.5cos29° C.3.5tan29° D.
【分析】解直角三角形求出AB即可.
解:在Rt△ABC中,∵∠A=90°,BC=3.5米,∠BCA=29°,
∴AB=BC sin∠ACB=3.5 sin29°,
故选:A.
8.电影《长津湖》于2021年9月30日在中国大陆上映,某地第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后票房收入累计达7亿元,若把增长率记作x,则方程可以列为( )
A.2(1+x)=7 B.2(1+x)2=7
C.2+2(1+x)2=7 D.2+2(1+x)+2(1+x)2=7
【分析】若把增长率记作x,则第二天票房约为2(1+x)亿元,第三天票房约为2(1+x)2亿元,根据三天后票房收入累计达7亿元,即可得出关于x的一元二次方程,此题得解.
解:若把增长率记作x,则第二天票房约为2(1+x)亿元,第三天票房约为2(1+x)2亿元,
依题意得:2+2(1+x)+2(1+x)2=7.
故选:D.
9.已知反比例函数y=,在下列结论中,不正确的是( )
A.图象必经过点(1,2) B.图象在第一、二象限
C.图象在第一、三象限 D.若x=2,则y=1
【分析】由k=2>0即可判断B,C;把x=2,代入y=可判断A,D.
解:A.把(2,1)代入y=得:左边=右边,故本选项不符合题意;
B.k=2>0,图象在第一、三象限内,故本选项符合题意;
C.k=2>0,图象在第一、三象限内,故本选项不符合题意;
D.把x=2,代入y=得y=1,故本选项不符合题意;
故选:B.
10.如图,平行四边形ABCD的对角线AC,BD交于点O,AB=,∠AOB=60°,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+2EF的值为( )
A.+1 B. C. D.
【分析】依据含30°角的直角三角形的性质可求解AO=1,BO=2,利用三角形的面积公式计算△ABO的面积,结合平行四边形的性质可得DO=BO=2,S△ADO=S△ABO=,即可得到OE+2EF的值.
解:∵∠BAO=90°,∠AOB=60°,
∴∠ABO=30°,
∴BO=2AO,
∵AB=,
∴AO=1,BO=2,
∴S△ABO=AO AB=,
∵四边形ABCD为平行四边形,
∴DO=BO=2,S△ADO=S△ABO=,
∵OF⊥AO,EF⊥OD,
∴S△ADO=S△AEO+S△EDO===,
即OE+2EF=.
故选:B.
二、填空题(本大题共6小,每小题3分,满分18分)
11.如图,是用若干个边长为1的小正方体堆积而成的几何体,该几何体的左视图的面积为 3 .
【分析】先确定几何体的左视图,进而得出左视图的面积.
解:该几何体的左视图的底层是两个正方形,上层左边是一个正方形,
所以左视图是由三个正方形组成的图形,即该几何体的左视图的面积为3.
故答案为:3.
12.若点A(﹣3,y1),B(﹣1,y2),C(2,y3)都在反比例函数y=(k<0)的图象上,则y1,y2,y3的从小到大的关系是 y3<y1<y2 .
【分析】先根据反比例函数中k<0判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
解:∵反比例函数y=中k<0,
∴函数图象的两个分支分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵﹣3<0,﹣1<0,
∴点A(﹣3,y1),B(﹣1,y2)位于第二象限,
∴y1>0,y2>0,
∵﹣3<﹣1<0,
∴0<y1<y2.
∵2>0,
∴点C(2,y3)位于第四象限,
∴y3<0,
∴y3<y1<y2.
故答案为:y3<y1<y2.
13.一个圆锥的底面半径为5,高为12,则这个圆锥的全面积是 90π (结果保留π).
【分析】首先求得圆锥的底面周长,然后利用扇形的面积公式即可求解.
解:∵底面半径为5,高为12,
∴母线长为13,
底面圆的半径为5,则底面周长=10π,
侧面面积=×10π×13=65π;
底面积为25π,
全面积为:65π+25π=90π.
故答案为:90π.
14.如图,如果小华沿坡度为的坡面由A到B行走了8米,那么他实际上升的高度为 4 米.
【分析】根据斜坡AB的坡度求出坡角,根据含30°角的直角三角形的性质解答即可.
解:设斜坡AB的坡角为α,
∵斜坡AB的坡度为1:,
∴tanα==,
∴α=30°,
∴他实际上升的高度=AB=×8=4,
故答案为:4.
15.一副三角板如图放置,将三角板ABC绕点A顺时针旋转α(0°<α<90°)角度,使得三角板ABC的一边所在的直线与ED所在的直线垂直,则α的度数为 15°或45° .
【分析】分BC⊥DE,AC⊥DE两种情况讨论.
解:分情况讨论:
①当DE⊥BC时,∠BAD=180°﹣60°﹣45°=75°,
∴α=90°﹣∠BAD=15°;
②当AC⊥DE时,α=90°﹣∠E=90°﹣45°=45°.
故答案为:15°或45°.
16.如图所示,反比例函数y=与矩形OABC的对角线OB交于点E,与BC交于点D,若BD:DC=5:4,且△AOE的面积为12,则k的值为 ﹣16 .
【分析】由题意可知,设BD=5m,则DC=4m,所以BC=OA=9m,因为△AOE的面积为12,所以EF=;过点E作EF⊥x轴于点F,则EF∥AB,则EF:OF=AB:OA,代入可得出AB的长,进而表达点D的坐标,由反比例函数图象上点的坐标特征可列出方程求出k的值.
解:如图,过点E作EF⊥x轴于点F,
∵四边形ABCO是矩形,
∴∠BAO=90°,即AB⊥x轴,
∴EF∥AB,
∴EF:OF=BA:OA,
∵BD:DC=5:4,设BD=5m,
∴DC=4m,
∴BC=OA=9m,
∵△AOE的面积为12,
∴ OA EF=12,即=12,
解得EF=,
∵点E在反比例函数y=图象上,
∴E(,),
∴OF=﹣,
∴:(﹣)=BA:9m,
∴AB=﹣,
∴D(﹣4m,﹣),
∵点D在反比例函数y=图象上,
∴k=﹣4m (﹣),解得k=﹣16(正值舍去).
故答案为:﹣16.
三、解答题(本大题共9小题,满分72分)
17.计算:tan30°sin60°﹣cos230°+sin245°tan45°.
【分析】直接利用特殊角的三角函数值代入,进而利用二次根式的乘法运算法则计算得出答案.
解:原式=×﹣()2+()2×1
=﹣+
=.
18.如图,一次函数y=2x+m的图象与反比例函数y=的图象交于A,B两点,且与y轴交于点C,点A的坐标为(2,1).
(1)求m的值;
(2)观察图象直接写出使反比例函数值大于一次函数值的自变量x取值范围.
【分析】(1)把A点的坐标代入函数解析式,即可求出答案;
(2)解由两函数解析式组成的方程组,求出方程组的解,即可得出B点的坐标,然后根据函数的图象得出答案即可.
解:(1)∵一次函数y=2x+m的图象与反比例函数y=的图象交于A,B两点,点A的坐标为(2,1).
∴把A的坐标代入函数解析式得:1=4+m,k=2×1,
解得:m=﹣3,k=2,
故m的值为﹣3;
(2)解方程组得:或,
∴反比例函数值大于一次函数值的自变量x取值范围是x<﹣或0<x<2.
19.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 200 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 81° ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
【分析】(1)用支付宝、现金及其他的人数和除以这三者的百分比之和可得总人数;
(2)用360°乘以“支付宝”人数所占比例即可得;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两人恰好选择同一种支付方式的情况,再利用概率公式即可求得答案.
解:(1)这次活动共调查的人数为30÷15%=200(人),
故答案为:200;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为360°×=81°,
故答案为:81°;
(3)将微信记为A,支付宝记为B,银行卡记为C,列表格如下:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
共有9种等可能性的结果,其中两人恰好选择同一种支付方式的结果有3种,
则P(两人恰好选择同一种支付方式)=.
20.为应对全球爆发的新冠疫情,某疫苗生产企业于2021年1月份开始了技术改造,其月生产数量y1(万支)与月份x之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
(1)该疫苗生产企业4月份的生产数量为多少万支?
(2)该疫苗生产企业有多少个月的月生产数量不超过90万支?
【分析】(1)根据题意和图象中的数据,可以计算出技术改造完成前对应的函数解析式,然后将x=4代入求出相应的y的值即可;
(2)根据题意和图象中的数据,可以技术改造完成后y与x的函数解析式,然后即可列出相应的不等式组,求解即可,注意x为正整数.
解:(1)当1≤x≤4时,设y与x的函数关系式为y=,
∵点(1,180)在该函数图象上,
∴180=,得k=180,
∴y=,
当x=4时,y==45,
即该疫苗生产企业4月份的生产数量为45万支;
(2)设技术改造完成后对应的函数解析式为y=ax+b,
∵点(4,45),(5,60)在该函数图象上,
∴,
解得,
∴技术改造完成后对应的函数解析式为y=15x﹣15,
,
解得2≤x≤7
∵x为正整数,
∴x=2,3,4,5,6,7,
答:该疫苗生产企业有6个月的月生产数量不超过90万支.
21.如图,建筑物CD的高为35米,从C点测得A点的仰角α为53°,从A点测得D点的俯角β为37°,求建筑物AB的高度和两座建筑物间的水平距离BC.(参考数据sin37°≈,cos37°≈,tan37°≈,sin53°≈,cos53°≈,tan53°≈)
【分析】过点D作DE⊥AB,垂足为E.利用直角三角形的边角间关系,先在Rt△AED中用ED表示出AE,再在Rt△ABC中用BC表示出AB,根据线段的和差和矩形的性质可得到关于BC的方程,求解即可.
解:过点D作DE⊥AB,垂足为E.
由题意可知,四边形BEDC是矩形,
∴BE=CD=35米,,ED=BC.
∵AF∥ED,
∴∠ADE=∠FAD=β.
在Rt△AED中,
∵tan∠ADE=,
∴AE=tanβ DE=tan37° DE≈BC.
在Rt△ABC中,
∵tan∠ACB=,
∴AB=tanα BC=tan53° BC≈BC.
∵AB﹣AE=BE,
∴BC﹣BC=35.
∴BC=60.
∴AB=BC=80.
答:建筑物AB的高度为80米,两座建筑物间的水平距离BC为60米.
22.如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
(1)求证:DE为⊙O的切线;
(2)若AB=13,CD=5,求CE的长.
【分析】(1)如图,作辅助线;证明OD∥AC;由DE⊥AC,得到DE⊥AC,即可解决问题.
(2)如图,作辅助线;证明AC=AB=13;证明△CDE∽△CAD,得到,求出CE的长即可解决问题.
解:(1)连接OD;
∵D为BC的中点,O为AB的中点,
∴OD∥AC;
∵DE⊥AC,
∴DE⊥OD,
∴DE是圆O的切线.
(2)连接 AD;
∵AB是直径,
∴AD⊥BC;
∵D为BC的中点,
∴AD是BC的垂直平分线,
∴AC=AB=13;
∵∠C=∠C,∠DEC=∠ADC=90°,
∴△CDE∽△CAD,
∴,而AC=AB=13,CD=5,
∴CE=.
23.如图,抛物线y=﹣x2+bx+c的图象与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),直线l的函数表达式为y=﹣x+6.
(1)求抛物线的函数表达式;
(2)动点P在抛物线AB段上运动,经过点P作y轴的平行线交直线l于点Q,求线段PQ的取值范围.
【分析】(1)用待定系数法求函数解析式即可;
(2)根据已知和图形设出P、Q的坐标,再求出PQ=(m﹣)2+,由函数的性质和m的取值范围求出PQ的最大值和最小值即可.
解:(1)把A(3,0)和B(0,3)代入抛物线y=﹣x2+bx+c得:
,
解得:,
∴抛物线的函数表达式为y=y=﹣x2+2x+3;
(2)根据题意,设P(m,﹣m2+2m+3)(0≤m≤3),则Q(m,﹣m+6),
PQ=﹣m+6﹣(﹣m2+2m+3)=m2﹣3m+3=(m﹣)2+,
∵1>0,0≤m≤3,
∴当m=时,PQ最小,最小值为,
当m=0或3时,PQ最大,最大值为3,
∴线段PQ的取值范围≤PQ≤3.
24.已知抛物线y=x2+(3﹣m)x﹣2m+2.
(1)若抛物线经过坐标原点,求此时抛物线的解析式;
(2)该抛物线的顶点随着m的变化而移动,当顶点移到最高处时,求该抛物线的顶点坐标;
(3)已知点E(﹣1,1),F(3,5),若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.
【分析】(1)将(0,0)代入y=x2+(3﹣m)x﹣2m+2,用待定系数法可得抛物线的解析式为y=x2+2x;
(2)设抛物线y=x2+(3﹣m)x﹣2m+2的顶点坐标为(p,q),顶点移到最高处,即是q取最大值,而q==﹣(m+1)2,由二次函数性质即知m=﹣1时,q最大值是0,即可求得抛物线的顶点坐标为(﹣2,0);
(3)设直线EF为y=kx+b,由待定系数法可得直线EF为y=x+2,从而可求出直线y=x+2与抛物线y=x2+(3﹣m)x﹣2m+2的交点为(﹣2,0)和(m,m+2),由(﹣2,0)不在线段EF上,知(m,m+2)在线段EF上,即得﹣1≤m≤3,从而可得答案.
解:(1)将(0,0)代入y=x2+(3﹣m)x﹣2m+2得:
﹣2m+2=0,
解得m=1,
∴抛物线的解析式为y=x2+2x;
(2)设抛物线y=x2+(3﹣m)x﹣2m+2的顶点坐标为(p,q),
则p=,q=,
顶点移到最高处,即是q取最大值,
而q=
=
=
=﹣(m+1)2,
∵﹣<0,
∴m=﹣1时,q最大值是0,
此时p==﹣2,
∴当顶点移到最高处时,抛物线的顶点坐标为(﹣2,0);
(3)设直线EF为y=kx+b,
将E(﹣1,1),F(3,5)代入得:
,
解得,
∴直线EF为y=x+2,
由得或,
∴直线y=x+2与抛物线y=x2+(3﹣m)x﹣2m+2的交点为(﹣2,0)和(m,m+2),
而(﹣2,0)不在线段EF上,
∴若抛物线与线段EF只有一个交点,则(m,m+2)在线段EF上,
∴﹣1≤m≤3,
∴﹣2≤≤0,
∴抛物线顶点横坐标是范围是﹣2≤x顶点≤0.
25.在菱形ABCD中,AB=6,E为AB的中点,连接AC,DE交AC于点F,连接BF,记∠ABC=α(0°<α<180°).
(1)当α=60°时,求AF的长;
(2)若△BCF为等腰三角形,求AC的长;
(3)以BC为一边在菱形ABCD同侧作等边△GBC,连接GF,当α在变化的过程中,求GF的最小值.
【分析】(1)证明△ABC是等边三角形,利用平行线分线段成比例定理求解即可;
(2)分两种情形:如图2﹣1中,当CF=CB=6时,利用平行线分线段成比例定理求解.如图2﹣2中,当FB=FC时,利用相似三角形的性质求解;
(3)如图3中,过点G作GH⊥BC于点H,在BC上取一点O,使得OB=BC=2,连接OF,OG.想办法求出OF,OG,可得结论.
解:(1)如图1中,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=6,∠ABC=∠ADC=60°,AB∥CD,
∴△ABC是等边三角形,
∴AC=AB=6,
∵AE=EB,AE∥CD,
∴==,
∴AF=AC=2;
(2)如图2﹣1中,当CF=CB=6时,
∵AE∥CD,
∴==,
∴AF=3,
∴AC=AF+FC=3+6=9.
如图2﹣2中,当FB=FC时,
∵∠FBC=∠FCB=∠BAC,∠BCF=∠ACB,
∴△BCF∽△ACB,
∴=,
设AF=x,CF=2x,
∴=,
∴x=或﹣,
经检验x=是分式方程的解,
AC=3x=3.
综上所述,满足条件的AC的值为9或3.
(3)如图3中,过点G作GH⊥BC于点H,在BC上取一点O,使得OB=BC=2,连接OF,OG.
∵△BCG是等边三角形,GH⊥BC,
∴BH=CH=3,
∴GH=BH=3,OH=HB﹣OB=3﹣2=1,
∴OG===2,
∵AF=AC,OB=CB,
∴=,
∴OF∥AB,
∴==,
∴OF=4,
∵FG≥OG﹣OF=2﹣4,
∴FG的最小值为2﹣4.
一、选择题(本大题共10题,每小题3分,满分30分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.下列说法中正确的是( )
A.一组数据2、3、3、5、5、6,这组数据的众数是3
B.袋中有10个蓝球,1个绿球,随机摸出一个球是绿球的概率是0.1
C.为了解长沙市区全年水质情况,适合采用全面调查
D.画出一个三角形,其内角和是180°为必然事件
3.下列函数不是反比例函数的是( )
A.y=3x﹣1 B.xy=5 C.y=﹣ D.y=
4.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长
D.两人的影子长度不确定
5.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
A.1 B.2 C.4 D.无法计算
6.下列说法正确的是( )
A.相等的圆心角所对的弧相等,所对的弦相等
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.等弧所对的圆心角相等,所对的弦相等
D.圆是轴对称图形,其对称轴是任意一条直径
7.某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
A.3.5sin29° B.3.5cos29° C.3.5tan29° D.
8.电影《长津湖》于2021年9月30日在中国大陆上映,某地第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后票房收入累计达7亿元,若把增长率记作x,则方程可以列为( )
A.2(1+x)=7 B.2(1+x)2=7
C.2+2(1+x)2=7 D.2+2(1+x)+2(1+x)2=7
9.已知反比例函数y=,在下列结论中,不正确的是( )
A.图象必经过点(1,2) B.图象在第一、二象限
C.图象在第一、三象限 D.若x=2,则y=1
10.如图,平行四边形ABCD的对角线AC,BD交于点O,AB=,∠AOB=60°,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+2EF的值为( )
A.+1 B. C. D.
二、填空题(本大题共6小,每小题3分,满分18分)
11.如图,是用若干个边长为1的小正方体堆积而成的几何体,该几何体的左视图的面积为 .
12.若点A(﹣3,y1),B(﹣1,y2),C(2,y3)都在反比例函数y=(k<0)的图象上,则y1,y2,y3的从小到大的关系是 .
13.一个圆锥的底面半径为5,高为12,则这个圆锥的全面积是 (结果保留π).
14.如图,如果小华沿坡度为的坡面由A到B行走了8米,那么他实际上升的高度为 米.
15.一副三角板如图放置,将三角板ABC绕点A顺时针旋转α(0°<α<90°)角度,使得三角板ABC的一边所在的直线与ED所在的直线垂直,则α的度数为 .
16.如图所示,反比例函数y=与矩形OABC的对角线OB交于点E,与BC交于点D,若BD:DC=5:4,且△AOE的面积为12,则k的值为 .
三、解答题(本大题共9小题,满分72分)
17.计算:tan30°sin60°﹣cos230°+sin245°tan45°.
18.如图,一次函数y=2x+m的图象与反比例函数y=的图象交于A,B两点,且与y轴交于点C,点A的坐标为(2,1).
(1)求m的值;
(2)观察图象直接写出使反比例函数值大于一次函数值的自变量x取值范围.
19.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
20.为应对全球爆发的新冠疫情,某疫苗生产企业于2021年1月份开始了技术改造,其月生产数量y1(万支)与月份x之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
(1)该疫苗生产企业4月份的生产数量为多少万支?
(2)该疫苗生产企业有多少个月的月生产数量不超过90万支?
21.如图,建筑物CD的高为35米,从C点测得A点的仰角α为53°,从A点测得D点的俯角β为37°,求建筑物AB的高度和两座建筑物间的水平距离BC.(参考数据sin37°≈,cos37°≈,tan37°≈,sin53°≈,cos53°≈,tan53°≈)
22.如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
(1)求证:DE为⊙O的切线;
(2)若AB=13,CD=5,求CE的长.
23.如图,抛物线y=﹣x2+bx+c的图象与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),直线l的函数表达式为y=﹣x+6.
(1)求抛物线的函数表达式;
(2)动点P在抛物线AB段上运动,经过点P作y轴的平行线交直线l于点Q,求线段PQ的取值范围.
24.已知抛物线y=x2+(3﹣m)x﹣2m+2.
(1)若抛物线经过坐标原点,求此时抛物线的解析式;
(2)该抛物线的顶点随着m的变化而移动,当顶点移到最高处时,求该抛物线的顶点坐标;
(3)已知点E(﹣1,1),F(3,5),若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.
25.在菱形ABCD中,AB=6,E为AB的中点,连接AC,DE交AC于点F,连接BF,记∠ABC=α(0°<α<180°).
(1)当α=60°时,求AF的长;
(2)若△BCF为等腰三角形,求AC的长;
(3)以BC为一边在菱形ABCD同侧作等边△GBC,连接GF,当α在变化的过程中,求GF的最小值.
参考答案
一、选择题(本大题共10题,每小题3分,满分30分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形、中心对称图形的定义即可判断.
解:A、不是中心对称图形,是轴对称图形,故本选项不符合题意;
B、既是轴对称图形又是中心对称图形,故本选项符合题意;
C、是中心对称图形,不是轴对称图形,故本选项不符合题意;
D、不是中心对称图形,是轴对称图形,故本选项不符合题意.
故选:B.
2.下列说法中正确的是( )
A.一组数据2、3、3、5、5、6,这组数据的众数是3
B.袋中有10个蓝球,1个绿球,随机摸出一个球是绿球的概率是0.1
C.为了解长沙市区全年水质情况,适合采用全面调查
D.画出一个三角形,其内角和是180°为必然事件
【分析】根据众数,概率公式,全面调查和抽样调查,事件发生的可能性大小判断即可.
解:A、一组数据2、3、3、5、5、6,这组数据的众数是3和5,本选项说法不符合题意;
B、袋中有10个蓝球,1个绿球,随机摸出一个球是绿球的概率是=,本选项说法不符合题意;
C、为了解长沙市区全年水质情况,适合采用抽样调查,本选项说法不符合题意;
D、画出一个三角形,其内角和是180°为必然事件,本选项说法符合题意.
故选:D.
3.下列函数不是反比例函数的是( )
A.y=3x﹣1 B.xy=5 C.y=﹣ D.y=
【分析】根据反比例函数的定义判断即可.
解:A.y=3x﹣1,是反比例函数,故A不符合题意;
B.xy=5,是反比例函数,故B不符合题意;
C.y=﹣,是正比例函数,故C符合题意;
D.y=,是反比例函数,故D不符合题意;
故选:C.
4.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长
D.两人的影子长度不确定
【分析】在同一路灯下由于位置不确定,根据中心投影的特点判断得出答案即可.
解:在同一路灯下由于位置不同,影长也不同,所以无法判断谁的影子长.
故选:D.
5.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
A.1 B.2 C.4 D.无法计算
【分析】根据反比例函数y=(k≠0)系数k的几何意义得到S△POA=×4=2,S△BOA=×2=1,然后利用S△POB=S△POA﹣S△BOA进行计算即可.
解:∵PA⊥x轴于点A,交C2于点B,
∴S△POA=×4=2,S△BOA=×2=1,
∴S△POB=2﹣1=1.
故选:A.
6.下列说法正确的是( )
A.相等的圆心角所对的弧相等,所对的弦相等
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.等弧所对的圆心角相等,所对的弦相等
D.圆是轴对称图形,其对称轴是任意一条直径
【分析】根据圆心角、弧、弦之间的关系即可判断选项A和选项C,根据圆的性质即可判断选项D,根据垂径定理即可判断选项B.
解:A.
如图1,圆心角∠AOB=圆心角∠COD,但是,弦AB≠弦CD,故本选项不符合题意;
B.
如图2,直径AB和弦CD,AB平分CD,但是AB和CD不垂直,故本选项不符合题意;
C.等弧所对的圆心角相等,所对的弦也相等,故本选项符合题意;
D.圆是轴对称图形,对称轴是直径所在的直线(对称轴是直线,不是线段),故本选项不符合题意;
故选:C.
7.某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
A.3.5sin29° B.3.5cos29° C.3.5tan29° D.
【分析】解直角三角形求出AB即可.
解:在Rt△ABC中,∵∠A=90°,BC=3.5米,∠BCA=29°,
∴AB=BC sin∠ACB=3.5 sin29°,
故选:A.
8.电影《长津湖》于2021年9月30日在中国大陆上映,某地第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后票房收入累计达7亿元,若把增长率记作x,则方程可以列为( )
A.2(1+x)=7 B.2(1+x)2=7
C.2+2(1+x)2=7 D.2+2(1+x)+2(1+x)2=7
【分析】若把增长率记作x,则第二天票房约为2(1+x)亿元,第三天票房约为2(1+x)2亿元,根据三天后票房收入累计达7亿元,即可得出关于x的一元二次方程,此题得解.
解:若把增长率记作x,则第二天票房约为2(1+x)亿元,第三天票房约为2(1+x)2亿元,
依题意得:2+2(1+x)+2(1+x)2=7.
故选:D.
9.已知反比例函数y=,在下列结论中,不正确的是( )
A.图象必经过点(1,2) B.图象在第一、二象限
C.图象在第一、三象限 D.若x=2,则y=1
【分析】由k=2>0即可判断B,C;把x=2,代入y=可判断A,D.
解:A.把(2,1)代入y=得:左边=右边,故本选项不符合题意;
B.k=2>0,图象在第一、三象限内,故本选项符合题意;
C.k=2>0,图象在第一、三象限内,故本选项不符合题意;
D.把x=2,代入y=得y=1,故本选项不符合题意;
故选:B.
10.如图,平行四边形ABCD的对角线AC,BD交于点O,AB=,∠AOB=60°,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+2EF的值为( )
A.+1 B. C. D.
【分析】依据含30°角的直角三角形的性质可求解AO=1,BO=2,利用三角形的面积公式计算△ABO的面积,结合平行四边形的性质可得DO=BO=2,S△ADO=S△ABO=,即可得到OE+2EF的值.
解:∵∠BAO=90°,∠AOB=60°,
∴∠ABO=30°,
∴BO=2AO,
∵AB=,
∴AO=1,BO=2,
∴S△ABO=AO AB=,
∵四边形ABCD为平行四边形,
∴DO=BO=2,S△ADO=S△ABO=,
∵OF⊥AO,EF⊥OD,
∴S△ADO=S△AEO+S△EDO===,
即OE+2EF=.
故选:B.
二、填空题(本大题共6小,每小题3分,满分18分)
11.如图,是用若干个边长为1的小正方体堆积而成的几何体,该几何体的左视图的面积为 3 .
【分析】先确定几何体的左视图,进而得出左视图的面积.
解:该几何体的左视图的底层是两个正方形,上层左边是一个正方形,
所以左视图是由三个正方形组成的图形,即该几何体的左视图的面积为3.
故答案为:3.
12.若点A(﹣3,y1),B(﹣1,y2),C(2,y3)都在反比例函数y=(k<0)的图象上,则y1,y2,y3的从小到大的关系是 y3<y1<y2 .
【分析】先根据反比例函数中k<0判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
解:∵反比例函数y=中k<0,
∴函数图象的两个分支分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵﹣3<0,﹣1<0,
∴点A(﹣3,y1),B(﹣1,y2)位于第二象限,
∴y1>0,y2>0,
∵﹣3<﹣1<0,
∴0<y1<y2.
∵2>0,
∴点C(2,y3)位于第四象限,
∴y3<0,
∴y3<y1<y2.
故答案为:y3<y1<y2.
13.一个圆锥的底面半径为5,高为12,则这个圆锥的全面积是 90π (结果保留π).
【分析】首先求得圆锥的底面周长,然后利用扇形的面积公式即可求解.
解:∵底面半径为5,高为12,
∴母线长为13,
底面圆的半径为5,则底面周长=10π,
侧面面积=×10π×13=65π;
底面积为25π,
全面积为:65π+25π=90π.
故答案为:90π.
14.如图,如果小华沿坡度为的坡面由A到B行走了8米,那么他实际上升的高度为 4 米.
【分析】根据斜坡AB的坡度求出坡角,根据含30°角的直角三角形的性质解答即可.
解:设斜坡AB的坡角为α,
∵斜坡AB的坡度为1:,
∴tanα==,
∴α=30°,
∴他实际上升的高度=AB=×8=4,
故答案为:4.
15.一副三角板如图放置,将三角板ABC绕点A顺时针旋转α(0°<α<90°)角度,使得三角板ABC的一边所在的直线与ED所在的直线垂直,则α的度数为 15°或45° .
【分析】分BC⊥DE,AC⊥DE两种情况讨论.
解:分情况讨论:
①当DE⊥BC时,∠BAD=180°﹣60°﹣45°=75°,
∴α=90°﹣∠BAD=15°;
②当AC⊥DE时,α=90°﹣∠E=90°﹣45°=45°.
故答案为:15°或45°.
16.如图所示,反比例函数y=与矩形OABC的对角线OB交于点E,与BC交于点D,若BD:DC=5:4,且△AOE的面积为12,则k的值为 ﹣16 .
【分析】由题意可知,设BD=5m,则DC=4m,所以BC=OA=9m,因为△AOE的面积为12,所以EF=;过点E作EF⊥x轴于点F,则EF∥AB,则EF:OF=AB:OA,代入可得出AB的长,进而表达点D的坐标,由反比例函数图象上点的坐标特征可列出方程求出k的值.
解:如图,过点E作EF⊥x轴于点F,
∵四边形ABCO是矩形,
∴∠BAO=90°,即AB⊥x轴,
∴EF∥AB,
∴EF:OF=BA:OA,
∵BD:DC=5:4,设BD=5m,
∴DC=4m,
∴BC=OA=9m,
∵△AOE的面积为12,
∴ OA EF=12,即=12,
解得EF=,
∵点E在反比例函数y=图象上,
∴E(,),
∴OF=﹣,
∴:(﹣)=BA:9m,
∴AB=﹣,
∴D(﹣4m,﹣),
∵点D在反比例函数y=图象上,
∴k=﹣4m (﹣),解得k=﹣16(正值舍去).
故答案为:﹣16.
三、解答题(本大题共9小题,满分72分)
17.计算:tan30°sin60°﹣cos230°+sin245°tan45°.
【分析】直接利用特殊角的三角函数值代入,进而利用二次根式的乘法运算法则计算得出答案.
解:原式=×﹣()2+()2×1
=﹣+
=.
18.如图,一次函数y=2x+m的图象与反比例函数y=的图象交于A,B两点,且与y轴交于点C,点A的坐标为(2,1).
(1)求m的值;
(2)观察图象直接写出使反比例函数值大于一次函数值的自变量x取值范围.
【分析】(1)把A点的坐标代入函数解析式,即可求出答案;
(2)解由两函数解析式组成的方程组,求出方程组的解,即可得出B点的坐标,然后根据函数的图象得出答案即可.
解:(1)∵一次函数y=2x+m的图象与反比例函数y=的图象交于A,B两点,点A的坐标为(2,1).
∴把A的坐标代入函数解析式得:1=4+m,k=2×1,
解得:m=﹣3,k=2,
故m的值为﹣3;
(2)解方程组得:或,
∴反比例函数值大于一次函数值的自变量x取值范围是x<﹣或0<x<2.
19.随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 200 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 81° ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
【分析】(1)用支付宝、现金及其他的人数和除以这三者的百分比之和可得总人数;
(2)用360°乘以“支付宝”人数所占比例即可得;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两人恰好选择同一种支付方式的情况,再利用概率公式即可求得答案.
解:(1)这次活动共调查的人数为30÷15%=200(人),
故答案为:200;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为360°×=81°,
故答案为:81°;
(3)将微信记为A,支付宝记为B,银行卡记为C,列表格如下:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
共有9种等可能性的结果,其中两人恰好选择同一种支付方式的结果有3种,
则P(两人恰好选择同一种支付方式)=.
20.为应对全球爆发的新冠疫情,某疫苗生产企业于2021年1月份开始了技术改造,其月生产数量y1(万支)与月份x之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
(1)该疫苗生产企业4月份的生产数量为多少万支?
(2)该疫苗生产企业有多少个月的月生产数量不超过90万支?
【分析】(1)根据题意和图象中的数据,可以计算出技术改造完成前对应的函数解析式,然后将x=4代入求出相应的y的值即可;
(2)根据题意和图象中的数据,可以技术改造完成后y与x的函数解析式,然后即可列出相应的不等式组,求解即可,注意x为正整数.
解:(1)当1≤x≤4时,设y与x的函数关系式为y=,
∵点(1,180)在该函数图象上,
∴180=,得k=180,
∴y=,
当x=4时,y==45,
即该疫苗生产企业4月份的生产数量为45万支;
(2)设技术改造完成后对应的函数解析式为y=ax+b,
∵点(4,45),(5,60)在该函数图象上,
∴,
解得,
∴技术改造完成后对应的函数解析式为y=15x﹣15,
,
解得2≤x≤7
∵x为正整数,
∴x=2,3,4,5,6,7,
答:该疫苗生产企业有6个月的月生产数量不超过90万支.
21.如图,建筑物CD的高为35米,从C点测得A点的仰角α为53°,从A点测得D点的俯角β为37°,求建筑物AB的高度和两座建筑物间的水平距离BC.(参考数据sin37°≈,cos37°≈,tan37°≈,sin53°≈,cos53°≈,tan53°≈)
【分析】过点D作DE⊥AB,垂足为E.利用直角三角形的边角间关系,先在Rt△AED中用ED表示出AE,再在Rt△ABC中用BC表示出AB,根据线段的和差和矩形的性质可得到关于BC的方程,求解即可.
解:过点D作DE⊥AB,垂足为E.
由题意可知,四边形BEDC是矩形,
∴BE=CD=35米,,ED=BC.
∵AF∥ED,
∴∠ADE=∠FAD=β.
在Rt△AED中,
∵tan∠ADE=,
∴AE=tanβ DE=tan37° DE≈BC.
在Rt△ABC中,
∵tan∠ACB=,
∴AB=tanα BC=tan53° BC≈BC.
∵AB﹣AE=BE,
∴BC﹣BC=35.
∴BC=60.
∴AB=BC=80.
答:建筑物AB的高度为80米,两座建筑物间的水平距离BC为60米.
22.如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
(1)求证:DE为⊙O的切线;
(2)若AB=13,CD=5,求CE的长.
【分析】(1)如图,作辅助线;证明OD∥AC;由DE⊥AC,得到DE⊥AC,即可解决问题.
(2)如图,作辅助线;证明AC=AB=13;证明△CDE∽△CAD,得到,求出CE的长即可解决问题.
解:(1)连接OD;
∵D为BC的中点,O为AB的中点,
∴OD∥AC;
∵DE⊥AC,
∴DE⊥OD,
∴DE是圆O的切线.
(2)连接 AD;
∵AB是直径,
∴AD⊥BC;
∵D为BC的中点,
∴AD是BC的垂直平分线,
∴AC=AB=13;
∵∠C=∠C,∠DEC=∠ADC=90°,
∴△CDE∽△CAD,
∴,而AC=AB=13,CD=5,
∴CE=.
23.如图,抛物线y=﹣x2+bx+c的图象与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),直线l的函数表达式为y=﹣x+6.
(1)求抛物线的函数表达式;
(2)动点P在抛物线AB段上运动,经过点P作y轴的平行线交直线l于点Q,求线段PQ的取值范围.
【分析】(1)用待定系数法求函数解析式即可;
(2)根据已知和图形设出P、Q的坐标,再求出PQ=(m﹣)2+,由函数的性质和m的取值范围求出PQ的最大值和最小值即可.
解:(1)把A(3,0)和B(0,3)代入抛物线y=﹣x2+bx+c得:
,
解得:,
∴抛物线的函数表达式为y=y=﹣x2+2x+3;
(2)根据题意,设P(m,﹣m2+2m+3)(0≤m≤3),则Q(m,﹣m+6),
PQ=﹣m+6﹣(﹣m2+2m+3)=m2﹣3m+3=(m﹣)2+,
∵1>0,0≤m≤3,
∴当m=时,PQ最小,最小值为,
当m=0或3时,PQ最大,最大值为3,
∴线段PQ的取值范围≤PQ≤3.
24.已知抛物线y=x2+(3﹣m)x﹣2m+2.
(1)若抛物线经过坐标原点,求此时抛物线的解析式;
(2)该抛物线的顶点随着m的变化而移动,当顶点移到最高处时,求该抛物线的顶点坐标;
(3)已知点E(﹣1,1),F(3,5),若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.
【分析】(1)将(0,0)代入y=x2+(3﹣m)x﹣2m+2,用待定系数法可得抛物线的解析式为y=x2+2x;
(2)设抛物线y=x2+(3﹣m)x﹣2m+2的顶点坐标为(p,q),顶点移到最高处,即是q取最大值,而q==﹣(m+1)2,由二次函数性质即知m=﹣1时,q最大值是0,即可求得抛物线的顶点坐标为(﹣2,0);
(3)设直线EF为y=kx+b,由待定系数法可得直线EF为y=x+2,从而可求出直线y=x+2与抛物线y=x2+(3﹣m)x﹣2m+2的交点为(﹣2,0)和(m,m+2),由(﹣2,0)不在线段EF上,知(m,m+2)在线段EF上,即得﹣1≤m≤3,从而可得答案.
解:(1)将(0,0)代入y=x2+(3﹣m)x﹣2m+2得:
﹣2m+2=0,
解得m=1,
∴抛物线的解析式为y=x2+2x;
(2)设抛物线y=x2+(3﹣m)x﹣2m+2的顶点坐标为(p,q),
则p=,q=,
顶点移到最高处,即是q取最大值,
而q=
=
=
=﹣(m+1)2,
∵﹣<0,
∴m=﹣1时,q最大值是0,
此时p==﹣2,
∴当顶点移到最高处时,抛物线的顶点坐标为(﹣2,0);
(3)设直线EF为y=kx+b,
将E(﹣1,1),F(3,5)代入得:
,
解得,
∴直线EF为y=x+2,
由得或,
∴直线y=x+2与抛物线y=x2+(3﹣m)x﹣2m+2的交点为(﹣2,0)和(m,m+2),
而(﹣2,0)不在线段EF上,
∴若抛物线与线段EF只有一个交点,则(m,m+2)在线段EF上,
∴﹣1≤m≤3,
∴﹣2≤≤0,
∴抛物线顶点横坐标是范围是﹣2≤x顶点≤0.
25.在菱形ABCD中,AB=6,E为AB的中点,连接AC,DE交AC于点F,连接BF,记∠ABC=α(0°<α<180°).
(1)当α=60°时,求AF的长;
(2)若△BCF为等腰三角形,求AC的长;
(3)以BC为一边在菱形ABCD同侧作等边△GBC,连接GF,当α在变化的过程中,求GF的最小值.
【分析】(1)证明△ABC是等边三角形,利用平行线分线段成比例定理求解即可;
(2)分两种情形:如图2﹣1中,当CF=CB=6时,利用平行线分线段成比例定理求解.如图2﹣2中,当FB=FC时,利用相似三角形的性质求解;
(3)如图3中,过点G作GH⊥BC于点H,在BC上取一点O,使得OB=BC=2,连接OF,OG.想办法求出OF,OG,可得结论.
解:(1)如图1中,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=6,∠ABC=∠ADC=60°,AB∥CD,
∴△ABC是等边三角形,
∴AC=AB=6,
∵AE=EB,AE∥CD,
∴==,
∴AF=AC=2;
(2)如图2﹣1中,当CF=CB=6时,
∵AE∥CD,
∴==,
∴AF=3,
∴AC=AF+FC=3+6=9.
如图2﹣2中,当FB=FC时,
∵∠FBC=∠FCB=∠BAC,∠BCF=∠ACB,
∴△BCF∽△ACB,
∴=,
设AF=x,CF=2x,
∴=,
∴x=或﹣,
经检验x=是分式方程的解,
AC=3x=3.
综上所述,满足条件的AC的值为9或3.
(3)如图3中,过点G作GH⊥BC于点H,在BC上取一点O,使得OB=BC=2,连接OF,OG.
∵△BCG是等边三角形,GH⊥BC,
∴BH=CH=3,
∴GH=BH=3,OH=HB﹣OB=3﹣2=1,
∴OG===2,
∵AF=AC,OB=CB,
∴=,
∴OF∥AB,
∴==,
∴OF=4,
∵FG≥OG﹣OF=2﹣4,
∴FG的最小值为2﹣4.
同课章节目录
