3.2.2直线的两点式方程课件
文档属性
| 名称 | 3.2.2直线的两点式方程课件 |  | |
| 格式 | zip | ||
| 文件大小 | 364.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-25 08:25:48 | ||
图片预览







文档简介
课件26张PPT。3.2.2 直线的两点式方程 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作 y=kx+b y- y0 =k(x- x0 )复习
巩固1). 直线的点斜式方程:2). 直线的斜截式方程:k为斜率, P0(x0 ,y0)为经过直线的点 k为斜率,b为截距一、复习、引入思考1 已知直线l过A(3,-5)和B(-2,5),如何求直线l的方程.解:∵直线l过点A(3,-5)和B(-2,5) 化成比例式: 思考2 设直线l经过两点P1(x1,y1),P2(x2,y2),(其中x1≠x2,y1≠y2),你能写出直线l的点斜式方程吗?两点式适用于与两坐标轴不垂直的直线.二、 直线的两点式方程 经过直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2,
y1≠y2 )的直线方程叫做直线的两点式方程,简称两点式.不是! 是不是已知任一直线中的两点就 能用两点式 写出直线方程呢? 两点式不能表示平行于坐标轴或与坐标轴重合的直线.注意: 当x1 =x2或y1= y2时,直线P1 P2没有两点式方程.( 因为x1 =x2或y1= y2时,两点式的分母为零,没有意义)
那么两点式不能用来表示哪些直线的方程呢??三、两点式方程的适应范围 若点P1 ( x1 , y1 ),P2( x2 , y2)
中有x1 =x2 ,或y1= y2,此时过这两点的直线方程是什么?当x1 =x2 时
方程为: x =x1当 y1= y2时
方程为: y= y1练习一 写出过下列两点的直线的两点式方程:
1、M(2,1),N(0,-3)
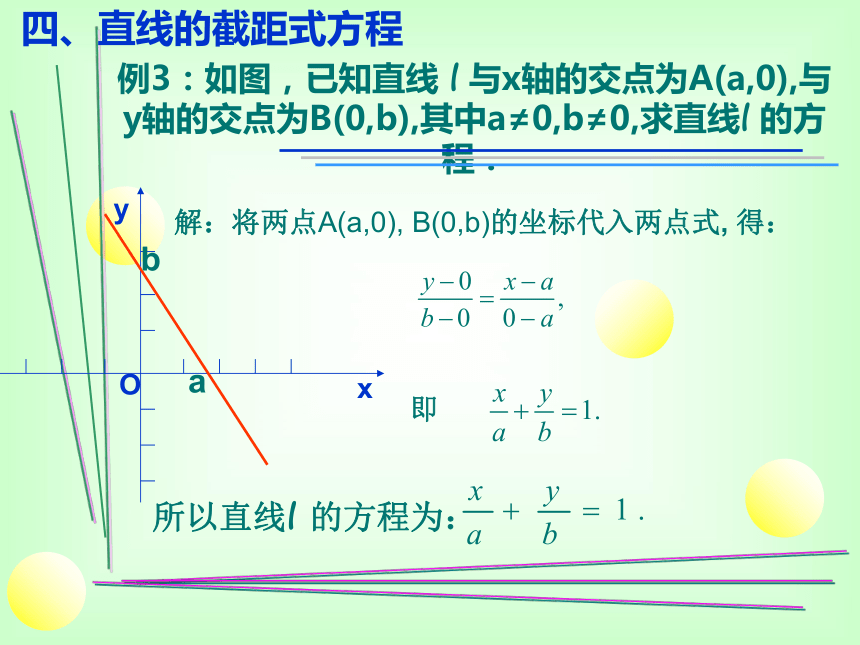
2、A(5,0),B(0,5) 例3:如图,已知直线 l 与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l 的方程. 解:将两点A(a,0), B(0,b)的坐标代入两点式, 得:即所以直线l 的方程为:四、直线的截距式方程ab②截距可是正数,负数和零 注意:①不能表示过原点或与坐标轴平行或重合的直线 直线与x轴的交点(o,a)的横坐标a叫做直线在x轴上的截距是不是任意一条直线都有其截距式方程呢?截距式直线方程: 直线与y轴的交点(b,0)的纵坐标b叫做直
线在y轴上的截距探究二:直线的截距式方程AB,C,D练习二 根据下列条件,求直线的截距式方程 1、在x轴上的截距是2,在y轴上的截距是3;
2、在x轴上的截距是-5,在y轴上的截距是6⑴ 过(1,2)并且在两个坐标轴上的截距相 等的直线有几条?解: ⑴ 两条例3:那还有一条呢?y=2x (与x轴和y轴的截距都为0)所以直线方程为:x+y-3=0a=3把(1,2)代入得:设 直线的方程为:解:三条 ⑵ 过(1,2)并且在两个坐标轴上的截距的绝对值相等的直线有几条? 解得:a=b=3或a=-b=-1直线方程为:y+x-3=0、y-x-1=0或y=2x设 例4:已知三角形的三个顶点是A(-5,0), B(3,-3),C(0,2),求BC边所在的直线 方程,以及该边上中线的直线方程。解:过B(3,-3),C(0,2)两点式方程为:整理得:5x+3y-6=0这就是BC边所在直线的方程。五、直线方程的应用 BC边上的中线是顶点A与BC边中点M所连线段,由中点坐标公式可得点M的坐标为:即整理得:x+13y+5=0
这就是BC边上中线所在的直线的方程。 过A(-5,0),M 的直线方程中点坐标公式:
则 若P1 ,P2坐标分别为( x1 ,y1 ), (x2 ,y2)
且中点M的坐标为(x,y).∵B(3,-3),C(0,2)
∴ M 不垂直x轴不垂直x轴不垂直两个坐标轴不垂直两个坐标
轴且不经过原点各类方程的适用范围灵活选取方程的形式来求方程补充例题: 根据下列条件,写出直线的方程(1)倾斜角为30°,经过A(8,-2);(2)经过点B(-2,0),且与x轴垂直;(3)斜率为-4,在y轴上的截距为7;(4)经过点A(-1,8),B(4,-2);(5)在y轴上的截距是2,且与x轴平行;(6)在x轴,y轴上的截距分别是4,-3;1、求过点P( 2, 1)的直线与两坐标轴正半轴所围成的三角形的面积最小时的直线方程补充练习 2、已知两点A(-3,4),B(3, 2),过点P(2,-1)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围
(2)求直线l的倾斜角α的取值范围补充练习思考题: 已知直线l 2x+y+3=0,求关于点A(1,2)对称的直线l 1的方程。 解:当x=0时,y=-3.
(0,-3)在直线l上,关于(1,2)的对称点为(2,7). 当x=-2时,y=1.
(-2,1)在直线l上,关于(1,2)的对称点为(4,3).
那么,点 (2,7) ,(4,3)在l 1上因此,直线l 1的方程为:化简得: 2x + y -11=0还有其它的方法吗?∵ l ∥l 1,所以l 与l 1的斜率相同,∴ kl1=-2经计算,l 1过点(4,3)所以直线的点斜式方程为:y-3=-2(x-4)化简得: 2x + y -11=03)中点坐标:课堂总结:1)直线的两点式方程2)两点式直线方程的适应范围4)直线的截距式方程:5)截距式直线方程的适应范围课后作业:
P97练习:1,2.(做书上)
P100习题3.2A组:3,4,8,9.
巩固1). 直线的点斜式方程:2). 直线的斜截式方程:k为斜率, P0(x0 ,y0)为经过直线的点 k为斜率,b为截距一、复习、引入思考1 已知直线l过A(3,-5)和B(-2,5),如何求直线l的方程.解:∵直线l过点A(3,-5)和B(-2,5) 化成比例式: 思考2 设直线l经过两点P1(x1,y1),P2(x2,y2),(其中x1≠x2,y1≠y2),你能写出直线l的点斜式方程吗?两点式适用于与两坐标轴不垂直的直线.二、 直线的两点式方程 经过直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2,
y1≠y2 )的直线方程叫做直线的两点式方程,简称两点式.不是! 是不是已知任一直线中的两点就 能用两点式 写出直线方程呢? 两点式不能表示平行于坐标轴或与坐标轴重合的直线.注意: 当x1 =x2或y1= y2时,直线P1 P2没有两点式方程.( 因为x1 =x2或y1= y2时,两点式的分母为零,没有意义)
那么两点式不能用来表示哪些直线的方程呢??三、两点式方程的适应范围 若点P1 ( x1 , y1 ),P2( x2 , y2)
中有x1 =x2 ,或y1= y2,此时过这两点的直线方程是什么?当x1 =x2 时
方程为: x =x1当 y1= y2时
方程为: y= y1练习一 写出过下列两点的直线的两点式方程:
1、M(2,1),N(0,-3)
2、A(5,0),B(0,5) 例3:如图,已知直线 l 与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l 的方程. 解:将两点A(a,0), B(0,b)的坐标代入两点式, 得:即所以直线l 的方程为:四、直线的截距式方程ab②截距可是正数,负数和零 注意:①不能表示过原点或与坐标轴平行或重合的直线 直线与x轴的交点(o,a)的横坐标a叫做直线在x轴上的截距是不是任意一条直线都有其截距式方程呢?截距式直线方程: 直线与y轴的交点(b,0)的纵坐标b叫做直
线在y轴上的截距探究二:直线的截距式方程AB,C,D练习二 根据下列条件,求直线的截距式方程 1、在x轴上的截距是2,在y轴上的截距是3;
2、在x轴上的截距是-5,在y轴上的截距是6⑴ 过(1,2)并且在两个坐标轴上的截距相 等的直线有几条?解: ⑴ 两条例3:那还有一条呢?y=2x (与x轴和y轴的截距都为0)所以直线方程为:x+y-3=0a=3把(1,2)代入得:设 直线的方程为:解:三条 ⑵ 过(1,2)并且在两个坐标轴上的截距的绝对值相等的直线有几条? 解得:a=b=3或a=-b=-1直线方程为:y+x-3=0、y-x-1=0或y=2x设 例4:已知三角形的三个顶点是A(-5,0), B(3,-3),C(0,2),求BC边所在的直线 方程,以及该边上中线的直线方程。解:过B(3,-3),C(0,2)两点式方程为:整理得:5x+3y-6=0这就是BC边所在直线的方程。五、直线方程的应用 BC边上的中线是顶点A与BC边中点M所连线段,由中点坐标公式可得点M的坐标为:即整理得:x+13y+5=0
这就是BC边上中线所在的直线的方程。 过A(-5,0),M 的直线方程中点坐标公式:
则 若P1 ,P2坐标分别为( x1 ,y1 ), (x2 ,y2)
且中点M的坐标为(x,y).∵B(3,-3),C(0,2)
∴ M 不垂直x轴不垂直x轴不垂直两个坐标轴不垂直两个坐标
轴且不经过原点各类方程的适用范围灵活选取方程的形式来求方程补充例题: 根据下列条件,写出直线的方程(1)倾斜角为30°,经过A(8,-2);(2)经过点B(-2,0),且与x轴垂直;(3)斜率为-4,在y轴上的截距为7;(4)经过点A(-1,8),B(4,-2);(5)在y轴上的截距是2,且与x轴平行;(6)在x轴,y轴上的截距分别是4,-3;1、求过点P( 2, 1)的直线与两坐标轴正半轴所围成的三角形的面积最小时的直线方程补充练习 2、已知两点A(-3,4),B(3, 2),过点P(2,-1)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围
(2)求直线l的倾斜角α的取值范围补充练习思考题: 已知直线l 2x+y+3=0,求关于点A(1,2)对称的直线l 1的方程。 解:当x=0时,y=-3.
(0,-3)在直线l上,关于(1,2)的对称点为(2,7). 当x=-2时,y=1.
(-2,1)在直线l上,关于(1,2)的对称点为(4,3).
那么,点 (2,7) ,(4,3)在l 1上因此,直线l 1的方程为:化简得: 2x + y -11=0还有其它的方法吗?∵ l ∥l 1,所以l 与l 1的斜率相同,∴ kl1=-2经计算,l 1过点(4,3)所以直线的点斜式方程为:y-3=-2(x-4)化简得: 2x + y -11=03)中点坐标:课堂总结:1)直线的两点式方程2)两点式直线方程的适应范围4)直线的截距式方程:5)截距式直线方程的适应范围课后作业:
P97练习:1,2.(做书上)
P100习题3.2A组:3,4,8,9.
