北师大版八年级数学下册 第三章 名校优选检测题【含答案】
文档属性
| 名称 | 北师大版八年级数学下册 第三章 名校优选检测题【含答案】 |  | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 10:29:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版八年级数学下册 第三章 名校优选检测题
(满分120分,考试用时120分钟)
姓名:________ 班级:________ 分数:________
一、选择题(每小题3分,共30分)
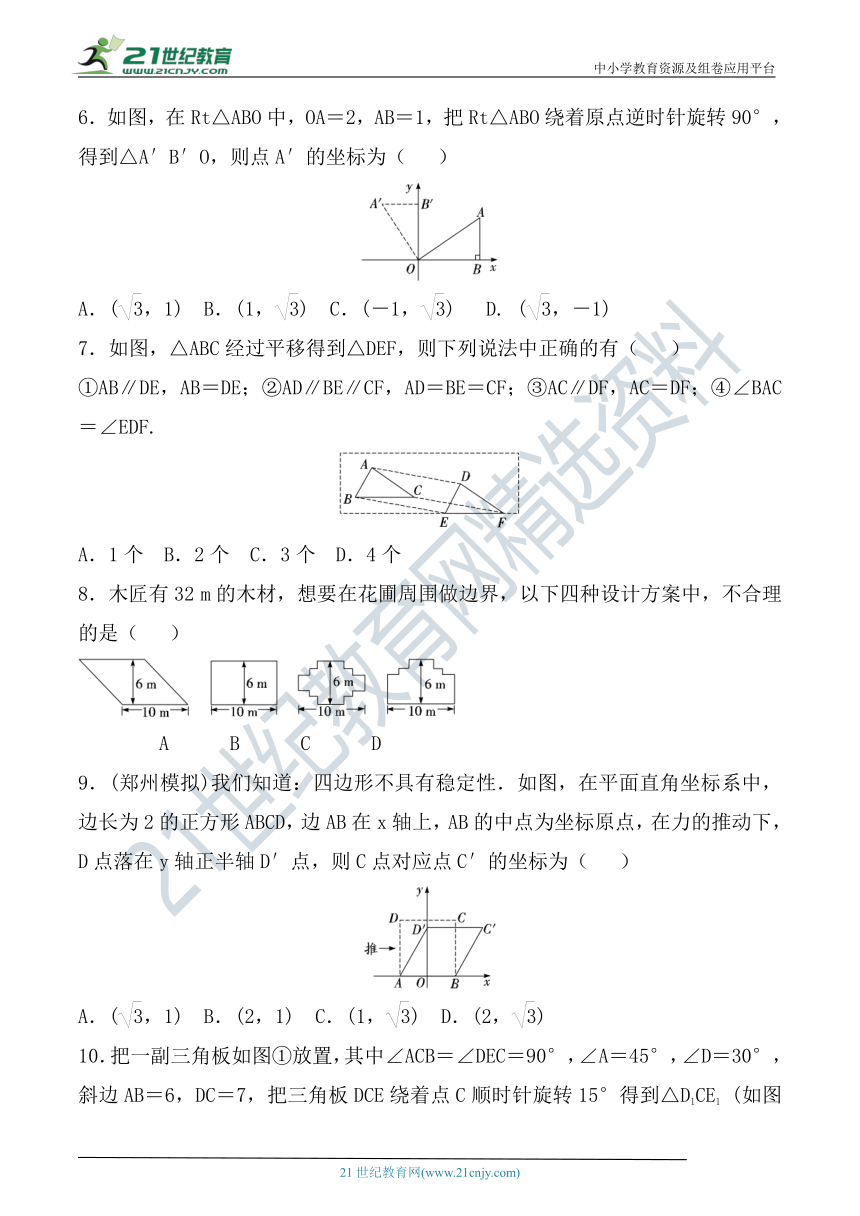
1.下列我国著名企业商标图案中,是中心对称图形的是( )
A B C D
2.把点A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到点B,则点B的坐标是( )
A.(15,3) B.(1,3) C.(1,-3) D.(-5,-1)
3.如图,在4×6方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.格点M B.格点N C.格点P D.格点Q
4.如图,将正方形图案绕中心O旋转180°后,得到的图案是( )
A B C D
5.(天津中考)如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD.则下列结论中一定正确的是( )
A.∠ABC=∠E B.∠CBE=∠C C.AD∥BC D.AD=BC
6.如图,在Rt△ABO中,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得到△A′B′O,则点A′的坐标为( )
A.(,1) B.(1,) C.(-1,) D. (,-1)
7.如图,△ABC经过平移得到△DEF,则下列说法中正确的有( )
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;③AC∥DF,AC=DF;④∠BAC=∠EDF.
A.1个 B.2个 C.3个 D.4个
8.木匠有32 m的木材,想要在花圃周围做边界,以下四种设计方案中,不合理的是( )
A B C D
9.(郑州模拟)我们知道:四边形不具有稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD,边AB在x轴上,AB的中点为坐标原点,在力的推动下,D点落在y轴正半轴D′点,则C点对应点C′的坐标为( )
A.(,1) B.(2,1) C.(1,) D.(2,)
10.把一副三角板如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1 (如图②),此时AB与CD1交于点O,则线段AD1的长度为( )
A.3 B.5 C.4 D.
二、填空题(每小题3分,共24分)
11.点A(2,1)与点B关于原点对称,则点B的坐标是 .
12.将点P(x,2)向右平移3个单位长度,再向上平移2个单位长度得到点Q(6,y),则x= ,y= .
13.如图所示的四个图形中,图①与图 可通过平移而相互得到;图①与图 可通过旋转而相互得到;图①与图 可通过作轴对称图形而相互得到.
① ② ③ ④
14.如图,△ABC,△ACD,△ADE是三个全等的正三角形,那么△ABC绕着顶点A沿逆时针方向至少旋转 ,才能与△ADE完全重合.
15.(南关区期末)如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D,若OB=5,OD=3,则阴影部分的面积之和为 .
如图,在正方形网格中,阴影部分是涂黑7个小正方形所形成的图案,再将网格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法
有 种.
17.如图,在△ABC中,∠BAC=115°,∠ACB=25°,把△ABC以AC为对称轴作对称变换得△ADC,又把△ABC绕点B逆时针旋转55°得△FBE,则∠α的度数为 .
18.如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2 022的直角顶点坐标为 .
三、解答题(共66分)
19.(8分)利用平移、旋转或轴对称分析图中图案的形成过程.
20.(10分)如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
(1)分别写出△DEF各顶点的坐标;
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
21.(12分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.
(1)若AC=4,求DE的值;
(2)确定△ACD的形状,并说明理由.
22.(12分)如图,在△ABC中,AD是BC边上的中线.
(1)以D为对称中心,画出与△ACD成中心对称的图形;
(2)若AB=5,AC=3,求中线AD的取值范围.
23.(12分)(1)如图①,在方格纸中(每个小正方形的边长均为1个单位长度)如何通过平移或旋转这两种变换,由图形A得到图形B,再由图形B得到图形C
(2)如图①,如果点P,P3的坐标分别为(0,0),(2,1),写出点P2的坐标;
(3)如图②是某设计师设计的图案的一部分,请运用旋转变换的方法,在方格纸中将图形绕点O顺时针依次旋转90°,180°,270°,依次画出旋转后得到的图形.
24.(12分)如图,小明将一张长方形纸片沿对角线剪开,得到两张三角形纸片(如图②),量得它们的斜边长为10 cm,较小的锐角为30°,再将这两张三角形纸片摆成如图③的形状,且点B,C,F,D在同一条直线上,且点C与点F重合(在图③至图⑥中统一用F表示).小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请帮忙解决:
(1)将图③中的△ABF沿BD向右平移到图④的位置,使点B与点F重合,请求出平移的距离;
(2)将图③中的△ABF绕点F按顺时针方向旋转30°到图⑤的位置,A1F交DE于点G,请求出线段FG的长度;
(3)将图③中的△ABF沿直线AF翻折到图⑥的位置,AB1交DE于点H,求证:AH=DH.
参考答案
一、选择题(每小题3分,共30分)
1.下列我国著名企业商标图案中,是中心对称图形的是(B)
A B C D
2.把点A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到点B,则点B的坐标是(B)
A.(15,3) B.(1,3) C.(1,-3) D.(-5,-1)
3.如图,在4×6方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是(B)
A.格点M B.格点N C.格点P D.格点Q
4.如图,将正方形图案绕中心O旋转180°后,得到的图案是(C)
A B C D
5.(天津中考)如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD.则下列结论中一定正确的是(C)
A.∠ABC=∠E B.∠CBE=∠C C.AD∥BC D.AD=BC
6.如图,在Rt△ABO中,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得到△A′B′O,则点A′的坐标为(C)
A.(,1) B.(1,) C.(-1,) D. (,-1)
7.如图,△ABC经过平移得到△DEF,则下列说法中正确的有(D)
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;③AC∥DF,AC=DF;④∠BAC=∠EDF.
A.1个 B.2个 C.3个 D.4个
8.木匠有32 m的木材,想要在花圃周围做边界,以下四种设计方案中,不合理的是(A)
A B C D
9.(郑州模拟)我们知道:四边形不具有稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD,边AB在x轴上,AB的中点为坐标原点,在力的推动下,D点落在y轴正半轴D′点,则C点对应点C′的坐标为(D)
A.(,1) B.(2,1) C.(1,) D.(2,)
10.把一副三角板如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1 (如图②),此时AB与CD1交于点O,则线段AD1的长度为(B)
A.3 B.5 C.4 D.
二、填空题(每小题3分,共24分)
11.点A(2,1)与点B关于原点对称,则点B的坐标是(-2,-1).
12.将点P(x,2)向右平移3个单位长度,再向上平移2个单位长度得到点Q(6,y),则x=3,y=4.
13.如图所示的四个图形中,图①与图②可通过平移而相互得到;图①与图③可通过旋转而相互得到;图①与图④可通过作轴对称图形而相互得到.
① ② ③ ④
14.如图,△ABC,△ACD,△ADE是三个全等的正三角形,那么△ABC绕着顶点A沿逆时针方向至少旋转120°,才能与△ADE完全重合.
15.(南关区期末)如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D,若OB=5,OD=3,则阴影部分的面积之和为15.
16.如图,在正方形网格中,阴影部分是涂黑7个小正方形所形成的图案,再将网格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有3种.
17.如图,在△ABC中,∠BAC=115°,∠ACB=25°,把△ABC以AC为对称轴作对称变换得△ADC,又把△ABC绕点B逆时针旋转55°得△FBE,则∠α的度数为145°.
18.如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2 022的直角顶点坐标为(8 088,0).
【解析】根据勾股定理列式求出AB的长,再根据第四个三角形与第一个三角形的位置相同可知每三个三角形为一个循环组依次循环,然后求出一个循环组旋转前进的长度,再用2 022除以3,根据商为674,可知第2 022个三角形的直角顶点为循环组的最后一个三角形的顶点,求出即可.
三、解答题(共66分)
19.(8分)利用平移、旋转或轴对称分析图中图案的形成过程.
解:以半个“蝴蝶形”为“基本图案”,通过轴对称得到一个“蝴蝶形”,再以这个“蝴蝶形”对称轴上一点为旋转中心旋转180°后通过平移得到另一个“蝴蝶形”,再将这两个“蝴蝶形”作为一个整体.沿水平方向连续平移2次便可得到题目中的图案.
20.(10分)如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
(1)分别写出△DEF各顶点的坐标;
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
解:(1)D(2,9),E(1,5),F(4,6).
(2)连接AD,由图可知AD==5,
∴如果将△DEF看成是由△ABC经过一次平移得到的,那么这一平移的平移方向是由A到D的方向,平移的距离是5个单位长度.
21.(12分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.
(1)若AC=4,求DE的值;
(2)确定△ACD的形状,并说明理由.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,AC=4,∴AB=2AC=8.
∵将△ABC绕点C顺时针旋转一定角度得到△DEC,
∴DE=AB=8.
(2)△ACD是等边三角形,理由:∵∠ACB=90°,∠B=30°,
∴∠A=180°-∠ACB-∠B=180°-90°-30=60°.
∵将△ABC绕点C顺时针旋转一定角度得到△DEC,
∴AC=CD.∴△ACD是等边三角形.
22.(12分)如图,在△ABC中,AD是BC边上的中线.
(1)以D为对称中心,画出与△ACD成中心对称的图形;
(2)若AB=5,AC=3,求中线AD的取值范围.
解:(1)如图,△EBD与△ACD成中心对称.
(2)由对称得AD=ED,BE=AC=3.
∵AB=5,BE=3,∴AB-BE<AE<AB+BE,∴2<AE<8.
∴1<AD<4.
23.(12分)(1)如图①,在方格纸中(每个小正方形的边长均为1个单位长度)如何通过平移或旋转这两种变换,由图形A得到图形B,再由图形B得到图形C
(2)如图①,如果点P,P3的坐标分别为(0,0),(2,1),写出点P2的坐标;
(3)如图②是某设计师设计的图案的一部分,请运用旋转变换的方法,在方格纸中将图形绕点O顺时针依次旋转90°,180°,270°,依次画出旋转后得到的图形.
解:(1)将图形A向上平移4个单位长度,得到图形B;将图形B以点P1为旋转中心顺时针旋转90°,再向右平移4个单位长度得到图形C(或将图形B向右平移4个单位长度,再以P2为旋转中心顺时针旋转90°得到图形C).
(2)∵点P,P3的坐标分别为(0,0),(2,1),∴P2(4,4).
(3)如图②.
24.(12分)如图,小明将一张长方形纸片沿对角线剪开,得到两张三角形纸片(如图②),量得它们的斜边长为10 cm,较小的锐角为30°,再将这两张三角形纸片摆成如图③的形状,且点B,C,F,D在同一条直线上,且点C与点F重合(在图③至图⑥中统一用F表示).小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请帮忙解决:
(1)将图③中的△ABF沿BD向右平移到图④的位置,使点B与点F重合,请求出平移的距离;
(2)将图③中的△ABF绕点F按顺时针方向旋转30°到图⑤的位置,A1F交DE于点G,请求出线段FG的长度;
(3)将图③中的△ABF沿直线AF翻折到图⑥的位置,AB1交DE于点H,求证:AH=DH.
(1)解:图形平移的距离就是线段BF的长,
∵Rt△ABF中,斜边长为10 cm,∠BAF=30°,
∴BF=5 cm,∴平移的距离为5 cm.
(2)解:∵∠A1FA=30°,∴∠GFD=60°,
又∵∠D=30°,∴∠FGD=90°.
∵DE=10 cm,EF=DE=5 cm,
∴由勾股定理得DF=5 cm,
∴在Rt△DFG中,
FG=FD= cm.
(3)证明:∵FD=FA,EF=FB=FB1,
∴FD-FB1=FA-FE,即AE=DB1.
又∵在△AHE与△DHB1中,
∠FAB1=∠EDF=30°,∠AHE=∠DHB1.
∴△AHE≌△DHB1(AAS),∴AH=DH.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版八年级数学下册 第三章 名校优选检测题
(满分120分,考试用时120分钟)
姓名:________ 班级:________ 分数:________
一、选择题(每小题3分,共30分)
1.下列我国著名企业商标图案中,是中心对称图形的是( )
A B C D
2.把点A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到点B,则点B的坐标是( )
A.(15,3) B.(1,3) C.(1,-3) D.(-5,-1)
3.如图,在4×6方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.格点M B.格点N C.格点P D.格点Q
4.如图,将正方形图案绕中心O旋转180°后,得到的图案是( )
A B C D
5.(天津中考)如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD.则下列结论中一定正确的是( )
A.∠ABC=∠E B.∠CBE=∠C C.AD∥BC D.AD=BC
6.如图,在Rt△ABO中,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得到△A′B′O,则点A′的坐标为( )
A.(,1) B.(1,) C.(-1,) D. (,-1)
7.如图,△ABC经过平移得到△DEF,则下列说法中正确的有( )
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;③AC∥DF,AC=DF;④∠BAC=∠EDF.
A.1个 B.2个 C.3个 D.4个
8.木匠有32 m的木材,想要在花圃周围做边界,以下四种设计方案中,不合理的是( )
A B C D
9.(郑州模拟)我们知道:四边形不具有稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD,边AB在x轴上,AB的中点为坐标原点,在力的推动下,D点落在y轴正半轴D′点,则C点对应点C′的坐标为( )
A.(,1) B.(2,1) C.(1,) D.(2,)
10.把一副三角板如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1 (如图②),此时AB与CD1交于点O,则线段AD1的长度为( )
A.3 B.5 C.4 D.
二、填空题(每小题3分,共24分)
11.点A(2,1)与点B关于原点对称,则点B的坐标是 .
12.将点P(x,2)向右平移3个单位长度,再向上平移2个单位长度得到点Q(6,y),则x= ,y= .
13.如图所示的四个图形中,图①与图 可通过平移而相互得到;图①与图 可通过旋转而相互得到;图①与图 可通过作轴对称图形而相互得到.
① ② ③ ④
14.如图,△ABC,△ACD,△ADE是三个全等的正三角形,那么△ABC绕着顶点A沿逆时针方向至少旋转 ,才能与△ADE完全重合.
15.(南关区期末)如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D,若OB=5,OD=3,则阴影部分的面积之和为 .
如图,在正方形网格中,阴影部分是涂黑7个小正方形所形成的图案,再将网格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法
有 种.
17.如图,在△ABC中,∠BAC=115°,∠ACB=25°,把△ABC以AC为对称轴作对称变换得△ADC,又把△ABC绕点B逆时针旋转55°得△FBE,则∠α的度数为 .
18.如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2 022的直角顶点坐标为 .
三、解答题(共66分)
19.(8分)利用平移、旋转或轴对称分析图中图案的形成过程.
20.(10分)如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
(1)分别写出△DEF各顶点的坐标;
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
21.(12分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.
(1)若AC=4,求DE的值;
(2)确定△ACD的形状,并说明理由.
22.(12分)如图,在△ABC中,AD是BC边上的中线.
(1)以D为对称中心,画出与△ACD成中心对称的图形;
(2)若AB=5,AC=3,求中线AD的取值范围.
23.(12分)(1)如图①,在方格纸中(每个小正方形的边长均为1个单位长度)如何通过平移或旋转这两种变换,由图形A得到图形B,再由图形B得到图形C
(2)如图①,如果点P,P3的坐标分别为(0,0),(2,1),写出点P2的坐标;
(3)如图②是某设计师设计的图案的一部分,请运用旋转变换的方法,在方格纸中将图形绕点O顺时针依次旋转90°,180°,270°,依次画出旋转后得到的图形.
24.(12分)如图,小明将一张长方形纸片沿对角线剪开,得到两张三角形纸片(如图②),量得它们的斜边长为10 cm,较小的锐角为30°,再将这两张三角形纸片摆成如图③的形状,且点B,C,F,D在同一条直线上,且点C与点F重合(在图③至图⑥中统一用F表示).小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请帮忙解决:
(1)将图③中的△ABF沿BD向右平移到图④的位置,使点B与点F重合,请求出平移的距离;
(2)将图③中的△ABF绕点F按顺时针方向旋转30°到图⑤的位置,A1F交DE于点G,请求出线段FG的长度;
(3)将图③中的△ABF沿直线AF翻折到图⑥的位置,AB1交DE于点H,求证:AH=DH.
参考答案
一、选择题(每小题3分,共30分)
1.下列我国著名企业商标图案中,是中心对称图形的是(B)
A B C D
2.把点A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到点B,则点B的坐标是(B)
A.(15,3) B.(1,3) C.(1,-3) D.(-5,-1)
3.如图,在4×6方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是(B)
A.格点M B.格点N C.格点P D.格点Q
4.如图,将正方形图案绕中心O旋转180°后,得到的图案是(C)
A B C D
5.(天津中考)如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD.则下列结论中一定正确的是(C)
A.∠ABC=∠E B.∠CBE=∠C C.AD∥BC D.AD=BC
6.如图,在Rt△ABO中,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得到△A′B′O,则点A′的坐标为(C)
A.(,1) B.(1,) C.(-1,) D. (,-1)
7.如图,△ABC经过平移得到△DEF,则下列说法中正确的有(D)
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;③AC∥DF,AC=DF;④∠BAC=∠EDF.
A.1个 B.2个 C.3个 D.4个
8.木匠有32 m的木材,想要在花圃周围做边界,以下四种设计方案中,不合理的是(A)
A B C D
9.(郑州模拟)我们知道:四边形不具有稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD,边AB在x轴上,AB的中点为坐标原点,在力的推动下,D点落在y轴正半轴D′点,则C点对应点C′的坐标为(D)
A.(,1) B.(2,1) C.(1,) D.(2,)
10.把一副三角板如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1 (如图②),此时AB与CD1交于点O,则线段AD1的长度为(B)
A.3 B.5 C.4 D.
二、填空题(每小题3分,共24分)
11.点A(2,1)与点B关于原点对称,则点B的坐标是(-2,-1).
12.将点P(x,2)向右平移3个单位长度,再向上平移2个单位长度得到点Q(6,y),则x=3,y=4.
13.如图所示的四个图形中,图①与图②可通过平移而相互得到;图①与图③可通过旋转而相互得到;图①与图④可通过作轴对称图形而相互得到.
① ② ③ ④
14.如图,△ABC,△ACD,△ADE是三个全等的正三角形,那么△ABC绕着顶点A沿逆时针方向至少旋转120°,才能与△ADE完全重合.
15.(南关区期末)如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D,若OB=5,OD=3,则阴影部分的面积之和为15.
16.如图,在正方形网格中,阴影部分是涂黑7个小正方形所形成的图案,再将网格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有3种.
17.如图,在△ABC中,∠BAC=115°,∠ACB=25°,把△ABC以AC为对称轴作对称变换得△ADC,又把△ABC绕点B逆时针旋转55°得△FBE,则∠α的度数为145°.
18.如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2 022的直角顶点坐标为(8 088,0).
【解析】根据勾股定理列式求出AB的长,再根据第四个三角形与第一个三角形的位置相同可知每三个三角形为一个循环组依次循环,然后求出一个循环组旋转前进的长度,再用2 022除以3,根据商为674,可知第2 022个三角形的直角顶点为循环组的最后一个三角形的顶点,求出即可.
三、解答题(共66分)
19.(8分)利用平移、旋转或轴对称分析图中图案的形成过程.
解:以半个“蝴蝶形”为“基本图案”,通过轴对称得到一个“蝴蝶形”,再以这个“蝴蝶形”对称轴上一点为旋转中心旋转180°后通过平移得到另一个“蝴蝶形”,再将这两个“蝴蝶形”作为一个整体.沿水平方向连续平移2次便可得到题目中的图案.
20.(10分)如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
(1)分别写出△DEF各顶点的坐标;
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
解:(1)D(2,9),E(1,5),F(4,6).
(2)连接AD,由图可知AD==5,
∴如果将△DEF看成是由△ABC经过一次平移得到的,那么这一平移的平移方向是由A到D的方向,平移的距离是5个单位长度.
21.(12分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好在AB上.
(1)若AC=4,求DE的值;
(2)确定△ACD的形状,并说明理由.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,AC=4,∴AB=2AC=8.
∵将△ABC绕点C顺时针旋转一定角度得到△DEC,
∴DE=AB=8.
(2)△ACD是等边三角形,理由:∵∠ACB=90°,∠B=30°,
∴∠A=180°-∠ACB-∠B=180°-90°-30=60°.
∵将△ABC绕点C顺时针旋转一定角度得到△DEC,
∴AC=CD.∴△ACD是等边三角形.
22.(12分)如图,在△ABC中,AD是BC边上的中线.
(1)以D为对称中心,画出与△ACD成中心对称的图形;
(2)若AB=5,AC=3,求中线AD的取值范围.
解:(1)如图,△EBD与△ACD成中心对称.
(2)由对称得AD=ED,BE=AC=3.
∵AB=5,BE=3,∴AB-BE<AE<AB+BE,∴2<AE<8.
∴1<AD<4.
23.(12分)(1)如图①,在方格纸中(每个小正方形的边长均为1个单位长度)如何通过平移或旋转这两种变换,由图形A得到图形B,再由图形B得到图形C
(2)如图①,如果点P,P3的坐标分别为(0,0),(2,1),写出点P2的坐标;
(3)如图②是某设计师设计的图案的一部分,请运用旋转变换的方法,在方格纸中将图形绕点O顺时针依次旋转90°,180°,270°,依次画出旋转后得到的图形.
解:(1)将图形A向上平移4个单位长度,得到图形B;将图形B以点P1为旋转中心顺时针旋转90°,再向右平移4个单位长度得到图形C(或将图形B向右平移4个单位长度,再以P2为旋转中心顺时针旋转90°得到图形C).
(2)∵点P,P3的坐标分别为(0,0),(2,1),∴P2(4,4).
(3)如图②.
24.(12分)如图,小明将一张长方形纸片沿对角线剪开,得到两张三角形纸片(如图②),量得它们的斜边长为10 cm,较小的锐角为30°,再将这两张三角形纸片摆成如图③的形状,且点B,C,F,D在同一条直线上,且点C与点F重合(在图③至图⑥中统一用F表示).小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请帮忙解决:
(1)将图③中的△ABF沿BD向右平移到图④的位置,使点B与点F重合,请求出平移的距离;
(2)将图③中的△ABF绕点F按顺时针方向旋转30°到图⑤的位置,A1F交DE于点G,请求出线段FG的长度;
(3)将图③中的△ABF沿直线AF翻折到图⑥的位置,AB1交DE于点H,求证:AH=DH.
(1)解:图形平移的距离就是线段BF的长,
∵Rt△ABF中,斜边长为10 cm,∠BAF=30°,
∴BF=5 cm,∴平移的距离为5 cm.
(2)解:∵∠A1FA=30°,∴∠GFD=60°,
又∵∠D=30°,∴∠FGD=90°.
∵DE=10 cm,EF=DE=5 cm,
∴由勾股定理得DF=5 cm,
∴在Rt△DFG中,
FG=FD= cm.
(3)证明:∵FD=FA,EF=FB=FB1,
∴FD-FB1=FA-FE,即AE=DB1.
又∵在△AHE与△DHB1中,
∠FAB1=∠EDF=30°,∠AHE=∠DHB1.
∴△AHE≌△DHB1(AAS),∴AH=DH.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
