2021-2022学年重庆市沙坪坝区重点学校八年级(下)开学数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年重庆市沙坪坝区重点学校八年级(下)开学数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 16:46:31 | ||
图片预览


文档简介
2021-2022学年重庆市沙坪坝区重点学校八年级(下)开学数学试卷
一、选择题(本大题10个小题,每小题4分,共40分).
1.下列各数中,是无理数的是( )
A.2 B. C. D.
2.下列图形中,是中心对称图形的是( )
A. B. C. D.
3.计算(3a3)2的结果是( )
A.9a6 B.9a5 C.6a6 D.6a5
4.若x>y,则下列不等式一定成立的是( )
A.﹣x>﹣y B.2x<2y C. D.x+4>y+4
5.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AB=CD B.AB=CD,AD=BC
C.AB∥CD,∠B=∠D D.AB∥CD,AD=BC
6.如图所示,在平行四边形ABCD中,已知AB=8,AD=3,AE平分∠BAD交DC于点E,则CE的长为( )
A.3 B.4 C.5 D.8
7.估计×﹣4的值应该在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
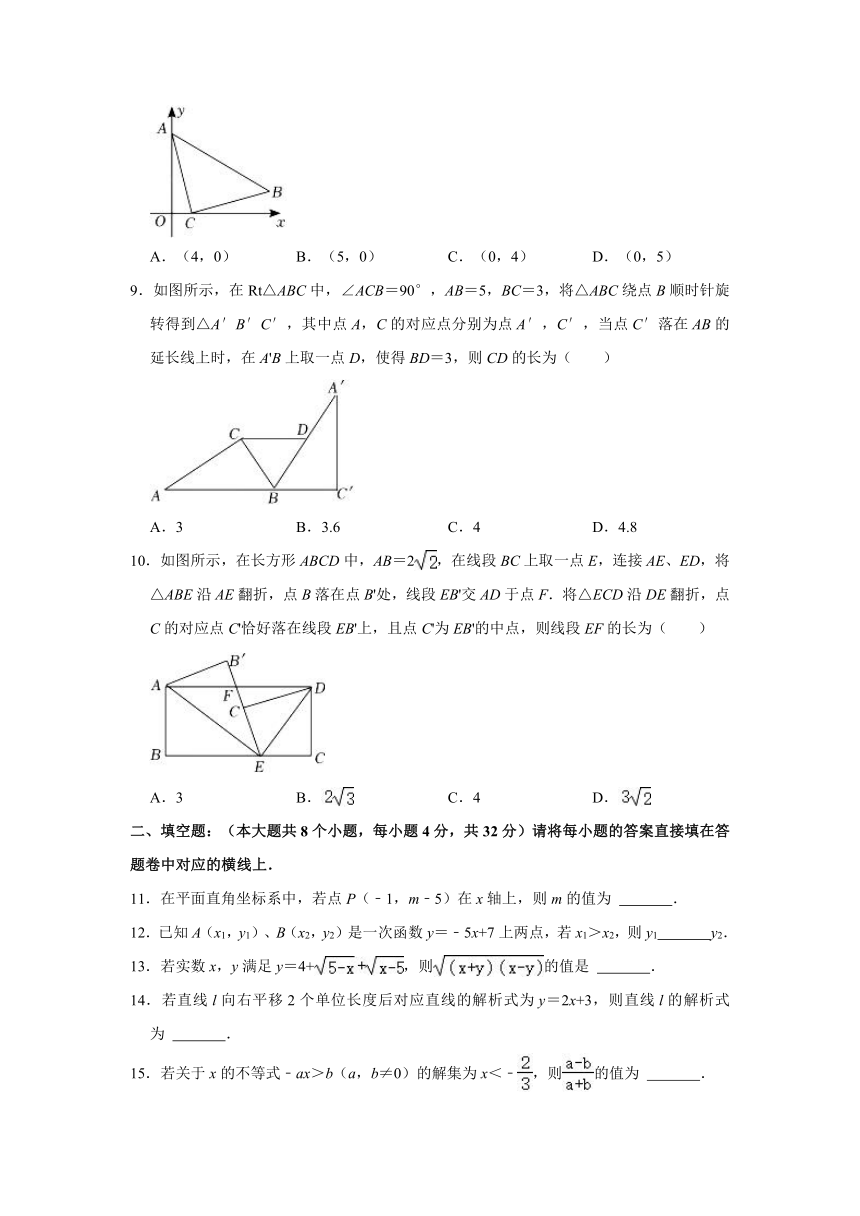
8.如图所示,在平面直角坐标系中,等腰Rt△ABC的直角顶点C在x轴上,点A在y轴上,若点B坐标为(6,1),则点A坐标为( )
A.(4,0) B.(5,0) C.(0,4) D.(0,5)
9.如图所示,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′B′C′,其中点A,C的对应点分别为点A′,C′,当点C′落在AB的延长线上时,在A'B上取一点D,使得BD=3,则CD的长为( )
A.3 B.3.6 C.4 D.4.8
10.如图所示,在长方形ABCD中,AB=2,在线段BC上取一点E,连接AE、ED,将△ABE沿AE翻折,点B落在点B'处,线段EB'交AD于点F.将△ECD沿DE翻折,点C的对应点C'恰好落在线段EB'上,且点C'为EB'的中点,则线段EF的长为( )
A.3 B. C.4 D.
二、填空题:(本大题共8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卷中对应的横线上.
11.在平面直角坐标系中,若点P(﹣1,m﹣5)在x轴上,则m的值为 .
12.已知A(x1,y1)、B(x2,y2)是一次函数y=﹣5x+7上两点,若x1>x2,则y1 y2.
13.若实数x,y满足y=4+,则的值是 .
14.若直线l向右平移2个单位长度后对应直线的解析式为y=2x+3,则直线l的解析式为 .
15.若关于x的不等式﹣ax>b(a,b≠0)的解集为x<﹣,则的值为 .
16.若整数a使关于x的一次函数y=﹣x+a﹣2不经过第三象限,且使关于y的不等式组有且仅有4个整数解,则所有满足条件的整数a的值之和为 .
17.如图,将平行四边形ABCD绕点D顺时针旋转150°得到四边形EFGD,这时点C,E,G恰好在同一直线上,延长AD交CG于点H.若AD=2,∠A=75°,则HG= .
18.为迎接北京冬奥会,在A、B两个社区共设置六个摊点售卖冬奥纪念品,其中第一、二、三号摊点在A社区,第四、五、六号摊点在B社区,每个摊点原有纪念品一样多.第一、二、三、四号摊点每天新运来相等数量的纪念品,第五号摊点每天新运来的纪念品数量是前四个摊点每天新增总量的,第六号摊点每天新运来的纪念品数量是前四个摊点每天新增总量的.第3天结束营业时,第四、五号摊点的纪念品恰好售完并撤走摊点;第4天结束营业时,第一、二、三、六号摊点的所有纪念品均售完并撤走.若第四号和第六号摊点平均每天售出的纪念品数量相等,则A、B两社区售出纪念品的总数量之比为 .
三、解答题:(本大题3个小题,19题8分,20、21题各10分,共28分)解答时每小题必须给出演算过程或推理步骤.
19.计算:
(1)|﹣1|﹣(π﹣2)0+(﹣)﹣2;
(2)(6﹣)÷.
20.解方程组:
(1);
(2).
21.解不等式(组):
(1)4(x﹣2)+7<3;
(2).
四、解答题:(本大题5个小题,每小题10分,共50分)解答时每小题必须给出必要的演算过程或步骤.
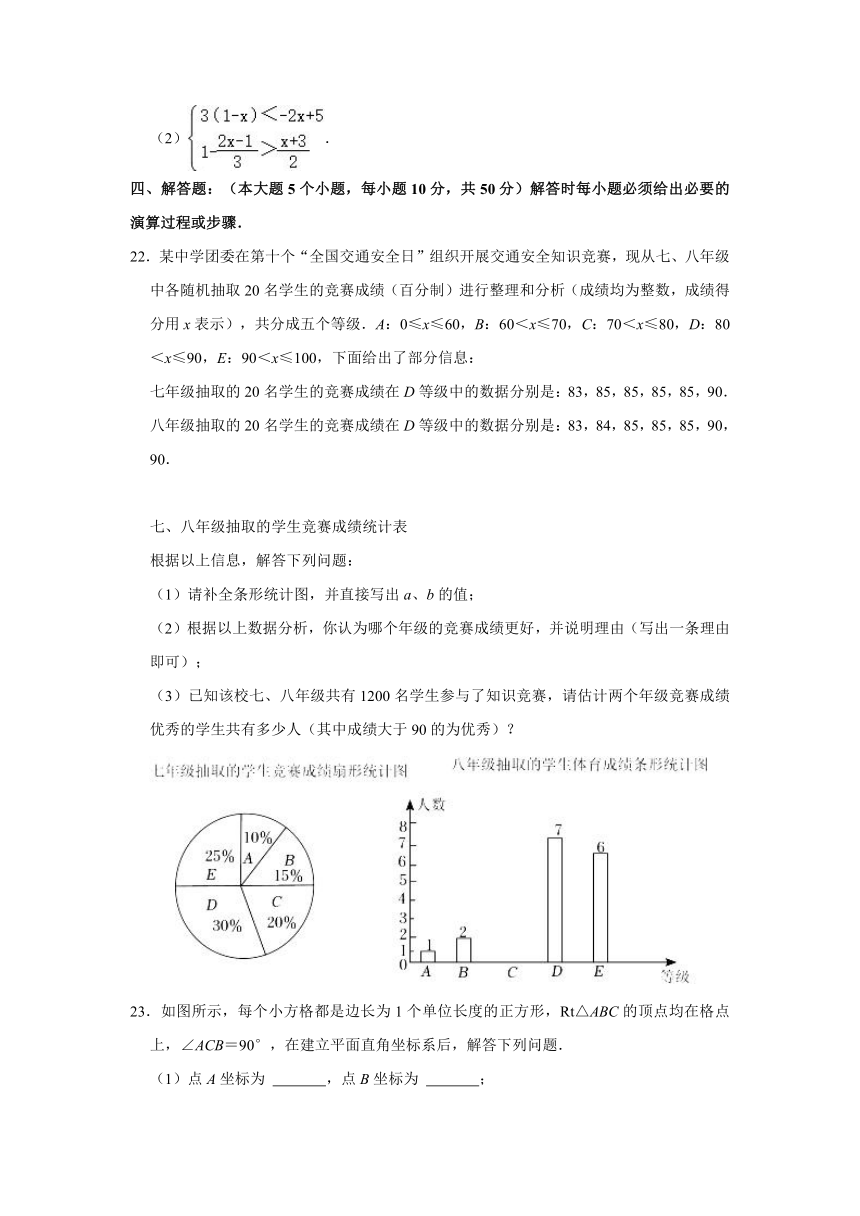
22.某中学团委在第十个“全国交通安全日”组织开展交通安全知识竞赛,现从七、八年级中各随机抽取20名学生的竞赛成绩(百分制)进行整理和分析(成绩均为整数,成绩得分用x表示),共分成五个等级.A:0≤x≤60,B:60<x≤70,C:70<x≤80,D:80<x≤90,E:90<x≤100,下面给出了部分信息:
七年级抽取的20名学生的竞赛成绩在D等级中的数据分别是:83,85,85,85,85,90.
八年级抽取的20名学生的竞赛成绩在D等级中的数据分别是:83,84,85,85,85,90,90.
七、八年级抽取的学生竞赛成绩统计表
根据以上信息,解答下列问题:
(1)请补全条形统计图,并直接写出a、b的值;
(2)根据以上数据分析,你认为哪个年级的竞赛成绩更好,并说明理由(写出一条理由即可);
(3)已知该校七、八年级共有1200名学生参与了知识竞赛,请估计两个年级竞赛成绩优秀的学生共有多少人(其中成绩大于90的为优秀)?
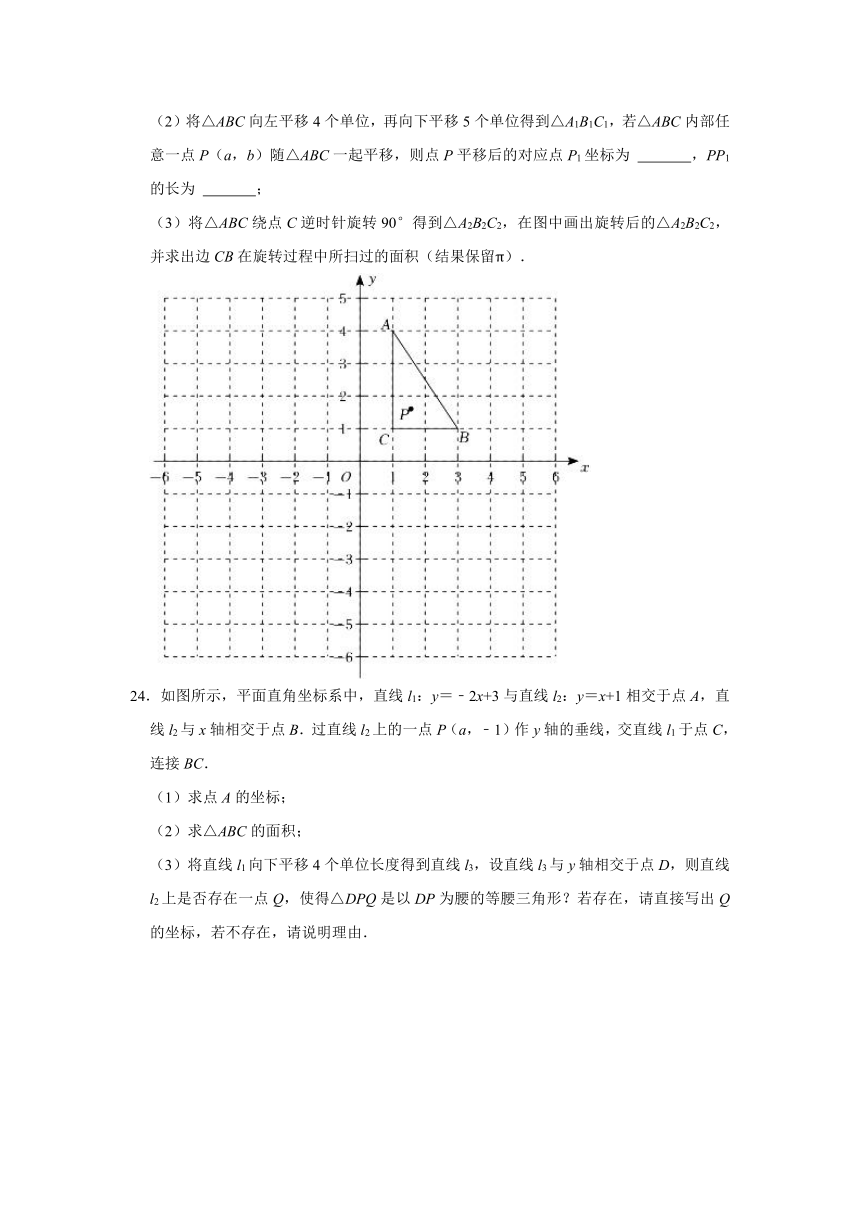
23.如图所示,每个小方格都是边长为1个单位长度的正方形,Rt△ABC的顶点均在格点上,∠ACB=90°,在建立平面直角坐标系后,解答下列问题.
(1)点A坐标为 ,点B坐标为 ;
(2)将△ABC向左平移4个单位,再向下平移5个单位得到△A1B1C1,若△ABC内部任意一点P(a,b)随△ABC一起平移,则点P平移后的对应点P1坐标为 ,PP1的长为 ;
(3)将△ABC绕点C逆时针旋转90°得到△A2B2C2,在图中画出旋转后的△A2B2C2,并求出边CB在旋转过程中所扫过的面积(结果保留π).
24.如图所示,平面直角坐标系中,直线l1:y=﹣2x+3与直线l2:y=x+1相交于点A,直线l2与x轴相交于点B.过直线l2上的一点P(a,﹣1)作y轴的垂线,交直线l1于点C,连接BC.
(1)求点A的坐标;
(2)求△ABC的面积;
(3)将直线l1向下平移4个单位长度得到直线l3,设直线l3与y轴相交于点D,则直线l2上是否存在一点Q,使得△DPQ是以DP为腰的等腰三角形?若存在,请直接写出Q的坐标,若不存在,请说明理由.
25.“红缬退风花著子,绿针浮水稻抽秧”这是宋朝诗人姚孝锡所作.诗中咏诵的“水稻”是我国种植的重要经济作物.某村在政府的扶持下建起了水稻种植基地,准备种植甲,乙两种水稻,若种植20亩甲种水稻和30亩乙种水稻,共需投入22万元;若种植30亩甲种水稻和20亩乙种水稻,共需投入23万元.
(1)种植甲,乙两种水稻,每亩各需投入多少万元?
(2)经测算,种植甲种水稻每亩可获利a(a>0且a为常数)万元,种植乙种水稻每亩可获利0.8万元,村里投入50万元用来种植这两种水稻,若要求甲种水稻的种植面积不能少于乙种水稻种植面积的倍,且不能多于乙种水稻种植面积的倍.设种植乙种水稻m亩,该村种植两种水稻共获利W万元,请求出W关于m的函数表达式,并求出最大获利(用含a的代数式表示).
26.在平行四边形ABCD中,连接BD,若BD⊥CD,点E为边AD上一点,连接CE.
(1)如图1,点G在BD上,且DG=DC,连接CG,过G作GH⊥CE于点H,连接DH并延长交AB于点M,若HG=BM,求证:BM+DH=DB;
(2)如图2,∠ABC=120°,AB=,点N在BC边上,BC=4CN,若CE是∠DCB的角平分线,线段PQ(点P在点Q的左侧)在线段CE上运动,PQ=,连接BP、NQ,请直接写出BP+PQ+QN的最小值.
参考答案
一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将正确答案填写在答题卷上对应的位置.
1.下列各数中,是无理数的是( )
A.2 B. C. D.
【分析】根据无理数是无限不循环小数,可得答案.
解:A、2是整数,属于有理数,故此选项不符合题意;
B、﹣是分数,属于有理数,故此选项不符合题意;
C、是无理数,故此选项符合题意;
D、是无限循环小数,属于有理数,故此选项不符合题意.
故选:C.
2.下列图形中,是中心对称图形的是( )
A. B. C. D.
【分析】根据中心对称图形的概念求解判断即可.
解:A.不是中心对称图形,故此选项不符合题意;
B.不是中心对称图形,故此选项不符合题意;
C.是中心对称图形,故此选项符合题意;
D.不是中心对称图形,故此选项不符合题意.
故选:C.
3.计算(3a3)2的结果是( )
A.9a6 B.9a5 C.6a6 D.6a5
【分析】根据幂的乘方与积的乘方法则进行计算即可得出结果.
解:(3a3)2=9(a3)2=9a6,
故选:A.
4.若x>y,则下列不等式一定成立的是( )
A.﹣x>﹣y B.2x<2y C. D.x+4>y+4
【分析】根据不等式的性质判断即可.
解:A.因为x>y,所以﹣x<﹣y,故A不符合题意;
B.因为x>y,所以2x>2y,故B不符合题意;
C.因为x>y,所以>,故C不符合题意;
D.因为x>y,所以x+4>y+4,故D符合题意;
故选:D.
5.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AB=CD B.AB=CD,AD=BC
C.AB∥CD,∠B=∠D D.AB∥CD,AD=BC
【分析】根据平行四边形的判定定理分别进行分析即可.
解:A、∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,故此选项不合题意;
B、∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,故此选项不合题意;
C、∵AB∥CD,∠B=∠D,∴四边形ABCD是平行四边形,故此选项不合题意;
D、∵AB∥CD,AD=BC,不能得出四边形ABCD是平行四边形,故此选项符合题意;
故选:D.
6.如图所示,在平行四边形ABCD中,已知AB=8,AD=3,AE平分∠BAD交DC于点E,则CE的长为( )
A.3 B.4 C.5 D.8
【分析】由平行四边形的性质得出BC=AD=5,AD∥BC,得出∠DAE=∠BEA,证出∠BEA=∠BAE,得出BE=AB,即可得出CE的长.
解:∵四边形ABCD是平行四边形,
∴CD=AB=8,AB∥DC,
∴∠BAE=∠DEA,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠DEA=∠DAE,
∴DE=AD=3,
∴CE=DC﹣CE=8﹣3=5;
故选:C.
7.估计×﹣4的值应该在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
【分析】先进行二次根式的混合运算,然后再估算出的值即可解答.
解:×﹣4
=5﹣4
=,
∵4<6<9,
∴2<<3,
∴估计×﹣4的值应该在:2和3之间,
故选:B.
8.如图所示,在平面直角坐标系中,等腰Rt△ABC的直角顶点C在x轴上,点A在y轴上,若点B坐标为(6,1),则点A坐标为( )
A.(4,0) B.(5,0) C.(0,4) D.(0,5)
【分析】作BD⊥x轴于D,证明△ACO≌△CBD(AAS),得OC=BD=1,CD=OA=5,从而解决问题.
解:作BD⊥x轴于D,
∵B(6,1),
∴BD=1,OD=6,
∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴∠ACO+∠BCD=90°,
∵∠ACO+∠OAC=90°,
∴∠BCD=∠OAC,
∵∠AOC=∠BDO,
∴△ACO≌△CBD(AAS),
∴OC=BD=1,CD=OA=5,
∴A(0,5),
故选:D.
9.如图所示,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′B′C′,其中点A,C的对应点分别为点A′,C′,当点C′落在AB的延长线上时,在A'B上取一点D,使得BD=3,则CD的长为( )
A.3 B.3.6 C.4 D.4.8
【分析】过B作BE⊥CD于E,根据△ABC绕点B顺时针旋转得到△A′BC′,可得∠ABC=∠A'BC',而BC=BD=3,可得∠BCD=∠BDC,由∠ABC+∠A'BC'+∠CBD=180°=∠BCD+∠BDC+∠CBD,即得∠ABC=∠BCD,故△ACB∽△BEC,可得=,CE=1.8,从而CD=2CE=3.6.
解:过B作BE⊥CD于E,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴∠ABC=∠A'BC',
∵BC=BD=3,
∴∠BCD=∠BDC,
∵∠ABC+∠A'BC'+∠CBD=180°=∠BCD+∠BDC+∠CBD,
∴∠ABC=∠BCD,
∵∠ACB=∠CEB=90°,
∴△ACB∽△BEC,
∴=,即=,
∴CE=1.8,
∵BC=BD,BE⊥CD,
∴CD=2CE=3.6,
故选:B.
10.如图所示,在长方形ABCD中,AB=2,在线段BC上取一点E,连接AE、ED,将△ABE沿AE翻折,点B落在点B'处,线段EB'交AD于点F.将△ECD沿DE翻折,点C的对应点C'恰好落在线段EB'上,且点C'为EB'的中点,则线段EF的长为( )
A.3 B. C.4 D.
【分析】由折叠的性质可得AB=AB'=CD=C'D=2,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,由中点性质可得B'E=2C'E,可得BC=AD=3EC,由勾股定理可求可求CE的长,由“AAS”可证△AB'F≌△DC'F,可得C'F=B'F=1,即可求解.
解:∵四边形ABCD是矩形,
∴AB=CD=1,AD=BC,∠B=∠C=90°
由折叠的性质可得:AB=AB'=CD=C'D=2,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,
∵点C'恰好为EB'的中点,
∴B'E=2C'E,
∴BE=2CE,
∴BC=AD=3EC,
∵AE2=AB2+BE2,DE2=DC2+CE2,AD2=AE2+DE2,
∴8+4CE2+8+CE2=9CE2,
∴CE=2,
∴B'E=BE=4,BC=AD=6,C'E=2,
∴B'C'=2,
∵∠B'=∠DC'F=90°,∠AFB'=∠DFC',AB'=C'D,
∴△AB'F≌△DC'F(AAS),
∴C'F=B'F=1,
∴EF=C'E+C'F=3,
故选:A.
二、填空题:(本大题共8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卷中对应的横线上.
11.在平面直角坐标系中,若点P(﹣1,m﹣5)在x轴上,则m的值为 5 .
【分析】根据x轴上点的纵坐标为0列方程求解即可.
解:∵点P(﹣1,m﹣5)在x轴上,
∴m﹣5=0,
解得m=5.
故答案为:5.
12.已知A(x1,y1)、B(x2,y2)是一次函数y=﹣5x+7上两点,若x1>x2,则y1 < y2.
【分析】由k=﹣2<0根据一次函数的性质可得出结论.
解:∵一次函数y=﹣5x+7中k=﹣5<0,
∴该一次函数y随x的增大而减小,
∵x1>x2,
∴y1<y2.
故答案为:<.
13.若实数x,y满足y=4+,则的值是 3 .
【分析】根据二次根式有意义的条件可得:,解出x的值,进而可得y的值,然后可得答案.
解:由题意得:,
解得:x=5,
则y=4,
===3,
故答案为:3.
14.若直线l向右平移2个单位长度后对应直线的解析式为y=2x+3,则直线l的解析式为 y=2x+7 .
【分析】直接根据“左加右减”的原则进行解答即可.
解:由“左加右减”的原则可知:把直线y=2x+3向左平移2个单位长度后,其直线l的解析式为y=2(x+2)+3,即y=2x+7.
故答案为:y=2x+7.
15.若关于x的不等式﹣ax>b(a,b≠0)的解集为x<﹣,则的值为 .
【分析】根据题意可得x<﹣,从而求出=,然后利用设k法进行计算即可解答.
解:由题意得:
x<﹣,
∵不等式解集为x<﹣,
∴=,
∴设b=2k,a=3k,
∴===,
故答案为:.
16.若整数a使关于x的一次函数y=﹣x+a﹣2不经过第三象限,且使关于y的不等式组有且仅有4个整数解,则所有满足条件的整数a的值之和为 5 .
【分析】由该一次函数不经过第三象限,可得a﹣2≥0,解得a≥2;解不等式组,并根据不等式有4个整数解,进而得出a的取值范围.
解:∵关于x的一次函数y=﹣x+a﹣2不经过第三象限,
∴a﹣2≥0,解得a≥2,
解关于y的不等式组,
解①得y≤2,解②得y>,
∵关于y的不等式组有且仅有4个整数解,
∴﹣2≤<﹣1,
解得1<a≤,
∴2≤a≤,
∵a为整数,
∴满足条件的a的值为2,3,
∴2+3=5,
故答案为:5.
17.如图,将平行四边形ABCD绕点D顺时针旋转150°得到四边形EFGD,这时点C,E,G恰好在同一直线上,延长AD交CG于点H.若AD=2,∠A=75°,则HG= 3+2 .
【分析】证明△CDG是顶角为150°的等腰三角形,再证明DH⊥CG,由直角三角形的性质求出DH,进而解决问题.
解:在CG上取一点K,使DK=GK,如图:
由题意:∠ADE=150°,AD=DE=2,
∴∠EDH=30°,
∵AB∥CD,
∴∠CDH=∠A=75°,
∵∠CDG=150°,DC=DG,
∴∠DGC=∠DCG=15°,∠CDH=∠GDH=75°,
∴DH⊥CG,
∴EH=DE=1,DH=EH=,
∵DK=GK,
∴∠KDG=∠KGD=15°,
∴∠DKH=15°+15°=30°,
∴KG=DK=2DH=2,HK=DH=3,
∴HG=HK+KG=3+2,
故答案为:3+2.
18.为迎接北京冬奥会,在A、B两个社区共设置六个摊点售卖冬奥纪念品,其中第一、二、三号摊点在A社区,第四、五、六号摊点在B社区,每个摊点原有纪念品一样多.第一、二、三、四号摊点每天新运来相等数量的纪念品,第五号摊点每天新运来的纪念品数量是前四个摊点每天新增总量的,第六号摊点每天新运来的纪念品数量是前四个摊点每天新增总量的.第3天结束营业时,第四、五号摊点的纪念品恰好售完并撤走摊点;第4天结束营业时,第一、二、三、六号摊点的所有纪念品均售完并撤走.若第四号和第六号摊点平均每天售出的纪念品数量相等,则A、B两社区售出纪念品的总数量之比为 .
【分析】设每个摊点原有纪念品x件,第一、二、三、四号摊点每天新运来y件纪念品,则第五号摊点每天新运来4×y件纪念品,第六号摊点每天新运来4×y件纪念品,根据第四号和第六号摊点平均每天售出的纪念品数量相等,即可找出关于x,y的二元一次方程,化简后可得出x=2y,用含y的代数式分别表示出两社区售出纪念品的总数量,二者相除后即可得出A、B两社区售出纪念品的总数量之比为.
解:设每个摊点原有纪念品x件,第一、二、三、四号摊点每天新运来y件纪念品,则第五号摊点每天新运来4×y件纪念品,第六号摊点每天新运来4×y件纪念品,
依题意得:=,
化简得:x=2y,
∴A社区售出纪念品的总数量为4(x+4y)=24y(件),B社区售出纪念品的总数量为(x+3y)+(x+3×4×y)+(x+4×4×y)=15y(件),
∴A、B两社区售出纪念品的总数量之比为=.
故答案为:.
三、解答题:(本大题3个小题,19题8分,20、21题各10分,共28分)解答时每小题必须给出演算过程或推理步骤.
19.计算:
(1)|﹣1|﹣(π﹣2)0+(﹣)﹣2;
(2)(6﹣)÷.
【分析】(1)先利用零指数幂、负整数指数幂的运意义和绝对值的意义计算;
(2)根据利用二次根式的除法法则计算.
解:(1)原式=﹣1﹣1+4
=+2;
(2)原式=6﹣
=6×﹣
=2﹣.
20.解方程组:
(1);
(2).
【分析】(1)用①+②消去未知数y,即可求出未知数x,再把x的值代入其中一个方程求出y的值即可;
(2)原方程组可化为,用①×3+②可消去未知数y,进而求出x的值,再把x的值代入其中一个方程求出y的值即可.
解:(1),
①+②,得3x=6,
解得x=2,
把x=2代入②,得y=1,
故原方程组的解为;
(2)原方程组可化为,
①×3+②,得7x=28,
解得x=4,
把x=4代入①,得y=4,
故原方程组的解为.
21.解不等式(组):
(1)4(x﹣2)+7<3;
(2).
【分析】(1)不等式去括号,移项,合并同类项,把x系数化为1,即可求出解集;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解:(1)去括号得:4x﹣8+7<3,
移项得:4x<3+8﹣7,
合并得:4x<4,
解得:x<1;
(2),
由①得:x>﹣2,
由②得:x<﹣,
则不等式组的解集为﹣2<x<﹣.
四、解答题:(本大题5个小题,每小题10分,共50分)解答时每小题必须给出必要的演算过程或步骤.
22.某中学团委在第十个“全国交通安全日”组织开展交通安全知识竞赛,现从七、八年级中各随机抽取20名学生的竞赛成绩(百分制)进行整理和分析(成绩均为整数,成绩得分用x表示),共分成五个等级.A:0≤x≤60,B:60<x≤70,C:70<x≤80,D:80<x≤90,E:90<x≤100,下面给出了部分信息:
七年级抽取的20名学生的竞赛成绩在D等级中的数据分别是:83,85,85,85,85,90.
八年级抽取的20名学生的竞赛成绩在D等级中的数据分别是:83,84,85,85,85,90,90.
七、八年级抽取的学生竞赛成绩统计表
根据以上信息,解答下列问题:
(1)请补全条形统计图,并直接写出a、b的值;
(2)根据以上数据分析,你认为哪个年级的竞赛成绩更好,并说明理由(写出一条理由即可);
(3)已知该校七、八年级共有1200名学生参与了知识竞赛,请估计两个年级竞赛成绩优秀的学生共有多少人(其中成绩大于90的为优秀)?
【分析】(1)根据总人数是20人,可得C组的人数为:20﹣1﹣2﹣7﹣6=4(人),从而补全条形统计图,然后根据中位数和众数的定义求出a、b的值;
(2)根据表格中的数据,可以得到哪个年级的成绩好一些,并说明理由;
(3)用样本估计总体可得结果.
解:(1)年级抽取的20名学生的竞赛成绩在C等级人数为:20﹣1﹣2﹣7﹣6=4(人),
补全条形统计图如下:
因为七年级取的20名学生的竞赛成绩从小到大排在中间的两个数分别是83,85,所以a=×(83+85)=84;
因为八年级抽取的20名学生的竞赛成绩中85出现的次数最多,所以b=85;
(2)八年级的成绩好一些,理由:八年级的平均成绩好于七年级,中位数也大于七年级,故八年级的成绩好一些;
(3)1200×(20%+)÷2=300(人),
答:估计两个年级竞赛成绩优秀的学生共有300人.
23.如图所示,每个小方格都是边长为1个单位长度的正方形,Rt△ABC的顶点均在格点上,∠ACB=90°,在建立平面直角坐标系后,解答下列问题.
(1)点A坐标为 (1,4) ,点B坐标为 (3,1) ;
(2)将△ABC向左平移4个单位,再向下平移5个单位得到△A1B1C1,若△ABC内部任意一点P(a,b)随△ABC一起平移,则点P平移后的对应点P1坐标为 (a﹣4,b﹣5) ,PP1的长为 ;
(3)将△ABC绕点C逆时针旋转90°得到△A2B2C2,在图中画出旋转后的△A2B2C2,并求出边CB在旋转过程中所扫过的面积(结果保留π).
【分析】(1)根据坐标系即可得点A坐标,点B坐标;
(2)根据平移的性质将△ABC向左平移4个单位,再向下平移5个单位得到△A1B1C1,可得点P平移后的对应点P1坐标,然后根据勾股定理即可求出PP1的长;
(3)根据旋转的性质即可将△ABC绕点C逆时针旋转90°得到△A2B2C2,根据扇形面积公式即可求出边CB在旋转过程中所扫过的面积.
解:(1)点A坐标为(1,4),点B坐标为(3,1);
故答案为:(1,4),(3,1);
(2)根据平移可得点P平移后的对应点P1坐标为(a﹣4,a﹣5),
∴PP1的长为=,
故答案为:(a﹣4,a﹣5),;
(3)如图,△A2B2C2即为所求;
边CB在旋转过程中所扫过的面积==π.
24.如图所示,平面直角坐标系中,直线l1:y=﹣2x+3与直线l2:y=x+1相交于点A,直线l2与x轴相交于点B.过直线l2上的一点P(a,﹣1)作y轴的垂线,交直线l1于点C,连接BC.
(1)求点A的坐标;
(2)求△ABC的面积;
(3)将直线l1向下平移4个单位长度得到直线l3,设直线l3与y轴相交于点D,则直线l2上是否存在一点Q,使得△DPQ是以DP为腰的等腰三角形?若存在,请直接写出Q的坐标,若不存在,请说明理由.
【分析】(1)联立方程组可求解;
(2)分别求出点B,点C坐标,由三角形的面积公式可求解;
(3)先求出点D坐标,由等腰三角形的性质和两点之间的距离公式可求解.
解:(1)由题意可得:,
解得:,
∴点A(,);
(2)∵直线l2与x轴相交于点B,
∴点B(﹣1,0),
∵点P(a,﹣1)在直线l2上,
∴﹣1=a+1,
∴a=﹣2,
∴点P(﹣2,﹣1),
∴点C的纵坐标为﹣1,
∴﹣1=﹣2x+3,
∴x=2,
∴点C(2,﹣1),
如图,设直线l1与x轴相交于点H,
∴0=﹣2x+3,
∴x=,
∴点H(,0),
∴BH=,
∴△ABC的面积=××(+1)=;
(3)存在,理由如下:
∵将直线l1向下平移4个单位长度得到直线l3,
∴直线l3,的解析式为:y=﹣2x﹣1,
∴点D(0,﹣1),
如图,
∵点P(﹣2,﹣1),点D(0,﹣1),
∴PD⊥y轴,PD=2,
设点Q(a,a+1),
∵△DPQ是以DP为腰的等腰三角形,
∴PQ=PD=2或PD=QD=2,
当PQ=PD=2时,则(﹣2﹣a)2+(﹣1﹣a﹣1)2=4,
∴a=±﹣2,
∴点Q(﹣2,﹣1)或(﹣﹣2,﹣﹣1);
当PD=QD=2时,则(a﹣0)2+(﹣1﹣a﹣1)2=4,
∴a=0或﹣2(不合题意舍去),
∴点Q(0,1),
综上所述:点Q坐标为:(﹣2,﹣1)或(﹣﹣2,﹣﹣1)或(0,1).
25.“红缬退风花著子,绿针浮水稻抽秧”这是宋朝诗人姚孝锡所作.诗中咏诵的“水稻”是我国种植的重要经济作物.某村在政府的扶持下建起了水稻种植基地,准备种植甲,乙两种水稻,若种植20亩甲种水稻和30亩乙种水稻,共需投入22万元;若种植30亩甲种水稻和20亩乙种水稻,共需投入23万元.
(1)种植甲,乙两种水稻,每亩各需投入多少万元?
(2)经测算,种植甲种水稻每亩可获利a(a>0且a为常数)万元,种植乙种水稻每亩可获利0.8万元,村里投入50万元用来种植这两种水稻,若要求甲种水稻的种植面积不能少于乙种水稻种植面积的倍,且不能多于乙种水稻种植面积的倍.设种植乙种水稻m亩,该村种植两种水稻共获利W万元,请求出W关于m的函数表达式,并求出最大获利(用含a的代数式表示).
【分析】(1)根据题意列二元一次方程组即可得到答案;
(2)由题意甲种水稻的种植面积为=(100﹣0.8m)亩,根据甲种水稻的种植面积不能少于乙种水稻种植面积的倍,且不能多于乙种水稻种植面积的倍,可得25≤m≤50,而W=(100﹣0.8m) a+0.8m=(0.8﹣0.8a)m+100a,当0<a<1时,m=50时,最大获利W为(0.8﹣0.8a)×50+100a=(60a+40)万元,当a=1时,W=100a(万元),当a>1时,m=25时,最大获利W为(0.8﹣0.8a)×25+100a=(80a+20)万元.
解:(1)设甲种水稻每亩需投入x万元,乙种水稻每亩需投入y万元,
根据题意得,
解得,
答:甲种水稻每亩需投入0.5万元,乙种水稻每亩需投入0.4万元;
(2)由题意甲种水稻的种植面积为=(100﹣0.8m)亩,
∵甲种水稻的种植面积不能少于乙种水稻种植面积的倍,且不能多于乙种水稻种植面积的倍,
∴m≤100﹣0.8m≤m,
解得25≤m≤50,
∵种植甲种水稻每亩可获利a(a>0且a为常数)万元,种植乙种水稻每亩可获利0.8万元,
∴W=(100﹣0.8m) a+0.8m=(0.8﹣0.8a)m+100a,
当0<a<1时,0.8﹣0.8a>0,W随m的增大而增大,
∴m=50时,最大获利W为(0.8﹣0.8a)×50+100a=(60a+40)万元,
当a=1时,W=100a(万元),
当a>1时,0.8﹣0.8a<0,W随m的增大而减小,
∴m=25时,最大获利W为(0.8﹣0.8a)×25+100a=(80a+20)万元,
综上所述,当0<a<1时,最大获利W为(60a+40)万元,当a=1时,W=100a万元,当a>1时,最大获利W为(80a+20)万元.
26.在平行四边形ABCD中,连接BD,若BD⊥CD,点E为边AD上一点,连接CE.
(1)如图1,点G在BD上,且DG=DC,连接CG,过G作GH⊥CE于点H,连接DH并延长交AB于点M,若HG=BM,求证:BM+DH=DB;
(2)如图2,∠ABC=120°,AB=,点N在BC边上,BC=4CN,若CE是∠DCB的角平分线,线段PQ(点P在点Q的左侧)在线段CE上运动,PQ=,连接BP、NQ,请直接写出BP+PQ+QN的最小值.
【分析】(1)如图1,过点D作DF⊥DM交CE于点F,设CE与BD交于点K,先证明△DCF≌△DGH(ASA),进而证得△DFH是等腰直角三角形,得出FH=DH,再证明△DMB≌△CGH(AAS),推出CF=BM,即可证得结论;
(2)如图2,在CD上截取CG=CN,连接GQ,过点B作BF∥CE,使BF=PQ=,连接DF交CE于点T,连接QF,过点F作FM⊥BD于点M,过点G作GH⊥DF于点H,应用平行四边形的性质和含30°直角三角形三边关系可得:BC=2CD=2,利用勾股定理可得BD=,再利用含30°直角三角形三边关系可得:BM=BF=,FM=BM=,进而可得DM=,求得:FG=,再证四边形BPQF是平行四边形,得出BP=FQ,再证明△CNQ≌△CGQ(SAS),得出QN=QG,根据FQ+QG≥FG,可得出:当点Q在线段FG上时,FQ+QG的最小值为FG,即BP+QN的最小值为FG,即可求得BP+PQ+QN的最小值.
解:(1)如图1,过点D作DF⊥DM交CE于点F,设CE与BD交于点K,
∵BD⊥CD,DF⊥DM,GH⊥CE,
∴∠CDG=∠FDH=∠CHG=90°,
∴∠CDF=∠GDH,
∵∠DGH+∠HKG=∠DCF+∠DKC=90°,∠HKG=∠DKC,
∴∠DCF=∠DGH,
在△DCF和△DGH中,
,
∴△DCF≌△DGH(ASA),
∴DF=DH,CF=GH,
∵∠FDH=90°,
∴△DFH是等腰直角三角形,
∴∠DFH=∠DHF=45°,FH=DH,
∵DC=DG,∠CDG=90°,
∴∠CGD=DCG=45°,
∴∠CGD=∠DHF,
∵∠CGD+∠GCH+∠CKG=∠DHF+∠BDM+∠DKH=180°,∠CKG=∠DKH,
∴∠GCH=∠BDM,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DBM=∠CDG=90°=∠CHG,
在△DMB和△CGH中,
,
∴△DMB≌△CGH(AAS),
∴DB=CH,
∵CF=GH,BM=GH,
∴CF=BM,
∵CF+FH=CH,
∴BM+DH=DB;
(2)如图2,在CD上截取CG=CN,连接GQ,过点B作BF∥CE,使BF=PQ=,
连接DF交CE于点T,连接QF,过点F作FM⊥BD于点M,过点G作GH⊥DF于点H,
∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=,
∵∠ABC=120°,
∴∠BCD=180°﹣120°=60°,
∵BD⊥CD,CD=,
∴∠CBD=90°﹣60°=30°,
∴BC=2CD=2,
∴BD===,
∵CE平分∠DCB,
∴∠BCE=∠DCE=∠DCB=×60°=30°,
∵BF∥CE,
∴∠CBF=∠BCE=30°,
∴∠DBF=∠CBF+∠CBD=30°+30°=60°,
∵FM⊥BD,BF=,
∴BM=BF=×=,FM=BM=×=,
∴DM=BD﹣BM=﹣=,
∴DF===,
∵DF2+BF2=()2+()2=15,
∴DF2+BF2=BD2,
∴BF⊥DF,
∵BF∥CE,
∴CE⊥DF,
∵∠DCE=30°,
∴∠CDF=90°﹣30°=60°,
∵BC=2,BC=4CN,
∴CN=×2=,
∴CG=CN=,
∴DG=CD﹣CG=﹣=,
∵GH⊥DF,∠CDF=60°,
∴DH=DG=×=,GH=DH=×=,
∴FH=DF﹣DH=﹣=,
∴FG===,
∵BF∥CE,BF=PQ,
∴四边形BPQF是平行四边形,
∴BP=FQ,
在△CNQ和△CGQ中,
,
∴△CNQ≌△CGQ(SAS),
∴QN=QG,
∵FQ+QG≥FG,
∴当点Q在线段FG上时,FQ+QG的最小值为FG,
∴BP+QN的最小值为FG,
∵PQ=,FG=,
∴BP+PQ+QN的最小值为FG+PQ=+=,
故BP+PQ+QN的最小值为.
一、选择题(本大题10个小题,每小题4分,共40分).
1.下列各数中,是无理数的是( )
A.2 B. C. D.
2.下列图形中,是中心对称图形的是( )
A. B. C. D.
3.计算(3a3)2的结果是( )
A.9a6 B.9a5 C.6a6 D.6a5
4.若x>y,则下列不等式一定成立的是( )
A.﹣x>﹣y B.2x<2y C. D.x+4>y+4
5.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AB=CD B.AB=CD,AD=BC
C.AB∥CD,∠B=∠D D.AB∥CD,AD=BC
6.如图所示,在平行四边形ABCD中,已知AB=8,AD=3,AE平分∠BAD交DC于点E,则CE的长为( )
A.3 B.4 C.5 D.8
7.估计×﹣4的值应该在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
8.如图所示,在平面直角坐标系中,等腰Rt△ABC的直角顶点C在x轴上,点A在y轴上,若点B坐标为(6,1),则点A坐标为( )
A.(4,0) B.(5,0) C.(0,4) D.(0,5)
9.如图所示,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′B′C′,其中点A,C的对应点分别为点A′,C′,当点C′落在AB的延长线上时,在A'B上取一点D,使得BD=3,则CD的长为( )
A.3 B.3.6 C.4 D.4.8
10.如图所示,在长方形ABCD中,AB=2,在线段BC上取一点E,连接AE、ED,将△ABE沿AE翻折,点B落在点B'处,线段EB'交AD于点F.将△ECD沿DE翻折,点C的对应点C'恰好落在线段EB'上,且点C'为EB'的中点,则线段EF的长为( )
A.3 B. C.4 D.
二、填空题:(本大题共8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卷中对应的横线上.
11.在平面直角坐标系中,若点P(﹣1,m﹣5)在x轴上,则m的值为 .
12.已知A(x1,y1)、B(x2,y2)是一次函数y=﹣5x+7上两点,若x1>x2,则y1 y2.
13.若实数x,y满足y=4+,则的值是 .
14.若直线l向右平移2个单位长度后对应直线的解析式为y=2x+3,则直线l的解析式为 .
15.若关于x的不等式﹣ax>b(a,b≠0)的解集为x<﹣,则的值为 .
16.若整数a使关于x的一次函数y=﹣x+a﹣2不经过第三象限,且使关于y的不等式组有且仅有4个整数解,则所有满足条件的整数a的值之和为 .
17.如图,将平行四边形ABCD绕点D顺时针旋转150°得到四边形EFGD,这时点C,E,G恰好在同一直线上,延长AD交CG于点H.若AD=2,∠A=75°,则HG= .
18.为迎接北京冬奥会,在A、B两个社区共设置六个摊点售卖冬奥纪念品,其中第一、二、三号摊点在A社区,第四、五、六号摊点在B社区,每个摊点原有纪念品一样多.第一、二、三、四号摊点每天新运来相等数量的纪念品,第五号摊点每天新运来的纪念品数量是前四个摊点每天新增总量的,第六号摊点每天新运来的纪念品数量是前四个摊点每天新增总量的.第3天结束营业时,第四、五号摊点的纪念品恰好售完并撤走摊点;第4天结束营业时,第一、二、三、六号摊点的所有纪念品均售完并撤走.若第四号和第六号摊点平均每天售出的纪念品数量相等,则A、B两社区售出纪念品的总数量之比为 .
三、解答题:(本大题3个小题,19题8分,20、21题各10分,共28分)解答时每小题必须给出演算过程或推理步骤.
19.计算:
(1)|﹣1|﹣(π﹣2)0+(﹣)﹣2;
(2)(6﹣)÷.
20.解方程组:
(1);
(2).
21.解不等式(组):
(1)4(x﹣2)+7<3;
(2).
四、解答题:(本大题5个小题,每小题10分,共50分)解答时每小题必须给出必要的演算过程或步骤.
22.某中学团委在第十个“全国交通安全日”组织开展交通安全知识竞赛,现从七、八年级中各随机抽取20名学生的竞赛成绩(百分制)进行整理和分析(成绩均为整数,成绩得分用x表示),共分成五个等级.A:0≤x≤60,B:60<x≤70,C:70<x≤80,D:80<x≤90,E:90<x≤100,下面给出了部分信息:
七年级抽取的20名学生的竞赛成绩在D等级中的数据分别是:83,85,85,85,85,90.
八年级抽取的20名学生的竞赛成绩在D等级中的数据分别是:83,84,85,85,85,90,90.
七、八年级抽取的学生竞赛成绩统计表
根据以上信息,解答下列问题:
(1)请补全条形统计图,并直接写出a、b的值;
(2)根据以上数据分析,你认为哪个年级的竞赛成绩更好,并说明理由(写出一条理由即可);
(3)已知该校七、八年级共有1200名学生参与了知识竞赛,请估计两个年级竞赛成绩优秀的学生共有多少人(其中成绩大于90的为优秀)?
23.如图所示,每个小方格都是边长为1个单位长度的正方形,Rt△ABC的顶点均在格点上,∠ACB=90°,在建立平面直角坐标系后,解答下列问题.
(1)点A坐标为 ,点B坐标为 ;
(2)将△ABC向左平移4个单位,再向下平移5个单位得到△A1B1C1,若△ABC内部任意一点P(a,b)随△ABC一起平移,则点P平移后的对应点P1坐标为 ,PP1的长为 ;
(3)将△ABC绕点C逆时针旋转90°得到△A2B2C2,在图中画出旋转后的△A2B2C2,并求出边CB在旋转过程中所扫过的面积(结果保留π).
24.如图所示,平面直角坐标系中,直线l1:y=﹣2x+3与直线l2:y=x+1相交于点A,直线l2与x轴相交于点B.过直线l2上的一点P(a,﹣1)作y轴的垂线,交直线l1于点C,连接BC.
(1)求点A的坐标;
(2)求△ABC的面积;
(3)将直线l1向下平移4个单位长度得到直线l3,设直线l3与y轴相交于点D,则直线l2上是否存在一点Q,使得△DPQ是以DP为腰的等腰三角形?若存在,请直接写出Q的坐标,若不存在,请说明理由.
25.“红缬退风花著子,绿针浮水稻抽秧”这是宋朝诗人姚孝锡所作.诗中咏诵的“水稻”是我国种植的重要经济作物.某村在政府的扶持下建起了水稻种植基地,准备种植甲,乙两种水稻,若种植20亩甲种水稻和30亩乙种水稻,共需投入22万元;若种植30亩甲种水稻和20亩乙种水稻,共需投入23万元.
(1)种植甲,乙两种水稻,每亩各需投入多少万元?
(2)经测算,种植甲种水稻每亩可获利a(a>0且a为常数)万元,种植乙种水稻每亩可获利0.8万元,村里投入50万元用来种植这两种水稻,若要求甲种水稻的种植面积不能少于乙种水稻种植面积的倍,且不能多于乙种水稻种植面积的倍.设种植乙种水稻m亩,该村种植两种水稻共获利W万元,请求出W关于m的函数表达式,并求出最大获利(用含a的代数式表示).
26.在平行四边形ABCD中,连接BD,若BD⊥CD,点E为边AD上一点,连接CE.
(1)如图1,点G在BD上,且DG=DC,连接CG,过G作GH⊥CE于点H,连接DH并延长交AB于点M,若HG=BM,求证:BM+DH=DB;
(2)如图2,∠ABC=120°,AB=,点N在BC边上,BC=4CN,若CE是∠DCB的角平分线,线段PQ(点P在点Q的左侧)在线段CE上运动,PQ=,连接BP、NQ,请直接写出BP+PQ+QN的最小值.
参考答案
一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将正确答案填写在答题卷上对应的位置.
1.下列各数中,是无理数的是( )
A.2 B. C. D.
【分析】根据无理数是无限不循环小数,可得答案.
解:A、2是整数,属于有理数,故此选项不符合题意;
B、﹣是分数,属于有理数,故此选项不符合题意;
C、是无理数,故此选项符合题意;
D、是无限循环小数,属于有理数,故此选项不符合题意.
故选:C.
2.下列图形中,是中心对称图形的是( )
A. B. C. D.
【分析】根据中心对称图形的概念求解判断即可.
解:A.不是中心对称图形,故此选项不符合题意;
B.不是中心对称图形,故此选项不符合题意;
C.是中心对称图形,故此选项符合题意;
D.不是中心对称图形,故此选项不符合题意.
故选:C.
3.计算(3a3)2的结果是( )
A.9a6 B.9a5 C.6a6 D.6a5
【分析】根据幂的乘方与积的乘方法则进行计算即可得出结果.
解:(3a3)2=9(a3)2=9a6,
故选:A.
4.若x>y,则下列不等式一定成立的是( )
A.﹣x>﹣y B.2x<2y C. D.x+4>y+4
【分析】根据不等式的性质判断即可.
解:A.因为x>y,所以﹣x<﹣y,故A不符合题意;
B.因为x>y,所以2x>2y,故B不符合题意;
C.因为x>y,所以>,故C不符合题意;
D.因为x>y,所以x+4>y+4,故D符合题意;
故选:D.
5.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AB=CD B.AB=CD,AD=BC
C.AB∥CD,∠B=∠D D.AB∥CD,AD=BC
【分析】根据平行四边形的判定定理分别进行分析即可.
解:A、∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,故此选项不合题意;
B、∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,故此选项不合题意;
C、∵AB∥CD,∠B=∠D,∴四边形ABCD是平行四边形,故此选项不合题意;
D、∵AB∥CD,AD=BC,不能得出四边形ABCD是平行四边形,故此选项符合题意;
故选:D.
6.如图所示,在平行四边形ABCD中,已知AB=8,AD=3,AE平分∠BAD交DC于点E,则CE的长为( )
A.3 B.4 C.5 D.8
【分析】由平行四边形的性质得出BC=AD=5,AD∥BC,得出∠DAE=∠BEA,证出∠BEA=∠BAE,得出BE=AB,即可得出CE的长.
解:∵四边形ABCD是平行四边形,
∴CD=AB=8,AB∥DC,
∴∠BAE=∠DEA,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠DEA=∠DAE,
∴DE=AD=3,
∴CE=DC﹣CE=8﹣3=5;
故选:C.
7.估计×﹣4的值应该在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
【分析】先进行二次根式的混合运算,然后再估算出的值即可解答.
解:×﹣4
=5﹣4
=,
∵4<6<9,
∴2<<3,
∴估计×﹣4的值应该在:2和3之间,
故选:B.
8.如图所示,在平面直角坐标系中,等腰Rt△ABC的直角顶点C在x轴上,点A在y轴上,若点B坐标为(6,1),则点A坐标为( )
A.(4,0) B.(5,0) C.(0,4) D.(0,5)
【分析】作BD⊥x轴于D,证明△ACO≌△CBD(AAS),得OC=BD=1,CD=OA=5,从而解决问题.
解:作BD⊥x轴于D,
∵B(6,1),
∴BD=1,OD=6,
∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴∠ACO+∠BCD=90°,
∵∠ACO+∠OAC=90°,
∴∠BCD=∠OAC,
∵∠AOC=∠BDO,
∴△ACO≌△CBD(AAS),
∴OC=BD=1,CD=OA=5,
∴A(0,5),
故选:D.
9.如图所示,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′B′C′,其中点A,C的对应点分别为点A′,C′,当点C′落在AB的延长线上时,在A'B上取一点D,使得BD=3,则CD的长为( )
A.3 B.3.6 C.4 D.4.8
【分析】过B作BE⊥CD于E,根据△ABC绕点B顺时针旋转得到△A′BC′,可得∠ABC=∠A'BC',而BC=BD=3,可得∠BCD=∠BDC,由∠ABC+∠A'BC'+∠CBD=180°=∠BCD+∠BDC+∠CBD,即得∠ABC=∠BCD,故△ACB∽△BEC,可得=,CE=1.8,从而CD=2CE=3.6.
解:过B作BE⊥CD于E,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴∠ABC=∠A'BC',
∵BC=BD=3,
∴∠BCD=∠BDC,
∵∠ABC+∠A'BC'+∠CBD=180°=∠BCD+∠BDC+∠CBD,
∴∠ABC=∠BCD,
∵∠ACB=∠CEB=90°,
∴△ACB∽△BEC,
∴=,即=,
∴CE=1.8,
∵BC=BD,BE⊥CD,
∴CD=2CE=3.6,
故选:B.
10.如图所示,在长方形ABCD中,AB=2,在线段BC上取一点E,连接AE、ED,将△ABE沿AE翻折,点B落在点B'处,线段EB'交AD于点F.将△ECD沿DE翻折,点C的对应点C'恰好落在线段EB'上,且点C'为EB'的中点,则线段EF的长为( )
A.3 B. C.4 D.
【分析】由折叠的性质可得AB=AB'=CD=C'D=2,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,由中点性质可得B'E=2C'E,可得BC=AD=3EC,由勾股定理可求可求CE的长,由“AAS”可证△AB'F≌△DC'F,可得C'F=B'F=1,即可求解.
解:∵四边形ABCD是矩形,
∴AB=CD=1,AD=BC,∠B=∠C=90°
由折叠的性质可得:AB=AB'=CD=C'D=2,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,
∵点C'恰好为EB'的中点,
∴B'E=2C'E,
∴BE=2CE,
∴BC=AD=3EC,
∵AE2=AB2+BE2,DE2=DC2+CE2,AD2=AE2+DE2,
∴8+4CE2+8+CE2=9CE2,
∴CE=2,
∴B'E=BE=4,BC=AD=6,C'E=2,
∴B'C'=2,
∵∠B'=∠DC'F=90°,∠AFB'=∠DFC',AB'=C'D,
∴△AB'F≌△DC'F(AAS),
∴C'F=B'F=1,
∴EF=C'E+C'F=3,
故选:A.
二、填空题:(本大题共8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卷中对应的横线上.
11.在平面直角坐标系中,若点P(﹣1,m﹣5)在x轴上,则m的值为 5 .
【分析】根据x轴上点的纵坐标为0列方程求解即可.
解:∵点P(﹣1,m﹣5)在x轴上,
∴m﹣5=0,
解得m=5.
故答案为:5.
12.已知A(x1,y1)、B(x2,y2)是一次函数y=﹣5x+7上两点,若x1>x2,则y1 < y2.
【分析】由k=﹣2<0根据一次函数的性质可得出结论.
解:∵一次函数y=﹣5x+7中k=﹣5<0,
∴该一次函数y随x的增大而减小,
∵x1>x2,
∴y1<y2.
故答案为:<.
13.若实数x,y满足y=4+,则的值是 3 .
【分析】根据二次根式有意义的条件可得:,解出x的值,进而可得y的值,然后可得答案.
解:由题意得:,
解得:x=5,
则y=4,
===3,
故答案为:3.
14.若直线l向右平移2个单位长度后对应直线的解析式为y=2x+3,则直线l的解析式为 y=2x+7 .
【分析】直接根据“左加右减”的原则进行解答即可.
解:由“左加右减”的原则可知:把直线y=2x+3向左平移2个单位长度后,其直线l的解析式为y=2(x+2)+3,即y=2x+7.
故答案为:y=2x+7.
15.若关于x的不等式﹣ax>b(a,b≠0)的解集为x<﹣,则的值为 .
【分析】根据题意可得x<﹣,从而求出=,然后利用设k法进行计算即可解答.
解:由题意得:
x<﹣,
∵不等式解集为x<﹣,
∴=,
∴设b=2k,a=3k,
∴===,
故答案为:.
16.若整数a使关于x的一次函数y=﹣x+a﹣2不经过第三象限,且使关于y的不等式组有且仅有4个整数解,则所有满足条件的整数a的值之和为 5 .
【分析】由该一次函数不经过第三象限,可得a﹣2≥0,解得a≥2;解不等式组,并根据不等式有4个整数解,进而得出a的取值范围.
解:∵关于x的一次函数y=﹣x+a﹣2不经过第三象限,
∴a﹣2≥0,解得a≥2,
解关于y的不等式组,
解①得y≤2,解②得y>,
∵关于y的不等式组有且仅有4个整数解,
∴﹣2≤<﹣1,
解得1<a≤,
∴2≤a≤,
∵a为整数,
∴满足条件的a的值为2,3,
∴2+3=5,
故答案为:5.
17.如图,将平行四边形ABCD绕点D顺时针旋转150°得到四边形EFGD,这时点C,E,G恰好在同一直线上,延长AD交CG于点H.若AD=2,∠A=75°,则HG= 3+2 .
【分析】证明△CDG是顶角为150°的等腰三角形,再证明DH⊥CG,由直角三角形的性质求出DH,进而解决问题.
解:在CG上取一点K,使DK=GK,如图:
由题意:∠ADE=150°,AD=DE=2,
∴∠EDH=30°,
∵AB∥CD,
∴∠CDH=∠A=75°,
∵∠CDG=150°,DC=DG,
∴∠DGC=∠DCG=15°,∠CDH=∠GDH=75°,
∴DH⊥CG,
∴EH=DE=1,DH=EH=,
∵DK=GK,
∴∠KDG=∠KGD=15°,
∴∠DKH=15°+15°=30°,
∴KG=DK=2DH=2,HK=DH=3,
∴HG=HK+KG=3+2,
故答案为:3+2.
18.为迎接北京冬奥会,在A、B两个社区共设置六个摊点售卖冬奥纪念品,其中第一、二、三号摊点在A社区,第四、五、六号摊点在B社区,每个摊点原有纪念品一样多.第一、二、三、四号摊点每天新运来相等数量的纪念品,第五号摊点每天新运来的纪念品数量是前四个摊点每天新增总量的,第六号摊点每天新运来的纪念品数量是前四个摊点每天新增总量的.第3天结束营业时,第四、五号摊点的纪念品恰好售完并撤走摊点;第4天结束营业时,第一、二、三、六号摊点的所有纪念品均售完并撤走.若第四号和第六号摊点平均每天售出的纪念品数量相等,则A、B两社区售出纪念品的总数量之比为 .
【分析】设每个摊点原有纪念品x件,第一、二、三、四号摊点每天新运来y件纪念品,则第五号摊点每天新运来4×y件纪念品,第六号摊点每天新运来4×y件纪念品,根据第四号和第六号摊点平均每天售出的纪念品数量相等,即可找出关于x,y的二元一次方程,化简后可得出x=2y,用含y的代数式分别表示出两社区售出纪念品的总数量,二者相除后即可得出A、B两社区售出纪念品的总数量之比为.
解:设每个摊点原有纪念品x件,第一、二、三、四号摊点每天新运来y件纪念品,则第五号摊点每天新运来4×y件纪念品,第六号摊点每天新运来4×y件纪念品,
依题意得:=,
化简得:x=2y,
∴A社区售出纪念品的总数量为4(x+4y)=24y(件),B社区售出纪念品的总数量为(x+3y)+(x+3×4×y)+(x+4×4×y)=15y(件),
∴A、B两社区售出纪念品的总数量之比为=.
故答案为:.
三、解答题:(本大题3个小题,19题8分,20、21题各10分,共28分)解答时每小题必须给出演算过程或推理步骤.
19.计算:
(1)|﹣1|﹣(π﹣2)0+(﹣)﹣2;
(2)(6﹣)÷.
【分析】(1)先利用零指数幂、负整数指数幂的运意义和绝对值的意义计算;
(2)根据利用二次根式的除法法则计算.
解:(1)原式=﹣1﹣1+4
=+2;
(2)原式=6﹣
=6×﹣
=2﹣.
20.解方程组:
(1);
(2).
【分析】(1)用①+②消去未知数y,即可求出未知数x,再把x的值代入其中一个方程求出y的值即可;
(2)原方程组可化为,用①×3+②可消去未知数y,进而求出x的值,再把x的值代入其中一个方程求出y的值即可.
解:(1),
①+②,得3x=6,
解得x=2,
把x=2代入②,得y=1,
故原方程组的解为;
(2)原方程组可化为,
①×3+②,得7x=28,
解得x=4,
把x=4代入①,得y=4,
故原方程组的解为.
21.解不等式(组):
(1)4(x﹣2)+7<3;
(2).
【分析】(1)不等式去括号,移项,合并同类项,把x系数化为1,即可求出解集;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解:(1)去括号得:4x﹣8+7<3,
移项得:4x<3+8﹣7,
合并得:4x<4,
解得:x<1;
(2),
由①得:x>﹣2,
由②得:x<﹣,
则不等式组的解集为﹣2<x<﹣.
四、解答题:(本大题5个小题,每小题10分,共50分)解答时每小题必须给出必要的演算过程或步骤.
22.某中学团委在第十个“全国交通安全日”组织开展交通安全知识竞赛,现从七、八年级中各随机抽取20名学生的竞赛成绩(百分制)进行整理和分析(成绩均为整数,成绩得分用x表示),共分成五个等级.A:0≤x≤60,B:60<x≤70,C:70<x≤80,D:80<x≤90,E:90<x≤100,下面给出了部分信息:
七年级抽取的20名学生的竞赛成绩在D等级中的数据分别是:83,85,85,85,85,90.
八年级抽取的20名学生的竞赛成绩在D等级中的数据分别是:83,84,85,85,85,90,90.
七、八年级抽取的学生竞赛成绩统计表
根据以上信息,解答下列问题:
(1)请补全条形统计图,并直接写出a、b的值;
(2)根据以上数据分析,你认为哪个年级的竞赛成绩更好,并说明理由(写出一条理由即可);
(3)已知该校七、八年级共有1200名学生参与了知识竞赛,请估计两个年级竞赛成绩优秀的学生共有多少人(其中成绩大于90的为优秀)?
【分析】(1)根据总人数是20人,可得C组的人数为:20﹣1﹣2﹣7﹣6=4(人),从而补全条形统计图,然后根据中位数和众数的定义求出a、b的值;
(2)根据表格中的数据,可以得到哪个年级的成绩好一些,并说明理由;
(3)用样本估计总体可得结果.
解:(1)年级抽取的20名学生的竞赛成绩在C等级人数为:20﹣1﹣2﹣7﹣6=4(人),
补全条形统计图如下:
因为七年级取的20名学生的竞赛成绩从小到大排在中间的两个数分别是83,85,所以a=×(83+85)=84;
因为八年级抽取的20名学生的竞赛成绩中85出现的次数最多,所以b=85;
(2)八年级的成绩好一些,理由:八年级的平均成绩好于七年级,中位数也大于七年级,故八年级的成绩好一些;
(3)1200×(20%+)÷2=300(人),
答:估计两个年级竞赛成绩优秀的学生共有300人.
23.如图所示,每个小方格都是边长为1个单位长度的正方形,Rt△ABC的顶点均在格点上,∠ACB=90°,在建立平面直角坐标系后,解答下列问题.
(1)点A坐标为 (1,4) ,点B坐标为 (3,1) ;
(2)将△ABC向左平移4个单位,再向下平移5个单位得到△A1B1C1,若△ABC内部任意一点P(a,b)随△ABC一起平移,则点P平移后的对应点P1坐标为 (a﹣4,b﹣5) ,PP1的长为 ;
(3)将△ABC绕点C逆时针旋转90°得到△A2B2C2,在图中画出旋转后的△A2B2C2,并求出边CB在旋转过程中所扫过的面积(结果保留π).
【分析】(1)根据坐标系即可得点A坐标,点B坐标;
(2)根据平移的性质将△ABC向左平移4个单位,再向下平移5个单位得到△A1B1C1,可得点P平移后的对应点P1坐标,然后根据勾股定理即可求出PP1的长;
(3)根据旋转的性质即可将△ABC绕点C逆时针旋转90°得到△A2B2C2,根据扇形面积公式即可求出边CB在旋转过程中所扫过的面积.
解:(1)点A坐标为(1,4),点B坐标为(3,1);
故答案为:(1,4),(3,1);
(2)根据平移可得点P平移后的对应点P1坐标为(a﹣4,a﹣5),
∴PP1的长为=,
故答案为:(a﹣4,a﹣5),;
(3)如图,△A2B2C2即为所求;
边CB在旋转过程中所扫过的面积==π.
24.如图所示,平面直角坐标系中,直线l1:y=﹣2x+3与直线l2:y=x+1相交于点A,直线l2与x轴相交于点B.过直线l2上的一点P(a,﹣1)作y轴的垂线,交直线l1于点C,连接BC.
(1)求点A的坐标;
(2)求△ABC的面积;
(3)将直线l1向下平移4个单位长度得到直线l3,设直线l3与y轴相交于点D,则直线l2上是否存在一点Q,使得△DPQ是以DP为腰的等腰三角形?若存在,请直接写出Q的坐标,若不存在,请说明理由.
【分析】(1)联立方程组可求解;
(2)分别求出点B,点C坐标,由三角形的面积公式可求解;
(3)先求出点D坐标,由等腰三角形的性质和两点之间的距离公式可求解.
解:(1)由题意可得:,
解得:,
∴点A(,);
(2)∵直线l2与x轴相交于点B,
∴点B(﹣1,0),
∵点P(a,﹣1)在直线l2上,
∴﹣1=a+1,
∴a=﹣2,
∴点P(﹣2,﹣1),
∴点C的纵坐标为﹣1,
∴﹣1=﹣2x+3,
∴x=2,
∴点C(2,﹣1),
如图,设直线l1与x轴相交于点H,
∴0=﹣2x+3,
∴x=,
∴点H(,0),
∴BH=,
∴△ABC的面积=××(+1)=;
(3)存在,理由如下:
∵将直线l1向下平移4个单位长度得到直线l3,
∴直线l3,的解析式为:y=﹣2x﹣1,
∴点D(0,﹣1),
如图,
∵点P(﹣2,﹣1),点D(0,﹣1),
∴PD⊥y轴,PD=2,
设点Q(a,a+1),
∵△DPQ是以DP为腰的等腰三角形,
∴PQ=PD=2或PD=QD=2,
当PQ=PD=2时,则(﹣2﹣a)2+(﹣1﹣a﹣1)2=4,
∴a=±﹣2,
∴点Q(﹣2,﹣1)或(﹣﹣2,﹣﹣1);
当PD=QD=2时,则(a﹣0)2+(﹣1﹣a﹣1)2=4,
∴a=0或﹣2(不合题意舍去),
∴点Q(0,1),
综上所述:点Q坐标为:(﹣2,﹣1)或(﹣﹣2,﹣﹣1)或(0,1).
25.“红缬退风花著子,绿针浮水稻抽秧”这是宋朝诗人姚孝锡所作.诗中咏诵的“水稻”是我国种植的重要经济作物.某村在政府的扶持下建起了水稻种植基地,准备种植甲,乙两种水稻,若种植20亩甲种水稻和30亩乙种水稻,共需投入22万元;若种植30亩甲种水稻和20亩乙种水稻,共需投入23万元.
(1)种植甲,乙两种水稻,每亩各需投入多少万元?
(2)经测算,种植甲种水稻每亩可获利a(a>0且a为常数)万元,种植乙种水稻每亩可获利0.8万元,村里投入50万元用来种植这两种水稻,若要求甲种水稻的种植面积不能少于乙种水稻种植面积的倍,且不能多于乙种水稻种植面积的倍.设种植乙种水稻m亩,该村种植两种水稻共获利W万元,请求出W关于m的函数表达式,并求出最大获利(用含a的代数式表示).
【分析】(1)根据题意列二元一次方程组即可得到答案;
(2)由题意甲种水稻的种植面积为=(100﹣0.8m)亩,根据甲种水稻的种植面积不能少于乙种水稻种植面积的倍,且不能多于乙种水稻种植面积的倍,可得25≤m≤50,而W=(100﹣0.8m) a+0.8m=(0.8﹣0.8a)m+100a,当0<a<1时,m=50时,最大获利W为(0.8﹣0.8a)×50+100a=(60a+40)万元,当a=1时,W=100a(万元),当a>1时,m=25时,最大获利W为(0.8﹣0.8a)×25+100a=(80a+20)万元.
解:(1)设甲种水稻每亩需投入x万元,乙种水稻每亩需投入y万元,
根据题意得,
解得,
答:甲种水稻每亩需投入0.5万元,乙种水稻每亩需投入0.4万元;
(2)由题意甲种水稻的种植面积为=(100﹣0.8m)亩,
∵甲种水稻的种植面积不能少于乙种水稻种植面积的倍,且不能多于乙种水稻种植面积的倍,
∴m≤100﹣0.8m≤m,
解得25≤m≤50,
∵种植甲种水稻每亩可获利a(a>0且a为常数)万元,种植乙种水稻每亩可获利0.8万元,
∴W=(100﹣0.8m) a+0.8m=(0.8﹣0.8a)m+100a,
当0<a<1时,0.8﹣0.8a>0,W随m的增大而增大,
∴m=50时,最大获利W为(0.8﹣0.8a)×50+100a=(60a+40)万元,
当a=1时,W=100a(万元),
当a>1时,0.8﹣0.8a<0,W随m的增大而减小,
∴m=25时,最大获利W为(0.8﹣0.8a)×25+100a=(80a+20)万元,
综上所述,当0<a<1时,最大获利W为(60a+40)万元,当a=1时,W=100a万元,当a>1时,最大获利W为(80a+20)万元.
26.在平行四边形ABCD中,连接BD,若BD⊥CD,点E为边AD上一点,连接CE.
(1)如图1,点G在BD上,且DG=DC,连接CG,过G作GH⊥CE于点H,连接DH并延长交AB于点M,若HG=BM,求证:BM+DH=DB;
(2)如图2,∠ABC=120°,AB=,点N在BC边上,BC=4CN,若CE是∠DCB的角平分线,线段PQ(点P在点Q的左侧)在线段CE上运动,PQ=,连接BP、NQ,请直接写出BP+PQ+QN的最小值.
【分析】(1)如图1,过点D作DF⊥DM交CE于点F,设CE与BD交于点K,先证明△DCF≌△DGH(ASA),进而证得△DFH是等腰直角三角形,得出FH=DH,再证明△DMB≌△CGH(AAS),推出CF=BM,即可证得结论;
(2)如图2,在CD上截取CG=CN,连接GQ,过点B作BF∥CE,使BF=PQ=,连接DF交CE于点T,连接QF,过点F作FM⊥BD于点M,过点G作GH⊥DF于点H,应用平行四边形的性质和含30°直角三角形三边关系可得:BC=2CD=2,利用勾股定理可得BD=,再利用含30°直角三角形三边关系可得:BM=BF=,FM=BM=,进而可得DM=,求得:FG=,再证四边形BPQF是平行四边形,得出BP=FQ,再证明△CNQ≌△CGQ(SAS),得出QN=QG,根据FQ+QG≥FG,可得出:当点Q在线段FG上时,FQ+QG的最小值为FG,即BP+QN的最小值为FG,即可求得BP+PQ+QN的最小值.
解:(1)如图1,过点D作DF⊥DM交CE于点F,设CE与BD交于点K,
∵BD⊥CD,DF⊥DM,GH⊥CE,
∴∠CDG=∠FDH=∠CHG=90°,
∴∠CDF=∠GDH,
∵∠DGH+∠HKG=∠DCF+∠DKC=90°,∠HKG=∠DKC,
∴∠DCF=∠DGH,
在△DCF和△DGH中,
,
∴△DCF≌△DGH(ASA),
∴DF=DH,CF=GH,
∵∠FDH=90°,
∴△DFH是等腰直角三角形,
∴∠DFH=∠DHF=45°,FH=DH,
∵DC=DG,∠CDG=90°,
∴∠CGD=DCG=45°,
∴∠CGD=∠DHF,
∵∠CGD+∠GCH+∠CKG=∠DHF+∠BDM+∠DKH=180°,∠CKG=∠DKH,
∴∠GCH=∠BDM,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DBM=∠CDG=90°=∠CHG,
在△DMB和△CGH中,
,
∴△DMB≌△CGH(AAS),
∴DB=CH,
∵CF=GH,BM=GH,
∴CF=BM,
∵CF+FH=CH,
∴BM+DH=DB;
(2)如图2,在CD上截取CG=CN,连接GQ,过点B作BF∥CE,使BF=PQ=,
连接DF交CE于点T,连接QF,过点F作FM⊥BD于点M,过点G作GH⊥DF于点H,
∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=,
∵∠ABC=120°,
∴∠BCD=180°﹣120°=60°,
∵BD⊥CD,CD=,
∴∠CBD=90°﹣60°=30°,
∴BC=2CD=2,
∴BD===,
∵CE平分∠DCB,
∴∠BCE=∠DCE=∠DCB=×60°=30°,
∵BF∥CE,
∴∠CBF=∠BCE=30°,
∴∠DBF=∠CBF+∠CBD=30°+30°=60°,
∵FM⊥BD,BF=,
∴BM=BF=×=,FM=BM=×=,
∴DM=BD﹣BM=﹣=,
∴DF===,
∵DF2+BF2=()2+()2=15,
∴DF2+BF2=BD2,
∴BF⊥DF,
∵BF∥CE,
∴CE⊥DF,
∵∠DCE=30°,
∴∠CDF=90°﹣30°=60°,
∵BC=2,BC=4CN,
∴CN=×2=,
∴CG=CN=,
∴DG=CD﹣CG=﹣=,
∵GH⊥DF,∠CDF=60°,
∴DH=DG=×=,GH=DH=×=,
∴FH=DF﹣DH=﹣=,
∴FG===,
∵BF∥CE,BF=PQ,
∴四边形BPQF是平行四边形,
∴BP=FQ,
在△CNQ和△CGQ中,
,
∴△CNQ≌△CGQ(SAS),
∴QN=QG,
∵FQ+QG≥FG,
∴当点Q在线段FG上时,FQ+QG的最小值为FG,
∴BP+QN的最小值为FG,
∵PQ=,FG=,
∴BP+PQ+QN的最小值为FG+PQ=+=,
故BP+PQ+QN的最小值为.
同课章节目录
