三角形的相似判定(5)HL及总结
文档属性
| 名称 | 三角形的相似判定(5)HL及总结 |  | |
| 格式 | zip | ||
| 文件大小 | 743.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-25 09:07:51 | ||
图片预览



文档简介
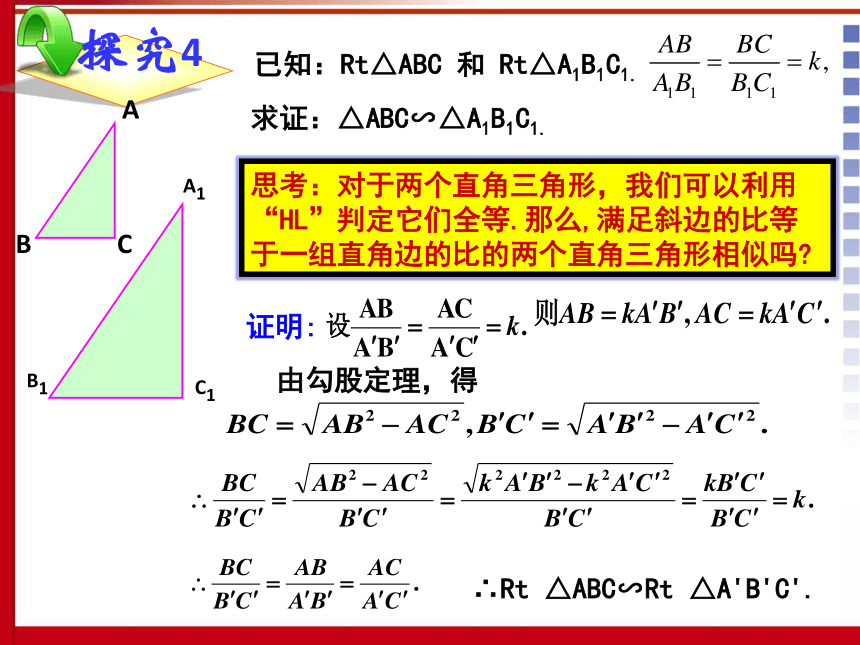
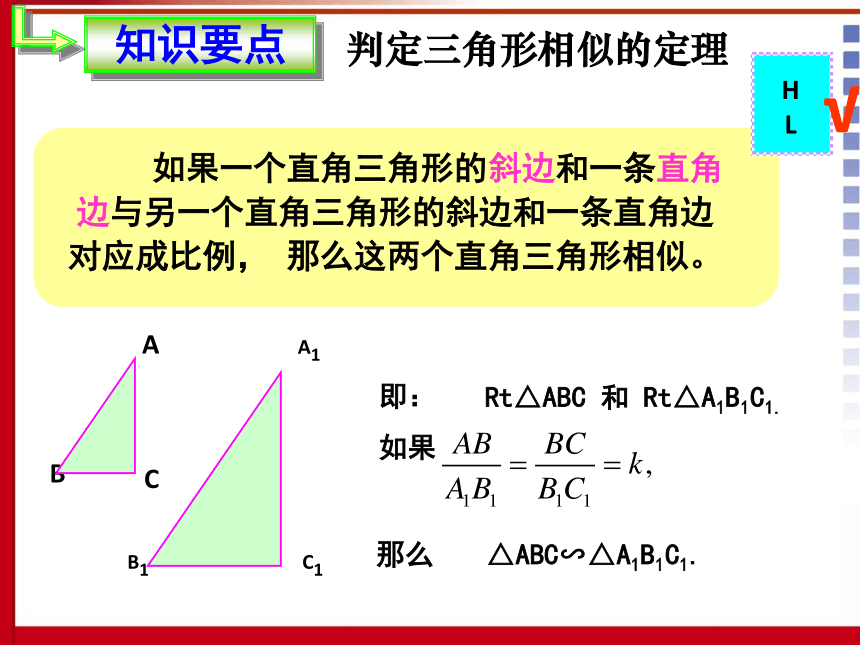
课件25张PPT。27.2.1 相似三角形的判定(hl)三角形相似的识别方法有那些?方法1:通过定义方法5:通过两角对应相等。温故知新方法2:平行于三角形一边的直线。方法3:三边对应成比例。方法4:两边对应成比例且夹角。已知:Rt△ABC 和 Rt△A1B1C1.求证:△ABC∽△A1B1C1.思考:对于两个直角三角形,我们可以利用“HL”判定它们全等.那么,满足斜边的比等于一组直角边的比的两个直角三角形相似吗?证明:由勾股定理,得∴Rt △ABC∽Rt △A'B'C'. 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似。判定三角形相似的定理△ABC∽△A1B1C1.即:
如果那么√Rt△ABC 和 Rt△A1B1C1.例1、RtΔABC和RtΔA'B'C'中,∠C=∠C'=90°.依据下列各组条件判定这两个三角形是不是相似,并说明为什么:
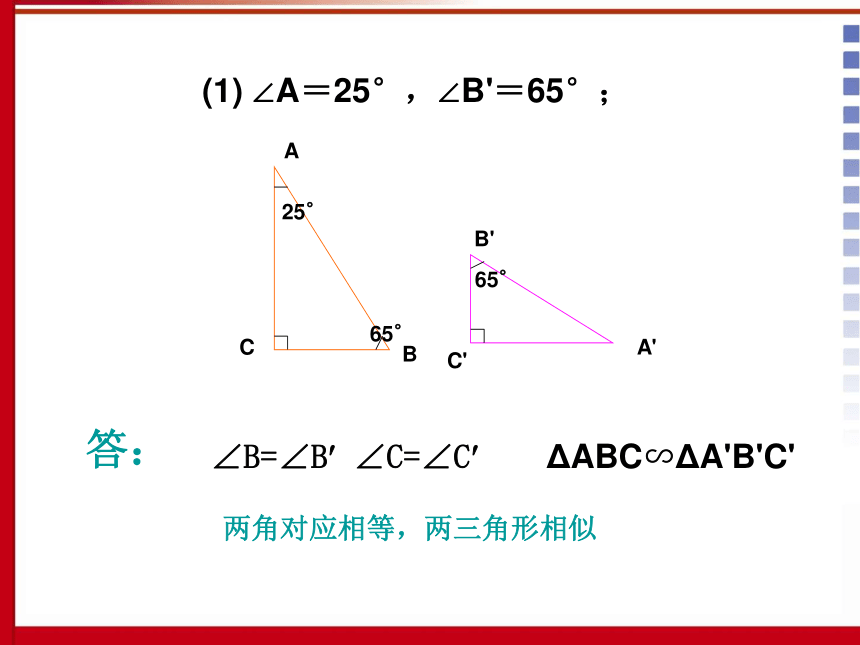
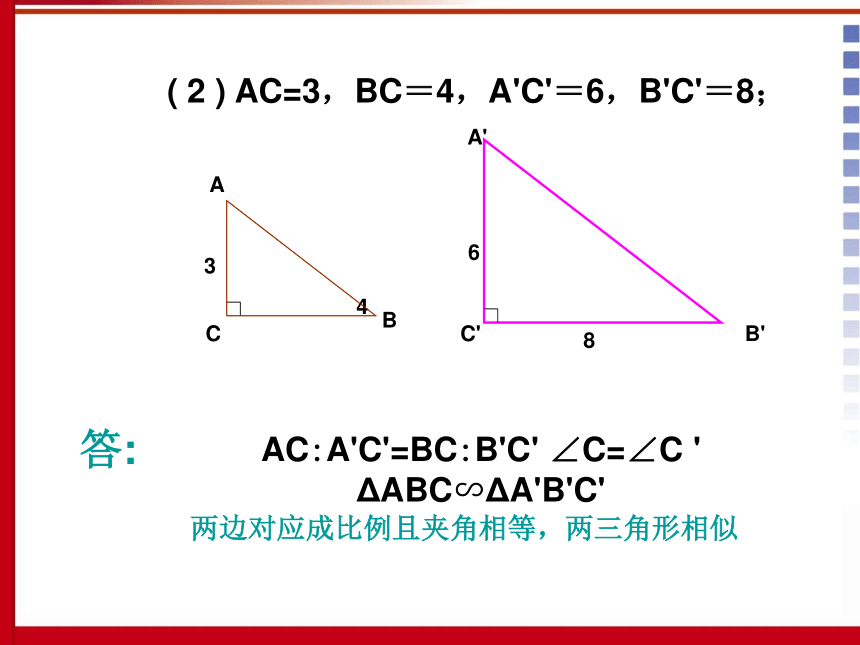
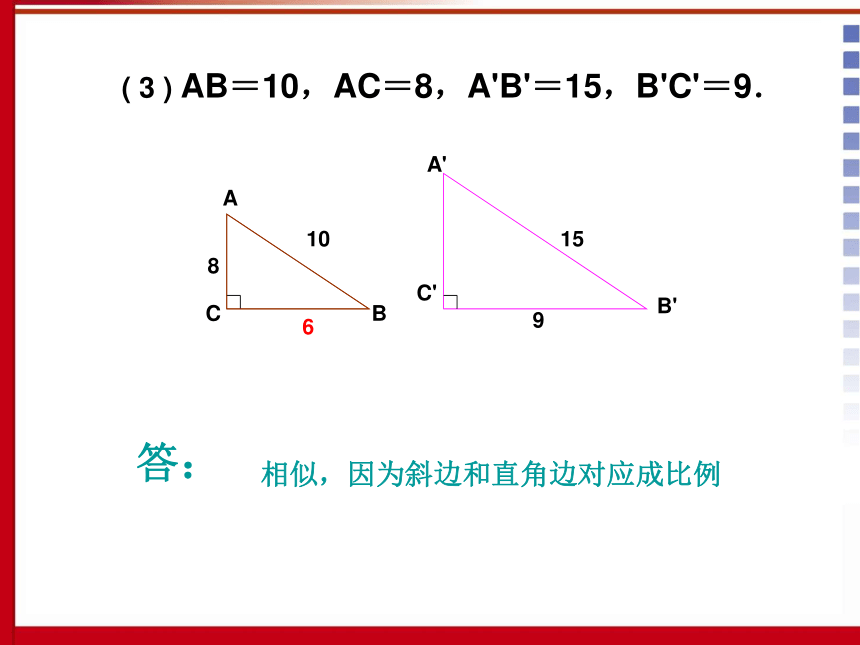
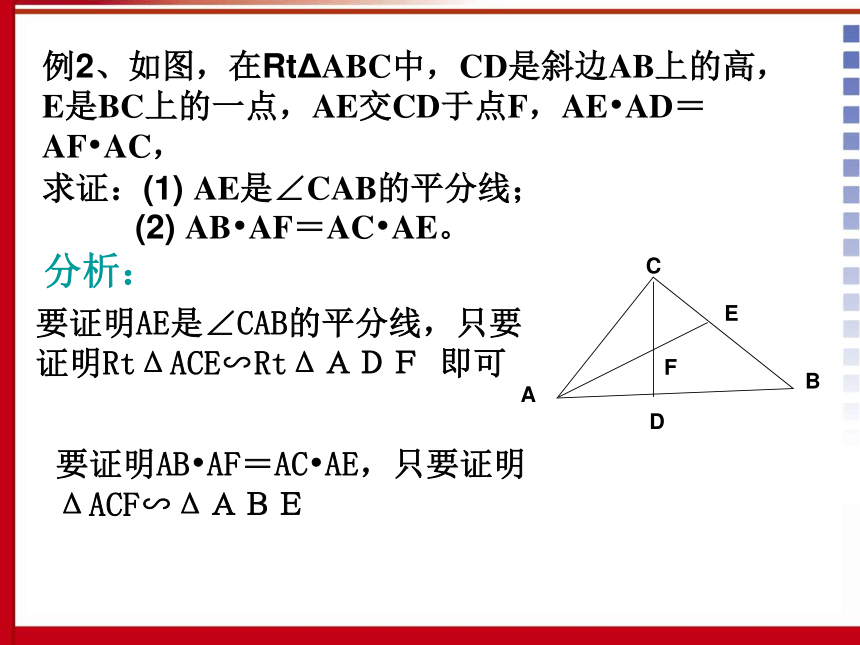
课堂练习(1) ∠A=25°,∠B'=65°;(2) AC=3,BC=4,A'C'=6,B'C'=8;(3) AB=10,AC=8,A'B'=15,B'C'=9.ACBB'A'C'25°65°答:两角对应相等,两三角形相似65°∠B=∠B? ∠C=∠C? ΔABC∽ΔA'B'C'(1) ∠A=25°,∠B'=65°;ABC4A'C'B'683两边对应成比例且夹角相等,两三角形相似答:AC:A'C'=BC:B'C' ∠C=∠C ' ΔABC∽ΔA'B'C'( 2 ) AC=3,BC=4,A'C'=6,B'C'=8;A'B'C'159答:相似,因为斜边和直角边对应成比例( 3 ) AB=10,AC=8,A'B'=15,B'C'=9.CAB1086例2、如图,在RtΔABC中,CD是斜边AB上的高,E是BC上的一点,AE交CD于点F,AE?AD=AF?AC,
求证:(1) AE是∠CAB的平分线;
(2) AB?AF=AC?AE。ABCDEF分析:要证明AE是∠CAB的平分线,只要证明RtΔACE∽RtΔADF 即可要证明AB?AF=AC?AE,只要证明ΔACF∽ΔABEΔAEC∽ΔAFD∠CAE=∠BAEAE是∠CAB的角平分线∠ACD+∠CAB=90°∠B+∠CAB=90°∠ACD=∠B∠CAE=∠EABΔACF∽ΔABEAB?AF=AC?AE(2)(1)又证明ABCDEF相似三角形的判定定理:定理3:两角对应相等,两三角形相似。定理2:两边对应成比例且夹角相等,两三角形相似。定理1:三边对应成比例,两三角形相似。知识回顾例1:已知如图,AB∥A'B',BC∥B'C' 求证:△ABC∽△A'B'C’ 证明:
∵AB∥A’B’ ∴∠1=∠2,
?A’B’/AB=OB’/OB ??? ∵BC∥B’C’ ∴∠3=∠4,
B’C’/BC = ?OB’/OB? ∴∠ABC=∠A’B’C ∴ ?A’B’/AB =B’C’/BC ????
∴△ABC∽△A'B'C' BcAB’C’OA’13242.已知:如图,△ABC中,P是AB边上的一点,连结CP.满足什么条件时△ ACP∽△ABC. 解:⑴∵∠A= ∠A,∴当∠1= ∠ACB (或∠2= ∠B)时,△ ACP∽△ABC
⑵ ∵∠A= ∠A,∴当AC:AP=AB:AC时,
△ ACP∽△ABC
⑶ ∵∠A= ∠A,
当∠4+∠ACB=180°时, △ ACP∽△ABC答:当∠1= ∠ACB 或∠2= ∠B 或AC:AP=AB:AC或∠4+∠ACB=180°时,△ ACP∽△ABC.3. D为△ABC中AB边上一点,∠ACD= ∠ ABC.
求证:AC2=AD·AB分析:要证明AC2=AD·AB,需
要先将乘积式改写为比例
式 ,再证明AC、
AD、AB所在的两个三角形相
似。由已知两个三角形有二个
角对应相等,所以两三角形相
似,本题可证。证明:∵ ∠ACD= ∠ ABC
∠A = ∠ A
∴ △ABC △ACD
∴
∴ AC2=AD·AB4. △ABC中,∠ BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E, 交AB于D,连AM.
求证:① △ MAD ∽△ MEA ② AM2=MD · ME分析:已知中与线段有关的条件仅有AM=BC/2=BM=MC,所以首先考虑用两个角对应相等去判定两个三角形相似。AM是△ MAD 与△ MEA 的公共边,故是对应边MD、ME的比例中项。证明:①∵∠BAC=90°
M为斜边BC中点
∴AM=BM=BC/2
∴ ∠B= ∠MAD
又 ∵ ∠B+ ∠BDM=90°
∠E+ ∠ADE= 90°
∠BDM= ∠ADE∴∠B=∠E
∴∠MAD= ∠E
又 ∵ ∠DMA= ∠AME
∴△MAD∽ △MEA② ∵ △MAD∽ △MEA
∴
即AM2=MD·MEACDEM5. 如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO · EC.分析:欲证 ED2=EO·EC,即证:
,只需证DE、EO、EC
所在的三角形相似。
证明:∵ AB∥CD
∴ ∠C=∠A
∵ AO=OB,DF=FB
∴ ∠A= ∠B, ∠B= ∠FDB
∴ ∠C= ∠FDB
又 ∵ ∠DEO= ∠DEC
∴ △EDC∽△EOD
∴ ,即 ED2=EO · EC
6. 过◇ABCD的一个顶点A作一直线分别交对角线BD、边 BC、边DC的延长线于E、F、G .
求证:EA2 = EF· EG . 分析:要证明
EA2 = EF· EG ,
即 证明 成
立,而EA、EG、EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段、换比例的方法。可证明:△AED∽△FEB, △AEB ∽ △GED.证明:∵ AD∥BF AB∥BC
∴△AED ∽△FEB
△AEB ∽△GED
∴
∴7. △ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC证明:
∵BD⊥AC,CE⊥AB
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°
∴ ∠ABD= ∠ACE
又∵ ∠A= ∠A
∴△ ABD ∽ △ ACE
∴
∵ ∠A= ∠A
∴ △ ADE ∽ △ ABC
如果那么√Rt△ABC 和 Rt△A1B1C1.例1、RtΔABC和RtΔA'B'C'中,∠C=∠C'=90°.依据下列各组条件判定这两个三角形是不是相似,并说明为什么:
课堂练习(1) ∠A=25°,∠B'=65°;(2) AC=3,BC=4,A'C'=6,B'C'=8;(3) AB=10,AC=8,A'B'=15,B'C'=9.ACBB'A'C'25°65°答:两角对应相等,两三角形相似65°∠B=∠B? ∠C=∠C? ΔABC∽ΔA'B'C'(1) ∠A=25°,∠B'=65°;ABC4A'C'B'683两边对应成比例且夹角相等,两三角形相似答:AC:A'C'=BC:B'C' ∠C=∠C ' ΔABC∽ΔA'B'C'( 2 ) AC=3,BC=4,A'C'=6,B'C'=8;A'B'C'159答:相似,因为斜边和直角边对应成比例( 3 ) AB=10,AC=8,A'B'=15,B'C'=9.CAB1086例2、如图,在RtΔABC中,CD是斜边AB上的高,E是BC上的一点,AE交CD于点F,AE?AD=AF?AC,
求证:(1) AE是∠CAB的平分线;
(2) AB?AF=AC?AE。ABCDEF分析:要证明AE是∠CAB的平分线,只要证明RtΔACE∽RtΔADF 即可要证明AB?AF=AC?AE,只要证明ΔACF∽ΔABEΔAEC∽ΔAFD∠CAE=∠BAEAE是∠CAB的角平分线∠ACD+∠CAB=90°∠B+∠CAB=90°∠ACD=∠B∠CAE=∠EABΔACF∽ΔABEAB?AF=AC?AE(2)(1)又证明ABCDEF相似三角形的判定定理:定理3:两角对应相等,两三角形相似。定理2:两边对应成比例且夹角相等,两三角形相似。定理1:三边对应成比例,两三角形相似。知识回顾例1:已知如图,AB∥A'B',BC∥B'C' 求证:△ABC∽△A'B'C’ 证明:
∵AB∥A’B’ ∴∠1=∠2,
?A’B’/AB=OB’/OB ??? ∵BC∥B’C’ ∴∠3=∠4,
B’C’/BC = ?OB’/OB? ∴∠ABC=∠A’B’C ∴ ?A’B’/AB =B’C’/BC ????
∴△ABC∽△A'B'C' BcAB’C’OA’13242.已知:如图,△ABC中,P是AB边上的一点,连结CP.满足什么条件时△ ACP∽△ABC. 解:⑴∵∠A= ∠A,∴当∠1= ∠ACB (或∠2= ∠B)时,△ ACP∽△ABC
⑵ ∵∠A= ∠A,∴当AC:AP=AB:AC时,
△ ACP∽△ABC
⑶ ∵∠A= ∠A,
当∠4+∠ACB=180°时, △ ACP∽△ABC答:当∠1= ∠ACB 或∠2= ∠B 或AC:AP=AB:AC或∠4+∠ACB=180°时,△ ACP∽△ABC.3. D为△ABC中AB边上一点,∠ACD= ∠ ABC.
求证:AC2=AD·AB分析:要证明AC2=AD·AB,需
要先将乘积式改写为比例
式 ,再证明AC、
AD、AB所在的两个三角形相
似。由已知两个三角形有二个
角对应相等,所以两三角形相
似,本题可证。证明:∵ ∠ACD= ∠ ABC
∠A = ∠ A
∴ △ABC △ACD
∴
∴ AC2=AD·AB4. △ABC中,∠ BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E, 交AB于D,连AM.
求证:① △ MAD ∽△ MEA ② AM2=MD · ME分析:已知中与线段有关的条件仅有AM=BC/2=BM=MC,所以首先考虑用两个角对应相等去判定两个三角形相似。AM是△ MAD 与△ MEA 的公共边,故是对应边MD、ME的比例中项。证明:①∵∠BAC=90°
M为斜边BC中点
∴AM=BM=BC/2
∴ ∠B= ∠MAD
又 ∵ ∠B+ ∠BDM=90°
∠E+ ∠ADE= 90°
∠BDM= ∠ADE∴∠B=∠E
∴∠MAD= ∠E
又 ∵ ∠DMA= ∠AME
∴△MAD∽ △MEA② ∵ △MAD∽ △MEA
∴
即AM2=MD·MEACDEM5. 如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO · EC.分析:欲证 ED2=EO·EC,即证:
,只需证DE、EO、EC
所在的三角形相似。
证明:∵ AB∥CD
∴ ∠C=∠A
∵ AO=OB,DF=FB
∴ ∠A= ∠B, ∠B= ∠FDB
∴ ∠C= ∠FDB
又 ∵ ∠DEO= ∠DEC
∴ △EDC∽△EOD
∴ ,即 ED2=EO · EC
6. 过◇ABCD的一个顶点A作一直线分别交对角线BD、边 BC、边DC的延长线于E、F、G .
求证:EA2 = EF· EG . 分析:要证明
EA2 = EF· EG ,
即 证明 成
立,而EA、EG、EF三条线段在同一直线上,无法构成两个三角形,此时应采用换线段、换比例的方法。可证明:△AED∽△FEB, △AEB ∽ △GED.证明:∵ AD∥BF AB∥BC
∴△AED ∽△FEB
△AEB ∽△GED
∴
∴7. △ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC证明:
∵BD⊥AC,CE⊥AB
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°
∴ ∠ABD= ∠ACE
又∵ ∠A= ∠A
∴△ ABD ∽ △ ACE
∴
∵ ∠A= ∠A
∴ △ ADE ∽ △ ABC
