华东师大版八年级下册数学 复习题 课件 (共9张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 复习题 课件 (共9张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 112.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 07:05:23 | ||
图片预览

文档简介
(共9张PPT)
复习题
动手折一折
如图矩形ABCD,在边BC上找一点E ,边AD上找一点F , 将矩形沿着直线EF折叠,使点A对应点A′落在BC边上.
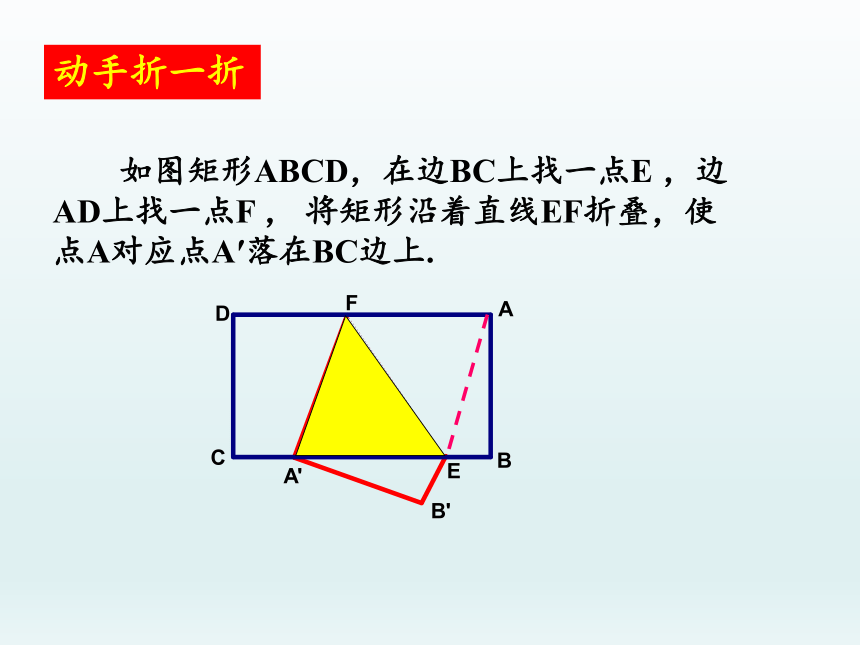
动手折一折
如图矩形ABCD,在边BC上找一点E ,边AD上找一点F , 将矩形沿着直线EF折叠,使点A对应点A′落在BC边上.
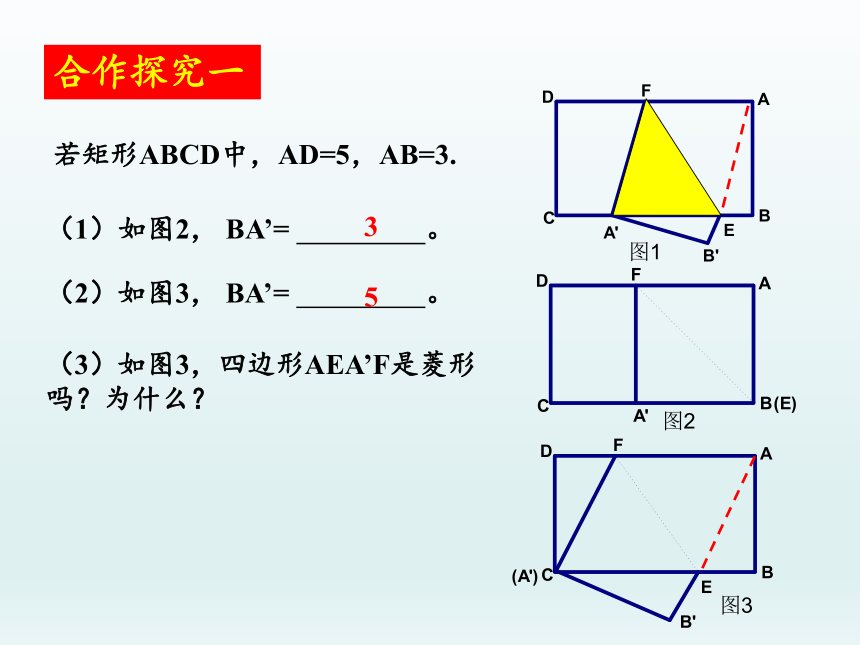
合作探究一
(3)如图3,四边形AEA’F是菱形吗?为什么?
图2
图1
图3
(1)如图2, BA’= 。
若矩形ABCD中,AD=5,AB=3.
3
(2)如图3, BA’= 。
5
合作探究二
(1)如图1,BA’ = 3 .
(2)如图5,BA’ = ,
AE= .
1
图1
图5
图4
矩形ABCD中,AD=5,AB=3,若点E,点F分别是边AB,边AD上的点,将⊿AEF沿EF对折,使点A落在边BC上,记为A′.观察图形,请回答下列问题:
在平面直角坐标系中,O为原点,矩形OABC的顶点A在x轴的正半轴上,点C在y轴的正半轴上, OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
如图
①求点B的坐标;
中考改编
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
B1
H
小结:
综上所述,可以发现折叠问题的解决,大都是以轴对称图形的性质作为切入点,而数形变化,是解决这类问题的突破口。有了“折”就有了“形”----轴对称图形、全等形;有了“折”就有了“数”----线段之间、角与角之间的数量关系。“折”就为“数”与“形”之间的转化搭起了桥梁。通过以上基本图形分析,不难看出解答此类问题的关键在于:因折叠产生的相等的线段和角。
已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 的图象与AC边交于点E.
请探索:是否存在这样的点
F,使得将△CEF沿EF对折
后,C点恰好落在OB上?
若存在,求出点F的坐标;
若不存在,请说明理由.
课后练习
谢 谢
复习题
动手折一折
如图矩形ABCD,在边BC上找一点E ,边AD上找一点F , 将矩形沿着直线EF折叠,使点A对应点A′落在BC边上.
动手折一折
如图矩形ABCD,在边BC上找一点E ,边AD上找一点F , 将矩形沿着直线EF折叠,使点A对应点A′落在BC边上.
合作探究一
(3)如图3,四边形AEA’F是菱形吗?为什么?
图2
图1
图3
(1)如图2, BA’= 。
若矩形ABCD中,AD=5,AB=3.
3
(2)如图3, BA’= 。
5
合作探究二
(1)如图1,BA’ = 3 .
(2)如图5,BA’ = ,
AE= .
1
图1
图5
图4
矩形ABCD中,AD=5,AB=3,若点E,点F分别是边AB,边AD上的点,将⊿AEF沿EF对折,使点A落在边BC上,记为A′.观察图形,请回答下列问题:
在平面直角坐标系中,O为原点,矩形OABC的顶点A在x轴的正半轴上,点C在y轴的正半轴上, OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
如图
①求点B的坐标;
中考改编
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
B1
H
小结:
综上所述,可以发现折叠问题的解决,大都是以轴对称图形的性质作为切入点,而数形变化,是解决这类问题的突破口。有了“折”就有了“形”----轴对称图形、全等形;有了“折”就有了“数”----线段之间、角与角之间的数量关系。“折”就为“数”与“形”之间的转化搭起了桥梁。通过以上基本图形分析,不难看出解答此类问题的关键在于:因折叠产生的相等的线段和角。
已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 的图象与AC边交于点E.
请探索:是否存在这样的点
F,使得将△CEF沿EF对折
后,C点恰好落在OB上?
若存在,求出点F的坐标;
若不存在,请说明理由.
课后练习
谢 谢
