北师大版2021-2022学年八年级数学下册1.4角平分线的的性质与判定同步练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022学年八年级数学下册1.4角平分线的的性质与判定同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 458.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 12:24:27 | ||
图片预览




文档简介
1.4角平分线的的性质与判定 北师大版
一、单选题
1.若三角形内一点到三边的距离相等,则这个点是( )
A.三条边的垂直平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条角平分线的交点
2.如图,点A在点O的北偏西的方向5km处,.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是( )
A.点B在点A的北偏东方向5km处
B.点B在点A的北偏东方向5km处
C.点B在点A的北偏东方向km处
D.点B在点A的北偏东方向km处
3.如图,在△ABC中,∠C =90°,AD平分∠BAC交BC于点D,若CD=9,则点D到斜边AB的距离为( )
A.4.5 B.9 C.18 D.20
4.如图,在△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,BC=8cm,BD:CD=3:4,则点D到AC的距离为( )cm.
A.3 B.4 C. D.
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则线段DE的长为( )
A. B.3 C. D.1
6.如图,已知在 A B C中,C D是A B边上的高线,B E平分∠A B C,交C D于点E, B C=10, D E=3,则 B C E的面积等于( )
A.6 B.9 C.15 D.1
7.如图,Rt△ABC中,∠C=90°,以点B为圆心,适当长为半径画弧,与∠ABC的两边相交于点E,F,分别以点E和点F为圆心,大于EF的长为半径画弧,两弧相交于点M,作射线BM,交AC于点D.若△BDC的面积为12,∠ABC=2∠A,则△ABC的面积为( )
A.24 B.36 C.12 D.48
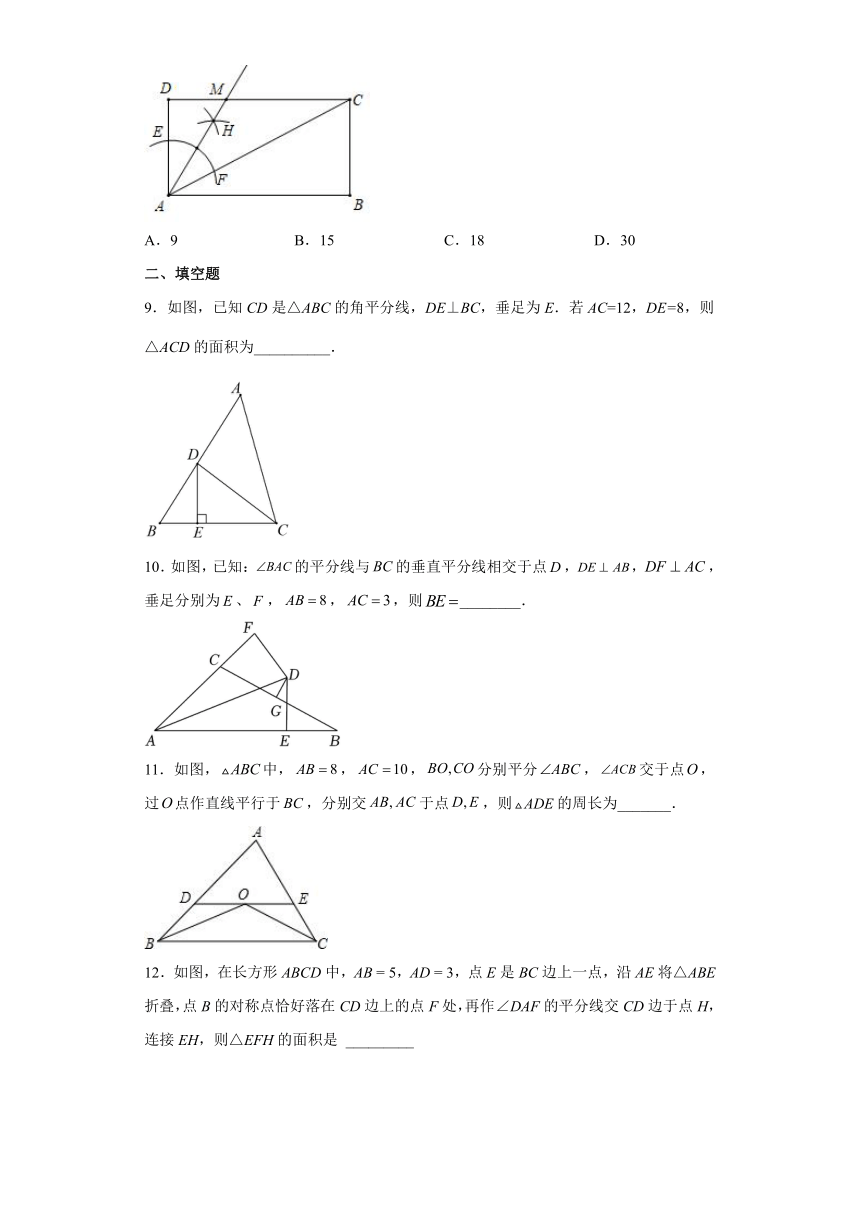
8.如图,在长方形中,连接,以为圆心适当长为半径画弧,分别交于点,分别以为圆心,大于的长为半径画弧,两弧在内交于点,画射线交于点.若,则的面积为( )
A.9 B.15 C.18 D.30
二、填空题
9.如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E.若AC=12,DE=8,则△ACD的面积为__________.
10.如图,已知:的平分线与的垂直平分线相交于点,,,垂足分别为、,,,则________.
11.如图,中,,,分别平分,交于点,过点作直线平行于,分别交于点,则的周长为_______.
12.如图,在长方形ABCD中,AB = 5,AD = 3,点E是BC边上一点,沿AE将△ABE折叠,点B的对称点恰好落在CD边上的点F处,再作∠DAF的平分线交CD边于点H,连接EH,则△EFH的面积是 _________
13.如图,∠AOB=90°,按以下步骤作图:
①以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
②分别以C、D为圆心,以大于的同样长为半径作弧,两弧交于点P;
③作射线OP.
如图,点M在射线OP上,过M作MH⊥OB于H,若MH=2,则OM=________.
三、解答题
14.如图,AB=AC,BD=DC,DF⊥AB,DE⊥AC,垂足分别是F,E.求证:DE=DF.
15.如图,在中,.
(1)过点作的平分线交于点(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
16.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线;
(2)若∠AOB=60°,请直接写出OE与EF之间的数量关系.
17.如图,在四边形ABCD中,AB=AD,BC>CD,AC平分∠BCD,过点A作AE⊥BC,垂足为点E.
(1)求证:CE=CDBE;
(2)如果CE=3BE,求的值.
试卷第1页,共3页
参考答案:
1.D
【解析】
解:根据角平分线的判定定理:到角两边距离相等的点在角平分线上,
∴到到三边的距离相等的点是三角形三个角的平分线交点.
故选择D.
2.D
【解析】
过A作AC∥OM交ON于C,作AD∥ON,如图:
∵∠MON=90°,∠AOC=30°,
∴∠AOM=120°,
由作图可知,OB平分∠AOM,
∴∠AOB=∠AOM=60°,
∴∠B=30°,
在Rt△AOB中,OB=2OA=10,
∴,
∵∠AOC=30°,∠ACO=90°,
∴∠CAO=60°,
∴∠DAB=90°-∠BAC=∠CAO=60°,
∴B在A北偏东60°方向km处,
故选:D.
3.B
【解析】
过点D作,交AB于点E,如下图
∵AD平分∠BAC交BC于点D,∠C =90°, CD=9,
∴,即点D到斜边AB的距离为:9
故选:B.
4.D
【解析】
解:∵BC=8cm,BD:CD=3:4,
∴BD=cm,
∵AD平分∠BAC,∠B=90°,
∴D到AC的距离等于BD,
∴D点到线段AC的距离为cm,
故选:D.
5.C
【解析】
解:如图,过点F作FG⊥AB于点G,
∵∠ACB=90°,CD⊥AB,
∴∠CDA=90°,
∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,
∵AF平分∠CAB,
∴∠CAF=∠FAD,
∴∠CFA=∠AED=∠CEF,
∴CE=CF,
∵AF平分∠CAB,∠ACF=∠AGF=90°,
∴FC=FG,
∵,
∴,
∴ ,
∵AC=3,AB=5,∠ACB=90°,
∴BC=4, ,
设 ,则 ,
∵ ,
∴ ,
解得: ,
∴ ,
∵ ,
∴ ,
∴ .
故选:C
6.C
【解析】
解:过E作EF⊥BC于F,
∵CD是AB边上的高线,BE平分∠ABC,
∴EF=DE=3,
∵BC=10,
∴△BCE的面积为×BC×EF=15,
故选:C.
7.B
【解析】
解:根据题意得,BD平分∠ABC
∠ABC=2∠A,
若△BDC的面积为12
故选:B.
8.B
【解析】
解:过点作交于点,
根据题意可得平分角,
∵,,
∴,
∴,
故选:B.
9.48
【解析】
解:过D点作DF⊥AC于F,如下图所示:
∵CD是∠ACB的角平分线,DE⊥BC,DF⊥AC,
∴DE=DF=8,
∴,
故答案为:48.
10.##2.5
【解析】
解:连接,,
是的平分线,,,
,,,
在和中,
,
,
,
是的垂直平分线,
,
在和中,
,
,
,
,
,,
.
故答案为:.
11.18
【解析】
解:
∵BO平分,CO平分,
∴,,
∵,
∴,,
∴,,
∴,,
∴的周长为:
,
,
,
,
,
.
故答案是:18.
12.##
【解析】
解: 长方形ABCD,折叠,
设 则
即
如图,过作于 而平分
经检验符合题意;
故答案为:.
13.
【解析】
解:由题意可得OP是∠AOB的角平分线,即∠MOH=∠AOB=45°
∵MH⊥OB
∴∠OMH=45°
∴△OMH是等腰直角三角形
∴OH=MH=2,
∴OM=.
故答案是.
14.证明见解析.
【解析】
证明:在和中,,
,
,即是的角平分线,
,
.
15.(1)见解析
(2)24
【解析】
(1)
∠ABC的平分线如图所示.
(2)
作DH⊥AB于H.
∵BD平分∠ABC,DC⊥BC,DH⊥AB,
∴CD=DH=3,
∴△ABC的面积=S△BCD+S△ABD=BC CD+AB DH=×3BC+×3AB=×3(BC+AB)=×3×16=24.
16.(1)见解析
(2)OE=4EF
【解析】
(1)
证明:∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,
∵OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)
解:∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
17.(1)证明见详解;
(2)=.
【解析】
(1)
证明:过点A作AF⊥CD交CD延长线于F,
∵AC平分∠BCD,AE⊥BC,AF⊥CD,
∴AE=AF,∠AEB=∠AFD=90°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
在Rt△ACE和Rt△ACF中,
,
∴Rt△ACE≌Rt△ACF(HL),
∴CE=CF,
∴CE=CF=CD+DF=CD+BE;
(2)
解:BC=BE+EC=BE+3BE=4BE,
∴S△ABC=,
∴CD=CF-FD=CE-BE=3BE-BE=2BE,
∴S△ADC=,
∴=.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.若三角形内一点到三边的距离相等,则这个点是( )
A.三条边的垂直平分线的交点 B.三条中线的交点
C.三条高的交点 D.三条角平分线的交点
2.如图,点A在点O的北偏西的方向5km处,.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是( )
A.点B在点A的北偏东方向5km处
B.点B在点A的北偏东方向5km处
C.点B在点A的北偏东方向km处
D.点B在点A的北偏东方向km处
3.如图,在△ABC中,∠C =90°,AD平分∠BAC交BC于点D,若CD=9,则点D到斜边AB的距离为( )
A.4.5 B.9 C.18 D.20
4.如图,在△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,BC=8cm,BD:CD=3:4,则点D到AC的距离为( )cm.
A.3 B.4 C. D.
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则线段DE的长为( )
A. B.3 C. D.1
6.如图,已知在 A B C中,C D是A B边上的高线,B E平分∠A B C,交C D于点E, B C=10, D E=3,则 B C E的面积等于( )
A.6 B.9 C.15 D.1
7.如图,Rt△ABC中,∠C=90°,以点B为圆心,适当长为半径画弧,与∠ABC的两边相交于点E,F,分别以点E和点F为圆心,大于EF的长为半径画弧,两弧相交于点M,作射线BM,交AC于点D.若△BDC的面积为12,∠ABC=2∠A,则△ABC的面积为( )
A.24 B.36 C.12 D.48
8.如图,在长方形中,连接,以为圆心适当长为半径画弧,分别交于点,分别以为圆心,大于的长为半径画弧,两弧在内交于点,画射线交于点.若,则的面积为( )
A.9 B.15 C.18 D.30
二、填空题
9.如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E.若AC=12,DE=8,则△ACD的面积为__________.
10.如图,已知:的平分线与的垂直平分线相交于点,,,垂足分别为、,,,则________.
11.如图,中,,,分别平分,交于点,过点作直线平行于,分别交于点,则的周长为_______.
12.如图,在长方形ABCD中,AB = 5,AD = 3,点E是BC边上一点,沿AE将△ABE折叠,点B的对称点恰好落在CD边上的点F处,再作∠DAF的平分线交CD边于点H,连接EH,则△EFH的面积是 _________
13.如图,∠AOB=90°,按以下步骤作图:
①以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
②分别以C、D为圆心,以大于的同样长为半径作弧,两弧交于点P;
③作射线OP.
如图,点M在射线OP上,过M作MH⊥OB于H,若MH=2,则OM=________.
三、解答题
14.如图,AB=AC,BD=DC,DF⊥AB,DE⊥AC,垂足分别是F,E.求证:DE=DF.
15.如图,在中,.
(1)过点作的平分线交于点(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
16.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线;
(2)若∠AOB=60°,请直接写出OE与EF之间的数量关系.
17.如图,在四边形ABCD中,AB=AD,BC>CD,AC平分∠BCD,过点A作AE⊥BC,垂足为点E.
(1)求证:CE=CDBE;
(2)如果CE=3BE,求的值.
试卷第1页,共3页
参考答案:
1.D
【解析】
解:根据角平分线的判定定理:到角两边距离相等的点在角平分线上,
∴到到三边的距离相等的点是三角形三个角的平分线交点.
故选择D.
2.D
【解析】
过A作AC∥OM交ON于C,作AD∥ON,如图:
∵∠MON=90°,∠AOC=30°,
∴∠AOM=120°,
由作图可知,OB平分∠AOM,
∴∠AOB=∠AOM=60°,
∴∠B=30°,
在Rt△AOB中,OB=2OA=10,
∴,
∵∠AOC=30°,∠ACO=90°,
∴∠CAO=60°,
∴∠DAB=90°-∠BAC=∠CAO=60°,
∴B在A北偏东60°方向km处,
故选:D.
3.B
【解析】
过点D作,交AB于点E,如下图
∵AD平分∠BAC交BC于点D,∠C =90°, CD=9,
∴,即点D到斜边AB的距离为:9
故选:B.
4.D
【解析】
解:∵BC=8cm,BD:CD=3:4,
∴BD=cm,
∵AD平分∠BAC,∠B=90°,
∴D到AC的距离等于BD,
∴D点到线段AC的距离为cm,
故选:D.
5.C
【解析】
解:如图,过点F作FG⊥AB于点G,
∵∠ACB=90°,CD⊥AB,
∴∠CDA=90°,
∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,
∵AF平分∠CAB,
∴∠CAF=∠FAD,
∴∠CFA=∠AED=∠CEF,
∴CE=CF,
∵AF平分∠CAB,∠ACF=∠AGF=90°,
∴FC=FG,
∵,
∴,
∴ ,
∵AC=3,AB=5,∠ACB=90°,
∴BC=4, ,
设 ,则 ,
∵ ,
∴ ,
解得: ,
∴ ,
∵ ,
∴ ,
∴ .
故选:C
6.C
【解析】
解:过E作EF⊥BC于F,
∵CD是AB边上的高线,BE平分∠ABC,
∴EF=DE=3,
∵BC=10,
∴△BCE的面积为×BC×EF=15,
故选:C.
7.B
【解析】
解:根据题意得,BD平分∠ABC
∠ABC=2∠A,
若△BDC的面积为12
故选:B.
8.B
【解析】
解:过点作交于点,
根据题意可得平分角,
∵,,
∴,
∴,
故选:B.
9.48
【解析】
解:过D点作DF⊥AC于F,如下图所示:
∵CD是∠ACB的角平分线,DE⊥BC,DF⊥AC,
∴DE=DF=8,
∴,
故答案为:48.
10.##2.5
【解析】
解:连接,,
是的平分线,,,
,,,
在和中,
,
,
,
是的垂直平分线,
,
在和中,
,
,
,
,
,,
.
故答案为:.
11.18
【解析】
解:
∵BO平分,CO平分,
∴,,
∵,
∴,,
∴,,
∴,,
∴的周长为:
,
,
,
,
,
.
故答案是:18.
12.##
【解析】
解: 长方形ABCD,折叠,
设 则
即
如图,过作于 而平分
经检验符合题意;
故答案为:.
13.
【解析】
解:由题意可得OP是∠AOB的角平分线,即∠MOH=∠AOB=45°
∵MH⊥OB
∴∠OMH=45°
∴△OMH是等腰直角三角形
∴OH=MH=2,
∴OM=.
故答案是.
14.证明见解析.
【解析】
证明:在和中,,
,
,即是的角平分线,
,
.
15.(1)见解析
(2)24
【解析】
(1)
∠ABC的平分线如图所示.
(2)
作DH⊥AB于H.
∵BD平分∠ABC,DC⊥BC,DH⊥AB,
∴CD=DH=3,
∴△ABC的面积=S△BCD+S△ABD=BC CD+AB DH=×3BC+×3AB=×3(BC+AB)=×3×16=24.
16.(1)见解析
(2)OE=4EF
【解析】
(1)
证明:∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,
∵OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)
解:∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
17.(1)证明见详解;
(2)=.
【解析】
(1)
证明:过点A作AF⊥CD交CD延长线于F,
∵AC平分∠BCD,AE⊥BC,AF⊥CD,
∴AE=AF,∠AEB=∠AFD=90°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
在Rt△ACE和Rt△ACF中,
,
∴Rt△ACE≌Rt△ACF(HL),
∴CE=CF,
∴CE=CF=CD+DF=CD+BE;
(2)
解:BC=BE+EC=BE+3BE=4BE,
∴S△ABC=,
∴CD=CF-FD=CE-BE=3BE-BE=2BE,
∴S△ADC=,
∴=.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
