2021-2022学年八年级人教版数学下册18.2.1矩形课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年八年级人教版数学下册18.2.1矩形课时练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 176.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 16:55:58 | ||
图片预览


文档简介
18.2.1《矩形》课时练习
一、选择题
1.对角线相等且互相平分的四边形是( )
A.一般四边形 B.平行四边形 C.矩形 D.菱形
2.在□ABCD中,AC交BD于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的条件是( )
A.AB=AD B.OA=OB C.AC=BD D.DC⊥BC
3.在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③ B.①②④ C.②③④ D.①③④
4.如图,矩形ABCD的顶点A,B,C分别落在∠MON的边OM,ON上,若OA=OC,要求只用无刻度的直尺作∠MON的平分线.小明的作法如下:连接AC,BD交于点E,作射线OE,则射线OE平分∠MON.
有以下几条几何性质:
①矩形的四个角都是直角;②矩形的对角线互相平分;③等腰三角形的“三线合一”.
小明的作法依据是( )
A.①② B.①③ C.②③ D.①②③
5、如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
A.2对 B.3对 C.4对 D.5对
6.四边形不具有稳定性,如图,矩形ABCD当改变内角大小就变成平行四边形ABC'D',若∠D'AB=30°,则平行四边形ABC'D'的面积与矩形ABCD的面积之比是( )
A. B. C. D.1
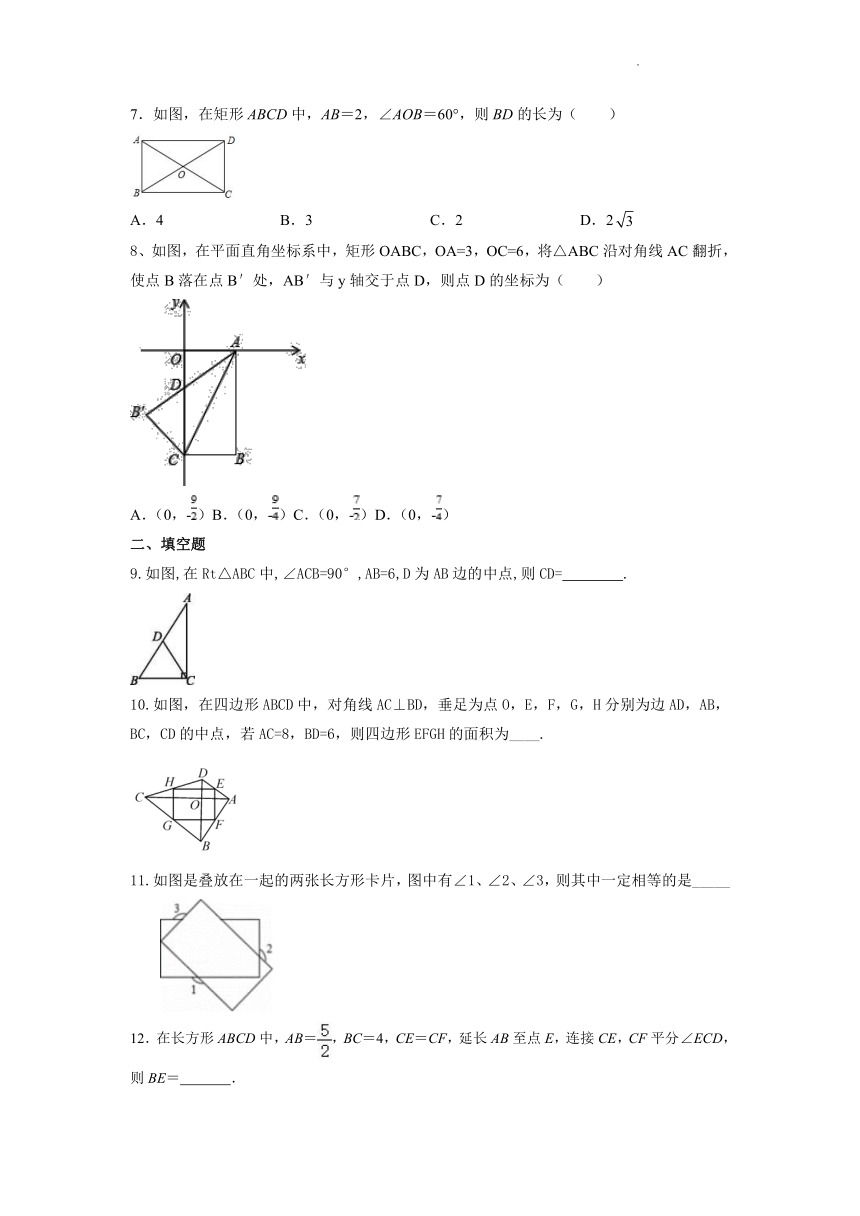
7.如图,在矩形ABCD中,AB=2,∠AOB=60°,则BD的长为( )
A.4 B.3 C.2 D.2
8、如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为( )
A.(0,-) B.(0,-) C.(0,-) D.(0,-)
二、填空题
9.如图,在Rt△ABC中,∠ACB=90°,AB=6,D为AB边的中点,则CD= .
10.如图,在四边形ABCD中,对角线AC⊥BD,垂足为点O,E,F,G,H分别为边AD,AB,BC,CD的中点,若AC=8,BD=6,则四边形EFGH的面积为____.
11.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____
12.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE= .
13.已知矩形ABCD,AB=8,AD=6,E是BC边上一点且CE=2BE,F是CD边的中点,连接AF、BF、DE相交于M、N两点,则△FMN的面积是 .
14.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD于点P,过点P作PQ⊥BC于点Q,则PQ= .
三、解答题
15.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE.
(2)连结DE,线段DE与AB之间有怎样的位置关系和数量关系?请证明你的结论.
16.如图,在Rt△ABC中,∠B=90°,AB=4,BC=3,阴影部分是一个长方形,AE=1,求阴影部分的面积.
17.如图,矩形ABCD中,E、F分别为边AD和BC上的点,BE=DF,求证:DE=BF.
18.如图所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=6,BC=10.求CE的长.
19.如图,在 ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.
20.如图,为矩形的对角线,于点,于点.
(1)求证:.
(2)求证:四边形是平行四边形.
参考答案
1.C 2.A 3.B 4.C 5、 C 6.A 7.A 8、B
9.3
10.12;
11.∠2=∠3
12:.
13.3.
14..
15. (1)证明:因为AB=AC,
所以∠B=∠ACB,
又因为AD是BC边上的中线,
所以AD⊥BC,即∠ADB=90°.
因为AE∥BC,所以∠EAC=∠ACB,
所以∠B=∠EAC.
因为CE⊥AE,所以∠CEA=90°,
所以∠ADB=∠CEA.
又AB=CA,
所以△ABD≌△CAE(A.A.S.).
(2)解:AB∥DE且AB=DE.
证明:由△ABD≌△CAE可得AE=BD,
又AE∥BD,所以四边形ABDE是平行四边形,所以AB∥DE且AB=DE.
16.解:在Rt△ABC中,∠B=90°,AB=4cm,BC=3cm,
由勾股定理得AB +BC =AC ,
即4 +3 =AC
∴AC=(cm),
∵AE=1cm,
∴长方形ACDE的面积为5×1=5(cm2)
17.证明:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠D=90°,
在Rt△ABE和Rt△CDF中,
,
∴Rt△ABE≌Rt△CDF(HL),
∴AE=CF,
∴DE=BF.
18.解:由翻折的性质可得:AD=AF=BC=10,DE=EF,
在Rt△ABF中可得:BF===8,
∴FC=BC﹣BF=2,
设CE=x,EF=DE=6﹣x,
在Rt△ECF中,EF2=EC2+CF2,即x2+4=(6﹣x)2,
解得x=,
∴CE的长为.
19.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD=BC,
∵BE=AB,
∴BE=CD,
∴四边形BECD是平行四边形,
∵AD=BC,AD=DE,
∴BC=DE,
∴四边形BECD是矩形;
(2)如图,
∵CD=2,
∴AB=BE=2,
∴AE=AB+BE=4,
∵AD=,∠ABD=90°,
∴BD==,
∴CE=,
∴AC===.
19 解:(1)设EF=x依题意知:△CDE≌△CFE,
∴DE=EF=x,CF=CD=6.
∵在Rt△ACD中,AC==10,
∴AF=AC﹣CF=4,AE=AD﹣DE=8﹣x.
在Rt△AEF中,有AE2=AF2+EF2
即(8﹣x)2=42+x2
解得x=3,即:EF=3.
(2)由(1)知:AE=8﹣3=5,
∴S梯形ABCE==(5+8)×6÷2=39.
20.解:(1)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
又BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
∴△ABE≌△CDF(ASA).
(2)∵△ABE≌△CDF,
∴BE=DF.
又BE⊥AC,DF⊥AC,
∴BE∥DF.
∴四边形BFDE是平行四边形.
一、选择题
1.对角线相等且互相平分的四边形是( )
A.一般四边形 B.平行四边形 C.矩形 D.菱形
2.在□ABCD中,AC交BD于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的条件是( )
A.AB=AD B.OA=OB C.AC=BD D.DC⊥BC
3.在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③ B.①②④ C.②③④ D.①③④
4.如图,矩形ABCD的顶点A,B,C分别落在∠MON的边OM,ON上,若OA=OC,要求只用无刻度的直尺作∠MON的平分线.小明的作法如下:连接AC,BD交于点E,作射线OE,则射线OE平分∠MON.
有以下几条几何性质:
①矩形的四个角都是直角;②矩形的对角线互相平分;③等腰三角形的“三线合一”.
小明的作法依据是( )
A.①② B.①③ C.②③ D.①②③
5、如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
A.2对 B.3对 C.4对 D.5对
6.四边形不具有稳定性,如图,矩形ABCD当改变内角大小就变成平行四边形ABC'D',若∠D'AB=30°,则平行四边形ABC'D'的面积与矩形ABCD的面积之比是( )
A. B. C. D.1
7.如图,在矩形ABCD中,AB=2,∠AOB=60°,则BD的长为( )
A.4 B.3 C.2 D.2
8、如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为( )
A.(0,-) B.(0,-) C.(0,-) D.(0,-)
二、填空题
9.如图,在Rt△ABC中,∠ACB=90°,AB=6,D为AB边的中点,则CD= .
10.如图,在四边形ABCD中,对角线AC⊥BD,垂足为点O,E,F,G,H分别为边AD,AB,BC,CD的中点,若AC=8,BD=6,则四边形EFGH的面积为____.
11.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____
12.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE= .
13.已知矩形ABCD,AB=8,AD=6,E是BC边上一点且CE=2BE,F是CD边的中点,连接AF、BF、DE相交于M、N两点,则△FMN的面积是 .
14.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD于点P,过点P作PQ⊥BC于点Q,则PQ= .
三、解答题
15.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE.
(2)连结DE,线段DE与AB之间有怎样的位置关系和数量关系?请证明你的结论.
16.如图,在Rt△ABC中,∠B=90°,AB=4,BC=3,阴影部分是一个长方形,AE=1,求阴影部分的面积.
17.如图,矩形ABCD中,E、F分别为边AD和BC上的点,BE=DF,求证:DE=BF.
18.如图所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=6,BC=10.求CE的长.
19.如图,在 ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.
20.如图,为矩形的对角线,于点,于点.
(1)求证:.
(2)求证:四边形是平行四边形.
参考答案
1.C 2.A 3.B 4.C 5、 C 6.A 7.A 8、B
9.3
10.12;
11.∠2=∠3
12:.
13.3.
14..
15. (1)证明:因为AB=AC,
所以∠B=∠ACB,
又因为AD是BC边上的中线,
所以AD⊥BC,即∠ADB=90°.
因为AE∥BC,所以∠EAC=∠ACB,
所以∠B=∠EAC.
因为CE⊥AE,所以∠CEA=90°,
所以∠ADB=∠CEA.
又AB=CA,
所以△ABD≌△CAE(A.A.S.).
(2)解:AB∥DE且AB=DE.
证明:由△ABD≌△CAE可得AE=BD,
又AE∥BD,所以四边形ABDE是平行四边形,所以AB∥DE且AB=DE.
16.解:在Rt△ABC中,∠B=90°,AB=4cm,BC=3cm,
由勾股定理得AB +BC =AC ,
即4 +3 =AC
∴AC=(cm),
∵AE=1cm,
∴长方形ACDE的面积为5×1=5(cm2)
17.证明:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠D=90°,
在Rt△ABE和Rt△CDF中,
,
∴Rt△ABE≌Rt△CDF(HL),
∴AE=CF,
∴DE=BF.
18.解:由翻折的性质可得:AD=AF=BC=10,DE=EF,
在Rt△ABF中可得:BF===8,
∴FC=BC﹣BF=2,
设CE=x,EF=DE=6﹣x,
在Rt△ECF中,EF2=EC2+CF2,即x2+4=(6﹣x)2,
解得x=,
∴CE的长为.
19.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD=BC,
∵BE=AB,
∴BE=CD,
∴四边形BECD是平行四边形,
∵AD=BC,AD=DE,
∴BC=DE,
∴四边形BECD是矩形;
(2)如图,
∵CD=2,
∴AB=BE=2,
∴AE=AB+BE=4,
∵AD=,∠ABD=90°,
∴BD==,
∴CE=,
∴AC===.
19 解:(1)设EF=x依题意知:△CDE≌△CFE,
∴DE=EF=x,CF=CD=6.
∵在Rt△ACD中,AC==10,
∴AF=AC﹣CF=4,AE=AD﹣DE=8﹣x.
在Rt△AEF中,有AE2=AF2+EF2
即(8﹣x)2=42+x2
解得x=3,即:EF=3.
(2)由(1)知:AE=8﹣3=5,
∴S梯形ABCE==(5+8)×6÷2=39.
20.解:(1)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
又BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
∴△ABE≌△CDF(ASA).
(2)∵△ABE≌△CDF,
∴BE=DF.
又BE⊥AC,DF⊥AC,
∴BE∥DF.
∴四边形BFDE是平行四边形.
