2021—2022学年学苏科版数学七年级下册7.1探索直线平行的条件阶段练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年学苏科版数学七年级下册7.1探索直线平行的条件阶段练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 378.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 17:00:02 | ||
图片预览


文档简介
第七章《平面图形的认识(二)》阶段练习(7.1)
一、单选题
1.如图,直线a、b被直线c所截.若∠1=55°,则∠2的度数是( )时能判定a∥b.
A.35° B.45° C.125° D.145°
2.如图点E在BC的延长线上,则下列条件中,不能判定ABCD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
3.如图所示,下列推理正确的是 ( )
A.因为∠1=∠4,所以BC∥AD B.因为∠2=∠3,所以AB∥CD
C.因为AD∥BC,所以∠BCD+∠ADC=180° D.因为∠1+∠2+∠C=180°,所以BC∥AD
(第1题图) (第2题图) (第3题图)
4.如图,下列说法错误的是( ).
A.与是内错角 B.与是同位角 C.与是内错角 D.与是同旁内角
5.如图,下列四个结论:①∠1=∠3;②∠B=∠5;③∠B+∠BAD=180 ;④∠2=∠4;⑤∠D+∠BCD=180 .能判断AB∥CD的个数有 ( )
A.2个 B.3个 C.4个 D.5个
6.如图,在四边形ABCD中,点E在线段DC的延长线上,能使直线AD∥BC的条件有( )(1)∠D=∠BCE,(2)∠B=∠BCE,(3)∠A+∠B=180°,(4)∠A+∠D=180°,(5)∠B=∠D
A.1个 B.2个 C.3个 D.4个
(第4题图) (第5题图) (第6题图)
7.如图(1),在中,,边绕点按逆时针方向旋转一周回到原来的位置.在旋转的过程中(图(2)),当( )时,.
A.42° B.138° C.42°或138° D.42°或128°
8.如图,将△ABE向右平移2 cm得到△DCF,如果△ABE的周长是16 cm,那么四边形ABFD的周长是 ( )
A.16 cm B.18 cm C.20 cm D.21 cm
9.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的度数是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
10.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
(第7题图) (第8题图) (第10题图)
二、填空题
11.如图,若,被所截,则与 是内错角.
12.如图所示,若,则 ,根据是 .
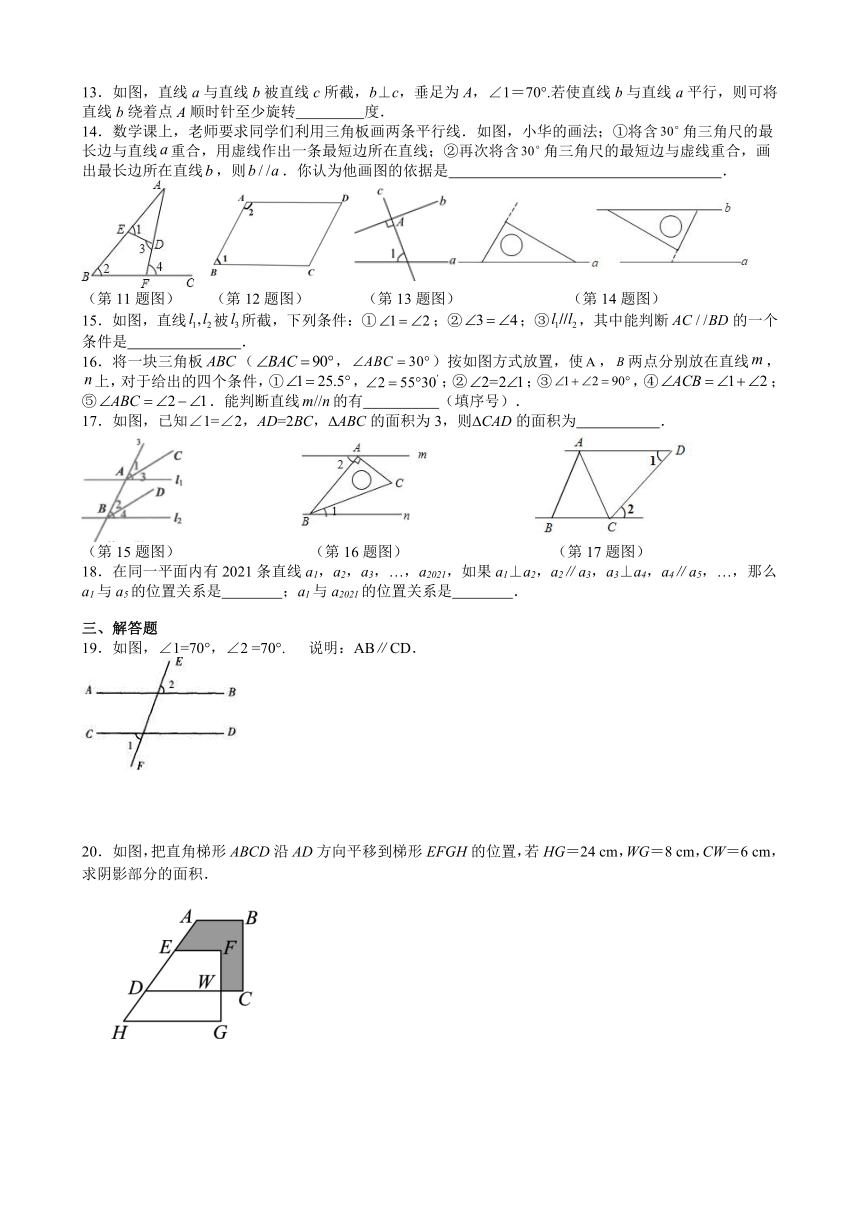
13.如图,直线a与直线b被直线c所截,b⊥c,垂足为A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针至少旋转 度.
14.数学课上,老师要求同学们利用三角板画两条平行线.如图,小华的画法;①将含角三角尺的最长边与直线重合,用虚线作出一条最短边所在直线;②再次将含角三角尺的最短边与虚线重合,画出最长边所在直线,则.你认为他画图的依据是 .
(第11题图) (第12题图) (第13题图) (第14题图)
15.如图,直线被所截,下列条件:①;②;③,其中能判断的一个条件是 .
16.将一块三角板(,)按如图方式放置,使,两点分别放在直线,上,对于给出的四个条件,①,;②;③,④;⑤.能判断直线的有 (填序号).
17.如图,已知∠1=∠2,AD=2BC, ABC的面积为3,则 CAD的面积为 .
(第15题图) (第16题图) (第17题图)
18.在同一平面内有2021条直线a1,a2,a3,…,a2021,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a5的位置关系是 ;a1与a2021的位置关系是 .
三、解答题
19.如图,∠1=70°,∠2 =70°. 说明:AB∥CD.
如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,若HG=24 cm,WG=8 cm,CW=6 cm,求阴影部分的面积.
21.如图,,平分.求证:.
22.如图,已知∠ABC=∠D,∠ABC+∠FCB=180°,求证:BE∥DG.
23.完成下面的证明:
如图,平分,平分,且,求证.
证明:∵平分(已知),
∴( ).
∵平分(已知),
∴ ( ).
∴( ).
∵(已知),
∴ ( ).
∴( ).
24.如图,一束光线在两面玻璃墙内进行传播,路径为A→B→C→D,根据光的反射性质,∠1=∠2,∠3=∠4,若∠2+∠3=90°,试探究直线AB与CD是否平行?并说明理由.
25.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
试卷第1页,共3页
参考答案:
1.C【解析】当∠1=∠3时,a∥b,∴∠3=∠1=55°,∵∠2+∠3=180°,∴∠2=125°,∴当∠2=125°时,a∥b,故选:C.
2.C【解析】A、正确,符合“内错角相等,两条直线平行”的判定定理;B、正确,符合“同位角相等,两条直线平行”的判定定理;C、错误,若∠3=∠4,则AD∥BE;D、正确,符合“同旁内角互补,两条直线平行”的判定定理;故选:C.
3.C【解析】A、∵∠1=∠4,∴AB∥CD,故本选项错误;B、∵∠2=∠3,∴BC∥AD,故本选项错误;
C、∵AD∥BC,∴∠BCD+∠ADC=180°,故本选项正确;D、∵∠1+∠2+∠C=180°,∴AB∥CD,故本选项错误;故选C.
4.B【解析】由图形可得:∠1与∠2是内错角,故A选项正确;∠1与∠4既不是同位角,也不是内错角,也不是同旁内角,故B选项错误;∠2与∠4是内错角,故C选项正确;∠2与∠3是同旁内角,故D选项正确,故选:B.
5.A【解析】①∵,∴,无法推出;②∵,∴;③∵,∴,无法推出;④∵,∴;
⑤∵∴,无法推出,综上所述,能判断的是:②④,有2个,故选:A.
6.B【解析】∵∠D=∠BCE,∴AD∥BC,故(1)能判定;∵∠B=∠BCE,∴AB∥DC,故(2)不能判定AD∥BC;∵∠A+∠B=180°,∴AD∥BC,故(3)能判定;∵∠A+∠D=180°,∴AB∥CD,故(4)不能判定;∵∠B=∠D,不能判定AD∥BC,故选:B.
7.C【解析】解:如图(2)当∠ACB'=42°时,∵,∴∠ACB'=∠A.∴CB'∥AB.
如图(2)当∠ACB'=138°时,∵∠A=42°,∴∴CB'∥AB.
综上可得,当或时,CB'∥AB.故选:C
8.C【解析】∵△ABE向右平移2cm得到△DCF,∴EF=AD=2cm,AE=DF.∵△ABE的周长为16cm,∴AB+BE+AE=16cm,∴四边形ABFD的周长=AB+BE+EF+DF+AD=AB+BE+AE+EF+AD=16+2+2=20cm,故答案为C.
9.D【解析】∵∠1+∠2=∠3+∠2=90,∴∠1=∠3,故①正确;∵,∴,∵∠E=60,∴∠1=∠E,∴AC∥DE,故②正确;∵,∴,∵,∴∠3=∠B,∴,故③正确;∵,∴∠CFE=∠C,∵∠CFE+∠E=∠C+∠1,∠1=∠E=,∴∠2=90-∠1=,故④正确,故选:D.
10.B【解析】如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,可以得到∠1=∠2.
因此,第一次与第二次拐的方向不相同,角度要相同,故只有B选项符合,故选B.
11.【解析】与是内错角,故答案为
12. AD BC 同旁内角互补,两直线平行
【解析】∵,∴,∴(同旁内角互补,两直线平行),
故答案为:AD;BC;同旁内角互补,两直线平行.
13.20【解析】如图:∵b⊥c,∴∠2=90°,∵∠1=70°,a∥b,∴直线b绕着点A顺时针旋转的度数=90°-70°=20°.
故答案为20.
14.内错角相等,两直线平行【解析】画图的依据是内错角,相等两直线平行.
故答案为:内错角相等,两直线平行
15.①【解析】∵,∴(同位角相等,两直线平行),而或均不能判定
故答案为:①.
16.①⑤【解析】①∵25.5°+∠ABC=55.5°=∠2=55°30',所以,m∥n;②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;③∠1+∠2=90°,不能判断直线m∥n;④∠ACB=∠1+∠2,不能判断直线m∥n;⑤∠ABC=∠2-∠1,判断直线m∥n;故答案为:①⑤.
17.6【解析】∵∠1=∠2,∴AD//BC,过点C作CM⊥AD,AN⊥BC,如图所示:∴CM=AN,∵,,,故答案为:6.
18.平行 ,平行【解析】如图,a1⊥a2,a2∥a3,∴a1⊥a3,∵a3⊥a4,∴a1∥a4,∵a4∥a5,∴a1∥a5,…,
依此类推,a1⊥a6,a1⊥a7,a1∥a8,a1∥a9,连续4条直线的位置关系为一个循环.∴2021=505×4+1,∴a1∥a2021.故答案是:平行,平行.
19.【解析】如图:∵∠1=70°,∴∠3=∠1=70°,又∵∠2 =70°,∴∠3=∠2=70°,∴ AB ∥CD.
20.【解析】∵由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=24cm,∴阴影部分的面积=梯形DWGH的面积,∵CW=6cm,∴DW=CD-CW=24-6=18cm,∴阴影部分的面积=(DW+HG)·WG=(18+24)×8=168cm2.
21.【解析】∵平分(已知),∴(角平分线定义).
又(已知),∴(等量代换).∴(内错角相等,两直线平行).
22.【解析】∵∠ABC=∠D,∠ABC+∠FCB=180°(已知),∴∠D+∠FCB=180°(等量代换),
∵∠ECD=∠FCB(对顶角相等),∴∠D+∠ECD=180°(等量代换),∴BE∥DG(同旁内角互补,两直线平行).
23.【解析】平分(已知),∴∠ABD=2∠α(角平分线的定义),平分(已知),∴2∠β(角平分线的定义),∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等式性质),(已知),∴∠ABD+∠BDC=180°(等量代换),∴(同旁内角互补,两直线平行).故答案为:角的平分线的定义;;角的平分线的定义;等式性质;;等量代换;同旁内角互补,两直线平行.
24.【解析】AB∥CD.理由:∵∠ABC=180°-∠1-∠2,∠BCD=180°-∠3-∠4,∠1=∠2,∠3=∠4,∴∠ABC=180°-2∠2,∠BCD=180°-2∠3,∴∠ABC+∠BCD=180°-2∠2+180°-2∠3=360°-2(∠2+∠3),∵∠2+∠3=90°,∴∠ABC+∠BCD=360°-2×90°=180°,∴AB∥CD
25.【解析】(1)∵AE⊥CE,∴∠AEC=90°,∴∠2+∠3=90°且∠1+∠4=90°,又∵EC平分∠DEF,∴∠3=∠4,∴∠1=∠2,∴EA平分∠BEF.
(2)∵AE⊥CE,∴∠AEC=90°,∴∠1+∠4=90°,∵∠1=∠A,∠4=∠C,∴∠B+∠D=180°-2∠1+180°-2∠4=360°-2(∠1+∠4)=180°,∴AB∥CD.
一、单选题
1.如图,直线a、b被直线c所截.若∠1=55°,则∠2的度数是( )时能判定a∥b.
A.35° B.45° C.125° D.145°
2.如图点E在BC的延长线上,则下列条件中,不能判定ABCD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
3.如图所示,下列推理正确的是 ( )
A.因为∠1=∠4,所以BC∥AD B.因为∠2=∠3,所以AB∥CD
C.因为AD∥BC,所以∠BCD+∠ADC=180° D.因为∠1+∠2+∠C=180°,所以BC∥AD
(第1题图) (第2题图) (第3题图)
4.如图,下列说法错误的是( ).
A.与是内错角 B.与是同位角 C.与是内错角 D.与是同旁内角
5.如图,下列四个结论:①∠1=∠3;②∠B=∠5;③∠B+∠BAD=180 ;④∠2=∠4;⑤∠D+∠BCD=180 .能判断AB∥CD的个数有 ( )
A.2个 B.3个 C.4个 D.5个
6.如图,在四边形ABCD中,点E在线段DC的延长线上,能使直线AD∥BC的条件有( )(1)∠D=∠BCE,(2)∠B=∠BCE,(3)∠A+∠B=180°,(4)∠A+∠D=180°,(5)∠B=∠D
A.1个 B.2个 C.3个 D.4个
(第4题图) (第5题图) (第6题图)
7.如图(1),在中,,边绕点按逆时针方向旋转一周回到原来的位置.在旋转的过程中(图(2)),当( )时,.
A.42° B.138° C.42°或138° D.42°或128°
8.如图,将△ABE向右平移2 cm得到△DCF,如果△ABE的周长是16 cm,那么四边形ABFD的周长是 ( )
A.16 cm B.18 cm C.20 cm D.21 cm
9.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的度数是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
10.将一副三角板按如图放置,则下列结论①;②如果,则有;③如果,则有;④如果,必有,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
(第7题图) (第8题图) (第10题图)
二、填空题
11.如图,若,被所截,则与 是内错角.
12.如图所示,若,则 ,根据是 .
13.如图,直线a与直线b被直线c所截,b⊥c,垂足为A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针至少旋转 度.
14.数学课上,老师要求同学们利用三角板画两条平行线.如图,小华的画法;①将含角三角尺的最长边与直线重合,用虚线作出一条最短边所在直线;②再次将含角三角尺的最短边与虚线重合,画出最长边所在直线,则.你认为他画图的依据是 .
(第11题图) (第12题图) (第13题图) (第14题图)
15.如图,直线被所截,下列条件:①;②;③,其中能判断的一个条件是 .
16.将一块三角板(,)按如图方式放置,使,两点分别放在直线,上,对于给出的四个条件,①,;②;③,④;⑤.能判断直线的有 (填序号).
17.如图,已知∠1=∠2,AD=2BC, ABC的面积为3,则 CAD的面积为 .
(第15题图) (第16题图) (第17题图)
18.在同一平面内有2021条直线a1,a2,a3,…,a2021,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a5的位置关系是 ;a1与a2021的位置关系是 .
三、解答题
19.如图,∠1=70°,∠2 =70°. 说明:AB∥CD.
如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,若HG=24 cm,WG=8 cm,CW=6 cm,求阴影部分的面积.
21.如图,,平分.求证:.
22.如图,已知∠ABC=∠D,∠ABC+∠FCB=180°,求证:BE∥DG.
23.完成下面的证明:
如图,平分,平分,且,求证.
证明:∵平分(已知),
∴( ).
∵平分(已知),
∴ ( ).
∴( ).
∵(已知),
∴ ( ).
∴( ).
24.如图,一束光线在两面玻璃墙内进行传播,路径为A→B→C→D,根据光的反射性质,∠1=∠2,∠3=∠4,若∠2+∠3=90°,试探究直线AB与CD是否平行?并说明理由.
25.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
试卷第1页,共3页
参考答案:
1.C【解析】当∠1=∠3时,a∥b,∴∠3=∠1=55°,∵∠2+∠3=180°,∴∠2=125°,∴当∠2=125°时,a∥b,故选:C.
2.C【解析】A、正确,符合“内错角相等,两条直线平行”的判定定理;B、正确,符合“同位角相等,两条直线平行”的判定定理;C、错误,若∠3=∠4,则AD∥BE;D、正确,符合“同旁内角互补,两条直线平行”的判定定理;故选:C.
3.C【解析】A、∵∠1=∠4,∴AB∥CD,故本选项错误;B、∵∠2=∠3,∴BC∥AD,故本选项错误;
C、∵AD∥BC,∴∠BCD+∠ADC=180°,故本选项正确;D、∵∠1+∠2+∠C=180°,∴AB∥CD,故本选项错误;故选C.
4.B【解析】由图形可得:∠1与∠2是内错角,故A选项正确;∠1与∠4既不是同位角,也不是内错角,也不是同旁内角,故B选项错误;∠2与∠4是内错角,故C选项正确;∠2与∠3是同旁内角,故D选项正确,故选:B.
5.A【解析】①∵,∴,无法推出;②∵,∴;③∵,∴,无法推出;④∵,∴;
⑤∵∴,无法推出,综上所述,能判断的是:②④,有2个,故选:A.
6.B【解析】∵∠D=∠BCE,∴AD∥BC,故(1)能判定;∵∠B=∠BCE,∴AB∥DC,故(2)不能判定AD∥BC;∵∠A+∠B=180°,∴AD∥BC,故(3)能判定;∵∠A+∠D=180°,∴AB∥CD,故(4)不能判定;∵∠B=∠D,不能判定AD∥BC,故选:B.
7.C【解析】解:如图(2)当∠ACB'=42°时,∵,∴∠ACB'=∠A.∴CB'∥AB.
如图(2)当∠ACB'=138°时,∵∠A=42°,∴∴CB'∥AB.
综上可得,当或时,CB'∥AB.故选:C
8.C【解析】∵△ABE向右平移2cm得到△DCF,∴EF=AD=2cm,AE=DF.∵△ABE的周长为16cm,∴AB+BE+AE=16cm,∴四边形ABFD的周长=AB+BE+EF+DF+AD=AB+BE+AE+EF+AD=16+2+2=20cm,故答案为C.
9.D【解析】∵∠1+∠2=∠3+∠2=90,∴∠1=∠3,故①正确;∵,∴,∵∠E=60,∴∠1=∠E,∴AC∥DE,故②正确;∵,∴,∵,∴∠3=∠B,∴,故③正确;∵,∴∠CFE=∠C,∵∠CFE+∠E=∠C+∠1,∠1=∠E=,∴∠2=90-∠1=,故④正确,故选:D.
10.B【解析】如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,可以得到∠1=∠2.
因此,第一次与第二次拐的方向不相同,角度要相同,故只有B选项符合,故选B.
11.【解析】与是内错角,故答案为
12. AD BC 同旁内角互补,两直线平行
【解析】∵,∴,∴(同旁内角互补,两直线平行),
故答案为:AD;BC;同旁内角互补,两直线平行.
13.20【解析】如图:∵b⊥c,∴∠2=90°,∵∠1=70°,a∥b,∴直线b绕着点A顺时针旋转的度数=90°-70°=20°.
故答案为20.
14.内错角相等,两直线平行【解析】画图的依据是内错角,相等两直线平行.
故答案为:内错角相等,两直线平行
15.①【解析】∵,∴(同位角相等,两直线平行),而或均不能判定
故答案为:①.
16.①⑤【解析】①∵25.5°+∠ABC=55.5°=∠2=55°30',所以,m∥n;②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;③∠1+∠2=90°,不能判断直线m∥n;④∠ACB=∠1+∠2,不能判断直线m∥n;⑤∠ABC=∠2-∠1,判断直线m∥n;故答案为:①⑤.
17.6【解析】∵∠1=∠2,∴AD//BC,过点C作CM⊥AD,AN⊥BC,如图所示:∴CM=AN,∵,,,故答案为:6.
18.平行 ,平行【解析】如图,a1⊥a2,a2∥a3,∴a1⊥a3,∵a3⊥a4,∴a1∥a4,∵a4∥a5,∴a1∥a5,…,
依此类推,a1⊥a6,a1⊥a7,a1∥a8,a1∥a9,连续4条直线的位置关系为一个循环.∴2021=505×4+1,∴a1∥a2021.故答案是:平行,平行.
19.【解析】如图:∵∠1=70°,∴∠3=∠1=70°,又∵∠2 =70°,∴∠3=∠2=70°,∴ AB ∥CD.
20.【解析】∵由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=24cm,∴阴影部分的面积=梯形DWGH的面积,∵CW=6cm,∴DW=CD-CW=24-6=18cm,∴阴影部分的面积=(DW+HG)·WG=(18+24)×8=168cm2.
21.【解析】∵平分(已知),∴(角平分线定义).
又(已知),∴(等量代换).∴(内错角相等,两直线平行).
22.【解析】∵∠ABC=∠D,∠ABC+∠FCB=180°(已知),∴∠D+∠FCB=180°(等量代换),
∵∠ECD=∠FCB(对顶角相等),∴∠D+∠ECD=180°(等量代换),∴BE∥DG(同旁内角互补,两直线平行).
23.【解析】平分(已知),∴∠ABD=2∠α(角平分线的定义),平分(已知),∴2∠β(角平分线的定义),∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等式性质),(已知),∴∠ABD+∠BDC=180°(等量代换),∴(同旁内角互补,两直线平行).故答案为:角的平分线的定义;;角的平分线的定义;等式性质;;等量代换;同旁内角互补,两直线平行.
24.【解析】AB∥CD.理由:∵∠ABC=180°-∠1-∠2,∠BCD=180°-∠3-∠4,∠1=∠2,∠3=∠4,∴∠ABC=180°-2∠2,∠BCD=180°-2∠3,∴∠ABC+∠BCD=180°-2∠2+180°-2∠3=360°-2(∠2+∠3),∵∠2+∠3=90°,∴∠ABC+∠BCD=360°-2×90°=180°,∴AB∥CD
25.【解析】(1)∵AE⊥CE,∴∠AEC=90°,∴∠2+∠3=90°且∠1+∠4=90°,又∵EC平分∠DEF,∴∠3=∠4,∴∠1=∠2,∴EA平分∠BEF.
(2)∵AE⊥CE,∴∠AEC=90°,∴∠1+∠4=90°,∵∠1=∠A,∠4=∠C,∴∠B+∠D=180°-2∠1+180°-2∠4=360°-2(∠1+∠4)=180°,∴AB∥CD.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
