2021—2022学年人教版八年级数学下册18.1.2平行四边形的判定课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.1.2平行四边形的判定课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 276.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 17:00:52 | ||
图片预览


文档简介
18.1.2 平行四边形的判定课后练习
一、选择题
1.下列条件不能判定四边形是平行四边形的是( ).A., B.,
C., D.,
2.已知A,B,C三点的坐标分别是(3,3),(8,3),(4,6),若以A,B,C,D四点为顶点的四边形是平行四边形,则D点的坐标不可能是( )
A.(,6) B.(9,6) C.(7,0) D.(0,)
3.给定不在同一直线上的三点,则以这三点为顶点的平行四边形有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在四边形中,AB∥CD,添加下列一个条件后,一定能判定四边形是平行四边形的是( )
A. B. C. D.
5.如图,在△ABC中,点D、E、F分别是各边的中点,若△ABC的面积为16cm2,则△DEF的面积是( )cm2.
A.2 B.4 C.6 D.8
6.已知:如图,点A(,0),B(,0),将线段AB平移后得到线段CD,点A的对应点C恰好落在y轴上,且四边形ABDC的面积为9,则四边形ABDC的周长是( )
A.14 B.16 C.18 D.20
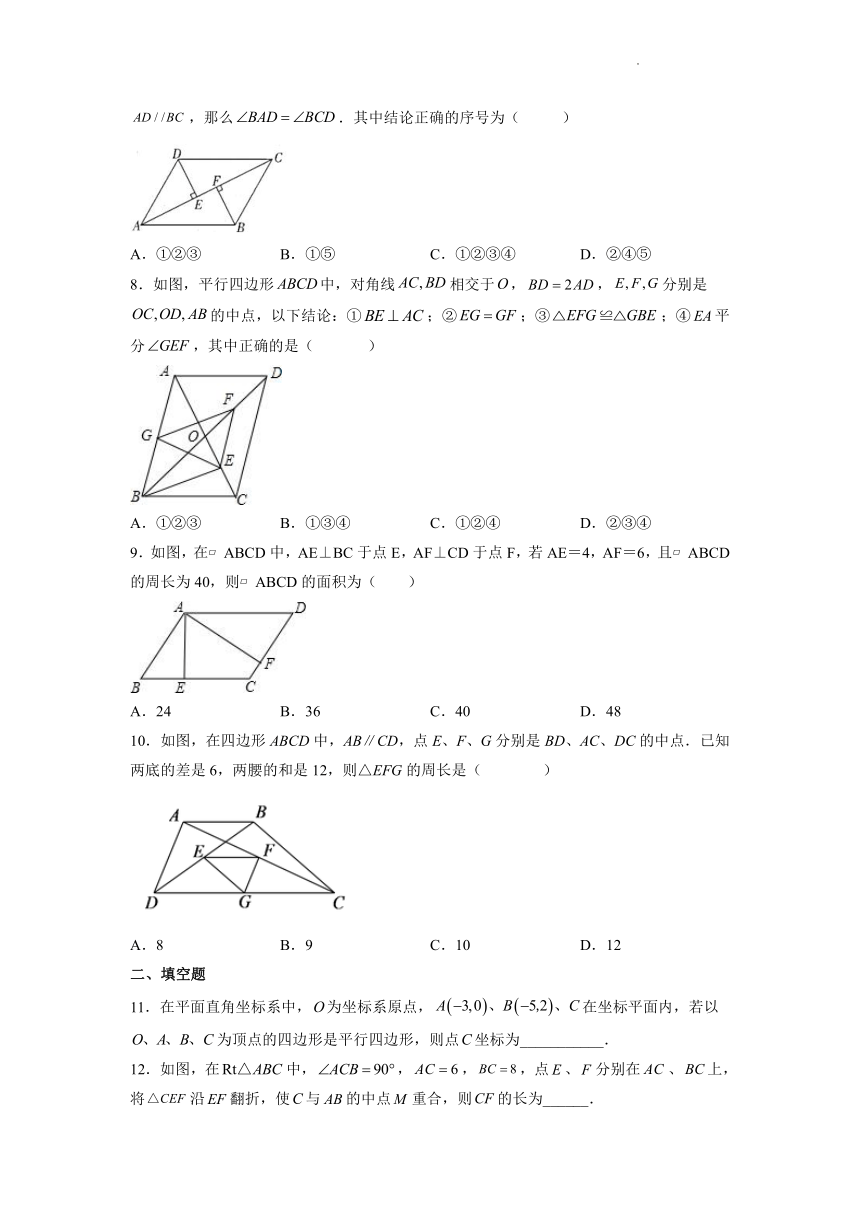
7.如图,,于点,于点,关于下列结论:①;②;③点到的距离是线段;④;⑤如果,那么.其中结论正确的序号为( )
A.①②③ B.①⑤ C.①②③④ D.②④⑤
8.如图,平行四边形中,对角线相交于,,分别是的中点,以下结论:①;②;③;④平分,其中正确的是( )
A.①②③ B.①③④ C.①②④ D.②③④
9.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
10.如图,在四边形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底的差是6,两腰的和是12,则△EFG的周长是( )
A.8 B.9 C.10 D.12
二、填空题
11.在平面直角坐标系中,为坐标系原点,在坐标平面内,若以为顶点的四边形是平行四边形,则点坐标为___________.
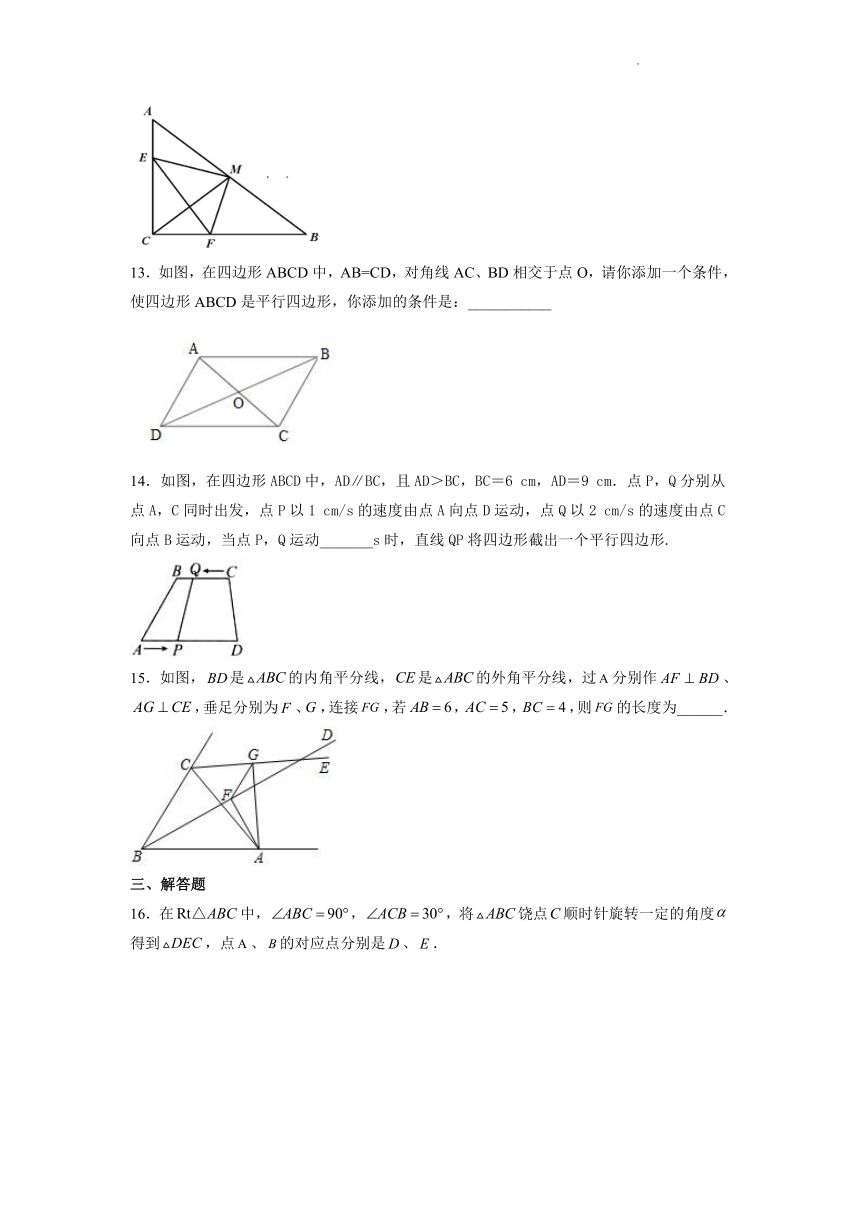
12.如图,在中,,,,点、分别在、上,将沿翻折,使与的中点重合,则的长为______.
13.如图,在四边形ABCD中,AB=CD,对角线AC、BD相交于点O,请你添加一个条件,使四边形ABCD是平行四边形,你添加的条件是:___________
14.如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,AD=9 cm.点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动,当点P,Q运动_______s时,直线QP将四边形截出一个平行四边形.
15.如图,是的内角平分线,是的外角平分线,过分别作、,垂足分别为、,连接,若,,,则的长度为______.
三、解答题
16.在中,,,将饶点顺时针旋转一定的角度得到,点、的对应点分别是、.
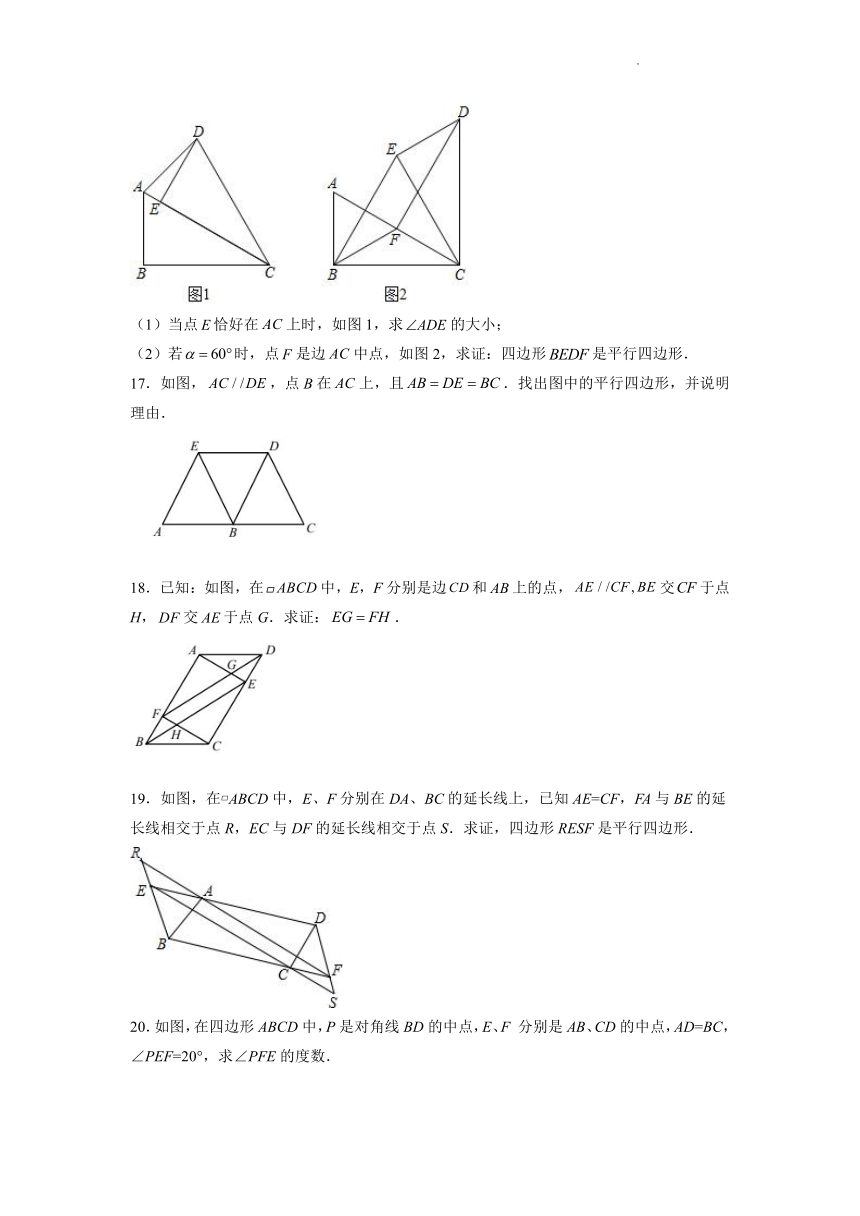
(1)当点恰好在上时,如图1,求的大小;
(2)若时,点是边中点,如图2,求证:四边形是平行四边形.
17.如图,,点B在上,且.找出图中的平行四边形,并说明理由.
18.已知:如图,在中,E,F分别是边和上的点,交于点H,交于点G.求证:.
19.如图,在 ABCD中,E、F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S.求证,四边形RESF是平行四边形.
20.如图,在四边形ABCD中,P是对角线BD的中点,E、F 分别是AB、CD的中点,AD=BC,∠PEF=20°,求∠PFE的度数.
21.如图,已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,求证:BD=2EF.
22.如图,点在外,连接,,,并延长交于点,恰好为的中点.
(1)求证:;
(2)若,,,,求的长.
23.如图,在中,点是边的中点,点在内,平分,,点在边上,.
(1)若的面积为4,则四边形的面积为
(2)求证:四边形是平行四边形.
(3)判断线段、、之间具有怎样的数量关系?并证明你所得到的结论.
【参考答案】
1.C 2.D 3.C 4.C 5.B 6.B 7.B 8.C 9.D 10.D
11.或或.
12.
13.AD=BC(答案不唯一)
14.2或3
15.
16.解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴∠ACB=∠DCE=30°,∠DEA=∠ABC=90°,
∵CA=CD,
∴∠ADC=∠DAC= (180° 30°)=75°,
∴∠ADE=90°-75°=15°;
(2)证明:如图2,∵点F是边AC中点,
∴CF=AC,
∵∠BAC=30°,
∴AB=AC,
∴CF=AB,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BCE=60°,BC=EC,
∴△BEC为等边三角形,
∴BE=BC=EC,
在△CFD和△CBA中,
∴DF⊥AC,易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,而BF=DE,
∴四边形BEDF是平行四边形.
17.
解:∵,
∴,,
∵,
∴且,
且,
∴四边形ABDE是平行四边形,四边形BCDE是平行四边形.
18.
证明:四边形是平行四边形,
,
,
四边形是平行四边形,
,,
,
即,
,
四边形是平行四边形,
,
,
四边形是平行四边形,
.
19
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BR∥DS,
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥EC,
∴四边形RESF是平行四边形.
20.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=20°.
21.证明:∵AD=AC,AE⊥CD
∴CE=ED
∵F是BC的中点
∴EF是△CDB的中位线
∴BD=2EF
22.解:(1)证明:如图,连接交于点,
∵四边形是平行四边形,
∴BO=OD,
是的中点,
又∵F为的中点,
是的中位线,
,即;
(2)∵四边形是平行四边形,
,
,
,
,,,
,
,,
,
.
23.(1)解:延长CE交AB于点G,如图所示:
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
∵AE平分∠BAC,
∴∠GAE=∠CAE,
在△AEG和△AEC中,
,
∴△AEG≌△AEC(ASA),
∴EG=EC,
∵点D是边BC的中点,
∴DE为△BCG的中位线,BD=CD,
∴DE∥AB,
又∵EF∥BC,
∴四边形BDEF是平行四边形,且与△DEC等底等高,
∴平行四边形BDEF的面积=2△DEC的面积=2×4=8,
故答案为:8;
(2)证明:由(1)得:△AEG≌△AEC(ASA),
∴EG=EC,
∵点D是边BC的中点,
∴DE为△BCG的中位线,
∴DE∥AB,
又∵EF∥BC,
∴四边形BDEF是平行四边形;
(3)解:BF=(AB AC),证明如下:
由(2)得:四边形BDEF是平行四边形,DE为△BCG的中位线,
∴BF=DE,DE=BG,
∴BF=BG,
由(1)得:△AEG≌△AEC,
∴AG=AC,
∴BF=(AB AG)=(AB AC).
即AB-AC=2BF
一、选择题
1.下列条件不能判定四边形是平行四边形的是( ).A., B.,
C., D.,
2.已知A,B,C三点的坐标分别是(3,3),(8,3),(4,6),若以A,B,C,D四点为顶点的四边形是平行四边形,则D点的坐标不可能是( )
A.(,6) B.(9,6) C.(7,0) D.(0,)
3.给定不在同一直线上的三点,则以这三点为顶点的平行四边形有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在四边形中,AB∥CD,添加下列一个条件后,一定能判定四边形是平行四边形的是( )
A. B. C. D.
5.如图,在△ABC中,点D、E、F分别是各边的中点,若△ABC的面积为16cm2,则△DEF的面积是( )cm2.
A.2 B.4 C.6 D.8
6.已知:如图,点A(,0),B(,0),将线段AB平移后得到线段CD,点A的对应点C恰好落在y轴上,且四边形ABDC的面积为9,则四边形ABDC的周长是( )
A.14 B.16 C.18 D.20
7.如图,,于点,于点,关于下列结论:①;②;③点到的距离是线段;④;⑤如果,那么.其中结论正确的序号为( )
A.①②③ B.①⑤ C.①②③④ D.②④⑤
8.如图,平行四边形中,对角线相交于,,分别是的中点,以下结论:①;②;③;④平分,其中正确的是( )
A.①②③ B.①③④ C.①②④ D.②③④
9.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
10.如图,在四边形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底的差是6,两腰的和是12,则△EFG的周长是( )
A.8 B.9 C.10 D.12
二、填空题
11.在平面直角坐标系中,为坐标系原点,在坐标平面内,若以为顶点的四边形是平行四边形,则点坐标为___________.
12.如图,在中,,,,点、分别在、上,将沿翻折,使与的中点重合,则的长为______.
13.如图,在四边形ABCD中,AB=CD,对角线AC、BD相交于点O,请你添加一个条件,使四边形ABCD是平行四边形,你添加的条件是:___________
14.如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,AD=9 cm.点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动,当点P,Q运动_______s时,直线QP将四边形截出一个平行四边形.
15.如图,是的内角平分线,是的外角平分线,过分别作、,垂足分别为、,连接,若,,,则的长度为______.
三、解答题
16.在中,,,将饶点顺时针旋转一定的角度得到,点、的对应点分别是、.
(1)当点恰好在上时,如图1,求的大小;
(2)若时,点是边中点,如图2,求证:四边形是平行四边形.
17.如图,,点B在上,且.找出图中的平行四边形,并说明理由.
18.已知:如图,在中,E,F分别是边和上的点,交于点H,交于点G.求证:.
19.如图,在 ABCD中,E、F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S.求证,四边形RESF是平行四边形.
20.如图,在四边形ABCD中,P是对角线BD的中点,E、F 分别是AB、CD的中点,AD=BC,∠PEF=20°,求∠PFE的度数.
21.如图,已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,求证:BD=2EF.
22.如图,点在外,连接,,,并延长交于点,恰好为的中点.
(1)求证:;
(2)若,,,,求的长.
23.如图,在中,点是边的中点,点在内,平分,,点在边上,.
(1)若的面积为4,则四边形的面积为
(2)求证:四边形是平行四边形.
(3)判断线段、、之间具有怎样的数量关系?并证明你所得到的结论.
【参考答案】
1.C 2.D 3.C 4.C 5.B 6.B 7.B 8.C 9.D 10.D
11.或或.
12.
13.AD=BC(答案不唯一)
14.2或3
15.
16.解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴∠ACB=∠DCE=30°,∠DEA=∠ABC=90°,
∵CA=CD,
∴∠ADC=∠DAC= (180° 30°)=75°,
∴∠ADE=90°-75°=15°;
(2)证明:如图2,∵点F是边AC中点,
∴CF=AC,
∵∠BAC=30°,
∴AB=AC,
∴CF=AB,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BCE=60°,BC=EC,
∴△BEC为等边三角形,
∴BE=BC=EC,
在△CFD和△CBA中,
∴DF⊥AC,易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,而BF=DE,
∴四边形BEDF是平行四边形.
17.
解:∵,
∴,,
∵,
∴且,
且,
∴四边形ABDE是平行四边形,四边形BCDE是平行四边形.
18.
证明:四边形是平行四边形,
,
,
四边形是平行四边形,
,,
,
即,
,
四边形是平行四边形,
,
,
四边形是平行四边形,
.
19
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BR∥DS,
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥EC,
∴四边形RESF是平行四边形.
20.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=20°.
21.证明:∵AD=AC,AE⊥CD
∴CE=ED
∵F是BC的中点
∴EF是△CDB的中位线
∴BD=2EF
22.解:(1)证明:如图,连接交于点,
∵四边形是平行四边形,
∴BO=OD,
是的中点,
又∵F为的中点,
是的中位线,
,即;
(2)∵四边形是平行四边形,
,
,
,
,,,
,
,,
,
.
23.(1)解:延长CE交AB于点G,如图所示:
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
∵AE平分∠BAC,
∴∠GAE=∠CAE,
在△AEG和△AEC中,
,
∴△AEG≌△AEC(ASA),
∴EG=EC,
∵点D是边BC的中点,
∴DE为△BCG的中位线,BD=CD,
∴DE∥AB,
又∵EF∥BC,
∴四边形BDEF是平行四边形,且与△DEC等底等高,
∴平行四边形BDEF的面积=2△DEC的面积=2×4=8,
故答案为:8;
(2)证明:由(1)得:△AEG≌△AEC(ASA),
∴EG=EC,
∵点D是边BC的中点,
∴DE为△BCG的中位线,
∴DE∥AB,
又∵EF∥BC,
∴四边形BDEF是平行四边形;
(3)解:BF=(AB AC),证明如下:
由(2)得:四边形BDEF是平行四边形,DE为△BCG的中位线,
∴BF=DE,DE=BG,
∴BF=BG,
由(1)得:△AEG≌△AEC,
∴AG=AC,
∴BF=(AB AG)=(AB AC).
即AB-AC=2BF
