北京课改版 八年级下册数学 15.4.2 菱形的判定 课件(共18张PPT)
文档属性
| 名称 | 北京课改版 八年级下册数学 15.4.2 菱形的判定 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 612.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
菱形的判定
复习与回顾:
1.菱形的定义:
2.菱形的性质(不同于一般的平行四边形):
有一组邻边相等的平行四边形叫做菱形.
(1)菱形的四条边都相等;
(2)菱形的对角线互相垂直,并且每一条对角线平分一组对角.
(a,b为菱形的对角线的长)
3.菱形的面积公式:
学习目标
1.理解并掌握菱形的判定方法.
2.学会运用菱形的判定方法解决一些简单的问题;进一步发展合情推理能力;逐步掌握说理的基本方法。
3.经历探索菱形判定方法的过程,发展主动探索、研究的习惯。
根据菱形的定义,可得菱形的第一个判定的方法
∵四边形ABCD是平行四边形,且AB=AD
∴四边形ABCD是菱形
符号语言:
有一组邻边相等的平行四边形叫做菱形
还有其他么方法吗
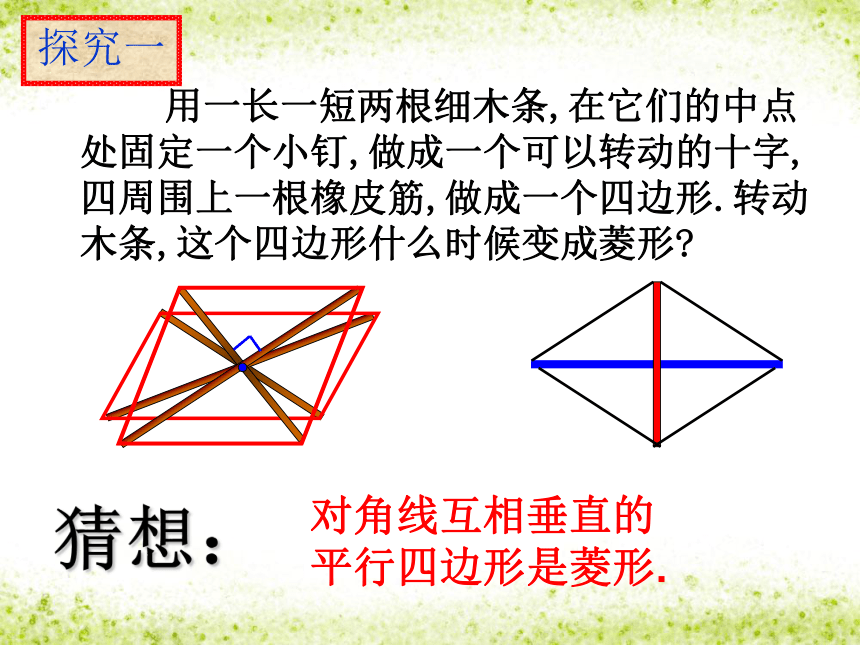
探究一
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想:
对角线互相垂直的平行四边形是菱形.
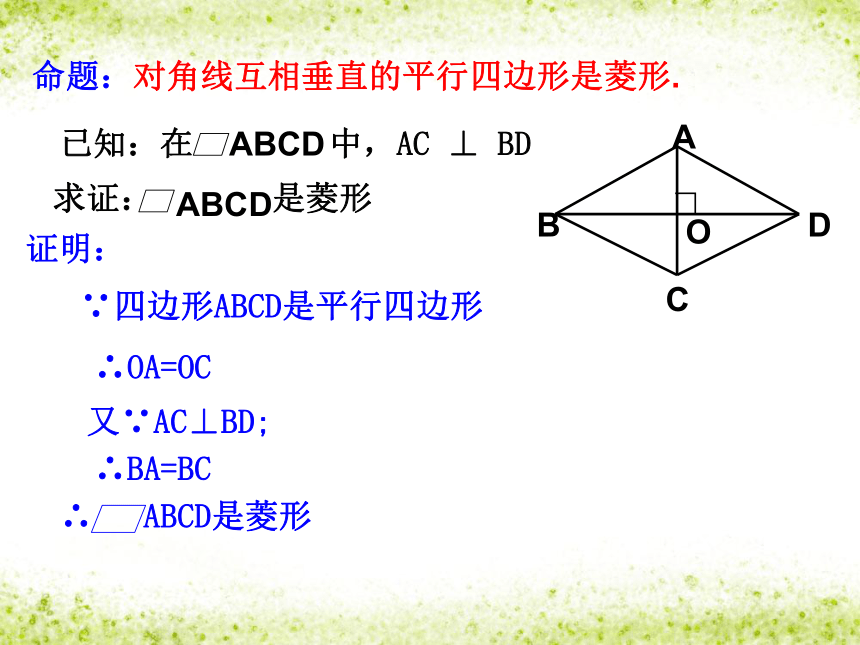
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴ ABCD是菱形
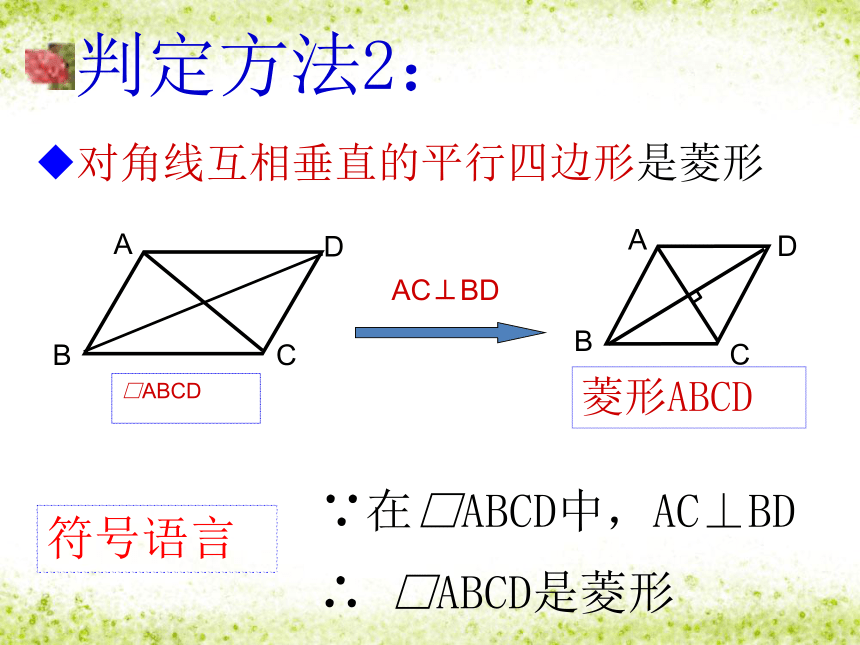
判定方法2:
对角线互相垂直的平行四边形是菱形
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
符号语言
先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?说出你的理由
猜想:有四条边相等的四边形是菱形。
A
B
C
D
O
探究二
命题:有四条边相等的四边形是菱形.
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
四条边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵在四边形ABCD中AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
判定方法3:
符号语言
1、下列三个图形是不是菱形,为什么
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形
3
3
4
4
┍
2、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形; ( )
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形. ( )
╳
√
╳
╳
3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
矩
菱
矩
菱
(1)下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
(2)下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
C
4、选择:
1.如图, ABCD的两条对角线AC、BD相交于点O,AB= 5 ,AC=8,DB=6.
求证:四边形ABCD是菱形.
A
B
C
D
O
勇攀高峰
勇攀高峰
2.已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F 求证:四边形AFCE是菱形。
一组邻边相等
对角线互相垂直
四条边相等
四边形
平行四边形
菱形
小结:
作业
《课时作业》第33-34页
菱形的判定
复习与回顾:
1.菱形的定义:
2.菱形的性质(不同于一般的平行四边形):
有一组邻边相等的平行四边形叫做菱形.
(1)菱形的四条边都相等;
(2)菱形的对角线互相垂直,并且每一条对角线平分一组对角.
(a,b为菱形的对角线的长)
3.菱形的面积公式:
学习目标
1.理解并掌握菱形的判定方法.
2.学会运用菱形的判定方法解决一些简单的问题;进一步发展合情推理能力;逐步掌握说理的基本方法。
3.经历探索菱形判定方法的过程,发展主动探索、研究的习惯。
根据菱形的定义,可得菱形的第一个判定的方法
∵四边形ABCD是平行四边形,且AB=AD
∴四边形ABCD是菱形
符号语言:
有一组邻边相等的平行四边形叫做菱形
还有其他么方法吗
探究一
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想:
对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴ ABCD是菱形
判定方法2:
对角线互相垂直的平行四边形是菱形
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
符号语言
先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?说出你的理由
猜想:有四条边相等的四边形是菱形。
A
B
C
D
O
探究二
命题:有四条边相等的四边形是菱形.
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
四条边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵在四边形ABCD中AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
判定方法3:
符号语言
1、下列三个图形是不是菱形,为什么
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形
3
3
4
4
┍
2、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形; ( )
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形. ( )
╳
√
╳
╳
3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
矩
菱
矩
菱
(1)下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
(2)下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
C
4、选择:
1.如图, ABCD的两条对角线AC、BD相交于点O,AB= 5 ,AC=8,DB=6.
求证:四边形ABCD是菱形.
A
B
C
D
O
勇攀高峰
勇攀高峰
2.已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F 求证:四边形AFCE是菱形。
一组邻边相等
对角线互相垂直
四条边相等
四边形
平行四边形
菱形
小结:
作业
《课时作业》第33-34页
同课章节目录
