人教八下数学18.1.1平行四边形的性质 教学设计 (表格式)
文档属性
| 名称 | 人教八下数学18.1.1平行四边形的性质 教学设计 (表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 66.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 10:41:22 | ||
图片预览

文档简介
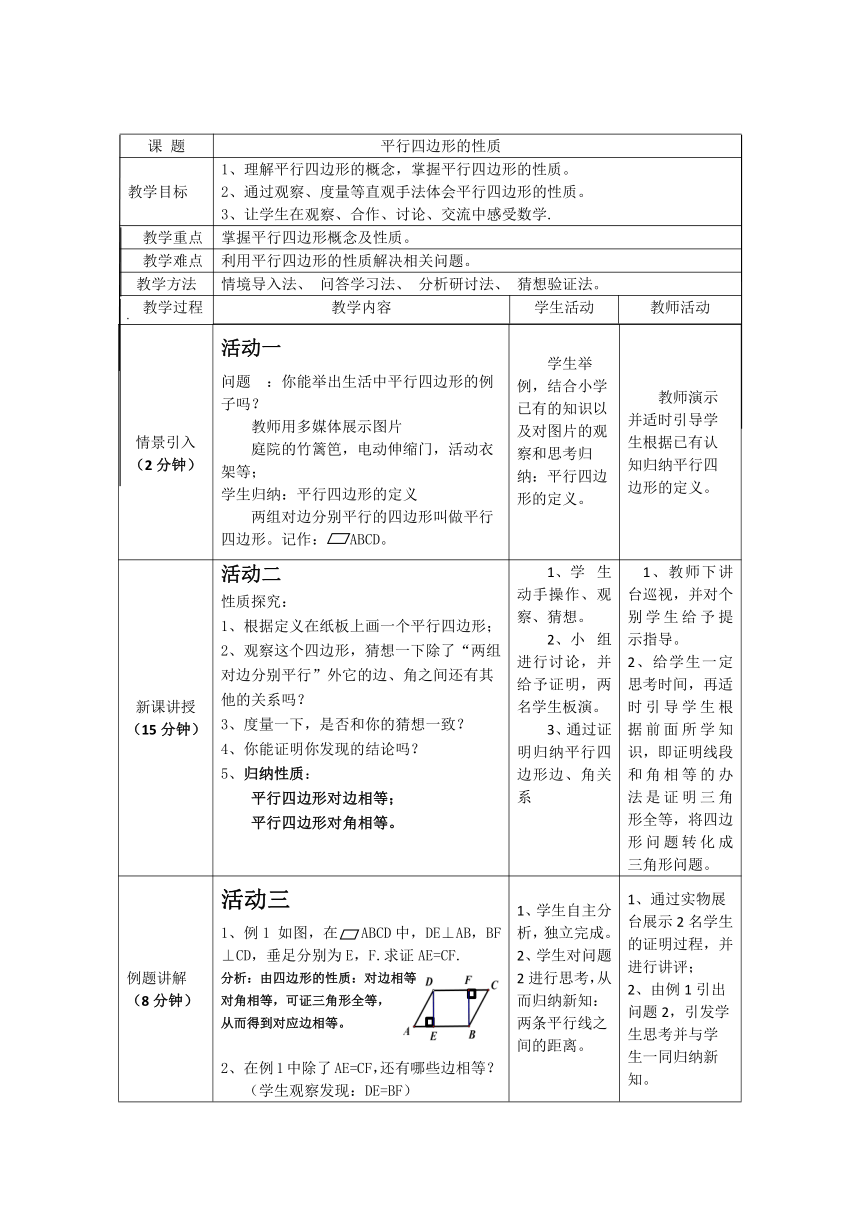
课 题 平行四边形的性质
教学目标 1、理解平行四边形的概念,掌握平行四边形的性质。 2、通过观察、度量等直观手法体会平行四边形的性质。 3、让学生在观察、合作、讨论、交流中感受数学.
教学重点 掌握平行四边形概念及性质。
教学难点 利用平行四边形的性质解决相关问题。
教学方法 情境导入法、 问答学习法、 分析研讨法、 猜想验证法。
教学过程 教学内容 学生活动 教师活动
情景引入(2分钟) 活动一问题 :你能举出生活中平行四边形的例子吗?教师用多媒体展示图片 庭院的竹篱笆,电动伸缩门,活动衣架等;学生归纳:平行四边形的定义 两组对边分别平行的四边形叫做平行四边形。记作: ABCD。 学生举例,结合小学已有的知识以及对图片的观察和思考归纳:平行四边形的定义。 教师演示并适时引导学生根据已有认知归纳平行四边形的定义。
新课讲授(15分钟) 活动二性质探究: 根据定义在纸板上画一个平行四边形;观察这个四边形,猜想一下除了“两组对边分别平行”外它的边、角之间还有其他的关系吗?度量一下,是否和你的猜想一致? 你能证明你发现的结论吗?归纳性质:平行四边形对边相等;平行四边形对角相等。 学生动手操作、观察、猜想。小组进行讨论,并给予证明,两名学生板演。3、通过证明归纳平行四边形边、角关系 1、教师下讲台巡视,并对个别学生给予提示指导。2、给学生一定思考时间,再适时引导学生根据前面所学知识,即证明线段和角相等的办法是证明三角形全等,将四边形问题转化成三角形问题。
例题讲解(8分钟) 活动三1、例1 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证AE=CF.分析:由四边形的性质:对边相等对角相等,可证三角形全等,从而得到对应边相等。在例1中除了AE=CF,还有哪些边相等? (学生观察发现:DE=BF)在CD边上任意找一点,过这一点做AB的垂线,则垂线是否和DE、BF相等?结论:1、两条平行线之间的任何两条平行线段都相等。 2、一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离。 1、学生自主分析,独立完成。2、学生对问题2进行思考,从而归纳新知:两条平行线之间的距离。思考并归纳总结出两平行线之间的距离。 通过实物展台展示2名学生的证明过程,并进行讲评;由例1引出问题2,引发学生思考并与学生一同归纳新知。
习题巩固(13分钟) 练习1、(1)在 ABCD中,已知∠A=130°,则∠B=__ , ∠C=___ ,∠D=__.
(2)在 ABCD中,AB=3,BC=5,则它的周长是_______.练习2:在 ABCD中 (1)若∠A:∠B=1:2,则∠A=____,∠B=____,∠D=____; (2)若∠A+∠C=90°,则∠D=____.练习3:在 ABCD中,已知AB=4,BC=6,∠B=60°,则AD与BC之间的距离为_____.练习4:已知直线a∥b,BC=4,若△ABC的面积为6,则直线a,b之间的距离是_______. 1、练习1、2学生快速口答,并说出解题思路;2、练习3、4学生独立完成并上台板演,其他学生作修改和补充。 教师下讲台巡视,并对个别学生给予提示指导。
课堂小结(2分钟) 这节课你学到了什么?还有什么疑惑吗? 1、性质: 平行四边形的对边相等 平行四边形的对角相等2、两条平行线之间的距离 两条平行线中,一条直线上任意一点到另一条直线的距离。 学生回忆本节课所学内容,并总结归纳。 教师引导学生回忆、总结。
作业布置 教科书P49 第1题、第2题 同步练习册 课后再次巩固
板书设计 18.1.1 平行四边形的性质 平行四边形定义:两组对边分别平行的四边形.性质: 例1 练习
在 ABCD中
∠A=∠C,∠B=∠D
在 ABCD中
AB=CD,AD=BC
教学目标 1、理解平行四边形的概念,掌握平行四边形的性质。 2、通过观察、度量等直观手法体会平行四边形的性质。 3、让学生在观察、合作、讨论、交流中感受数学.
教学重点 掌握平行四边形概念及性质。
教学难点 利用平行四边形的性质解决相关问题。
教学方法 情境导入法、 问答学习法、 分析研讨法、 猜想验证法。
教学过程 教学内容 学生活动 教师活动
情景引入(2分钟) 活动一问题 :你能举出生活中平行四边形的例子吗?教师用多媒体展示图片 庭院的竹篱笆,电动伸缩门,活动衣架等;学生归纳:平行四边形的定义 两组对边分别平行的四边形叫做平行四边形。记作: ABCD。 学生举例,结合小学已有的知识以及对图片的观察和思考归纳:平行四边形的定义。 教师演示并适时引导学生根据已有认知归纳平行四边形的定义。
新课讲授(15分钟) 活动二性质探究: 根据定义在纸板上画一个平行四边形;观察这个四边形,猜想一下除了“两组对边分别平行”外它的边、角之间还有其他的关系吗?度量一下,是否和你的猜想一致? 你能证明你发现的结论吗?归纳性质:平行四边形对边相等;平行四边形对角相等。 学生动手操作、观察、猜想。小组进行讨论,并给予证明,两名学生板演。3、通过证明归纳平行四边形边、角关系 1、教师下讲台巡视,并对个别学生给予提示指导。2、给学生一定思考时间,再适时引导学生根据前面所学知识,即证明线段和角相等的办法是证明三角形全等,将四边形问题转化成三角形问题。
例题讲解(8分钟) 活动三1、例1 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证AE=CF.分析:由四边形的性质:对边相等对角相等,可证三角形全等,从而得到对应边相等。在例1中除了AE=CF,还有哪些边相等? (学生观察发现:DE=BF)在CD边上任意找一点,过这一点做AB的垂线,则垂线是否和DE、BF相等?结论:1、两条平行线之间的任何两条平行线段都相等。 2、一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离。 1、学生自主分析,独立完成。2、学生对问题2进行思考,从而归纳新知:两条平行线之间的距离。思考并归纳总结出两平行线之间的距离。 通过实物展台展示2名学生的证明过程,并进行讲评;由例1引出问题2,引发学生思考并与学生一同归纳新知。
习题巩固(13分钟) 练习1、(1)在 ABCD中,已知∠A=130°,则∠B=__ , ∠C=___ ,∠D=__.
(2)在 ABCD中,AB=3,BC=5,则它的周长是_______.练习2:在 ABCD中 (1)若∠A:∠B=1:2,则∠A=____,∠B=____,∠D=____; (2)若∠A+∠C=90°,则∠D=____.练习3:在 ABCD中,已知AB=4,BC=6,∠B=60°,则AD与BC之间的距离为_____.练习4:已知直线a∥b,BC=4,若△ABC的面积为6,则直线a,b之间的距离是_______. 1、练习1、2学生快速口答,并说出解题思路;2、练习3、4学生独立完成并上台板演,其他学生作修改和补充。 教师下讲台巡视,并对个别学生给予提示指导。
课堂小结(2分钟) 这节课你学到了什么?还有什么疑惑吗? 1、性质: 平行四边形的对边相等 平行四边形的对角相等2、两条平行线之间的距离 两条平行线中,一条直线上任意一点到另一条直线的距离。 学生回忆本节课所学内容,并总结归纳。 教师引导学生回忆、总结。
作业布置 教科书P49 第1题、第2题 同步练习册 课后再次巩固
板书设计 18.1.1 平行四边形的性质 平行四边形定义:两组对边分别平行的四边形.性质: 例1 练习
在 ABCD中
∠A=∠C,∠B=∠D
在 ABCD中
AB=CD,AD=BC
